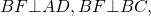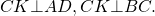Докажите что трапеция равнобедренная если углы при каждом основании равны
Если у трапеции углы при основании равны
(I признак равнобедренной трапеции).
Если у трапеции углы при основании равны, то она — равнобедренная.

Доказать: ABCD — равнобедренная.
1) Проведем высоты трапеции BF и CK:
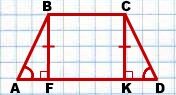
∠AFB=90º, ∠DKC=90º (так как BF и CK — высоты трапеции).
BF=CK (как высоты трапеции).
Следовательно, треугольники ABF и DCK равны (по катету и острому углу).
3) Из равенства треугольников следует равенство соответствующих сторон: AB=CD.
Следовательно, трапеция ABCD — равнобедренная ( по определению).
∠A+∠B=180º (как внутренние односторонние при AD ∥ BC и секущей AB),
∠D+∠C =180º (как внутренние односторонние при AD ∥ BC и секущей CD).
Таким образом, из равенства углов при меньшем основании следует равенство углов и при большем основании трапеции. Уже доказали, что в этом случае трапеция — равнобедренная.