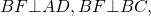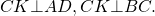Докажите что трапеция равнобедренная если углы при основании равны 8 класс

Если у трапеции углы при основании равны

(I признак равнобедренной трапеции).

Если у трапеции углы при основании равны, то она — равнобедренная.

Дано : ABCD — трапеция,

Доказать: ABCD — равнобедренная.

1) Проведем высоты трапеции BF и CK:

2) Рассмотрим треугольники ABF и DCK.

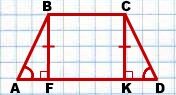
∠AFB=90º, ∠DKC=90º (так как BF и CK — высоты трапеции).

BF=CK (как высоты трапеции).

Следовательно, треугольники ABF и DCK равны (по катету и острому углу).

3) Из равенства треугольников следует равенство соответствующих сторон: AB=CD.

Следовательно, трапеция ABCD — равнобедренная ( по определению).

∠A+∠B=180º (как внутренние односторонние при AD ∥ BC и секущей AB),

∠D+∠C =180º (как внутренние односторонние при AD ∥ BC и секущей CD).

Таким образом, из равенства углов при меньшем основании следует равенство углов и при большем основании трапеции. Уже доказали, что в этом случае трапеция — равнобедренная.

Источник

Геометрия. 8 класс

Четырёхугольник, две стороны которого параллельны, а две другие не параллельны, называется трапецией. Параллельные стороны называются основаниями трапеции, непараллельные стороны – боковыми сторонами.
Если один из углов трапеции прямой, то она называется прямоугольной. Если боковые стороны трапеции равны, то она называется равнобедренной трапецией (равнобокой).
Сформулируем и докажем свойства равнобедренной трапеции:
Свойство первое: в равнобедренной трапеции углы при каждом основании равны.
Для доказательства проведём отрезок CK, параллельный AB.

CK || AB, ABCK – параллелограмм (стороны попарно параллельны), значит AB = CK, но AB = CD (трапеция равнобедренная), значит CK = CD, треугольник KCD – равнобедренный,
По свойству равнобедренного треугольника ∠1 = ∠2.

∠2 = ∠3 (соответственные при секущей AD и параллельных AB и CK). Следовательно, ∠1 = ∠3.
ABC = 180° − ∠3 = 180° − ∠1 = ∠BCD.
Второе свойство равнобедренной трапеции: диагонали равнобедренной трапеции равны.
Дано: ABCD – равнобедренная трапеция, BC || AD
Доказать: AC = BD.

Для доказательства рассмотрим треугольники ABC и DCB. Треугольники ABC и DCB равны (AB = CD, BC – общая сторона, ∠ABC = ∠DCA). Следовательно, AC = BD.
Теоремы, обратные свойствам равнобедренной трапеции, также верны. Это признаки равнобедренной трапеции.
Признак первый: если углы при основании трапеции равны, то трапеция является равнобедренной.
Дано: ABCD – трапеция, BC || AD
∠BAC = ∠CDA
Доказать: ABCD – равнобедренная трапеция

Для доказательства проведем отрезок CK, параллельный AB.
Доказательство:
CK || AB, следовательно ABCK – параллелограмм, тогда AB = CK, ∠A = ∠CKD.
Получится равнобедренный треугольник CKD (∠A = ∠CKD и ∠A = ∠CDA), поэтому
CK = CD и AB = CK = CD. Следовательно, ABCD – равнобедренная трапеция.
Второй признак: если диагонали трапеции равны, то трапеция равнобедренная.
Дано: ABCD –трапеция, BC || AD
AC = BD
Доказать: ABCD – равнобедренная трапеция

Источник

«Трапеция». 8-й класс

Разделы: Математика

Класс: 8

Ход урока

I. Организационный момент.

II. Актуализация знаний.

Ключевое слово кроссворда – является темой нашего урока.

III. Новый материал.

Трапеция – (от греч. trapezion, букв. – столик).

Трапеция – четырёхугольник, у которого две стороны параллельны, а две другие – непараллельные. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.

Равнобедренная – трапеция, у которой равны боковые стороны.

Прямоугольная – трапеция, один из углов которой прямой.

Средняя линия трапеции.
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

Группы с четными номерами – исследуют диагонали равнобедренной трапеции. Группы с нечетными номерами – исследуют углы равнобедренной трапеции.

Выслушать и обсудить результаты исследования, на доске и в тетрадях записать решения.

Свойства равнобедренной трапеции.

Теорема. В равнобедренной трапеции углы при каждом основании равны.

Проведем СЕ АВ.

ABCD – параллелограмм (АВ СЕ, ВС AD).

CD = AB = CE, СDE – равнобедренный, СDЕ = СЕD.

АВ СЕ, тогда СЕD = ВАЕ, СDЕ = СЕD = ВАЕ.

ABC = 180° – СDЕ = 180° – ВАЕ = BCD.

Теорема. В равнобедренной трапеции диагонали равны.

ABC = DСВ (АВ = С, ВС – общая сторона, АВС = ВСD) тогда АС = ВD.

Сформулируйте утверждения, обратные свойствам, и выясните их справедливость.

Признаки равнобедренной трапеции.

Выслушать и обсудить результаты исследования, на доске и в тетрадях записать решения.

1. Если углы при основании трапеции равны, то она равнобедренная.

Проведем ЕС АВ.

ABCЕ – параллелограмм, тогда АВ СЕ, А = СЕD, СЕD – равнобедренный (D = СЕD), тогда СЕ = СD.

АВ = СЕ = СD, тогда АВСD – равнобедренная трапеция.

2. Если диагонали трапеции равны, то она равнобедренная.

Проведем СК ВD.

ВСКD – параллелограмм (т.к. СК ВD, ВС АК).

АСК – равнобедренный, т.к. АС = ВD = СК, САD = СDА.

СК ВD, ВDА = СКD, тогда САD = СКD.

АВD = DСА, т.к. АС=ВD, АD – общая сторона, САD = СКD, тогда АВ = СD, т.е. АВСD – равнобедренная трапеция.

Источник

Подборка задач по теме «Равнобедренная трапеция»

Подборка задач по теме «Равнобедренная трапеция»

Составила: Кобзарева И.А.

Этап введения (задачи ориентированы на знакомство с некоторыми свойствами фигуры)

1.Докажите, что трапеция в равнобедренная, если углы при основании равны

Доказать: АВС D – равнобедренная трапеция.

А D Доказательство:

2. ВС // АК (по условию).

3. АВСК – параллелограмм (по признаку параллелограмма).

4. АВ = СК (свойство параллелограмма).

5. угол ВАК = углу СК D (как соответственные при пересечении параллельных прямых АВ и СК секущей А D ).

6. угол СК D = углу С D К.

8. Из 4 и 7 следует, что АВ = D С. Ч. т. д.

Вывод: если в трапеции углы при основании равны, то трапеция равнобедренная.

2. Докажите, что трапеция равнобедренная, если диагонали равны

В С Дано: АВС D – трапеция, диагонали В D и АС равны.

Доказать: АВС D – равнобедренная трапеция.

А D Доказательство:

Рассмотрим треугольники D СВ и АВС.

Вывод: если в трапеции диагонали равны, то трапеция равнобедренная.

Этап усвоения (задачи направлены на отработку знаний свойств равнобедренной трапеции)

Задача1.(по чертежу).Найти все углы трапеции.

1) (свойство равнобедренного треугольника)

2) Пусть

3) (свойство равнобедренной трапеции)

4)

5)

(свойство равнобедренной трапеции)

6)

Ответ:

1) ABCD – равнобедренная трапеция (признак трапеции 1)

3) (гипотенуза и острый угол) => АК=Р D

4) А D = АК + КР + Р D

5) По свойству прямоугольного треугольника АВ = 2

Этап закрепления(задачи ориентированы на проверку знаний равнобедренной трапеции с использованием раннее полученных знаний)

Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как 3 к 7. Таким образом:

По условию задачи, BO + OD = 40, соответственно

Задача2. Разность оснований трапеции равна 4 см, а средняя линия 10 см. Найдите основания трапеции.

Решение.
Обозначим большее основание как а, а меньшее как b. Учтем при этом следующее:

Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме

Откуда a = b + 4, тогда

(b + 4 + b) / 2 = 10
2b + 4 = 20
b = 8
Следовательно a = b + 4 = 12
Ответ: Основания трапеции равны 8 и 12 см

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Общая информация

Похожие материалы

Контрольная работа по теме»Треугольники»

Кроссворд по геометрии на тему «Четырёхугольники» (8класс)

Конспект урока геометрии в 7 классе по теме: «Решение задач по теме: «Сумма углов треугольника»»

Презентация к уроку «Теорема Пифагора»

Таблицы по стереометрии «Призма»

Мультимедийные и гипермедийные технологии в реализации концепции эффективного изучения геометрии в начальной школе

Формирование у младших школьников представлений об окружности и круге

Презентация к уроку «Свойства пирамиды»

Не нашли то что искали?

Воспользуйтесь поиском по нашей базе из
5359620 материалов.

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

В Ленобласти педагоги призеров и победителей олимпиады получат денежные поощрения

Время чтения: 1 минута

Минпросвещения разработает внеучебные курсы для школьников

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Создана Ассоциация руководителей школ России и Беларуси

Время чтения: 1 минута

Учителя Кубани смогут получить миллион рублей на взнос по ипотеке

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник