Докажите что учение птолемея не было бесполезным
Докажите что учение птолемея не было бесполезным попс
Ответы 2
В основе системы мира Птолемея лежат четыре главных допущения: 1) Земля находится в центре Вселенной; 2) Земля неподвижна; 3) все небесные тела движутся вокруг Земли; 4) движения небесных тел происходят по окружностям с постоянной скоростью, т.е. равномерно.
Система Птолемея не только объясняла видимые движения планет, но и позволяла вычислять их положения на будущее время с точностью, удовлетворявшей несовершенным наблюдениям невооруженным глазом. Поэтому, хотя и неверная в своей основе, она сначала не вызывала серьезных возражений, а впоследствии открытые возражения против нее жестоко подавлялись христианской церковью.
Трудам Птолемея принадлежит ведущее место в становлении науки астрономии. Значение Клавдия для нее было сразу оценено по достоинству современниками. С невероятным трудом «Альмагест» связано огромное количество научной литературы.
На основании работ Птолемея современники мечтали усовершенствовать или же изменить свои труды в области науки о небесных светилах. Но все вышесказанное привело к тому, что Коперник создал свое учение, и в его основу положил труд Клавдия Птолемея.
С течением времени значение работ Птолемея не преуменьшается, а даже увеличивается. Талантливый Клавдий Птолемей в основу своих научных открытий вложил результаты своих предшественников.
Система мира Птолемея
Объяснение видимых движений планет и других небесных тел осложняется тем, что все эти движения наблюдаются нами с Земли, а ничто в наблюдениях небесных или земных явлений не указывает прямо и определенно на то, движется ли сама Земля или она неподвижна. Поэтому у древних астрономов были две точки зрения на этот вопрос:
Но допущение движения Земли слишком противоречило обычным впечатлениям и религиозным взглядам. Поэтому вторая точка зрения не могла получить подробного математического развития, и на долгое время в астрономии утвердилось мнение о неподвижности Земли.
Кто такой Птолемей?
Клавдий Птолемей – знаменитый александрийский астроном, математик и географ II века нашей эры, один из крупнейших ученых древности. В течении целого тысячелетия в области астрономии с Птолемеем никто не мог сравниться. Не сохранилось каких-либо упоминаний о его жизни и деятельности у историков этого периода. Также остались неизвестны даже примерные даты рождения и смерти Птолемея, также как и какие-либо факты его биографии.
Но благодаря своим трудам он остался в истории. К большой удаче современных историков, практически все его основные сочинения сохранились.
Собрание астрономических знаний древней Греции и Вавилона Птолемей изложил в своем труде «Великое построение», больше известном под названием «Альмагест» (до европейцев его труд донесли арабы, так звучит в переводе с греческого «мэгистос» — величайший) – труд из 13 книг.
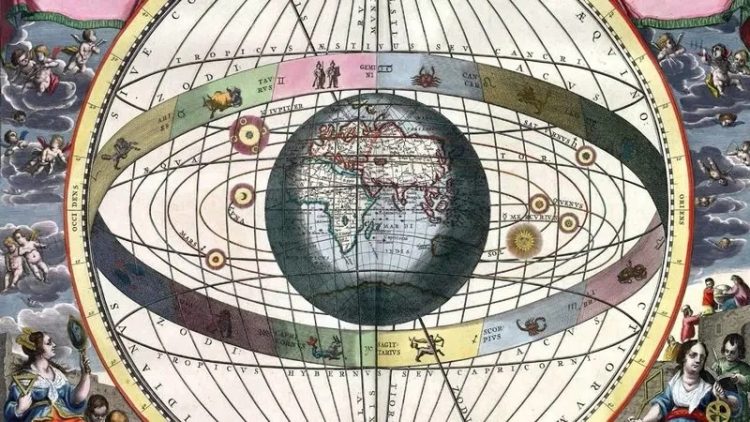
В «Альмагест» изложена геоцентрическая система мира, согласно которой Земля находится в центре мироздания, а все небесные тела обращаются вокруг нее.
Геоцентрическая система мира Птолемея
В основе своей модели Птолемей использовал математические расчеты, сделанные Евдоксом Книдским, Гиппархом, Аполлонием Пергским и самим Птолемеем. Свои положения Птолемей подтверждал опытами. Других мнений и взглядов он не признавал.
Ключевые положения, на которых строится система Птолемея
Птолемей в своей работе отразил основные принципы движения светил, а также методы и расчеты, которыми пользовался для анализа процессов, происходящих в космосе (в границах, известных на то время).
Принцип движения светил
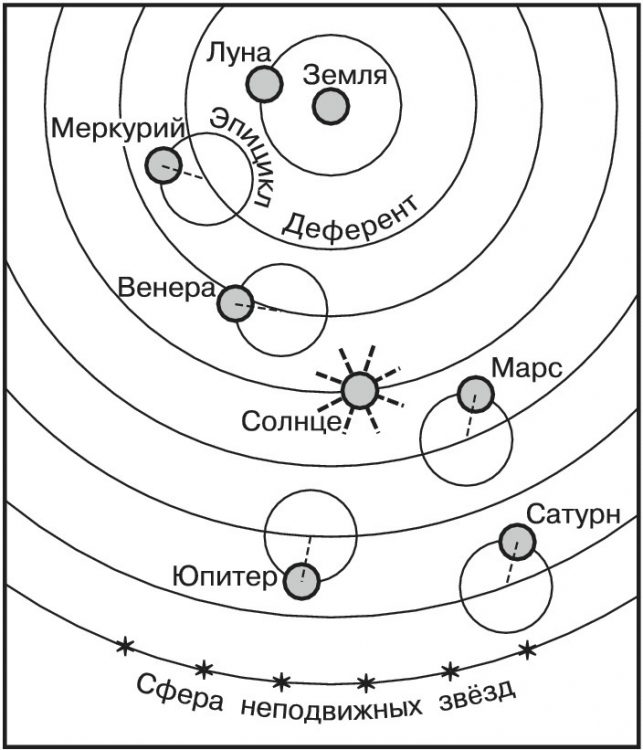
Каждая планета, согласно Птолемею, равномерно движется по кругу (эпициклу), центр которого движется по другому кругу (деференту). Это позволяет объяснить видимую неравномерность движения планет и в некоторой степени изменение их яркости.
Геоцентрическая система мира
Сама планета в системе Птолемея равномерно движется по эпициклу. С целью описать вновь открываемые неравномерности в движениях планет и Луны были введены новые дополнительные эпициклы — вторые, третьи и т.д. Планета располагалась на последнем. Теория Птолемея позволяла предвычислять сложные петлеобразные движения планет (их ускорения и замедления, стояния и попятные движения). На основе сформированных Птолемеем астрономических таблиц расположение планет можно было рассчитать с весьма высокой по тем временам точностью ( имелась погрешность менее 10′).
Кроме того, в рамках геоцентризма было необъяснимо, почему базовый период обращения по первому эпициклу для верхних планет был в точности равен году и почему Меркурий и Венера никогда не отходят далеко от Солнца, вращаясь вокруг Земли синхронно с ним.
Движение планеты по деференту у Птолемея представлялось равномерным не по отношению к центру деферента, а по отношению к особой точке, симметричной с центром Земли относительно центра деферента.
Таким образом, из основных свойств планетных движений, концепция которых была определена Птолемеем, можно выделить несколько очень важных закономерностей:
Звездный каталог
Птолемей дополнил звездный каталог Гиппарха; число звёзд в нем увеличено до 1022. Положения звёзд из каталога Гиппарха Птолемей, по-видимому, скорректировал, приняв для прецессии (прецессия — явление, при котором момент импульса тела меняет своё направление в пространстве под действием момента внешней силы) неточное значение 1˚ в столетие (правильное значение
Астрономические инструменты Птолемея
Здесь же описаны астрономические инструменты, которыми пользовался Птолемей:
Закат геоцентрического мировозрения
Система Птолемея не только объясняла видимые движения планет, но и позволяла вычислять их положения на будущее время с точностью, удовлетворявшей несовершенным наблюдениям невооруженным глазом. Поэтому, хотя и неверная в своей основе, она сначала не вызывала серьезных возражений, а впоследствии открытые возражения против нее жестоко подавлялись христианской церковью.
К началу XVI в. система Птолемея была настолько сложна, что не могла уже удовлетворить тем требованиям, которые предъявлялись к астрономии практической жизнью, в первую очередь мореплаванием.
По данным опроса, проведённого в 2011 году Всероссийским центром изучения общественного мнения (ВЦИОМ), 32 % россиян полагают, что Солнце вращается вокруг Земли!
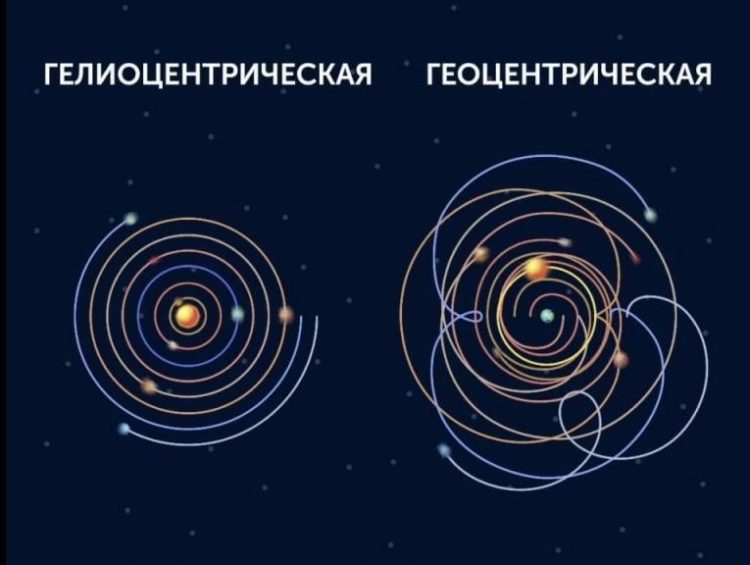
В ходе научной революции XVII века геоцентризм постепенно был оставлен учёными; постепенно утвердилась гелиоцентрическая система мира.
Геоцентрическая и гелиоцентрическая системы мира
Основными событиями, приведшими к отказу от геоцентрической системы, были создание гелиоцентрической теории планетных движений Коперником, телескопические открытия Галилея и других астрономов, открытие законов Кеплера и, главное, создание классической механики и открытие закона всемирного тяготения Ньютоном.
Интересно! По данным опроса, проведённого в 2011 году Всероссийским центром изучения общественного мнения (ВЦИОМ), 32 % россиян полагают, что Солнце вращается вокруг Земли!
Видео
Докажите что учение птолемея не было бесполезным попс
Ответы
В основе системы мира Птолемея лежат четыре главных допущения: 1) Земля находится в центре Вселенной; 2) Земля неподвижна; 3) все небесные тела движутся вокруг Земли; 4) движения небесных тел происходят по окружностям с постоянной скоростью, т.е. равномерно.
Система Птолемея не только объясняла видимые движения планет, но и позволяла вычислять их положения на будущее время с точностью, удовлетворявшей несовершенным наблюдениям невооруженным глазом. Поэтому, хотя и неверная в своей основе, она сначала не вызывала серьезных возражений, а впоследствии открытые возражения против нее жестоко подавлялись христианской церковью.
Трудам Птолемея принадлежит ведущее место в становлении науки астрономии. Значение Клавдия для нее было сразу оценено по достоинству современниками. С невероятным трудом «Альмагест» связано огромное количество научной литературы.
На основании работ Птолемея современники мечтали усовершенствовать или же изменить свои труды в области науки о небесных светилах. Но все вышесказанное привело к тому, что Коперник создал свое учение, и в его основу положил труд Клавдия Птолемея.
С течением времени значение работ Птолемея не преуменьшается, а даже увеличивается. Талантливый Клавдий Птолемей в основу своих научных открытий вложил результаты своих предшественников.
развитие психических процессов (восприятие, представления, память, мышление) на уроках культуры
Учения Птолемея
Клавдий Птолемей — крупнейших фигура в истории науки эпохи позднего эллинизма. Мировоззрение Птолемея: «Альмагест», теории движения Солнца, Луны, планет; работы по географии, оптике, математике, «Гармоники». Роль Птолемея в становлении естествознания.
| Рубрика | Астрономия и космонавтика |
| Вид | реферат |
| Язык | русский |
| Дата добавления | 03.11.2009 |
| Размер файла | 59,6 K |
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
История довольно странным образом обошлась с личностью и трудами Птолемея. О его жизни и деятельности нет никаких упоминаний у историков той эпохи, когда он жил, даже приблизительные даты рождения и смерти Птолемея неизвестны, как неизвестны и какие-либо факты его биографии.
Геоцентрическая система Птолемея противопоставляется гелиоцентрической системе Коперника, который совершил поистине революционный переворот, поставив в центр нашей планетной системы Солнце и низведя Землю до положения рядовой планеты, и якобы устранил эпициклы, показав, что они были нужны лишь для представления движения Земли вокруг Солнца.
Эта упрощенная схема, глубоко укоренившаяся среди многих лекторов, учителей, студентов и даже научных работников, на самом деле в лучшем случае неточна, а кое в чем ошибочна.
Земля у Птолемея не совпадала с центрами деферентов, а положение эпициклов и самих планет на них зависело от положения Солнца; в теории планетных движений Птолемея фигурировали и другие круги, о которых в учебниках и популярных книгах обычно не пишут (эквант, эксцентр).
В «Альмагесте» Птолемей широко использует результаты наблюдений и построения своего великого предшественника Гиппарха (II в. до н. э.). Не случайно «Альмагест» был переведен за полтора тысячелетия на столько языков и служил учебником астрономии во многих странах мира. Каждый уважающий себя ученый Арабского Востока и Средней Азии считал своим долгом составлять комментарии к «Альмагесту». Некоторые из них подвергали те или иные положения Птолемея критике.
Коперник и Кеплер в своих работах также исходили из построений Птолемея. Первый из них превратил геоцентрическую систему Птолемея в гелиоцентрическую, но сохранил принцип равномерного движения по кругам и широко использовал математический аппарат Птолемея. Второй, отказавшись от этого принципа, тем не менее использовал построения Птолемея, чтобы найти истинную форму планетных орбит. Обо всем этом мы расскажем ниже.
Кроме «Альмагеста» Птолемей оставил ряд других сочинений, причем не только по астрономии, но и по математике, оптике, географии, музыке. Ему принадлежит разработка основ математической картографии и составление списка координат 8000 географических пунктов (определенных, правда, весьма приближенно).
По-видимому, своими успехами в области астрономии Птолемей во многом обязан знаменитой Александрийской библиотеке, которой он широко пользовался. Так стали ему известны труды Гиппарха (не дошедшие, увы, до нас), а также таких древнегреческих ученых, как Метон (V в. до н. э.), Евклид, Аристотель, Каллини (IV в. до и. э.), Аристилл, Тимохарис, Архимед, Аристарх Самосский, Эратосфен (III в. до н. э.), Аполлоний Пергский (III—II вв. до и. э.). Птолемей широко использовал также наблюдения астрономов Вавилона, не называя их, правда, по именам. Это в основном наблюдения лунных и солнечных затмений, а также некоторых других явлений (покрытий звезд Луною, соединений планет), проводившиеся вавилонскими астрономами начиная с VIII в. до н. э. Эти наблюдения послужили Птолемею для создания теории движения Луны, которой пользовались десятки поколений астрономов, моряков, путешественников.
Деление философии на теоретическую и практическую заимствовано Птолемеем у Аристотеля. Надо сказать, что в ту эпоху (и много позднее тоже) философией называли науку о природе вообще. Теоретическая философия делилась на три раздела: теологию, математику и физику. Это деление принимает и Птолемей.
«Первопричину первого движения вселенной, попросту говоря, можно рассматривать как некое невидимое и неподвижное божество; раздел теоретической философии, изучающий это, может быть назван теологией, поскольку этот вид деятельности можно представить себе только где-то высоко, вплоть до высочайших пределов вселенной, и он полностью отделен от ощутимой реальности»,— пишет Птолемей.
Математика, по Птолемею, изучает числа, а также форму, размеры, место, время и другие свойства, выражаемые числами. И не случайно свое сочинение он назвал математическим построением.
В своем мировоззрении Птолемей почти точно следует Аристотелю. И дело, разумеется, не столько в геоцентризме обоих, сколько в их взгляде на основные категории бытия. Вслед за Аристотелем Птолемей считает все сущее состоящим из материи, формы и движения, причем ни одна из этих категорий не может существовать без двух других. Это значит, что материя не может существовать без движения и движение нельзя себе представить без материи.
В своем конспекте «Метафизики» Аристотеля В.И. Ленин отмечал его материалистический подход как к вопросу о реальном существовании вещей, так и к классификации наук. «Прелестно! Нет сомнений в реальности внешнего мира»,— записывает В.И. Ленин. Очевидно, что этот отзыв может быть распространен и на взгляды Птолемея.
Уже из приведенных выше выдержек из «Альмагеста» ясно, что Птолемей допускал (вместе с Аристотелем) «первый толчок», допускал существование божества. Но это божество играет во взглядах Птолемея весьма ограниченную роль: оно только создало и пустило в ход «небесный механизм», управляющий движениями светил небесных. Больше о боге и о его влиянии на процессы во Вселенной в «Альмагесте» не говорится ничего.
Не лучше, чем к физике, выглядит отношение Птолемея и к теологии. Теология в его описании предстает перед нами как нечто столь же возвышенное, сколь и неясное. Правда, у Птолемея есть целый труд, посвященный астрологии,— «Четырехкнижие», но не следует отождествлять приверженность к астрологии с отношением к религии. В «Четырехкнижии» Птолемей пытается обосновать некие физические воздействия небесных светил на земные явления, иначе говоря, он пытается подвести некоторый физический «базис» под астрологические представления. Этот вопрос мы рассмотрим отдельно (в гл. 15), здесь же для нас важно то, что астрология Птолемея не была основана на религиозных представлениях.
Таким образом, по своим религиозным убеждениям Птолемей был весьма умеренным деистом, иначе говоря, он признавал существование бога, но не приписывал ему никаких конкретных функций, за исключением создания мира и «первого толчка».
С этой точки зрения историческим курьезом является то обстоятельство, что спустя тысячу лет учения Аристотеля и Птолемея были официально признаны христианской церковью как истинные. Правда, произошло это далеко не сразу. Первые переводы трудов Аристотеля и Птолемея на латинский язык появились в Европе в конце XII в; это были переводы с арабского. Переводы работ Аристотеля непосредственно с греческого были сделаны (Вильгельмом Мербекским) уже в 60-х годах XIII в. Вскоре после этого взгляды Аристотеля подверглись жестоким нападкам со стороны доминиканцев, в первую очередь Альберта Великого (1206—1280) и Фомы Аквинского (1225—1274). Вместе с тем оба они приложили немало усилий, чтобы с помощью хитроумно составленных комментариев приспособить, адаптировать учение Аристотеля к канонам христианской религии. Альберт Великий положительно относился и к системе мира Птолемея. В начале XIV в. она приобрела известное влияние в христианском мире, а в середине XIV в. получила полное признание сначала во Франции, а потом и в других странах.
Причин такого отношения христианской церкви к сочинениям «язычников» Аристотеля и Птолемея было несколько. Одна из них состояла в том, что учения обоих ученых были основаны на геоцентрической системе мира, полностью удовлетворявшей догмам христианства о том, что человек создан богом по своему образу и подобию, а потому он должен жить на неподвижной Земле, в центре мира. О других причинах мы скажем ниже.
Рассмотрим геоцентризм Птолемея, опираясь на его собственное изложение в I книге «Альмагеста». Доказав, что небесный свод подобен сфере (что позволяет использовать для определения видимых положений светил сферические координаты), а также, что и Земля имеет форму шара (что тоже позволяет применять сферические координаты точек земной поверхности: долготу и широту), Птолемей переходит к доказательству того, что Земля находится в середине небесного свода, в центре небесной сферы.
Доказательства центрального положения Земли, которые мы только что привели, основаны на двух ошибочных предположениях. Во-первых, это предположение о том, что размеры небесной сферы, хотя и очень велики, но конечны, а потому смещение Земли внутри небесной сферы к одному из полюсов приведет к неравенству северного и южного сегментов (здесь уже нельзя сказать «полусфер»). Во-вторых, это предположение, что суточное вращение небесной сферы происходит само по себе, независимо от Земли. Но мы знаем, что это вращение является лишь отражением реального вращения Земли вокруг оси, а потому второе предположение Птолемея ошибочно в своей основе. Что касается первого предположения, то несомненно, что Птолемей обсуждал все возможные последствия сдвига Земли из центра сферы, пользуясь моделью, где маленький шарик (Земля) находился внутри большого полого шара (небесной сферы). Мы знаем, что расстояния до звезд настолько велики, что даже движение Земли вокруг Солнца по орбите диаметром 300 миллионов километров не приводит к заметным смещениям звезд. Эти смещения (годичные параллаксы звезд) оказались столь малы, что понадобилось 17 столетий после Птолемея и два с лишним столетия после изобретения телескопа, чтобы они смогли быть обнаружены.
После доказательства центрального положения Земли Птолемей доказывает ее неподвижность в пространстве. В самом деле, утверждает он, если бы Земля имела какое-либо движение, она бы смещалась со своего центрального положения, и тогда имели бы место те же эффекты, как и в случае нецентрального положения Земли относительно небесной сферы. Но так как эти эффекты не наблюдаются, значит, Земля неподвижна.
Вторым доказательством неподвижности Земли, которое приводит Птолемей, является вертикальное свободное падение тел во всех местах Земли. Все тела стремятся к центру, и поскольку они падают вертикально вниз на всех широтах Земли, значит, она и есть этот центр., И если бы земная поверхность не преграждала путь падающим телам, они падали бы дальше вниз, до самого центра Земли. И хотя Земля велика и тяжела, не следует удивляться тому, что она никуда не падает и не требует опоры. Ведь Земля мала по сравнению с Вселенной, которая оказывает на нее равномерное давление со всех сторон, а потому Земля и не может никуда сдвинуться. Земля тяжелее известных нам падающих тел, а потому, если бы она тоже могла куда-нибудь падать, она падала бы быстрее, и мы не могли бы этого не заметить.
Дальше Птолемей вступает в полемику со сторонниками вращательного движения Земли, не называя их, правда, по именам. Очевидно, он имеет в виду Гераклита Понтийского и Аристарха Самосского, считавших, что суточное вращение совершает Земля, а не небо. Птолемей признает, что среди небесных явлений нет ничего, противоречащего гипотезе о вращении Земли, но совсем иначе обстоит дело с явлениями на земле и в воздухе. «Они должны допустить,— пишет Птолемей,— что вращательное движение Земли должно быть самым быстрым из всех движений, связанных с ней, учитывая, что Земля должна совершать одно обращение за столь короткое время; в результате все предметы, не опирающиеся на Землю, должны казаться совершающими такое же движение в обратном направлении; ни облака, ни другие летающие или парящие объекты никогда не будут видимы движущимися на восток, поскольку движение Земли к востоку будет всегда отбрасывать их, так что эти объекты будут казаться движущимися на запад, в обратном направлении». Даже если предположить, рассуждает далее Птолемей, что и воздух движется в том же направлении и с той же скоростью, что и Земля, плавающие и парящие в воздухе тела не должны следовать его движению. Если же они связаны с воздухом так, что следуют его движению, то нам они казались бы неподвижными, чего на самом деле нет.
Птолемей не обсуждает предположения Аристарха о движении Земли вокруг Солнца. По-видимому, покончив с гипотезой о вращении Земли вокруг оси, он не счел нужным даже упоминать о более сложном и крупномасштабном движении Земли. Тем более что приведенные им аргументы говорили вообще против любого движения Земли.
Но в приведенных выше рассуждениях Птолемея, кроме тех наивных аргументов, о которых мы говорили, есть и здравые мысли. Так, подчеркнем мысль Птолемея, что ход небесных явлений не противоречит гипотезе о вращении Земли. Птолемеи прав и в том, что вращательное движение Земли быстрее всех прочих известных в ту эпоху движений. Если бы он попробовал вычислить ее скорость (а у него были для этого все необходимые данные: окружность Земли по Эратосфену и широта Александрии), он нашел бы эту величину равной 385 м/с, что в десять раз быстрее ураганного ветра. Но он не мог понять, что воздух увлекается вращением Земли, а все плавающие или летающие в воздухе тела тоже участвуют во вращении Земли.
Таким образом, Птолемей предстает перед нами как последовательный геоцентрист. Но свой геоцентризм он старается обосновать соображениями, основанными на физике явлений, а не схоластическими рассуждениями или ссылками на авторитеты.
Остановимся несколько подробнее на значении второй из перечисленных причин. Математическое описание движений планет, Солнца и Луны в системе мира Птолемея достигло такой точности, что позволяло предвычислять положения этих светил на небе, а также наступление некоторых небесных явлений, связанных с их движением (например, солнечных и лунных затмений), с весьма высокой для того времени точностью. Таким образом, математическая модель Птолемея имела большую прогностическую ценность.
В то же время христианская церковь в странах Европы в результате ряда объективных факторов взяла на себя роль «хранителя учености». От периода заката античной науки (совпавшего с развитием христианства) и до начала эпохи Возрождения христианские богословы были практически единственными носителями знания. Конечно, отдавая первенствующее место среди наук того времени богословию и подчеркивая его превосходство над философией, эти деятели исходили из ошибочных философских позиций. С этих же позиций они начиная с XIII в. адаптировали, приспособили для своих целей идеи Аристотеля и математические построения Птолемея.
Эти причины способствовали сохранению господства системы Птолемея в науке на протяжении полутора тысяч лет.
Небесная сфера: расчеты и измерения
Затем Птолемей вводит понятие о хорде угла. Птолемей доказывает несколько теорем, которые позволяют ему составить таблицу хорд всех углов от 0 до 180°.
Имея хорды нескольких углов, Птолемей доказывает теорему, что хорда разности двух углов может быть найдена, если известны хорды этих двух углов. Для этого он прежде доказывает другую теорему, которую можно сформулировать так: произведение диагоналей произвольного четырехугольника, вписанного в окружность, равно сумме произведений его противоположных сторон. Эта теорема получила название теоремы Птолемея.
Есть указания, что таблица хорд, рассчитанная по формуле хорд половинных углов (без формул хорд сумм и разностей углов), была составлена еще Гиппархом. Но в столь полном виде, да еще с первыми разностями (приращениями хорды на один градус угла), она, несомненно, была вычислена Птолемеем впервые.
Из этого примера мы видим, каким усердным математиком и вычислителем был Птолемей. Стоит сравнить его в этом отношении с Иоганном Кеплером, которому в поисках истинной формы планетных орбит также приходилось по многу раз производить одни и те же вычисления, чтобы согласовать наблюдения Марса с теорией. Рассказывая в «Новой астрономии» о ходе своей работы по вычислениям (методом проб и ошибок) радиуса орбиты Марса, долготы его афелия и расстояний от центра круговой (тогда еще круговой!) орбиты Марса до Солнца и до центра экванта, Кеплер писал: «Если этот обременительный способ работы вам не нравится, вы можете справедливо пожалеть меня, поскольку я вынужден был проделать это по меньшей мере 70 раз с большой затратой времени». Сохранившиеся до нашего времени черновики расчетов Кеплера занимают 900 листов, исписанных мелким почерком.
Покончив с определением и табулированием хорд (напоминаем, что хорды заменяют ему весь набор современных тригонометрических функций), Птолемей развивает основные положения и теоремы сферической тригонометрии. Важное место среди них занимают две теоремы Менелая о соотношениях хорд дуг четырех больших кругов, пересекающих друг друга. Птолемей доказывает, что эти дуги связаны соотношениями которые в переводе на современные обозначения имеют вид
Эти теоремы были впервые доказаны александрийским математиком и астрономом Менелаем, жившим и работавшим во второй половине I в. н. э. Птолемей и здесь не делает ссылки на приоритет Менелая (как не ссылается он на Евклида и Архимеда), хотя он не мог не читать его «Сферику», где изложены эти теоремы. В дальнейшем он упоминает лишь о наблюдениях Менелая.
Далее Птолемей вводит понятия sphaera recta (прямая сфера) и sphaera obliqua (наклонная сфера), которыми он в дальнейшем неоднократно пользуется. Под «прямой сферой» он понимает такое положение небесной сферы, когда небесный экватор перпендикулярен горизонту (мы знаем, что такое расположение обоих больших кругов наблюдается на экваторе). Под «наклонной сферой» Птолемей понимает любое другое положение небесной сферы, когда экватор наклонен к горизонту под острым углом.
Для нас эти термины звучат немного странно, но ведь именно от «прямой сферы» берет начало всем известный термин прямое восхождение (одна из двух сферических координат в экваториальной системе). В самом деле, если наблюдатель расположен па экваторе, разность времен восхода светила и точки весеннего равноденствия, переведенная в единицы дуги (помня, что 1 ч соответствует дуге в 15°), как раз и будет прямым восхождением светила. Если точка весеннего равноденствия находится на горизонте, то дуга, которую прошло светило с момента его восхода, также будет равна прямому восхождению.
Следующей задачей, которую решает Птолемей, является вычисление «таблицы наклонений», как она названа кем-то из переписчиков или переводчиков «Альмагеста», а точнее, склонений точек на эклиптике в функции дуг самой эклиптики (т. е. небесных долгот), отсчитываемых от точки весеннего равноденствия через градус. Именно для этого расчета Птолемею и была нужна первая теорема Менелая.
В наше время расчет склонений центра диска Солнца (который движется по эклиптике) или интересующих нас точек на эклиптике делается без громоздкой теоремы Менелая, с помощью формул сферического треугольника, образованного дугами эклиптики, экватора и круга склонения данной точки. Птолемей не мог решать сферический треугольник современным способом не только из-за отсутствия в то время понятия косинуса, столь же нужного в формулах сферической тригонометрии, как и синус (последний можно было заменить хордой двойного угла), но и потому, что в эти формулы входят функции двугранных углов (например, между плоскостями экватора и эклиптики), а Птолемей мог иметь дело только с дугами. И хотя он использует угол наклона эклиптики к экватору, но, в сущности говоря, он оперирует не с двугранным углом, а с дугой колюра солнцестояний, равной наибольшему расстоянию эклиптики от экватора.
Своей дотошностью подходит Птолемей к изложению своих математических методов. Его доказательства теорем безукоризненны с точки зрения математической логики и в то же время просты и понятны. Свои построения он поясняет чертежами. Так и кажется, что он писал свою книгу в расчете не на таких же маститых астрономов, как он сам, а на студентов. И действительно, «Альмагест» в течение полутора тысяч лет был стандартным учебником астрономии: по нему учились будущие ученые и студенты в первых европейских университетах.
Во второй книге своего труда Птолемей ставит и решает ряд задач, как бы мы выразились теперь, практической астрономии. Прежде всего он уточняет, что «наша часть обитаемого мира» находится в северном полушарии и занимает по долготе менее 180°. Неясно, какими данными располагал Птолемей для последнего вывода. Долготы были известны далеко не для всех стран, о которых мог знать Птолемей. Так, он знал о существовании Британии далеко на западе и, несомненно, Индии и Китая на востоке (о них должны были рассказывать ему александрийские и иностранные купцы). Но достоверное определение разности долгот он имел лишь одно: лунное затмение—330 сентября 20 наблюдалось одновременно в Карфагене (долгота ок. 10°) и в Арбеле, на реке Тигр (долгота ок. 46°). Об этом факте сообщается в «Географии» Птолемея, Тем не менее он был прав в своих представлениях о расположении «нашей части обитаемого мира».
После этого введения Птолемей ставит и решает следующие практические задачи:
1) определить угловое расстояние полюса от горизонта или (равное ему) зенитное расстояние небесного экватора, измеряемое вдоль небесного меридиана;
2) для тех мест, где Солнце достигает зенита, определить, когда и как часто это происходит;
3) определить отношения полуденных теней от гномона в дни равноденствий и солнцестояний;
4) определить разность между длительностью самого длинного и самого короткого дня и длиной дня во время равноденствий;
5) определить приращение и убывание длительности дней и ночей в разные времена года;
6) определить дуги экватора, которые восходят и заходят одновременно с заданными дугами эклиптики (эта задача нужна для вычисления так называемых гелиакических восходов и заходов);
7) определить величины углов между эклиптикой и наиболее важными большими кругами: небесным меридианом, горизонтом и кругом высоты (большим кругом, проходящим через зенит и надир).
Результаты своих расчетов Птолемей приводит в виде таблиц.
Однако Птолемей не только доказывал теоремы и производил вычисления, он еще и вел наблюдения. Это были в основном позиционные наблюдения, сводившиеся к определению астрономических координат небесных светил.
Трудность определения астрономических координат из наблюдений состоит в том, что ни точка весеннего равноденствия (начало отсчета прямого восхождения и долготы), ни экватор, ни эклиптика ничем на небе не обозначены. Как выходил из этого затруднения Птолемей (а до него Гиппарх), мы скоро узнаем.
Птолемей дает уже в конце первой книги описание одного из своих приборов. Правда, он не изобразил ни одного из них хотя бы схематически, но по его подробным описаниям это сделали исследователи его трудов.
Схемы приборов Птолемея, воспроизводимые в этой книге, заимствованы у них.
В пятой книге (гл. 12) Птолемей описывает третий угломерный прибор, названный им параллактическим инструментом. Такое название Птолемей дал этому прибору потому, что он использовал его для определения параллакса Луны.
Параллактический прибор Птолемея, получивший впоследствии название трикветр, применялся многими астрономами после него. Его описание и чертеж мы находим в классическом труде Коперника «О вращениях. », а также в «Механике обновленной астрономии» Тихо Браге. Именно он изображен на знаменитой картине польского художника Яна Матейки «Коперник» (1873 г.). Интересно, что подлинный трикветр Коперника спустя 40 лет после его смерти попал в руки Тихо Браге и был им подробно описан в вышеупомянутой книге, вышедшей в 1598 г.
Однако наблюдения с этим прибором требовали известного навыка со стороны наблюдателя. В отличие от современных астрономических приборов, в которых наведение на светило осуществляется поворотом трубы прибора вокруг двух взаимно перпендикулярных осей, в астролябии Птолемея нужно было поворачивать подвижные части прибора вокруг трех осей: вокруг полярной оси dd, вокруг оси эклиптики ее и вокруг оси колец 1 и 2, лежащей в плоскости эклиптики (по аналогии с осью склонений современных телескопов-экваториалов ее можно назвать осью широт).
Впоследствии, в 1581 г., искусный наблюдатель Тихо Браге воспроизвел по описанию Птолемея его прибор, назвав его «зодиакальными армиллами» (слово «армилла» означает «кольцо»; Тихо Браге употреблял это слово во множественном числе). Видимо, этот прибор не удовлетворил Тихо Браге, и спустя три года он заменил его «экваториальными армиллами», где, кроме меридиана, имеются лишь два кольца: небесный экватор и круг склонения, а поворот осуществляется вокруг двух взаимно перпендикулярных осей: полярной и оси склонений.
С помощью описанных здесь приборов Птолемей и производил все свои наблюдения положений небесных светил. Естественно, все они велись невооруженным глазом. Их точность зависела от точности наведения шпеньков или диоптров, от правильности установки самого инструмента, наконец, от точности делений и их правильного считывания (большинство наблюдений проводилось ночью). Точность наблюдений Птолемея не превышала 10 мин дуги. Еще ниже была точность наблюдений, связанных с регистрацией времени (моменты затмений, покрытий звезд Луной, прохождений светил через меридиан). Точных часов в те времена не было, а существовавшие солнечные, песочные и водяные часы давали точность не выше 15 мин времени, что в переводе на единицы угла могло привести к ошибкам в определении прямых восхождений и эклиптикальных долгот в 3-4°.
Теория движения Солнца
На основании принятой им длины года Птолемей вычисляет среднее суточное движение Солнца по эклиптике (по долготе) и находит, что в шестидесятеричной записи оно равно, что соответствует в привычных нам единицах.
Умножая на 365 (число дней в египетском году), он находит среднее годовое движение Солнца, или, что то же самое, приращение его долготы за один египетский год:
Только аль-Баттани (850—929), имея в распоряжении наблюдения, сделанные на десять с лишним столетий после Гиппарха, когда длительность сезонов заметно изменилась, смог вычислить смещение перигея Солнца. К тому времени оно достигло 16°.
Эти обстоятельства (недостаточная точность наблюдений Гиппарха и Птолемея) были выяснены более 40 лет назад бельгийским историком науки А. Ромом, затем на него указали голландские исследователи В. Петерсен и О. Шмидт. (Однако наш расчет был выполнен совершенно независимо и другим методом, чем у них). Авторы указанных работ показали, что ошибка в определении момента солнцестояния или равноденствия всего на 1 ч (!) привела бы к погрешности в определении положения перигея на 1°. Но точность в 1 ч была недоступна ни Гиппарху, ни Птолемею.
Птолемей приводит таблицу аномалий движения Солнца, т. е. величины х в функции угла М при его изменении от 0 до 360°. Максимальное значение этой величины у него, как мы уже говорили, равно 2°23′ (по Гиппарху).
Последний вопрос, который рассматривает Птолемей в книге III «Альмагеста», это вопрос о неравенстве длительности суток.
Уравнение времени складывается из двух составляющих: уравнения от наклона эклиптики, график которого имеет вид синусоиды с двумя максимумами и двумя минимумами (в дни равноденствий и солнцестояний оно равно нулю), и уравнения от эксцентриситета, выражаемого синусоидой с одним максимумом и одним минимумом (в дни прохождения Солнца через перигей и апогей оно равно нулю). Суммарная кривая, отражающая оба эффекта, имеет более сложный вид: с двумя неравными максимумами и двумя минимумами. На рис. 16 изображен современный график уравнения времени и обеих его составляющих. В эпоху Птолемея этот график имел несколько иной вид все из-за того же смещения солнечного перигея и апогея. Как уже говорилось, Солнце тогда проходило эти точки примерно на месяц раньше, чем в наши дни. Поэтому кривую уравнения от эксцентриситета следует сместить на один месяц влево.
Во времена Птолемея не умели чертить графиков. В геометрических построениях пользовались только циркулем и линейкой: Птолемей мог вычислить таблицу уравнения времени на каждый день года. Но он не сделал этого. Зато он дал подробные указания к вычислению этой величины, а также (с ее учетом) долготы истинного Солнца на любой день любого года.
Птолемей ввел ряд важных понятий, используемых в астрономии и поныне. К ним относятся и понятие среднего Солнца, и среднего суточного движения, и понятие средней долготы, и уравнение времени. Так что не следует с его именем связывать одни эпициклы, как это делают некоторые авторы популярных книг, преподаватели или лекторы.
Теория движения Луны
Были наблюдения солнечных и лунных затмений, выполненные в древнем Вавилоне, затем в Греции, на Родосе (Гиппархом) и в Александрии (в том числе его собственные наблюдения), почти за девять веков. Были позиционные наблюдения Гиппарха и его, Птолемея. Были точные определения длительности четырех лунных месяцев, полученные Гиппархом из его знаменитых циклов. Были основы теории, заложенные тем же Гиппархом. Дальше надо было действовать самому.
И вот перед нами книга IV «Альмагеста». Птолемей ни на минуту не забывает, что он пишет руководство по астрономии, хотя, конечно, не имеет представления о том, что пишет на века. И не на один-два века, а на целых пятнадцать.
Дальше Птолемей начинает вычислять первое, или простое, неравенство в движении Луны, аналогичное первому неравенству в движении Солнца. Еще раз доказав эквивалентность моделей с эксцентром и с эпициклом, он для дальнейших операций выбирает модель с эпициклом (эксцентр ему еще понадобится). Первое неравенство вызвано, по Птолемею, эксцентричным положением орбиты Луны относительно Земли. Но ради удобства геометрических построений и основанных на них расчетов Птолемей строит такую модель