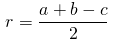Докажите что в прямоугольном треугольнике гипотенуза больше катета

Источник

Геометрия

Именная карта банка для детей
с крутым дизайном, +200 бонусов

Закажи свою собственную карту банка и получи бонусы

План урока:

Теорема Пифагора

Попытаемся установить связь между гипотенузой и катетами прямоугольного треугольника. Пусть в некотором прямоугольном треуг-ке катеты имеют длины а и b, а гипотенуза равна с. Пусть один из острых углов треуг-ка составляет α, тогда другой острый угол должен равняться 90 – α:

Далее возьмем 4 таких треуг-ка и расположим их следующим образом:

Здесь мы прикладываем треуг-ки так, чтобы их разные катеты образовали одну сторону четырехугольника. В результате получается большой квадрат со стороной a + b. Квадратом он является по определению, ведь все его стороны одинаковы, а углы – прямые.

Изучим центральную фигуру, чью площадь мы обозначили как S₂. Это четырехуг-к, причем все его стороны равны с, то есть длине гипотенузы треугольника. С другой стороны, каждый его угол можно найти, вычтя из 180° величины α и 90° – α:

Получается, что всего его углы прямые, то есть он является квадратом. Найдем его площадь:

Вернемся к большому квадрату. С одной стороны, его площадь можно записать как сумму площадей фигур, его составляющих:

Cдругой стороны, эту же площадь можно найти, просто возведя в квадрат его сторону:

Получили формулу, в которой и заключен смысл теоремы Пифагора:

Изучим несколько простейших примеров использования теоремы Пифагора.

Задание. Длины катетов прямоугольного треугольника составляют 5 и 12. Определите длину гипотенузы.

Решение. Запишем теорему Пифагора:

Задание. Длина катета треугольника составляет 3, а гипотенузы – 5. Какова длина другого катета?

Решение: На это раз нам известен один из катетов а = 3 и гипотенуза с = 5. Подставим в теорему Пифагора эти числа:

Теорема Пифагора имеет огромное значение для геометрии и смежных дисциплин. Приведенное здесь ее доказательство является одним из простейших, но отнюдь не единственным. Сегодня человечеству известно 367 различных доказательств теоремы Пифагора, что лишь показывает ее огромную значимость.

На самом деле Пифагор, известный древнегреческий математик, не был первым, кто обнаружил это равенство. Пифагор родился примерно в 570 г. до н. э., однако ещё египтяне знали про прямоугольный треуг-к со сторонами 3, 4 и 5. Поэтому его часто именуют египетским треугольником.

Также вычислять стороны прямоугольного треуг-ка умели и в Вавилоне уже за 1000 лет до рождения Пифагора. Вероятно, Пифагор узнал о формуле от вавилонян, а сам лишь вывел ее доказательство (вавилоняне не утруждали себя необходимостью доказывать теоремы геометрии). Утверждается, что Пифагор принес сделал жертвоприношение в размере 100 быков после того, как смог доказать теорему.

Задание. Вычислите гипотенузу равнобедренного прямоугольного треуг-ка, чьи катеты имеют единичную длину.

Решение. В теорему Пифагора вместо букв a и b подставим единицу:

Обратите внимание, что в данной задаче в качестве длины гипотенузы прямоугольного треугольника получилось иррациональное число. Исторически именно при решении подобной задачи люди (это были ученики Пифагора) впервые столкнулись с иррациональными числами. Перед дальнейшим изучением темы есть смысл вспомнить основные правила вычислений с квадратными корнями.

Задание. На рисунке построен произвольный квадрат. Предложите способ, как построить квадрат с вдвое большей площадью.

Решение. Проведем в исходном квадрате диагональ. Далее построим новый квадрат со стороной, равной этой гипотенузе:

Запишем для одного из них теорему Пифагора:

Но площадь квадрата равна его стороне, возведенной во вторую степень, поэтому величина с 2 – это площадь большого (на рисунке – синего)квадрата, а х 2 – площадь маленького:

Подставим эти выражения в формулу, выведенную из теоремы Пифагора, и получим, что площадь большего квадрата ровно вдвое больше:

Задание. Найдите площадь равнобедренного прямоугольного треуг-ка, гипотенуза которого имеет длину 10.

Решение. Обозначим катеты переменной х, тогда теорема Пифагора будет выглядеть как уравнение:

Задание. Один из острых углов прямоугольного треугольника составляет 30°, а его гипотенуза равна 10. Найдите оба катета.

Решение. Мы знаем, что в прямоугольном треуг-ке с острым углом 30° гипотенуза вдвое длиннее меньшего катета (он как раз лежит против угла 30°), мы можем найти этот катет:

Другой катет находим с помощью теоремы Пифагора:

Задачи на применение теоремы Пифагора

Теорема Пифагора используется в огромном количестве геометрических задач. С ее помощью можно находить диагонали некоторых четырехуг-ков, длины высот, вычислять площади.

Задание. Стороны прямоуг-ка имеют длину 8 и 15 см. Найдите длину его диагонали.

Решение. Рассмотрим произвольный прямоугольник АВСD. Если в нем провести диагональ ВD, то получится прямоугольный треуг-к АВD. Пусть АВ = 15, АD = 8. Запишем теорему Пифагора для ∆АВD:

Задание. В равнобедренном треуг-ке основание имеет длину 16 см, а боковые стороны составляют 17 см. Найдите длину высоты, проведенной к основанию этого треуг-ка, а также площадь треуг-ка.

Решение. Напомним, что высота, опущенная к основанию равнобедренного треуг-ка, одновременно является и медианой, и биссектрисой. Это значит, что Н – середина АВ. Тогда можно найти длину отрезков АН и НВ:

Теперь можно рассмотреть ∆АСН. Он прямоугольный, и нам известно его гипотенуза (она является боковой стороной ∆АВС и по условию равна 17 см) и катет АН. Тогда можно найти и второй катет, то есть высоту СН:

Задание. Высота равностороннего треуг-ка составляет 4 см. Найдите его сторону.

Решение. Напомним, что в равностороннем треуг-ке все углы равны 60°. Также учтем, что высота в равностороннем треуг-ке является также и биссектрисой и медианой:

Рассмотрим ∆АСН. Он прямоугольный, и один из его углов составляет 60°. Значит, другой угол составляет 30°. Но в таком треуг-ке гипотенуза вдвое больше катета, лежащего против ∠30°:

Обратите внимание, мы специально домножили дробь на корень из 3, чтобы корень оказался в числителе, а не знаменателе. Т.к. в таком виде проще работать с квадратными корнями.

Итак, мы нашли АН. Теперь можно найти сторону АС, которая вдвое длиннее:

Задание. Составьте формулу для нахождения площади равностороннего треуг-ка, если известна только его сторона.

Решение. Обозначим сторону треуг-ка буквой а. Для вычисления площади необходимо найти высоту:

Как и в предыдущей задаче, отрезок АС вдвое длиннее АН:

Высоту мы нашли. Осталось найти площадь:

Задание. В прямоугольном треуг-ке, катеты которого имеют длину 60 и 80, проведена высота к гипотенузе. Найдите высоту гипотенузы, а также длину отрезков, на которые эта высота разбивает гипотенузу.

Решение. Найдем длину гипотенузы ВС:

Осталось найти длины отрезков СН и НВ. Для этого необходимо записать теорему Пифагора для ∆АСН и ∆АНВ, которые являются прямоугольными. Начнем с ∆АСН:

Аналогично работаем и с ∆АНВ:

Можно проверить себя. Отрезки НВ и СН вместе составляют отрезок СВ, поэтому должно выполняться равенство:

Задание. Диагонали ромба равны 10 и 24 см. Чему равна его сторона?

Пусть в ромбе АВСD диагонали пересекаются в точке О, причем АС = 24 см, а ВD = 10 см.Напомним, что диагонали ромба пересекаются под углом 90° и делятся при этом на одинаковые отрезки. Следовательно, ∆АВО прямоугольный. Найдем его катеты:

Задание. Основания равнобедренной трапеции имеют длину 20 и 10, а боковая сторона имеет длину 13. Найдите площадь трапеции.

Решение. Опустим на большее основание две высоты:

В итоге получили прямоуг-к АВКН. Его противоположные стороны одинаковы, поэтому

∆АНD и ∆ВКС равны друг другу, ведь это прямоугольные треуг-ки с одинаковой гипотенузой (АD = ВС, ведь это равнобедренная трапеция) и равным катетом (АН = ВК как стороны прямоуг-ка). Это значит, что DH = КС. Но эти отрезки вместе с НК составляют CD. Это позволяет найти DH и KC:

Зная высоту трапеции и ее основания, легко найдем и ее площадь:

Пифагоровы тройки

Возможно, вы уже заметили, что в большинстве школьных задач на применение теоремы Пифагора используются треуг-ки с одними и теми же сторонами. Это треуг-к, чьи стороны имеют длины

Их использование обусловлено тем, что все их стороны выражаются целыми числами. В задачах же, например, с равнобедренным прямоугольным треуг-ком хотя бы одна из сторон обязательно оказывается иррациональным числом.

Прямоугольные треуг-ки, у которых все стороны являются целыми, называют пифагоровыми треугольниками, а длины их сторон именуются пифагоровыми тройками. Получается, что пифагоровыми называются такие тройки натуральных чисел а, b и с, которые при подстановке в уравнение

обращают его в справедливое равенство.

Для удобства такие тройки иногда записывают в скобках.

Например, тройка чисел (3; 4; 5)– пифагорова, так как

Задание. Определите, какие из следующих троек чисел являются пифагоровыми:

Несложно догадаться, что пифагоровых троек существует бесконечно много. Действительно, возьмем тройку (3; 4; 5). Далее умножим все числа, составляющие ее, на два, и получим новую тройку (6; 8; 10), которая также пифагорова. Умножив исходную тройку на 3, получим тройку (9; 12; 15), и она снова пифагорова. Вообще, умножая числа пифагоровой тройки на любое натуральное число, всегда будем получать новую пифагорову тройку. А так как натуральных чисел бесконечно много, то и троек Пифагора также бесконечное количество.

Отдельно выделяют понятие примитивной пифагоровой тройки. Эта такая тройка, числа которой являются взаимно простыми, то есть не имеют общих делителей. Другими словами, примитивная тройка НЕ может быть получена из другой тройки простым умножением ее чисел на натуральное число. В частности, тройка (3; 4; 5)является примитивной, а «производные» от нее тройки (6; 8; 10) и (9; 12; 15) уже не примитивные.

Интересно, что примитивных троек также бесконечно много. Ещё Евклид предложил алгоритм для их поиска, который, однако, не изучается в рамках школьного курса геометрии.

Задание. Докажите, что у любого прямоугольного треуг-ка с целыми длинами сторон все эти длины не могут быть нечетными числами.

Предположим, что такой треуг-к существует. Пусть его стороны равны a, b и c, и эти числа нечетны. Тогда должно выполняться уравнение:

не может быть верным, ведь его левая часть четна, а правая – нечетна. Поэтому пифагоров треуг-к с тремя нечетными сторонами существовать не может.

Обратная теорема Пифагора

По теореме Пифагора из того факта, что в треуг-ке есть прямой угол, следует следующее соотношение между длинами его сторон:

Оказывается, верно и обратное: если в произвольном треуг-ке одна сторона (очевидно, большая из них) равна сумме квадратов двух других сторон, то из этого следует, что такой треуг-к является прямоугольным.

Это утверждение называют обратной теоремой Пифагора. Докажем её. Пусть есть некоторый ∆АВС, для сторон которого выполняется равенство

Так как ∆А₁В₁С₁ прямоугольный, то для него справедлива теорема Пифагора. Найдем с ее помощью гипотенузу:

а именно это мы и доказываем.

Уточним разницу между собственно теоремой Пифагора и только что доказанной обратной ей теореме. В каждой теореме есть две ключевые части:

1) некоторое условие, которое описывает какое-то геометрическое построение;

2) вывод (или заключение), который делается для условия.

В самой теореме Пифагора в качестве условия описывается прямоугольный треугольник. Для него делается вывод – катеты, возведенные в квадрат, в сумме дадут квадрат гипотенузы.

В обратной же теореме условие и вывод меняются местами. В роли условия описывается треугольник, у которого большая сторона, возведенная во 2-ую степень, равна сумме двух других сторон, также возведенная в квадрат. Для этого описания делается вывод – такой треугольник обязательно должен быть прямоугольным.

Заметим, что не всякая обратная теорема является справедливой. Например, одна из простейших теорем гласит – если углы вертикальные, то они равны. Сформулируем обратную теорему – если углы равны, то они вертикальные. Понятно, что это неверное утверждение.

Задание. Выясните, является ли треуг-к прямоугольным, если его стороны имеют длины:

Решение. Здесь надо просто проверить, являются ли эти числа пифагоровыми тройками. Если являются, то соответствующий треуг-к окажется прямоугольным.

Задание. В ∆КМР проведена биссектриса МН. Её длина 12. КМ = 13 и КН = 5. Найдите МР.

Решение. Рассмотрим ∆МНК. Его стороны равны 5, 12 и 13. Но это одна из пифагоровых троек:

Отсюда следует, что треуг-к прямоугольный, причем МК – гипотенуза (гипотенуза – это длиннейшая сторона). Тогда ∠Н = 90°. Но это означает, что биссектриса МН ещё и высота. Но если в треугольнике одна линия одновременно и медиана, и высота, то это равнобедренный треуг-к, причем КР – его основание. Тогда

Формула Герона

Невозможно построить два треугольника с тремя одинаковыми сторонами. Это значит, что теоретически знания трех сторон треугольника достаточно, чтобы найти его площадь. Но как это сделать? Здесь может помочь формула Герона, которая выводится с помощью теоремы Пифагора.

Пусть стороны треуг-ка равны а, b и с, причем с не меньше, чем а и b. В любом треуг-ке есть хотя бы два острых угла, а тупой угол, если он есть, лежит против большей стороны. Это значит, что оба прилегающих кс угла – острые. Отсюда следует, что высота, опущенная нас, будет лежать внутри треуг-ка. Обозначим длину этой высоты как h. Пусть она разобьет сторону сна два отрезка длиной х и у:

По рисунку можно записать три уравнения:

Левая часть одинакова в обоих уравнениях, значит, равны и правые:

С учетом этого выразим h 2 :

Мы уже выразили высоту (точнее, ее квадрат) через длины сторон. Однако обычно в этой формуле производят замену и вводят число р, равное полупериметру треуг-ка, то есть

Площадь треуг-ка вычисляется по формуле:

Запоминать вывод формулы Герона не надо. Саму формулу всегда можно найти в любом справочнике по геометрии или в Интернете. Достаточно запомнить, что площадь любого треуг-ка можно вычислить, если известны все его стороны.

Задание. Стороны треуг-ка имеют длину 9, 7 и 8 см. Какова его площадь?

Решение. Пусть а = 9; b = 8; с = 7. Для использования формулы Герона сначала вычислим половину периметра треуг-ка:

Итак, сегодня мы узнали о теореме Пифагора. Она представляет собой соотношение, которое связывает катеты и гипотенузу в прямоугольном треуг-ке. Это соотношение помогает в исследованиях других фигур – квадратов, параллелограммов, трапеций. Также с его помощью выведена формула Герона, которая позволяет вычислять площадь треуг-ка, зная только длины его сторон.

Источник