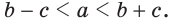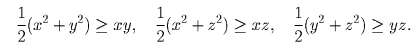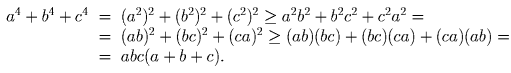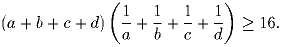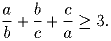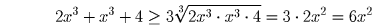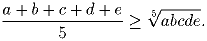Докажите что верно неравенство 37 35 меньше 12

Алгебра

Именная карта банка для детей
с крутым дизайном, +200 бонусов

Закажи свою собственную карту банка и получи бонусы

План урока:

Сравнение чисел

Если выбрать любые два различных числа, то одно из них обязательно окажется больше другого. Например, 15 больше, чем 12. Для записи этого факта используются специальные знаки. Символ « », означает «больше». Помимо них для сравнения чисел используются символы «⩾» (больше или равно) и «⩽» (меньше или равно).

Выражения, содержащие знаки сравнения, называются неравенствами. Иногда в учебной литературе может использоваться сокращение: нер-во.

Сравнивать натуральные числа очень легко, однако при сравнении отрицательных, дробных, иррациональных чисел могут возникнуть проблемы. Существует универсальный способ сравнивать числа между собой, основанный на использовании координатной прямой.

Можно заметить, что чем больше число, тем правее оно располагается на координатной прямой. Это правило действует для всех действительных чисел.

Отметим на прямой два числа, а и b, а также расстояние между ними (буква c):

b располагается правее а, а потому

Расстояние между ними равно c, причем с – положительное число. Очевидно, что

Перенося слагаемые через знак равенства, можно получить

Получается, что при вычитании из большего меньшего получается положительное число. Если же уменьшаемое меньше вычитаемого, то их разность – отрицательное число. На этом факте основан один из способов сравнения чисел. Чтобы узнать, какое из двух чисел больше, надо лишь вычесть их друг из друга и проанализировать знак получившейся разности.

Пример. Сравните дроби 29/35 и 33/40

Получили положительное число. Значит, уменьшаемое больше вычитаемого.

Свойства неравенств

Рассмотрим основные свойства числовых неравенств, которые в дальнейшем помогут нам решать некоторые задачи.

Докажем это. Если а >b, то тогда и разность (a –b) является положительным числом:

умножив части равенства на (– 1), получим:

Так как разность (b– a)оказалась равна отрицательному числу (– с), тоb

Для доказательства этого очевидного факта используем координатную прямую:

Ясно, что если b>a, то оно располагается правее. Аналогично и с располагается правее b, так как с >b. Видно, что тогда сбудет находиться правее а, то есть оно больше.

Свойство транзитивности позволяет использовать так называемые двойные неравенства. Например, нам надо указать, что 25 меньше 48, а 48 меньше 94. Это можно записать в виде одного неравенства:

Следующее свойство неравенств позволяет их складывать:

Докажем эту теорему. Найдем разность чисел (а + c) и (b + d):

(а + c) – (b + d) = а + с – b – d = (a– b) + (b– d)

Получили сумму двух слагаемых, (a– b) и (b– d). Каждое из них является отрицательным числом, так как a 25

В одном стоит знак «меньше», а в другом «больше», поэтому сразу их складывать нельзя. Сначала «перевернем» второе неравенство

Пример. Пете надо купить 2 килограмма бананов и пакет молока. Он точно знает, что пакет молока стоит в разных магазинах от 65 до 80 рублей, а стоимость килограмма бананов колеблется от 54 до 69 рублей. Помогите Пете оценить, сколько денег он потратит в магазине.

Решение. Обозначим буквой h стоимость килограмма бананов, а через k – цену пакета молока. Затраты Пети составят 2h + k, при этом можно написать следующие оценки:

Решение. Запишем очевидно верное неравенство

Добавим к нему число 11:

Число 11 больше 5, поэтому можно записать:

Пример. Докажите, что неравенство

n 2 – 8n + 19> 0

справедливо для любого n.

В левой части стоит квадратный трехчлен, попытаемся преобразовать его с помощью формулы квадрата суммы:

n 2 – 8n + 19 = n 2 – 2•4n + 19 = n 2 – 2•4n +16 – 16 + 19 =

= (n 2 – 2•4n + 4 2 ) – 16 + 19 = (n– 4) 2 + 3

Величина (n – 4) 2 является неотрицательным числом, поэтому сумма (n – 4) 2 + 3 никак не меньше трех, то есть положительна.

Иногда для доказательства числового неравенства можно определить знак разности выражений, стоящих в правой и левой части.

Пример. Докажите, что при любом значении переменных выполняется условие

Решение. Запишем разность выражений, стоящих в неравенстве, а потом преобразуем ее:

2ut – (u 2 + t 2 ) = 2ut – u 2 – t 2 = – (u 2 – 2ut + t 2 ) = – (u – t) 2

Разность получилась неположительной. Значит, между уменьшаемым и вычитаемым можно поставить знак «⩽»:

Полученное выражение означает, что удвоенное произведение двух чисел не превосходит сумму их квадратов. Этот факт мы используем при решении следующего задания.

Пример. Докажите, что

d 2 + s 2 + m 2 ⩾ds + dm + sm

Решение. В предыдущем примере мы установили, что сумма квадратов чисел больше или равна их двойному произведению, поэтому можно записать:

Сложим полученные неравенства:

(d 2 + s 2 ) + (s 2 + m 2 ) + (d 2 + m 2 ) ⩾2ds + 2sm + 2dm

2d 2 + 2s 2 + 2m 2 ⩾2ds + 2sm + 2dm

Осталось поделить на два это неравенство:

d 2 + s 2 + 2m 2 ⩾ds + sm + dm

Решение неравенств с одной переменной

Очевидно, что не все неравенства справедливы при любом значении входящих в них переменных. Так, нер-во

справедливо для х = 3 (так как 3 – 2 > 0), но несправедливо при х = 1. Такие выражения называют неравенствами с одной переменной. Его решением называют значение переменной, при подстановке которого получается справедливое числовое неравенство.

Так, 3 – это одно из решений для нер-ва

ведь при его подстановке получается справедливое числовое нер-во

Чтобы решить нер-во, надо указать сразу ВСЕ решения для него. Однако стоит заметить, что почти всегда нер-во, в отличие от уравнения, имеет бесконечное количество решений. Так, решением для нер-ва

является не только число 3, но также числа 4, 5, 6, 7, 8, и т.д. Более того, подойдут и дробные числа, например, 2,5; 2,6; 2,61 и т.д. Поэтому для указания решения нер-в используются особые математические объекты – числовые промежутки.

Отметим на координатной прямой числа а и b, а также точку с, лежащую между ними. Все числа, расположенные между ними, образуют множество, которое называют числовым промежутком:

Числовой промежуток обозначается скобками, в которых указаны его граничные точки: (а;b). В данном случае скобки круглые, это означает, что сами числа a и b НЕ входят в это множество. По этой причине концы промежутка на рисунке показаны незакрашенными точками, которые ещё называют «выколотыми».

Если некоторое число c располагается между числами a и b, то говорят, что с принадлежит промежутку (а; b). Записывается это так:

Естественно, что с принадлежит промежутку в том случае, если выполняется неравенство

Отметим на числовой прямой число 20 и всё множество решений этого нер-ва:

Решением нер-ва будет промежуток (20; + ∞)

Введем понятие равносильных неравенств:

Более сложные нер-ва можно свести к более простым, но равносильным им, с помощью нескольких приемов:

Эти способы основаны на свойствах нер-в и очень сильно напоминают способы преобразований уравнений. Рассмотрим их использование на примере.

Пример. Найдите решение неравенства с одной переменной

х + 10 > 18

Перенесем слагаемое 10 вправо, изменив его знак на противоположный:

Получили нер-во, решением которого является интервал (8; + ∞):

Пример. Решите нер-во

5у ⩾ 20

Решение. Поделим обе части на число 5. Оно положительное, а потому знак нер-ва не меняется:

Решением этого нер-ва будет интервал [4; + ∞)

Пример. Найдите значения переменной, при которых верна запись

–6z > 42

Решение. Поделим нер-во на (– 6). Так как это число отрицательное, то знак неравенства изменится на противоположный:

Решение. Перенесем слагаемое 26 вправо:

Теперь поделим на 12 правую и левую часть:

Для нер-ваk> 10 решением является промежуток

Пример. Решите нер-во

9(h + 2) + 21 10 (штриховка сверху) и х 0

Первый шаг – заменим знак «>» на «=»:

Получили уравнение. Вспомним правило: произведение множителей равно нулю, если хоть один из них равен нулю. Поэтому

х – 5 = 0 или х – 7 = 0 или 4 – 2х = 0

Решим каждое из трех полученных линейных уравнений:

Получили корни 2, 5 и 7. Отметим их на координатной прямой:

Эти точки разбивают числовую прямую на 4 промежутка:

В исходном неравенстве слева стоит произведение (х – 5)(х – 7)(4 – 2х). Определим его знак на каждом из этих 4 интервалов. Для этого достаточно взять одно число из интервала и подставить его в выражение:

(х – 5)(х – 7)(4 – 2х) = (0 – 5)(0 – 7)(4 – 2•0) = (– 5)•(– 7)•4 = 140

Получили число, большее нуля: 140 > 0

(х – 5)(х – 7)(4 – 2х) = (3 – 5)(3 – 7)(4 – 2•3) = (– 2)•(– 4)•(– 2) = – 16

Получили отрицательное число.

(х – 5)(х – 7)(4 – 2х) = (6 – 5)(6 – 7)(4 – 2•6) = 1•(– 1)•(– 8) = 8

Получили положительное число

(х – 5)(х – 7)(4 – 2х) = (8 – 5)(8 – 7)(4 – 2•8) = 3•1•(– 12) = – 36

Теперь поставим на числовой прямой знаки, соответствующие каждому интервалу:

Так как в исходном неравенстве стоял знак «>», то в ответ надо записать объединение тех интервалов, на которых левая часть принимает положительные значения.

В этом примере можно заметить, что знаки в интервалах чередовались. Так и должно происходить в том случае, если каждый из множителей в левой части является многочленом первой степени. Напомним, что многочлен 1-ой степени – это выражение вида ах + с, например:

Пример. Определите, при каких значениях переменной полином

х 2 – 8х + 12

принимает отрицательные значения.

Решение. По сути, нам надо решить нер-во

х 2 – 8х + 12 2 – 8х + 12 = 0

D = (– 8) 2 – 4•1•12 = 64 – 48 = 16

Зная х₁ и х₂, можем записать, что

х 2 – 8х + 12 = (х – х₁)(х – х₂) = (х – 2)(х – 6)

Перепишем исходное нер-во:

К нему уже можно применить метод интервалов (так как в левой части стоит произведение):

х – 2 = 0 или х – 6 = 0

Естественно, что мы получили те же корни, что и при решении квадратного уравнения выше. Отметим корни на прямой и определим значение трехчлена на каждом из полученных интервалов:

На промежутке (– ∞; 2) при х = 1 имеем (1 – 2)(1 – 6) = (– 1)•(– 5) = 5

Промежуток (2; 6): при х = 3 получаем (3 – 2)(3 – 6) = 1• (– 3) = – 3

На промежутке (6; + ∞) при х = 7 получается (7 – 2)(7 – 6) = 5•1 = 5

В итоге трехчлен отрицателен тогда, когда х принадлежит интервалу (2; 6).

Источник

Содержание:

Неравенство треугольника:

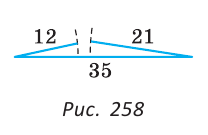
Опыт нам подсказывает, что путь из точки А в точку С по прямой АС короче, чем по ломаной ABC (рис. 255), т. е. АС 12+21 (рис. 258).

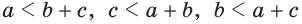
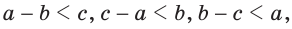
Замечание. Из неравенств треугольника следует, что то есть любая сторона треугольника больше разности двух других его сторон. Так, для стороны а справедливо

Пример:

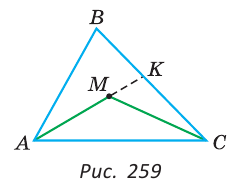
Внутри треугольника ABC взята точка М (рис. 259). Доказать, что периметр треугольника АМС меньше периметра треугольника ABC.

Решение:

Так как у треугольников ABC и АМС сторона АС — общая, то достаточно доказать, что AM + МС B (рис. 108, а).

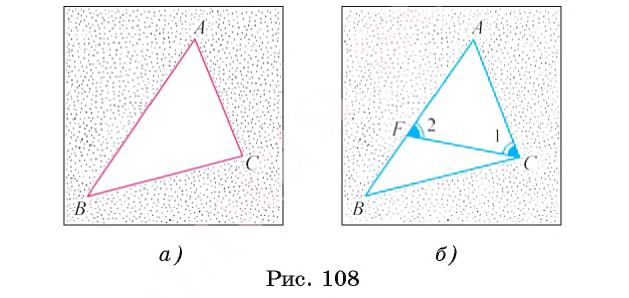
2) Отложим на стороне АВ отрезок АF, равный стороне AC (рис. 108, б).

3) Так как АF 1.

4) Угол 2 является внешним углом треугольника ВFС, следовательно, 2 > B.

5) Так как треугольник FАС является равнобедренным, то 1 = 2.

Таким образом, BСА > 1, 1 = 2 и 2 > B.

Отсюда получаем, что ВСА > B.

Теорема 2. В треугольнике против большего угла лежит большая сторона.

1) Пусть в треугольнике АBС С > B. Докажем, что АВ > АС (см. рис. 108, а). Доказательство проведем методом от противного.

2) Предположим, что это не так. Тогда: либо АВ = АС, либо АВ C.

В каждом из этих случаев получаем противоречие с условием: C > B. Таким образом, сделанное предположение неверно и, значит, АВ > АС.

Из данной теоремы следует утверждение: в прямоугольном треугольнике катет меньше гипотенузы.

Действительно, гипотенуза лежит против прямого угла, а катет — против острого. Поскольку прямой угол больше острого, то по теореме 2 получаем, что гипотенуза больше катета.

Теорема 3 (признак равнобедренного треугольника). Если два угла треугольника равны, то треугольник равнобедренный.

Пусть в треугольнике два угла равны. Тогда равны стороны, лежащие против этих углов. В самом деле, если предположить, что одна из указанных сторон больше другой, то по теореме 1 угол, лежащий против этой стороны, будет больше угла, лежащего против другой стороны, что противоречит условию равенства углов.

Значит, наше предположение неверно и в треугольнике две стороны равны, т. е. треугольник является равнобедренным.

Неравенство треугольника

Докажем, что длина каждой стороны треугольника меньше суммы длин двух других сторон.

Теорема 4. Длина каждой стороны треугольника меньше суммы длин двух других его сторон.

1) Пусть ABC — произвольный треугольник. Докажем, например, что выполняется неравенство АВ l, следовательно, верно неравенство АВF > 2.

4) Так как в треугольнике против большего угла лежит большая сторона (теорема 2), то АВ

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Докажите что верно неравенство 37 35 меньше 12

Задача 17:

Докажите, что 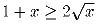при x ≥ 0.

Решение:

.

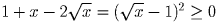
Задача 18:

Докажите, что x + 1/x ≥ 2 при x > 0.

Решение:

, ч.т.д.

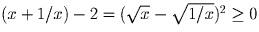
Задача 19:

Докажите, что (x² + y²)/2 ≥ xy при любых x и y.

Решение:

Перегруппировав члены, получаем (x – y)² ≥ 0.

Задача 20:

Докажите, что 2(x² + y²) ≥ (x + y)² при любых x и y.

Решение:

Перегруппировав члены, получаем (x – y)² ≥ 0.

Задача 21:

Докажите, что 1/x + 1/y ≥ 4/(x + y) при x,y > 0.

Решение:

Приводим к общему знаменателю и получаем (x – y)² ≥ 0.

Задача 22:

Докажите, что x² + y² + z² ≥ xy + yz + zx при любых x, y, z.

Решение:

Запишем три неравенства:

Сложив их, мы и получим требуемое неравенство.

Задача 23:

a, b, c ≥ 0. Докажите, что (a + b)(a + c)(b + c) ≥ 8abc.

Решение:

Надо перемножить три неравенства: , , .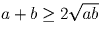

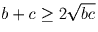
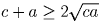
Задача 24:

a, b, c ≥ 0. Докажите, что .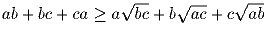

Решение:

.

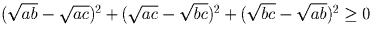
Задача 25:

Докажите, что x² + y² + 1 ≥ xy + x + y при любых x и y.

Решение:

x² + y² + 1 – xy – x – y = ((x – y)² + (x – 1)² + (y – 1)²)/2 ≥ 0.

Задача 26:

Докажите, что при любых a, b, c имеет место неравенство: a 4 + b 4 + c 4 ≥ abc(a + b + c).

Решение:

Воспользуемся неравенством x² + y² + z² ≥ xy + yz + zx, причем дважды:

Задача 27:

Докажите, что x 4 + y 4 + 8 ≥ 8xy при любых x и y.

Решение:

.

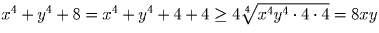
Задача 28:

a, b, c, d – положительные числа. Докажите, что

Решение:

; . Осталось лишь перемножить неравенства.

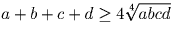
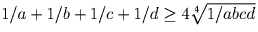
Задача 29:

a, b, c – положительные числа. Докажите, что

Решение:

.

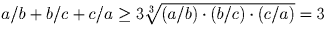
Задача 30:

Докажите, что при x ≥ 0 имеет место неравенство 3x³ – 6x² + 4 ≥ 0.

Решение:

Докажем, что 3x³ + 4 ≥ 6x². Но 3x³ + 4 = 2x³ + x³ + 4. Применяя неравенство Коши, получаем

Задача 31:

Докажите, что при a, b, c > 0 имеет место неравенство .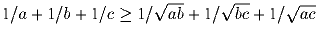

Задача 32:

Докажите, что при a, b, c > 0 имеет место неравенство ab/c + ac/b + bc/a ≥ a + b + c.

Задача 33:

Докажите, что при a, b, c ≥ 0 имеет место неравенство ((a + b + c)/3)² ≥ (ab + bc + ca)/3.

Задача 34:

Докажите, что при a, b, c ≥ 0 имеет место неравенство (ab + bc + ca)² ≥ 3abc(a + b + c).

Задача 35:

Сумма трех положительных чисел равна шести. Докажите, что сумма их квадратов не меньше 12.

Задача 36:

Докажите, что при x ≥ 0 имеет место неравенство .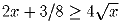

Задача 37:

Сумма двух неотрицательных чисел равна 10. Какое максимальное и какое минимальное значение может принимать сумма их квадратов?

Задача 38:

Докажите неравенство Коши для пяти чисел, т.е. докажите, что при a, b, c, d, e ≥ 0 имеет место неравенство

Решение:

Указание. Докажите сначала неравенство Коши для восьми чисел, а затем воспользуйтесь той же идеей, что и при доказательстве неравенства Коши для трех чисел.

Источник