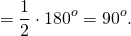Докажите что вписанный угол опирающийся на полуокружность прямой
Вписанный угол, опирающийся на диаметр
Вписанный угол, опирающийся на диаметр, обладает полезным свойством, вытекающим из теоремы о вписанном угле.
Свойство вписанного угла, опирающегося на диаметр
(следствие из теоремы о вписанном угле)
Вписанный угол, опирающийся на диаметр, прямой.
Дано:
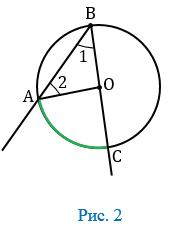
Так как AC- диаметр, то ∠AOC=180º.
∠AOC — центральный, ∠ABC — соответствующий ему вписанный угол.
Следовательно, по теореме о вписанном угле,
Что и требовалось доказать.
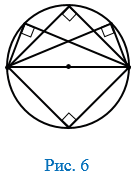
Из этого следует, например, что если центр описанной окружности лежит на стороне треугольника, то угол напротив этой стороны — прямой.
Если центр описанной окружности лежит на диагонали четырехугольника, то угол напротив этой диагонали — прямой.
Другой вариант формулировки следствия:
Диаметр виден из любой точки окружности под углом 90º.
Если вписанный угол связать с дугой, то следствие из теоремы о вписанном угле звучит так:
Вписанный угол, опирающийся на полуокружность — прямой.
Вписанный угол окружности
Вписанный угол окружности — это угол, образованный двумя хордами, исходящими из одной точки, то есть вписанным углом называется угол, вершина которого лежит на окружности.
Угол ABC — вписанный угол. ∠ABC опирается на дугу AC, заключённую между его сторонами.
Теорема о вписанном угле
Теорема:
Вписанный угол измеряется половиной дуги, на которую он опирается.
Это следует понимать так: вписанный угол содержит в два раза меньше градусов, чем дуга, на которую он опирается:
| ∠ABC = | 1 |  AC. |
| 2 |
При доказательстве этой теоремы следует рассмотреть три возможных случая расположения вписанного угла относительно центра окружности.
Первый случай. Сторона вписанного угла проходит через центр окружности.
Соединим точку A с центром круга (точкой O). Получим равнобедренный треугольник AOB, в котором AO = OB, как радиусы одной окружности. Следовательно, ∠A = ∠B, как углы при основании равнобедренного треугольника.
Так как ∠AOC — внешний угол равнобедренного треугольника, то:
а так как углы A и B равны, то
Но ∠AOC — центральный угол, значит ∠AOC = AC, следовательно ∠B измеряется половиной дуги AC:
| ∠ABC = ∠B = | 1 | AC. |
| 2 |
Второй случай. Центр окружности лежит между сторонами вписанного угла.
Проведём диаметр BD. Угол ABC разбился на два угла: ∠1 и ∠2.
Точка D разделяет дугу AC на две дуги: AD и DC. По доказательству, рассмотренному в первом случае:
| ∠1 = | 1 | AD и ∠2 = | 1 | DC. |
| 2 | 2 |
Следовательно, весь угол ABC будет измеряться половиной дуги AC:
| ∠1 + ∠2 = | 1 | AD + | 1 | DC |
| 2 | 2 |
| ∠ABC = | 1 | AC. |
| 2 |
Третий случай. Центр окружности лежит вне вписанного угла.
Проведём диаметр BD.
| ∠ABC = | 1 | AC. |
| 2 |
Следствия из теоремы
1. Все вписанные углы, опирающиеся на одну и ту же дугу, равны между собой, так как они измеряются половиной одной и той же дуги.
2. Вписанный угол, опирающийся на диаметр, — прямой, так как он опирается на половину окружности.
Половина окружности содержит 180°, значит, угол, опирающийся на диаметр, содержит 90°.
Теорема о вписанном угле
На рисунке 1 угол ВАС вписанный, дуга ВLС расположена внутри этого угла. В таком случае говорят, что вписанный угол АВС опирается на дугу ВLC.
Теорема
| Вписанный угол измеряется половиной дуги, на которую он опирается. |
Доказательство
Доказать: 
АВС = 
АС.
Доказательство:
Луч ВО совпадает с одной из сторон угла АВС.
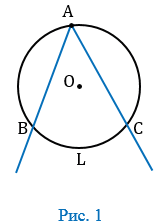
Пусть ВО совпадает с ВС (Рис. 2).
В данном случае дуга АС меньше полуокружности, следовательно, АОС =АС (т.к. АОС — центральный угол, причем он меньше полуокружности, поэтому градусная мера центрального угла равна градусной мере дуги, на которую он опирается).
Луч ВО делит угол АВС на два угла.
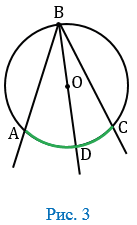
В данном случае луч ВО пересекает дугу АС в некоторой точке D (Рис. 3).
Точка D разделят дугу АС на две дуги: АD и DС, поэтому АС = АD + DС.
Луч ВD разделяет угол АВС на два угла, поэтому АВС = АВD + DВС.
По доказанному в 1 случае АВD = АD и DВС = DС. Складывая эти равенства, получаем: АВD + DВС = АD + DС или АВD + DВС = (АD + DС). Следовательно, АВС = АС.
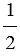
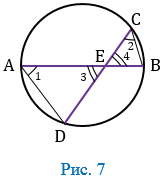
Луч ВО не делит угол АВС на два угла и не совпадает со стороной этого угла.
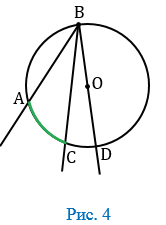
В данном случае луч ВС пересекает дугу АD в точке С (Рис. 4).
Луч ВС разделяет угол АВD на два угла, поэтому АВD = АВC + CВD, откуда АВC = АВD — CВD.
Теорема доказана.
Следствия из теоремы о вписанном угле
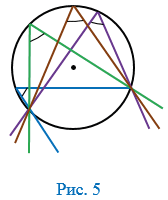
| 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны (Рис. 5). |
Теорема
| Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. |
Доказательство
Доказать: АЕ
ВЕ = СЕDЕ.
Доказательство:
В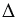 
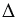
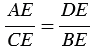
АDЕ и СВЕ: 1 = 2, т.к. они вписанные и опираются на одну и ту же дугу ВD (смотри следствие 1 из теоремы о вписанном угле), 3 = 4 как вертикальные углы, следовательно, треугольники АDЕ и СВЕ подобны (по 1 признаку подобия треугольников). В подобных треугольниках сходственные стороны пропорциональны, поэтому 
, откуда АЕВЕ = СЕDЕ. Теорема доказана.
Теорема
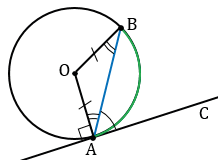
| Угол между касательной и хордой, проведенной в точку касания, равен половине дуги, стягиваемой этой хордой. |
Доказательство
Доказать: ВАС = АВ.
Доказательство:
Поделись с друзьями в социальных сетях:
Центральные и вписанные углы
Центральный угол и вписанный угол
Окружность — замкнутая линия, все точки которой равноудалены от ее центра.
Определение центрального угла:
Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.
На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF
Определение вписанного угла:
Вписанный угол — это угол, вершина которого лежит на окружности.
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу, что и вписанный угол.
На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC
Свойства центральных и вписанных углов
Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.
Угол AOC и угол ABC, вписанный в окружность, опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.
ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.
ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.
Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:
На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.
Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.
Хорда — отрезок, соединяющий две точки на окружности.
AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.
ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.
Примеры решения задач
Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.
Как решаем: окружность 360° − ⌒AC − ⌒CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ ⌒AB = 40°
Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.
Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ ⌒AC = 140/2 = 70°
Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?
⌒СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от ⌒CB = 72° / 2 = 36°
Углы, связанные с окружностью
Вписанные и центральные углы
Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
