Докажите и проиллюстрируйте графически что для двух взаимодополнительных событий энтропия
М Вернер Основы кодирования
4.2. Совместная и условная энтропия
После рассмотрения отдельных пар событий в предыдущем разделе, перейдем к средним оценкам источника. На рис. 4.2 показана исходная ситуация.
Рис. 4.2. Два связанных дискретных источника.
Совместная энтропия двух источников определяется как математическое ожидание информации всех пар событий.
Совместная энтропия двух дискретных источников без памяти X и Y
Замечание. Здесь подразумевается, что рассматриваются все, пары совместных событий, то есть
Усредняя условные информации всех пар событий, получим условную энтропию.
Таблица 4.1. Оценка совместной вероятности пар символов и вероятность отдельных символов и
Условная энтропия двух дискретных источников без памяти X и У
Пример: Связанные источники.
Сейчас самое время подробно разобрать числовой пример, наглядно поясняющий приведенные выше определения и формулы. Для этой цели была подобрана задача, методика решения которой может непосредственно использоваться на практике.
Пусть мы имеем выборку 100000 нар совместных событий дискретных источников X и У и алфавит каждого источника содержит четыре события. Пусть пара встретилась 10000 раз. Тогда оценка вероятности пары равна 10000/10000 = 0,1.
Теперь, когда нам известны все вероятности, необходимые для подсчета энтропии, определим:
1. Энтропии источников, X и Y ;
2. Совместную энтропию источников;
3. Обе условные энтропии;
Для контроля мы также вычислим:
4. Условные вероятности ;
5. Определим условную энтропию
Замечание. Для простоты проведем расчеты с точностью до 4 знаков после, запятой.
3. Без длинных вычислений из (4.16) получаем
Таблица 4.2. Условная вероятность
4. В таблице 4.2 приведены условные вероятности, подсчитанные исходя из таблицы 4.1. Заметим, что при этом мы получили так называемую стохастическую матрицу. Сумма условных вероятностей для каждой строки равна 1.
4.3. Выводы
Все приведенные в предыдущих разделах рассуждения в математической форме сведены в табл. 4.3. Напомним, что основной идеей теории информации является представление информации источника как меры неопределенности. Эта неопределенность раскрывается посредством экспериментов со случайными событиями из алфавита этого источника. Такой подход поясняют три столбца таблицы.
Таблица 4.3. Дискретные источники без памяти X и Y с символами и
Так как информация исходит из случайности событий, в первом столбце вводится понятие вероятности событий и совместной вероятности пары событий как основополагающих величин. Для пары событий вводится также понятие условной вероятности. Во втором столбце дается определение информации события и пары событий, а также условной и взаимной информации. И, наконец, в третьем столбце, вводится понятие энтропии как меры неопределенности источника.
Энтропия источника, совместная и условная энтропии двух источников трактуются как математические ожидания соответствующих информации событий. Условная вероятность это вероятность одного события при условии, что другое событие уже произошло, но этому, понятия условной информации и условной энтропии вполне естественно выводятся из условной вероятности.
Взаимная информация не имеет аналога в теории вероятности. Это совершенно новое понятие теории информации, играющее центральную роль в информационной технике. Взаимная информация связывает понятие канала с возможностью передачи информации по нему, т.е. с его пропускной способностью. Это понятие будет подробно рассмотрено в 7 главе этой книги.
Глава 5. Стационарные дискретные источники с памятью
5.1. Энтропия
Сигналы аналоговых источников информации ограничены по полосе, поэтому коррелированы во времени. Примером может служить аналоговый речевой сигнал в телефонной линии. После оцифровки, аналоговый источник превращается в дискретный и. например, после квантования сигнала на 256 уровней, мы получаем последовательнось 8-ми битовых двоичных целых чисел от 0 до 255. Как видно из рис. 5.1, значение двух соседних чисел близки друг к другу, т.к. телефонный сигнал передается в узкой полосе частот. Из-за временной связи соседних отсчетов, то есть памяти отсчета, его неопределенность (информация) снижается по сравнению с аналоговым источником без памяти, поэтому основной задачей методов сжатия, особенно при передаче видеосигналов, является снижение избыточности.
Рис. 5.1. Непрерывный сигнал.
Возникает вопрос о том, каким образом определить энтропию дискретного источника с памятью. Начнем с постановки задачи.
Определение 5.1.2. Дискретный источник является стационарным, если совместные вероятности последовательностей событий не зависят от выбора начальной точки отсчета времени.
Замечание. Независимость наблюдений от, точки отсчета означает, что мы можем начинать выборку с любого момента времени, то есть статистика не зависит от времени начала наблюдений.
Подход 1. Совместная энтропия.
Совместная энтропия двух источников х 1 и x 2 с одинаковыми алфавитами и одинаковыми распределениями вероятностей событий определяется как
Распространим это определение на L последовательных источников X i и найдем энтропию источника X L как
где вектор и суммирование производится по всем
Подход 2. Условная энтропия.
Хотя в левых частях равенств (5.3) и (5.4) мы уже использовали одинаковое обозначение энтропии отдельного события, этот факт предстоит доказать. Проведем это доказательство за 4 тага.
1. не возрастает с ростом длины блока L ;
3. Н L (Х) не возрастает с ростом длины блока L ;
4. Энтропия стационарного дискретного источника
1. Из определения энтропии, как меры неопределенности источника, непосредственно следует, что возрастание числа ограничений не может повлечь за собой рост неопределенности, а следовательно и энтропии.
2. Из «правила цепочки» для совместной энтропии следует
Так как энтропия всегда неотрицательна и имеет место неравенство
откуда следует нижняя оценка 2.
3. Из (5.5) прежде всего следует разложение
Используя уже известное соотношение (5.5). получаем неравенство
После подстановки получаем утверждение 3.
4. Утверждения 1.. 2. и ограничение устанавливают существование предела. Используя далее «правило цепочки», получаем
Согласно утверждению 1., условная энтропия в правой части равенства не возрастает, поэтому справедлива оценка
Устремляя j к бесконечности, получим
5.2. Теорема кодирования источников 2
Теперь мы можем дополнить теорию информации еще одной теоремой. Оказывается, что объединяя события источника в блоки длины L и кодируя эти блоки, средняя длина кодового слова на событие может достигнуть энтропию источника при как угодно близко. При этом намять источника полностью учитывается.
Теорема 5.2.1. Теорема кодирования стационарного дискретного источника с энтропией
Для блока длины L существует D-ичный префиксный код, в котором средняя длина кодового слова на одно событие п удовлетворяет неравенству
Теорема (5.14) не нуждается в специальном доказательстве. Если мы рассматриваем блоки длины L как новые независимые события с энтропией, равной и применяем теорему кодирования источников 1, то мы имеем
5.3. Конечные цепи Маркова
В этом и последующих параграфах будет рассматриваться специальная форма дискретных источников с памятью марковские источники. Их описание сходно с марковскими цепями, которые нашли разнообразное применение в других областях науки и техники. Так, на основе марковских цепей строятся модели распознавания речи, модели передачи по телефонным коммутируемым каналам. Цепи Маркова* используются при исследовании моделей сетей связи (каналы Гильберта-Элиота) и в теории управления транспортными потоками. Значение цепей Маркова основывается не только на их полном математическом описании, но также на том факте, что с их помощью можно составить математическую модель многих процессов, наиболее близкую к практике.
* Л. А. Марков (1856-1922) выдающийся русский математик. Прим. перев.
5.3.1. Дискретные во времени цепи Маркова
В этом разделе шаг за шагом вводится понятие конечных дискретных во времени марковских цепей. Мы наглядно поясним это понятие на простейшем примере «случайных блужданий».
Пример: Случайные блуждания студента:
Р («случайные блуждения» приведут к состоянию S 1 в момент времени п — 7).
Рис. 5.2. Случайные блуждания студента.
Исходным пунктом для описания марковской цени является множество состояний
Для того, чтобы полностью определить цепь Маркова, нам остается задать метод подсчета вероятностей для любого момента времени п. Из определения вероятности имеем
Особое значение имеет распределение вероятностей в начале наблюдения, т.е. начальные условия
Смена состояний описывается переходными, вероятностями
Эти переходные вероятности обладают следующими свойствами:
1. Одно из состояний в момент времени п всегда достигается при любом S i в момент п 1
При преобразовании (5.30) в (5.26), мы предполагаем
Последнее равенство характеризует марковский процесс.
Определение 5.3.1. Марковским процессом называется процесс, в котором прошлое не оказывает влияния на будущее, если настоящее известно.
Применение цепей Маркова сильно упрощается, когда они гомогенны, стационарны и регулярны. Рассмотрим эти три понятия.
Определение 5.3.2. Цепь Маркова гомогенна, если переходные вероятности между состояниями не зависят от выбора временной точки отсчета.
Таким образом, переходные вероятности зависят только от разности времен отсчетов /.
Это равенство может быть представлено в виде суммы покомпонентных произведений векторов-строк на векторы-столбцы. Записав переходные вероятности в виде матрицы, получим уравнение (5.33) в матричной форме
Этот процесс может быть начат с первого шага с помощью матрицы переходных вероятностей
Заметим, что матрица П стохастическая матрица с суммой вероятностей строк равной 1.
Теорема 5.3.1. Гомогенная цепь Маркова полностью характеризуется матрицей переходных вероятностей и исходным распределением состояний.
Энтропия объединения
Объединением называется совокупность двух и более взаимозависимых ансамблей дискретных случайных переменных.
Рассмотрим объединение, состоящее из двух ансамблей X и Y, например из двух дискретных измеряемых величин, связанных между собой вероятностными зависимостями. Объединение ансамблей характеризуется матрицей P(X, Y) вероятностей P(xi, yi) всех возможных комбинаций состояний 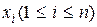
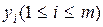
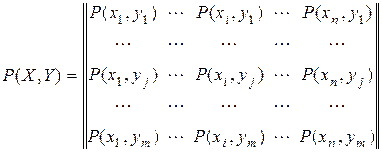
Cуммируя столбцы и строки матрицы (2.16), получим 
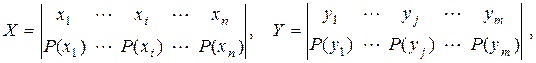
где 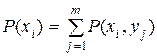
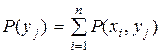
Вероятности P(xi, yj) совместной реализации взаимозависимых состояний xi и yi можно выразить через условные вероятности P(xi /yj) или P(yj /xi) в соответствии с тем, какие состояния принять за причину, а какие – за следствие.
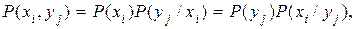
где P(xi /yj) – вероятность реализации состояний xi ансамбля X при условии, что реализовалось состояние yj ансамбля Y; P(yj / xi) – вероятность реализации состояний yj ансамбля Y при условии, что реализовалось состояние xi ансамбля X.
Тогда выражение для энтропии объединения в соответствии с (2.14) принимает вид:
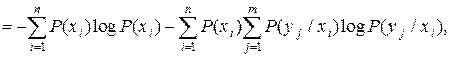
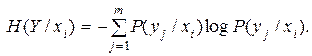
При усреднении по всем состояниям ансамбля X получаем среднюю неопределенность, приходящуюся на одно состояние ансамбля Y при известных состояниях ансамбля X:
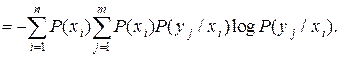
Величину H(Y/X) называют полной условной или просто условной энтропией ансамбля Y по отношению к ансамблю X.
Подставляя (2.21) в (2.19), получаем
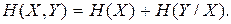
Выражая 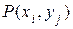
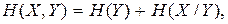
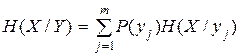
и 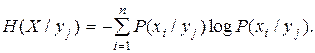
Таким образом, энтропия объединения двух статистически связанных ансамблей X и Y равна безусловной энтропии одного ансамбля плюс условная энтропия другого относительно первого.
В случае статистической независимости ансамблей X и Y имеют
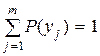
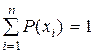
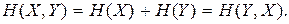
Свойства энтропии
2.4.1. Энтропия всегда неотрицательна, так как значения вероятностей выражаются дробными величинами, а их логарифмы – отрицательными величинами (2.14).
2.4.2. Энтропия равна нулю в том крайнем случае, когда одно событие равно единице, а все остальные – нулю. Это положение соответствует случаю, когда состояние источника полностью определено.
2.4.3. Энтропия имеет наибольшее значение при условии, когда все вероятности равны между собой (2.15).
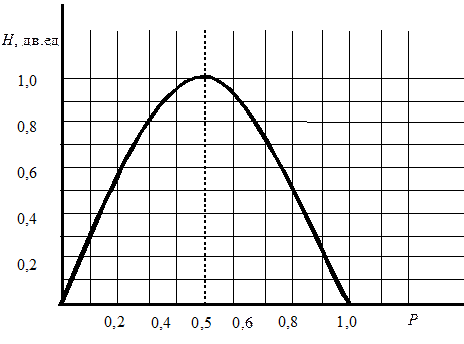
2.4.4. Энтропия источника Х с двумя состояниями х1 и х2 изменяется от нуля до единицы, достигая максимума при равенстве их вероятностей
График зависимости Н(Х) в функции Р:
приведен на рис. 2.1.
Отметим, что энтропия непрерывно зависит от вероятности отдельных состояний, что непосредственно вытекает из непрерывности функции -PlogP.
Рис. 2.1. Зависимость Н(Х) в функции Р
2.4.5. Энтропия объединения нескольких статистически независимых источников информации равна сумме энтропий исходных источников
2.4.6. Энтропия объединения двух статистически связанных ансамблей X и Y равна
2.4.7. Энтропия объединения любого числа зависимых ансамблей определяется из выражения
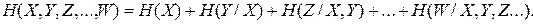
2.4.8. Энтропия не зависит от значений, принимаемых случайными величинами, а зависит только от вероятностей их появления (2.14).
2.4.9. Если события xi и yj статистически независимы при любых i и j, то
Таким образом, сведения о результатах выбора состояний из одного ансамбля не снижает неопределенности выбора состояний из другого ансамбля. Если имеет место однозначная связь в реализациях состояний 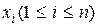
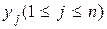
Действительно, условные вероятности P(xi/yj) и P(yj, xi) в этом случае принимают значения, равные нулю или единице. Поэтому все слагаемые, входящие в выражения (2.20) и (2.25), для частных условных энтропий равны нулю. Тогда в соответствии с (2.21) и (2.24) условные энтропии равны нулю.
Равенства (2.31) отражают факт отсутствия дополнительной неопределенности при выборе событий из второго ансамбля.
Уяснению соотношений между рассмотренными энтропиями дискретных источников информации (ансамблей) соответствует их графическое отображение (рис. 2.2).
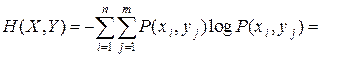
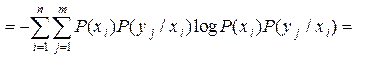
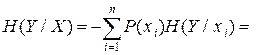
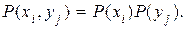
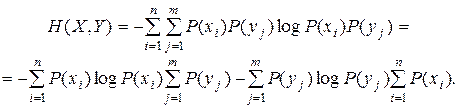
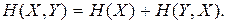
 X Y X Y
X Y X Y





 ()
()
 (2)
(2) Y
Y .
. . (3)
. (3) (4)
(4) . (5)
. (5)
 Y
Y . (6)
. (6) ( 17)
( 17) . (8)
. (8)
 .
.

 .
.
 = 0,1 × 0,01+0,3 × 0,98+0,4 × 0,01+0, × 2 × 0,01=0,301;
= 0,1 × 0,01+0,3 × 0,98+0,4 × 0,01+0, × 2 × 0,01=0,301; 0,1 × 0+0,3 × 0+0,4 × 0,98+0,2 × 0,02=0,396;
0,1 × 0+0,3 × 0+0,4 × 0,98+0,2 × 0,02=0,396; 0,1 × 0+0,3 × 0+0,4 × 0,01+0,2 × 0,97=0,198;
0,1 × 0+0,3 × 0+0,4 × 0,01+0,2 × 0,97=0,198; 0,105+0,301+0,396+0,198=1.
0,105+0,301+0,396+0,198=1. .
. бит/симв.
бит/симв.




 ,
, .
.
 ;
; ;
; .
. .
.

 (9)
(9) .
. , (20)
, (20) ;
;  .
.
 . (11)
. (11)
 Определим максимальное значение для энтропии:
Определим максимальное значение для энтропии:
 (12)
(12) . (13)
. (13)

 (14)
(14)
 , (15)
, (15)
 . (16)
. (16)