Докажите с помощью примеров и логических рассуждений что температура

§ 2. Логическая структура доказательства

§ 2. Логическая структура доказательства

Доказательство как особый логический способ обоснования истины имеет свое строение. Всякое доказательство включает: тезис, аргументы, демонстрацию. Каждый из этих элементов в логической структуре доказательства выполняет свои особые функции, поэтому ни один из них нельзя игнорировать при построении логически правильного доказательства. Допустим, что адвокату необходимо доказать алиби подсудимого. Адвокат, прежде всего, указывает, что в день и час совершения преступления его подзащитный находился в другом месте, то есть выделяет и формулирует тезис. Аргументами в подтверждение истинности данного тезиса будут процессуальные доказательст­ва. Демонстрация наглядно убеждает суд (присяжных заседателей) в логиче­ской связи между тезисом адвоката и установленными по делу фактами. Дадим логическую характеристику каждому из указанных элементов.

Тезис может быть сформулирован как в начале доказательства, так и в любой другой его момент. Тезис часто высказывается в форме категоричес­кого суждения, например: «Положение, которое я доказываю, состоит в следующем», «Вот мой тезис», «Передо мной стоит задача доказать», «Вот мое положение», «Я глубоко убежден, что. » и т.п. Нередко тезис формулируют и в форме вопроса, например: «Есть ли причинная связь между действиями обвиняемого и наступившими последствиями?».

Доказательства бывают простые и сложные. Главное их различие состоит в том, что в сложном доказательстве имеется основной тезис и частные тезисы.

В качестве аргументов при доказательстве тезиса может быть приведена любая истинная мысль, если только она связана с тезисом, обосновывает его. Основными видами аргументов являются: факты, законы, аксиомы, оп­ределения, документальные свидетельства и т. п. Рассмотрим их содержание более подробно.

Практика показывает, что факты никогда не говорят сами за себя. Фак­ты всегда объясняют люди. Вот почему один и тот же факт, взятый в различ­ных связях и отношениях, может быть объяснен по-разному. Но в одном и том же отношении, в одно и то же время факт должен объясняться однознач­но. Поэтому факты, прежде чем стать аргументами, должны быть правильно поняты. А для этого, необходимо подходить к ним диалектически, рассмат­ривать не изолированно, а во взаимной связи друг с другом, в единстве. Что­бы факты могли реализовать роль аргументов, нужно брать не отдельные факты, а всю совокупность относящихся к рассматриваемому вопросу фак­тов. Не следует произвольно ни выхватывать лишь нужные факты и забы­вать, не видеть других, нежелательных, ни брать у фактов лишь второстепен­ные стороны и не учитывать главных, существенных сторон. Всякая односторонность в отношении фактов ведет к непониманию их существа, осознанному или неосознанному их искажению.

Важным видом аргументов выступают законы науки. Ссылка на закон является веским аргументом. Авторитетность законов науки как аргументов связана с нашим пониманием того, что такое закон.

Но всякий закон имеет границы своего действия. Законы действуют в определенных условиях, с изменением которых может появиться другой за­кон. Поэтому при обосновании какого-либо положения при помощи зако­на надо знать, можно ли доказываемый тезис обосновать именно данным за­коном.

В судебном доказывании в качестве аргументов выступают юридические законы. Как известно, следствие и суд обосновывают свои выводы, прежде всего, на доказательственных фактах. Чтобы доказать, например, винов­ность подсудимого, необходимо привести доказательства (факты) по делу. Но в судебном доказывании факты сами по себе, взятые вне правовой нор­мы (юридического закона), ничего не обосновывают, из них нельзя сделать никакого вывода. Чтобы факты стали аргументами, необходимо установить их юридическое значение, а для этого факты должны быть сопоставлены с нормой права. Поэтому следствие и суд, обосновывая свой вывод, опираются одновременно и на факты действительности, и на правовую норму, статью закона.

При доказательстве истинности или ложности какого-либо положения в качестве аргументов часто приводятся определения понятий. Если выдвину­тое положение с необходимостью вытекает из приведенного в качестве аргу­мента определения понятия, то оно признается доказанным. Определение является результатом глубокого познания предметов, отраженных в данном понятии. Определение раскрывает содержание понятия, включает призна­ки, выражающие сущность предметов. Поэтому ссылка на определение мо­жет оказаться достаточной для признания истинности положения, подпадающего под данное определение. Определение в таких случаях принимается за истину, не требующую доказательства.

Однако необходимо учитывать, что не всякое определение может быть аргументом. Чтобы определение могло быть использовано для обоснования тезиса, оно должно быть истинным, правильным, общепринятым, утвердив­шимся в науке. Определение, которое оспаривается, требует своего уточне­ния, не может быть аргументом.

В судебном познании определения используются как основания доказа­тельства довольно широко. Обусловлено это тем, что многие определения правовых понятий даны в юридическом законе (в кодексах и других норма­тивных актах) и имеют общеобязательную силу. Ссылка на определение здесь есть ссылка на закон. Поэтому такие определения-аргументы являют­ся достаточными.

Определениями как аргументами пользуются всегда при доказательстве правильности юридической квалификации содеянного. Доказать положение о том, что действие обвиняемого квалифицировано правильно нельзя иначе, как сославшись на статью закона, описывающую признаки преступления, которое вменяется обвиняемому. Например, при доказательстве того, что действия обвиняемого представляют собой вымогательство, необходимо привести в качестве оснований доказательственные факты, собранные по делу, и статью уголовного кодекса, описывающую состав вымогательства.

Демонстрацией (или формой доказательства) называется способ логичес­кой связи тезиса с аргументами. Тезис и аргументы доказательства являются по своей логической форме суждениями. Выраженные в грамматических предложениях, они воспринимаются нами непосредственно: тезис и аргумен­ты можно увидеть, если они написаны, услышать, если они произнесены.

Доказательство является логической основой аргументации. Структура доказательства полностью входит в структуру аргументации, но не исчерпы­вает ее полностью. Это связано с тем, что знание воспринимается не только разумом, но и чувствами человека. Поэтому целесообразно говорить о логическом и психологическом компонентах структуры аргументации. В целом же различия между доказательством и аргументацией можно представить следующим образом:

Таковы общая характеристика структурных элементов доказательства и отличие его структуры от структуры аргументации. Для эффективного ис­пользования логического доказательства в специальной теории и практике необходимо иметь четкое представление о его видах.

Читайте также

3.2. Логическая структура высказываний

3.2. Логическая структура высказываний Различие между высказываниями и предложениями проявляется в их структуре. Грамматическая структура повествовательных предложений состоит из подлежащего, сказуемого и второстепенных членов предложения. В логике суждения также

7.2. Структура доказательства

7.2. Структура доказательства Во всяком доказательном рассуждении принято различать три части: тезис, аргументы и способ доказательства (или демонстрации).Тезисом называют то положение, которое требуется доказать. По своей логической форме тезис является заключением,

§ 3. Логическая структура понятия

§ 2. Логическая структура суждения

§ 1. Сущность и логическая структура вопроса

§ 1. Сущность и логическая структура гипотезы

§ 1. Сущность и логическая структура гипотезы Познание любого явления действительности, как известно, начинают с собирания и накопления отдельных фактов, относящихся к этому явлению. Фактов, которыми располагают в начале познания, всегда недостаточно, чтобы полностью и

5.2. Структура доказательства

5.2. Структура доказательства Опосредованное доказательство имеет определенную структуру, которая состоит из трех элементов:1. Тезис – это то, что доказывается (какое-либо суждение, высказывание, утверждение и т. п.).2. Аргументы, или основания – это то, чем доказывается

IV. ЛОГИЧЕСКАЯ СТРУКТУРА ДВУХ ОСНОВНЫХ ЗАКОНОВ МУЗЫКАЛbНОЙ ФОРМЫ

IV. ЛОГИЧЕСКАЯ СТРУКТУРА ДВУХ ОСНОВНЫХ ЗАКОНОВ МУЗЫКАЛbНОЙ ФОРМЫ 1Закон «золотого деления» как в искусстве вообще, так и в музыке может считаться вполне установленным и общепризнанным [160]. Не входя в конкретный анализ художественных произведений, построяемых по этому

Становление теоретического содержания и логическая структура «Манифеста Коммунистической партии»

Становление теоретического содержания и логическая структура «Манифеста Коммунистической партии» [490] За последние годы марксоведы и историки марксизма получили много новых данных относительно предыстории и истории создания Манифеста (находки и новые публикации

3. Система экономических категорий в связи с системой логических категорий. Логическая структура «Капитала»

3. Система экономических категорий в связи с системой логических категорий. Логическая структура «Капитала» Каждая отдельная наука оперирует своими специфическими категориями. Специфичность категорий каждой данной науки двояка: во-первых, все они отличаются друг от

2. Структура доказательства

2. Структура доказательства Любое доказательство независимо от его конкретного содержания, разного в различных сферах научной и практической деятельности, имеет одинаковую структуру. Оно заключает в себе два главных компонента: тезис и основания, которые находятся

2. Структура доказательства

2. Структура доказательства 1. В предыдущем примере вычлените структуру доказательства и выразите ее в схематической форме.2. О каких элементах структуры доказательства говорится в следующих высказываниях: «Речь имеет две части, ибо необходимо назвать предмет, о котором

Структура презентации и структура материала

Структура презентации и структура материала Если экран телевизора представляет образ какого-либо предмета, например скелета, то собственно структуру предмета мы понимаем как «структуру материала». Если же обратиться к структуре презентации, то она совершенно иная —

Источник

Знания за пределами математики и доказательной логики состоят из предположений. Предположения, составляющие математические знания, закрепляются доказательными рассуждениями и подкрепляются правдоподобными рассуждениями. Математическое доказательство является доказательным рассуждением, косвенные улики юриста, индуктивные доводы физика, статистические доводы экономиста относятся к правдоподобным рассуждениям. Доказательное рассуждение надежно, неоспоримо, окончательно. Правдоподобное рассуждение рискованно, спорно, условно.

Доказательное рассуждение имеет жесткие стандарты, кодифицированные и выясненные логикой, являющейся теорией доказательных рассуждений. Стандарты правдоподобных рассуждений текучи и нет никакой теории таких рассуждений, которая могла бы сравниться с доказательной логикой или обладала бы сравнимой с ней согласованностью.

Доказательные рассуждения. Все новые знания о мире связаны с правдоподобными рассуждениями.

Часто математические утверждения касаются бесконечного множества объектов, и перебрать эти объекты невозможно. Такой перебор можно заменить следующим методом рассуждения: если данное утверждение истинно в одном случае, то оно окажется истинным и в следующем за ним случае, а значит и во всех случаях. Такой метод рассуждения называется методом математической индукции.

Обобщение есть переход от рассмотрения данного множества предметов к рассмотрению большего множества, содержащего данное. Обобщение часто делается при переходе от одного предмета к целому классу, содержащему этот предмет.

Специализация есть переход от рассмотрения данного множества предметов к рассмотрению меньшего множества, содержащегося в данном. Специализация часто производится при переходе от целого класса предметов к одному предмету, содержащемуся в этом классе.

Аналогия. Две системы аналогичны, если они согласуются в ясно определенных отношениях соответствующих частей. Это отношение имеет ясный смысл, если отношения управляются одними и теми же законами.

Далее приводятся некоторые основные факты математической логики, которую еще называют формальной логикой. Формальной потому, что она позволяет проверить правильность рассуждений независимо от их содержания. Цепочки рассуждений в совершенно разных областях математики и других наук можно одинаково описать на языке логики и убедиться в их справедливости или ошибочности.

Высказывания и логические связки

Многие математические понятия удобно записывать в виде выражений, содержащих некоторые логические символы. Так, символ V, называемый квантором общности, используется вместо слов: «для любого», «для всех», «каково бы ни было. » и т.д., а символ

Отрицание — это высказывание, которое получается из данного высказывания А с помощью слова «не». Отрицание можно обозначать по-разному: .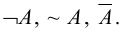

Простое добавление слова «не» к высказыванию чаще всего будет противоречить языковым нормам. Поэтому в конкретных случаях

требуется «перевод» полученного высказывания на русский язык. Пусть, например, А = «Завтра пойдет дождь». Что значит «Не (Завтра пойдет дождь)»: «Дождь пойдет не завтра», «Завтра пойдет не дождь» или «Завтра не пойдет дождь»? Здравый смысл подсказывает, что отрицанием высказывания А является третье предложение. Чтобы определить точно, дадим формальное определение отрицания.

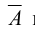
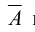
Отрицанием высказывания А называется такое высказывание, которое принимает значение / (ложно), если высказывание А истинно, и значение t (истинно), если высказывание А ложно. В нашем примере этому условию удовлетворяет только третье предложение. Итак, = «Завтра не пойдет дождь».

Дизъюнкция строится с помощью неисключающего «или». Таким образом, дизъюнкция A v В истинна, когда истинно, по крайней мере, одно из высказываний А и В или оба вместе. Другими словами, дизъюнкция ложна в том и только в том случае, когда оба высказывания ложны.

Импликация образуется из высказываний А и В с помощью слов «если. то. ». Получается высказывание вида «если А то В». Напомним, что математическая логика носит формальный характер, содержанием высказываний она не, занимается.

На примере импликации хорошо видна разница между обычным языком и языком логики. В обычном языке сложное предложение «если А, то В» предполагает между А и В отношение посылки и следствия, или же причины и обусловленного ею действия.

Импликация обозначается 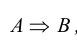, при этом говорят: «А влечет В» или «В при условии, что А», «В, если А», «А есть достаточное условие для В», «В есть необходимое условие для А».

Договорились, что импликация 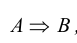ложна в том и только в том случае, когда высказывание А истинно, а высказывание В ложно. Такое определение подсказано здравым смыслом: разумно считать импликацию истинной, если В истинно, независимо от значения А; если оба участника импликации ложны, импликация, естественно, также истинна. В единственном случае, когда «предпосылка» импликации истинна, а «вывод» ложен, импликация считается ложной.

Эквиваленция образуется из высказываний А и В с помощью слов «. тогда и только тогда, когда. »:

Утверждение «А тогда и только тогда, когда В» не означает в логике, что составляющие высказывания А и В имеют одно и то же значение или один и тот же смысл.

Эквиваленция обозначается , Синонимы для эквиваленции: «если А, то В, и если В, то А», «А в том и только в том случае, когда «И есть необходимое и достаточное условие для В», «В есть необходимое и достаточное условие для А». Разумное определение эквиваленции: эквиваленция истинна в том и только в том случае, когда высказывания А и В имеют одинаковое значение истинности (либо оба истинны, либо оба ложны).

Новые высказывания (отрицание, дизъюнкция, конъюнкция, импликация и эквиваленция) образуются из существующих высказываний с помощью операций, или логических связок, имеющих те же названия.

В логике, как и в арифметике, операции делятся по старшинству. Это позволяет при записи сложных высказываний избегать большого количества скобок. Порядок выполнения операций таков: приоритет имеет отрицание, затем на одном уровне — дизъюнкция и конъюнкция, следующая связка — импликация и, наконец, самая последняя — эквиваленция.

Лекции по предметам:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

10. Краткий курс логики. Умозаключение

Умозаключение – это форма мышления, в которой из двух суждений, называемых посылками, вытекает третье – вывод.
1. Посылка: «Все люди – смертны».
2. Посылка: «Сократ – человек»
Ввод: «Сократ – смертный».

Умозаключения бывают непосредственные и опосредованные. Непосредственные умозаключения делаются из одной посылки, и являют собой уже известные нам действия над суждениями (обращения, превращения, противоставления предикату), а так же преобразование суждений по логическому квадрату. Опосредованные умозаключения делаются из нескольких посылок, о них мы и будем говорить в данной главе.

Существуют такие виды опосредованных умозаключений, их еще называют методами мышления:

Дедуктивный метод (Силлогизм) – метод при котором вывод о частном делается из общей совокупности вещей, о которых говориться в посылках. Проще говоря – вывод от общего к частному. К примеру:
1 посылка: «В группе 311 все студенты отличники».
2 посылка: «Этот ученик из 311 группы»
Вывод: «Этот ученик – отличник».
Еще пример:
1 посылка: «В этом ящике все шарики красные»
2 посылка: «Этот шарик их этого ящика»
Вывод: «Этот шарик красный».

Преимущество дедуктивного метода заключается в том, что при правильном использовании всегда дает точные выводы. Важно понимать, что все посылки входящие в силлогизм должны быть истинными, ложность хотя бы одной из них, ведет к ложности вывода. В принципе кто знаком с произведениями Артура Конана Дойля, должен был слышать о дедуктивном способе мышления. Его использовал Шерлок Холмс, в одном из произведений он приводит пример своего дедуктивного умозаключения Ватсону. Около жертвы преступления было найдена выкуренная сигарета, все решили, что сигарету выкурил полковник перед смертью. Однако у покойного были большие пышные усы, а сигарета была докуренная полностью. Шерлок Холм берется доказывать, что полковник не мог курить эту сигарету, так как он непременно бы подпалил бы себе усы. Вывод дедуктивный и верный, так как из общего правила вытекает частное.
Общее правило и первая посылка, выглядит так: «Все люди, которые носят большие, пышные усы не могут выкурить сигарету до конца»
Событие или вторая посылка выглядит так: «Полковник носил большие, пышные усы».
Вывод: «Полковник не мог выкурить сигарету до конца»

Индукция – метод, при котором вывод об общем делается из совокупности частных случаев. Проще говоря – это вывод от частного к общему. И пример тому:
1 посылка: «Первый, второй и третий студент – отличники».
2 посылка: «Эти студенты из 311 группы».
Вывод: «Все студенты в 311 группе – отличники».

1 посылка: ««Этот шарик красный».
2 посылка: «Этот шарик их этого ящика».
Вывод: «В этом ящике все шарики красные»

Некоторые учебники различают полную и не полную индукцию, полная индукция это когда перечисляются все элементы конечного множества вещей, о котором рассуждают. В нашем примере берутся все ученики и проверяют отличники они все или нет, а уже потом заключают обо всей группе. Не полная или частичная индукция – это наши примеры, в которых берутся только некоторые элементы конечного множества вещей. Само собой разумеется, не полное индуктивное заключения, на отмену от дедуктивного носит вероятностный, а не достоверный характер. Тем не менее, это не мешает пользоваться этим методом умозаключения в повседневной жизни. К примеру, мы, я уверен, слышали такое высказывание из уст женщины «Все мужчины – козлы», а ведь вывод об общем сделан из частного, по всем правилам индуктивного мышления.
1 посылка: «Первый человек – козел»
2 посылка: «Второй человек – козел».
3 посылка: «Эти люди – мужчины»
Вывод: «Все мужчины – козлы».

Чаще всего не полные индуктивные выводы – неверные. Их преимущество состоит в том, что они направленны на расширения знаний о предмете, могут указать на новые их свойства, в то время как индуктивный метод чаще всего направлен на выяснения уже известных фактов.

Я с некоторыми другими логиками выделяю еще такой вид умозаключения как Абдукция. Абдукция – это вид умозаключения, при котором на основе общего, делается вывод о причине частного, проще говоря – это вывод от общего к причине частного.
Я считаю, на отмену от общепринятого мнения, что именно этот вид умозаключений использовал на самом деле Шерлок Холмс, а так же другие реальные и не реальные детективы.
Чтобы понять, в чем заключается суть Абдукции, ее лучше рассматривать в сравнении с другими видами умозаключения.

А: «В этом ящике все шарики красные»
Б: «Этот шарик их этого ящика»
В: «Этот шарик красный».
Как видим с помощью дедукции – мы узнали результат, теперь переделаем рассуждения под индукцию:

Б: «Этот шарик их этого ящика»
В: «Этот шарик красный».
А: «В этом ящике все шарики красные»
Индукция, вывод от частного к общему открыл нам правило. Не трудно догадаться, что должен быть еще один вид умозаключений, который открывал бы нам случай, причину, ним и является Абдукция. Такой вид умозаключений будет выглядит так:

Существует, еще такой вид умозаключений как «вывод по аналогии». Это когда на основе свойств, признаков одного предмета делается вывод о свойствах другого. Формально это выглядит так:
Предмет А имеет свойство а, б, с, д.
Предмет В имеет свойсво а, б, с.
Вероятно В имеет и свойство д.
Так же как и неполная индукция умозаключения по аналогии носит вероятностный характер, но, не смотря на это, он широко используется, как в повседневной жизни, так и в науке.

Вернемся к дедукции. Мы предположили, что дедуктивный вид умозаключения имеет достоверный характер. Но, тем не менее, надо выделить некоторые правила простого силлогизм, чтобы это было действительно так. Итак, рассмотрим общие правила силлогизма.
1. В силлогизме должно быть только три термина или не должно быть термина, который употребляется в двух значениях. Если такой есть считается, что в силлогизме больше трех терминов, так как четвертый подразумевается. К примеру:
Движение – вечно.
Хождение в университет – это движение.
Хождение в университет – вечно.

Термин «Движение» употреблено в двух смыслах, в первом суждении, первой посылке оно обозначает всеобщее мировое изменения. А во второй механическое передвижение из одной точки в другую.

2. Средний термин должен быть распределён хотя бы в одной из посылок. Средний термин – это термин, который является базисом рассуждения и находиться в каждой из посылок.
Все хищные животные (+) – живые существа (-)
Все хомяки (+) – живые существа (-).
Все хомяки – хищные животные.
Средним термином является «живые существа». В обоих посылках его объем не распределён. В первой посылке оно не распределено, потому, что живые существа – это не только хищные животные. А во втором, потому, что живые существа – это не только все хомяки. Соответственно вывод в данном суждении не верный.
Еще один пример, который недавно прочел в одном журнале:
Все старые фильмы (+) – черно белые (-)
Все пингвины (+) – черно белые (-).
Пингвины – это старые фильмы.
Средний термин, то есть термин, который встречается в двух посылках – «черно белый». Как в первом, так и во втором суждении он не распределён, ведь черно белыми могут быть не только все старые фильмы или все пингвины.

4. Посылки силлогизма не могут быть только отрицательными. Вывод в таком силлогизме в лучшем случае будет вероятностным, но чаще всего его либо вообще невозможно сделать, либо он ложен.

5.Посылки силлогизма не могут быть только частными. Хотя бы одна посылка из силлогизма должна быть общая. В силлогизме, в котором две посылки частные сделать вывод не возможно.

6.Если в силлогизме одна посылка отрицательная, то и вывод будет отрицательным.

7.Если в силлогизме одна посылка частная, вывод из него следует так же только частный.

Силлогизм – самый распространённый вид умозаключений, потому, мы часто используем его в повседневной жизни и науке. Однако мы редко соблюдаем его логическую форму, и пользуемся сокращенными силлогизмами. К примеру: «Сократ смертный, потому, что все люди смертные». «Этот шарик красный, потому, что его взяли из ящика, в котором все шарики красные». «Железо – электропроводно, так как все металлы электропроводны» и т.д.

Различают такие виды сокращенного силлогизма:
Энтимема – это сокращенный силлогизм, в котором пропущена одна из посылок или вывод. Понятно, что из простого силлогизма можно вывести три энтимемы. К примеру, из простого силлогизма:
Все металлы – электропроводные.
Железо – это метал.
Железо – электропроводно.
Можно вывести три энтимемы:
1. «Железо – электропроводно так как оно является металлом». (пропущена первая посылка)
2. «Железо – электропроводно потому, что все металлы электропроводны». (пропущена вторая посылка)
3. «Все металлы электропроводны, а железо тоже метал». (пропущен вывод)

Следующий вид сокращенного умозаключения – Эпихейрема. Оно являет собой простой силлогизм, в которой две посылки – энтимемы.
Сначала сделаем из двух силлогизмов энтимемы:

Силлогизм №1.
Все то, что ограничивает человеческую свободу, делает его рабом.
Социальная необходимость ограничивает человеческую свободу
Социальная необходимость делает человека рабом.

Первая энтимема, если пропустить первую посылку будет выгладить так:
«Социальная необходимость делает человека рабом, потому, что ограничивает человеческую свободу.
Силлогизм №2.
Все действия, которые дают возможность существовать в социуме – являются социальной необходимостью.
Работа – это действие, которое дает возможность существовать в социуме.
Работа – это социальная необходимость.
Вторая энтимема, если пропустить первую посылку: «Работа – это социальная необходимость, так как является действием, которое дает возможность существовать в социуме».

Теперь сделаем силлогизм из двух энтимем, который и будет нашей эпихейремой:
Социальная необходимость делает человека рабом, потому, что ограничивает человеческую свободу.
Работа – это социальная необходимость, так как является действием, которое дает возможность существовать в социуме.
Работа – делает человека рабом.

Не исключено, что именно в таком порядке рассуждал Ницше говоря: «Мы видим, к чему сводится жизнь в обществе — каждый отдельный индивид приносится в жертву и служит орудием. Пройдите по улице, и вы увидите только «рабов». Куда? Зачем?»

Сорит – полисиллогизм, в котором пропущено суждение, связывающее два простых силлогизма, то есть вывод первого силлогизма, который стал первой посылкой второго, попросту упускается.
Все что развивает память и мышления – полезно.
Изучения наук – развивает память и мышления.
Логика – это наука.
Изучения логики – полезно.
Как видим суть силлогизма от того, что оно из полисиллогизма превратилось в сорит, не поменялась.

Источник