Доклад на тему что такое алгебра 7 класс
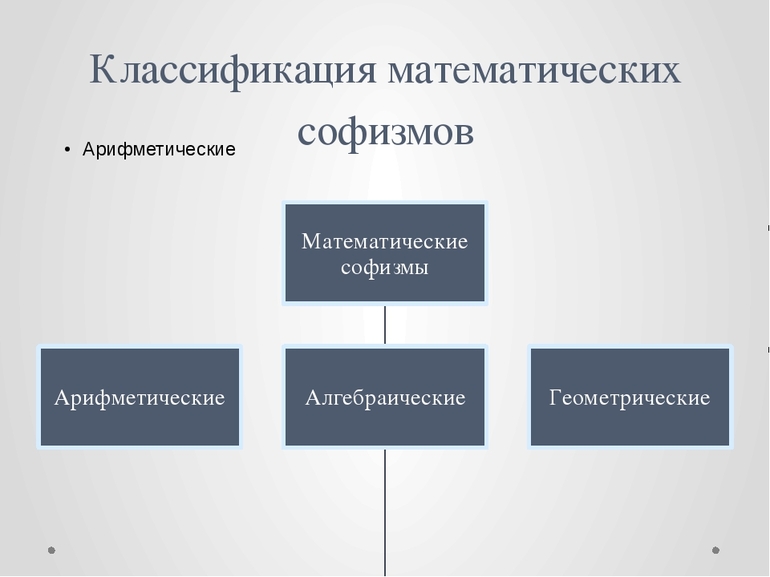
Классификация раздела
Алгебра является разделом математики. Она классифицируется на несколько видов:
Каждый из этих разделов решает определенные задачи. При этом наука не стоит на месте и продолжает развитие.
Древняя история
Информация об истории возникновения алгебры связывается с древними рукописями. В те времена появилось понятие о натуральных числах, с которыми можно было проводить арифметические операции. Такая потребность возникла в связи с проведением астрономических и других видов расчетов. Изучая историю алгебры, становится понятно, что ее зарождение произошло в античной Греции.
Происхождение науки связывается с мыслителем Диофантом. На сегодняшний день трудно сказать, кто придумал алгебру, но именно этим человеком были впервые введены буквенные обозначения чисел. На основании полученных сообщений известно, что Диофант знал о сокращении чисел и умел переносить члены из разных частей уравнения.
Информация об ученом содержится только в одном историческом труде, поэтому сказать точно, что математик создал алгебру, невозможно. К тому же этот источник дошел до нынешних времен не в полном объеме.
Продвижение на Восток
Достижения европейцев в области развития алгебры прервались после нашествий варварских племен. Кроме того, уменьшение к ней интереса произошло с открытием геометрии, которая стала считаться основным разделом математики. В этот период многие науки получили свое развитие на Востоке. Здесь продолжилось становление и алгебры. Поскольку все достижения Европы практически были забыты, создателем этой науки в мусульманском мире считается Ала-Хорезми. Произошло это после создания им трактата под названием «Учение об отношениях, перестановках и решениях». Некоторые ученые считают, что слово «алгебра» может вести свое начало от термина «алгоритм».
При этом существуют гипотезы, что мусульманский мир опирался в своих изучениях на европейские достижения. В некоторых их летописях присутствуют фамилии греческих последователей Диофанта, приводятся их высказывания относительно этой науки.
Вклад других стран
Основателем алгебры считается Ала-Хорезми, но особого развития она у арабов она получила. Однако именно они изобрели на своем языке арабские цифры, которые применяются в современном мире. Существенный вклад в развитие науки внесли представители и других стран. Кратко их достижения выражаются в следующем:
Таким образом, в развитии этого раздела принимали участие многие страны мира. Их исследовательские работы вносили общий вклад в становление алгебры.
Под конец XVI века эта часть математики снова возвращается в Европу, откуда она взяла свое начало. Этому способствовало купечество, разъезжающее по всему свету и знакомившееся с математикой. Дальнейший толчок произошел после распада феодальной системы. Страны, ставшие на капиталистический путь развития, уже не могли обойтись без алгебраических действий.
Алгебра относится к наиболее интересным наукам, которые изучаются учениками школ и студентами вузов. Учащиеся постоянно пишут рефераты и готовят доклады на различные темы, относящиеся к этому разделу математики. В дальнейшем они зачитывают свои работы на уроках.
История возникновения алгебры и ее развития
История возникновения алгебры уходит своими корнями в глубокую древность. Очевидно, ее появление было вызвано и непосредственно связано с первыми астрономическими и другими расчетами, так или иначе использующими натуральные числа и арифметические операции. История возникновения алгебры подтверждается подобными оригинальными записями, найденными среди образцов письменности самых ранних цивилизаций.
Содержимое разработки
История возникновения алгебры уходит своими корнями в глубокую древность. Очевидно, ее появление было вызвано и непосредственно связано с первыми астрономическими и другими расчетами, так или иначе использующими натуральные числа и арифметические операции. История возникновения алгебры подтверждается подобными оригинальными записями, найденными среди образцов письменности самых ранних цивилизаций. К примеру, египтяне и вавилоняне уже умели решать простейшие уравнения первой и второй степеней, квадратные уравнения. Но их вычисления носили строго практический характер. История возникновения алгебры, как теоретической науки, приводит нас в античную Грецию. Именно здесь в IV веке появилось первое сочинение, которое являлось непосредственным исследованием абстрактных алгебраических вопросов. Это был трактат мыслителя Диофанта. Здесь уже четко обозначены простейшие алгебраические аксиомы: правила знаков (минус на минус – плюс, и так далее), примеры достаточно сложных задач, исследование числовых степеней, решения вопросов, связанных с теорией чисел и так далее. К сожалению, это единственный труд, который дошел до нас из седых древних времен, да и то не в полном объеме.
Арабская математика С крушением античной цивилизации под натиском варварских народов теряются и многие ее достижения. В том числе и история алгебры прерывает свое развитие у европейских народов на целое тысячелетие. С VII века центром множества наук, а математики и медицины особенно, становится мусульманский Восток. Собственно, само слово «алгебра», как считается сегодня, происходит от названия трактата арабского ученого Ал-Хорезми «Аль-джабо-аль-мукабалла», что переводилось, как «учение об отношениях, перестановках и решениях». Интересно, что от самого имени этого математика некоторые ученые выводят этимологию слова «алгоритм». Как бы то ни было, но именно арабский мир на долгие столетия становится светочем науки. Вместе с тем восточные последователи, очевидно, опирались на некоторые греческие достижения. Во всяком случае, точно известно, что им были известны труды античных математиков. С одной стороны, мусульманам действительно принадлежит заслуга сохранения для мира античного алгебраического наследия, но вместе с тем, за несколько столетий они так и не внесли в развитие этой науки новых существенных открытий. Математика изучалась, но не совершенствовалась.
Математика и другие цивилизации Интересно, что история возникновения алгебры вовсе не ограничивается Европой и имеющей с ней связь арабской цивилизацией. Так, существенных результатов в этой науке достигли индийские математики. В частности, именно они ввели понятие «нуля», которое позже через арабский мир пришло в Европу и стало использоваться учеными. Китайцы совершенно независимо, еще на заре нашей эры, научились решать уравнения первой степени. Им были известны иррациональные и отрицательные числа.
Европа возвращает лидерство Прерванная история развития алгебры вновь начинает свой отсчет уже в Новое время. Первым сочинением после трактата Диофанта считается труд купца из Италии Леонардо, который познакомился с арифметикой и алгеброй, путешествуя по востоку. Постепенное разложение феодализма, а вместе с ним церковной схоластики и догматики, неторопливая поступь капитализма и стремление к территориальным открытиям привели к возрождению все научные отрасли на континенте. И уже спустя пару столетий Европа вновь становится передовым в научном и техническом плане регионом.
Класс: 7
Презентация к уроку
Ход урока
Мы с вами уже полугодие изучаем новый предмет – алгебра, но я не случайно не отвечала вам подробно на вопрос – Что же такое алгебра? Что она изучает? А делала я это потому, что вы были еще не готовы, не хватало ваших знаний. Сегодня этот момент наступил. На уроке мы постараемся разобраться что изучает алгебра, что лежит в ее основе, заглянем в историю создания предмета.
Откройте тетради, запишите число и тему:
Что изучает алгебра? (слайд №1)
С чего начнем? Наверное, с названия (слайд №2)
По многим названиям предметов сразу становиться ясно, чем занимается данная наука.
| Геометрия – гео-земля метро-мерять Биология – био– жизнь логос-учение География – гео-земля графо – пишу |
А слово “Алгебра” или “Аль-джебр” в переводе с арабского означает
Стало понятно чем занимается алгебра?
Наверное, наоборот, вводит в замешательство.
Вот так и в древней Испании, которая долгое время была под арабским владычеством и, слыша слово “алгебраист” решили, что это слово относится к костоправам или по нашему к хирургам и это недоразумение вошло в книгу
Сервантеса “Дон Кихот” там есть такой фрагмент, когда главный герой Дон Кихот был ранен в одном из поединков, то он просит своего верного друга Санчо Панса привести к нему срочно алгебриста.
Кто-то из вас уже читал или смотрел фильм по этой книге?
Т.е. перевод названия нашего предмета ничего не прояснил.
Что ж, пойдем другим путем.
Посмотрим, что же лежит в основе алгебры? Или другими словами, на чем стоит этот предмет? …
А стоит он на четырех больших китах. (слайд №4)
Давайте познакомимся с этими китами поближе. (Слайд №5)
у= 4х – 6 у = – 5х + 0,3 у = 6,5х
F(х)= 4х 3 +3х у = 6,5х 2
у= 7 – 3х+ ln у = х 3 f(х) = х 2 +х-4
y = sin3x
На этом слайде вы видите надписи. Что это? (Функции)
Запишите в тетрадь. Это кит-функция. (Слайд №6)
– Какими способами можно задать функцию?
– С какими функциями мы уже знакомы?
Это огромный раздел нашего предмета Алгебры.
А сейчас задание по вариантам от первого кита-функции (слайд №7)
| Построить графики следующих функций на одних осях координат: | |
| 1 вариант; | |
Самостоятельная работа на 5 минут в тетради. Затем проверить (слайд №8) и (слайд №9) причем, ответы с ошибками. Должны заметить, что в 1 варианте не подписаны оси координат, а во 2 вар. не подписаны графики и ошибки исправить по щелчку мышкой
Мы познакомились с китом – Функция (слайд №10)
А что вы видите на спине второго кита? (слайд №11)

Sin 2 2x – 3cos2x = 0
Конечно, это уравнения. Только некоторые из них нам хорошо знакомы, а с остальными нам предстоит знакомство на протяжении учебы. Запишите в тетрадь кит-уравнение. (слайд №12)
– Что такое уравнение?
– Что значит решить уравнение?
Оказывается, благодаря решению уравнений, мы получили название нашего предмета – алгебра.
(слайд №13) Впервые это слово прозвучало в книге ученого 1 века нашей эры Мухаммед Бен Мусса Аль-Хорезми (787 – около 850)
Откройте ваши учебники на стр. 16.
(Алгебра 7 класс под редакцией С.А. Теляковского)
Название у нее было очень странное (слайд №14)
“Краткая книга об исчислении аль-джабры и аль-мукабалы”
В ней рассказывалось о том, как решаются уравнения. Причем этими правилами мы пользуемся и теперь
Слово “аль-джабра” видимо понравилось ученым и оно дало название нашему предмету
Задание от этого кита (слайд №15)
(Самостоятельно 5 минут. Проверить ответы по щелчку)
РЕШИТЕ УРАВНЕНИЯ:
1) 2у(3у – 7) – (7 – 3у) = 0;
2) 
1) 7х(8х – 3) – (3 – 8х) = 0
2)
(слайд №16) Посмотрите на третьего кита.
Что вы видите на его спине (слайд №17)
Значит третий кит называется Тождество. Запишите в тетрадь.
– А что такое тождество?
Кит Тождество приготовил работу на желтым карточках
Задание от кита “Тождество”
Выполните тождественные преобразования и упростите выражение:
Задание от кита “Тождество”
Выполните тождественные преобразования и упростите выражение:
2) (1-2а)(14-а)+а(а 2 +51)-2(а 2 +21)
Задание от кита “Тождество”
Выполните тождественные преобразования и упростите выражение:
Задание от кита “Тождество”
Выполните тождественные преобразования и упростите выражение:
Мы познакомились с тремя китами. (Слайд №20) С тремя основными разделами алгебры, а это самый старый и уважаемый. Без него не могут обходиться другие киты никак. Это кит – … (число) (слайд №21)
Задание от кита “ЧИСЛО”
Выполните действия в 2-х примерах:
Задание от кита “ЧИСЛО”
Выполните действия в 2-х примерах:
От него вам задание на оранжевой карточке (слайд №22), но коль это уважаемый кит и его решение не терпит суеты – выполните его дома, а завтра на уроке мы проверим, кроме этого (слайд №23) на домашнее задание пойдут следующие номера: №241, №366, №778.
А сейчас посчитайте сколько плюсов вы заработали
– Сколько плюсов-такая и оценка за работу на уроке. (слайд №24)
Подведение итогов. Выставление оценок за урок.
Для следующего урока. (Слайд №25)
Доклад на тему Возникновение алгебры сообщение
Этот раздел науки возник еще в древние времена. Четыре тысячи лет назад люди могли решать непростые квадратные уравнения. В то время у греков был популярен один интересный подход к решению различных алгебраических задач. Из них большая часть решалась геометрическим путем. Это привело к замедлению процесса эволюции алгебры. Тогда отсутствовали особые системы обозначения, большинство многосложных формул обретало лишь словесное определение, все это приводило к замедлению эволюции науки.
Изучить этот отдел арифметики, в основе которой лежит алгебра, позволили исследования Диофанта. Он сумел ввести обозначения буквами. Новые величины он именовал «число». Также ввел обозначения степеням: вторую степень — «квадрат», третью — «куб», четвёртую — «квадрато-квадрат», пятую — «квадрато-куб», 6 — «кубо-куб». Еще он ввел символы для определения знака равенства, чисел со знаком отрицания и степеней. Математик для того, чтобы обнаружить рациональную точку, расположенной на какой-либо кривой, применял необычный на то время способ. Он либо проводил касательную в рациональную точку, либо проводил прямую линию сквозь несколько таких точек.
Леонардо Пизанский являлся первым человеком, у которого получилось ответить почти на все вопросы других математиков, он сыграл важную роль в развитии математики. Все труды он описал в книге ”Книга абака”. Там он описал решение разнообразных задач, линейных и квадратных уравнений. Все это было выполнено с необычайной на то время точностью и полнотой.
На сегодняшний день в ходе изучения такой науки, как алгебра, часто используются новейшие технологии. Многие компьютерные программы позволяют использовать ранее неизвестные приемы в решении определенных задач. Это способствует развитию дисциплины, помогает ей выйти на совершенно новый этап эволюции.
Вариант №2
Родина вычислительной науки
Указать место, являющиеся родиной математики и алгебры довольно трудно. Мудрецы различных цивилизаций практически одновременно стали выяснять всё больше и больше закономерностей и числовых правил. Индийские мудрецы, например, ввели такое понятие как “нуль”, которое используется и по сей день. А математики Древнего Китая в первые века нашей эры (не зависимо от мудрецов Древней Греции) практиковали решения уравнений первой степени. Им были известны также и отрицательные числа.
Угасание науки
Из-за многочисленных войн за территорию, наука прекратила своё развитие у некоторых государств на несколько веков. Именно с этого момента первенство в изучении алгебры и многих других наук переходит на мусульманский Восток. Но открытия восточных мудрецов не могли сравниться с теми, что были в древности. Поэтому учёными принято считать, что в этот период времени происходило изучение науки, но не её совершенствование. Но тем не менее арабские математики подготовили достаточно прочный фундамент для дальнейших открытий и продвижений алгебры.
Интересный факт: существует ложное предположения, что знаменитый Альфред Нобель не включил в список дисциплин своей премии алгебру, из-за измены его жены с математиком. Но это совсем не так! На самом деле он считал, что открытия в математических науках не оказывают никакой пользы человечеству и носят только теоретический характер.
Возникновение алгебры
Популярные темы сообщений
Кто такой Дмитрий Донской? Он – великий князь, добившийся независимости Московского княжества и расширивший её территорию до невиданных прежде размеров. При нём другие княжества (в первую очередь великое Владимирское, а также
Ворона – очень умная птица. В ее характере присутствует осторожность, терпение и наглость. Эта птица загадочна и неповторима. Вороны – крупные птицы отряда Воробьинообразные. Они относятся к роду Вороны семейства Врановые.
Всероссийская проверочная работа, это, конечно, не экзамен и бояться этого не стоит. ВПР проводятся исключительно для отслеживания уровня знаний в школах.
Реферат на тему: История появления алгебры как науки
Содержание:
Введение
Деление алгебры
В настоящее время, отчасти по педагогическим соображениям, отчасти в силу исторического развития этой науки, алгебра делится на низшую и высшую. К низшей алгебре относятся теория элементарных арифметических операций над алгебраическими выражениями, решение уравнений первой и второй степени, теория степеней и корней, теория логарифмов и комбинаторика. Высшая алгебра включает в себя теорию уравнений произвольных степеней, теорию исключений, теорию симметричных функций, теорию подстановок и, наконец, представление различных частных способов разделения корней уравнений, определения числа действительных или мнимых корней данного уравнения с числовыми коэффициентами и приближенных или аналитических (когда это возможно) уравнений произвольных степеней.
История алгебры
Происхождение термина «алгебра».
Происхождение самого слова «алгебра» не совсем ясно. По мнению большинства исследователей, слово «алгебра» происходит от названия работы арабского математика аль-Хорезми (от названия которого, по мнению большинства исследователей, происходит популярное слово «алгоритм») «аль-Джабр аль-мукабала», то есть «учение о перестановках, соотношениях и решениях», но некоторые авторы производят слово «алгебра» от имени математики ГЕБЕРА, но само существование такой математики подлежит сомнению.
Самые старые комбинации в алгебре
Первой дошедшей до нас работой, содержащей исследование алгебраических вопросов, является трактат Диофанта, жившего в середине IV века. В этом трактате мы находим, например, правило знаков (минус на минус дает плюс), изучение степеней чисел и решение многих неясных вопросов, которые в настоящее время относятся к теории чисел. Из 13 книг, составлявших полное собрание сочинений Диофанта, до нас дошло только 6, в которых решаются уже довольно сложные алгебраические задачи. Мы не знаем никаких других работ по алгебре в древности, кроме утраченной работы знаменитой дочери Теона, Ипатии.
Арабская алгебра
В Европе алгебра вновь появляется только в эпоху Возрождения, и то от арабов. Как арабы достигли истин, которые мы находим в их писаниях, дошедших до нас в большом количестве, неизвестно. Возможно, они были знакомы с трактатами греков или, как некоторые думают, получили свои знания из Индии. Сами арабы приписывали изобретение алгебры. Магомед ибн Муса, живший примерно в середине девятого века в царствование халифа Аль-Мамуна. Во всяком случае, греческие авторы были известны арабам, которые собирали древние труды по всем отраслям науки. Магомед Абульвафа переводил и комментировал труды Диофанта и других предшествовавших ему математиков (в X веке). Но ни он, ни другие арабские математики не привнесли в алгебру много своего. Они изучили его, но не улучшили.
Возрождение алгебры в Европе
Решение уравнений третьей и четвертой степени
Вскоре было найдено решение уравнений четвертой степени. Итальянский математик предложил задачу, решение которой по известным до того времени правилам было недостаточным и требовало умения решать биквадратичные уравнения. Большинство математиков считали эту проблему неразрешимой. Но Кардано предложил его своему ученику Луиджи Феррари, который не только решил задачу, но и нашел способ решения уравнений четвертой степени в целом, сведя их к уравнениям третьей степени. В работе Тартальи, напечатанной в 1546 году, мы также находим изложение метода решения не только уравнений первой и второй степени, но и кубических уравнений, и описан инцидент между автором и Кардано, описанный выше. Работа Бомбелли, опубликованная в 1572 году, интересна тем, что в ней рассматривается так называемый неприводимый случай кубического уравнения, который смутил Кардано, не сумевшего решить его с помощью своего правила, а также указывается на связь этого случая с классической задачей о трисекции угла. алгебра уравнения математической
Развитие алгебры в Европе
В Германии первая работа по алгебре принадлежит Христиану Рудольфу Яуэрскому и впервые появилась в 1524 году, а затем снова была опубликована Штифелем в 1571 году. Сами Штифель и Шейбл, независимо от итальянских математиков, разработали некоторые алгебраические вопросы.
В Англии первый трактат по алгебре принадлежит Роберту Рекорду, профессору математики и медицины в Кембридже. Его сочинение по алгебре называется «Точильный камень остроумия». Здесь впервые вводится знак равенства ( = ). Во Франции в 1558 году появилось первое сочинение по алгебре Пелетария; в Голландии в 1585 году Стевин не только представил уже известные ему исследования, но и внес некоторые усовершенствования в алгебру. Например, он обозначал неизвестное. Однако для обозначения неизвестного он использовал только цифры, обведенные по кругу. Итак, первое неизвестное (теперь обычно обозначаемое х) В его случае обозначалось обведенной единицей, второе-обведенной двойкой и так далее. Большие успехи были сделаны в алгебре после трудов Виеты, который первым рассмотрел общие свойства уравнений произвольных степеней и показал методы приближенного нахождения корней любых алгебраических уравнений. Он первым обозначил буквами величины, входящие в уравнения, и тем самым придал алгебре ту общность, которая является характерной чертой алгебраических исследований нового времени. Он также очень близко подошел к открытию биномиальной формулы, найденной позднее Ньютоном, и, наконец, в его трудах можно даже найти разложение отношения стороны квадрата, вписанного в окружность, к дуге окружности, выраженной в виде бесконечного произведения. Фламандец Альберт Жирар, или Жерар, чей трактат по алгебре появился в 1629 году, первым ввел в науку понятие мнимых величин. Англичанин Харриот показал, что каждое уравнение можно рассматривать как произведение некоторого числа факторов первого порядка, и ввел знаки > и
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.