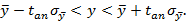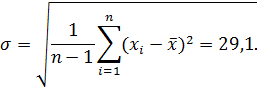Доверительная вероятность что это
Доверительная вероятность
3.3 доверительная вероятность: Вероятность того, что доверительный интервал накроет неизвестное истинное значение параметра, оцениваемого по выборочным данным.
* Вероятность того, что доверительный интервал накроет истинное значение оцениваемого параметра.
Величина, показывающая вероятность того, что действительное значение исследуемой переменной находится в принятом диапазоне значений
2.40. Доверительная вероятность
2.59. доверительная вероятность; уровень доверия
Полезное
Смотреть что такое «Доверительная вероятность» в других словарях:
доверительная вероятность — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN confidence coefficient … Справочник технического переводчика
ДОВЕРИТЕЛЬНАЯ ВЕРОЯТНОСТЬ — см. Доверительное оценивание … Математическая энциклопедия
доверительная вероятность, уровень доверия — 3.9 доверительная вероятность, уровень доверия (confidence coefficient, confidence level): Величина (1 a) вероятность, связанная с доверительным интервалом или со статистически накрывающим интервалом. Примечание Величину (1 a) часто выражают в… … Словарь-справочник терминов нормативно-технической документации
Односторонняя доверительная вероятность — вероятность того, что неизвестное истинное значение параметра не выйдет за пределы нижней (или верхней) границы доверительного интервала. Источник: ГОСТ 20522 96: Грунты. Методы статистической обработки результатов испытаний … Словарь-справочник терминов нормативно-технической документации
доверительная граница — 2.60. доверительная граница Каждая из границ, нижняя T1, верхняя T2 для двустороннего доверительного интервала или граница Т для одностороннего интервала Источник: ГОСТ Р 50779.10 2000: Статистические методы. Вероятность и основы статистики.… … Словарь-справочник терминов нормативно-технической документации
Доверительная зона — Теорема Колмогорова в математической статистике уточняет скорость сходимости выборочной функции распределения к её теоретическому аналогу. Содержание 1 Формулировка 1.1 Замечание 2 … Википедия
ГОСТ Р 50779.10-2000: Статистические методы. Вероятность и основы статистики. Термины и определения — Терминология ГОСТ Р 50779.10 2000: Статистические методы. Вероятность и основы статистики. Термины и определения оригинал документа: 2.3. (генеральная) совокупность Множество всех рассматриваемых единиц. Примечание Для случайной величины… … Словарь-справочник терминов нормативно-технической документации
ГОСТ 20522-96: Грунты. Методы статистической обработки результатов испытаний — Терминология ГОСТ 20522 96: Грунты. Методы статистической обработки результатов испытаний оригинал документа: Вероятность числовая характеристика степени возможности появления какого либо определенного события в тех или иных определенных условиях … Словарь-справочник терминов нормативно-технической документации
ГОСТ 20522-2012: Грунты. Методы статистической обработки результатов испытаний — Терминология ГОСТ 20522 2012: Грунты. Методы статистической обработки результатов испытаний оригинал документа: 3.1 вероятность: Числовая характеристика возможности появления какого либо определенного события в тех или иных определенных условиях … Словарь-справочник терминов нормативно-технической документации
Доверительная вероятность и доверительный интервал.
Вероятность того, что истинное значение измеряемой величины лежит внутри некоторого интервала, называется доверительной вероятностью, или коэффициентом надежности,а сам интервал — доверительным интервалом.
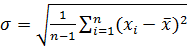
на так называемый коэффициент Стьюдента. Коэффициенты Стьюдента 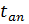
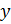
| Число измерений n | Доверительная вероятность y | ||
| 0,67 | 0,90 | 0,95 | 0,99 |
| 2,0 | 6,3 | 12,7 | 63,7 |
| 1,3 | 2,4 | 3,2 | 5,8 |
| 1,2 | 2,1 | 2,8 | 4,6 |
| 1,2 | 2,0 | 2,6 | 4,0 |
| 1,1 | 1,8 | 2,3 | 3,3 |
| 1,0 | 1,7 | 2,0 | 2,6 |
Окончательно, для измеряемой величины y при заданной доверительной вероятности y и числе измерений n получается условие
Величину 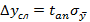
Пример: см. лекцию №5 – ряд чисел.
При числе измерений – 45 и доверительной вероятности – 0,95 получим, что коэффициент Стьюдента приблизительно равен 2,15. Тогда доверительный интервал для данного ряда измерений равен 62,6.
Источником грубых погрешностей нередко бывают резкие изменения условий измерения и ошибки, допущенные оператором:
— неправильный отсчет по шкале измерительного прибора, происходящий из-за неверного учета цены малых делений шкалы;
— неправильная запись результата наблюдений, значений отдельных мер использованного набора, например, гирь;
— хаотические изменения параметров напряжения, питающего средства измерения, например, его амплитуды или частоты.
Доверительный интервал — формула и примеры определения вероятности
В математической статистике при анализе и систематизации различных данных для подведения практических выводов часто используют метод доверительных интервалов. С его помощью выполняют определённую выборку среднего или доли с учётом стандартной ошибки. Благодаря этому достоверность вероятности увеличивается, так как оценка расширяется в обе стороны от исследуемой величины.
Общая схема построения
По сути, метод основан на модели классической математической статистики, подразумевающей бесконечно возможные выборки в генеральной совокупности. Пусть имеется главная выборка эпсилон с функцией распределения известной до некого параметра тау (Fe (x, τ)). Из этой генеральной совокупности получена выборка объёмом эн, включающая диапазон от x1 до xn. Этот параметр можно считать одномерным и принадлежащим диапазону от τ до R. Математически такое положение описывают как τ є T c R.
Если предположить, что для некоторого интервала йод, лежащего от нуля до единицы, существуют статистики S-(X|n|, J) и S+(X|n|, J), при этом им соответствует неравенство P< S-(X|n|, J) Свойство статистики и распределения
Таким образом, определить доверительную вероятность попадания тэта в интервал от S- до S+ можно от значения обратной функции в точках, равняющихся квантили статистики игрек порядка j/2 и 1 — j/2. При этом когда рассматриваемая функция монотонно убывает, знаки в неравенстве меняются на противоположные.
Пользуясь общим подходом расчёта доверительных интервалов, можно посчитать вероятность для нормальной генеральной совокупности, опираясь на ряд утверждений. Пусть известна выборка X|n,| взятая из совокупности E
N (j, ς 2 ), то есть имеющей нормальный закон распределения с математическим ожиданием j и дисперсией сигма в квадрате. Для такого состояния справедливо следующее:
Точный интервал
Существует ряд правил, позволяющих построить точные интервалы для математического ожидания и дисперсии нормально распределённой случайной величины. Есть два случая — при одном дисперсия может быть известной, а при другом нет. Следует обратить внимание, что точная доверительная вероятность строится с помощью общей схемы. Используют следующие правила для предоставления точных прогнозов:
Асимптотическое приближение
Однако не всегда можно рассчитать точный доверительный интервал. В этом случае строится приближённая вероятность — асимптотическая. Пусть для некоторого j Є (0,1) существует набор статистик S-(X|n|, j) и S-(X|n|, j), причём такие, что lim P< S-(X|n|, j) Примеры решения задач
Отсюда получают оценку: p = m / n. Теперь нужно убедиться, что p максимизирует функцию правдоподобия. То есть d2LnL / dp2 = — m / p2 — (n — m) / (1 — p)2 Использование онлайн-калькулятора
На практике довольно часто вычислить доверительную область не так уж и просто. Всё дело в том, что высокая вероятность часто находится в выборке большого объёма, поэтому приходится выполнять громоздкие вычисления. Учитывая, что доверительная вероятность определяет точность полученных результатов, другими словами, показывает, с какой вероятностью неправильное решение попадает в найденный интервал, обычно используют процент выборки от 95 до 99,9%.
Для высокой точности получения диапазона как раз и используют сервисы, которые в последнее время начали называться онлайн-калькуляторами. Это специализированные сайты, умеющие в автоматическом режиме решать различные математические задания. Особенность этих сайтов в том, что они предоставляют услуги бесплатно, при этом от их пользователей не требуется никаких знаний.
Всё что им нужно — это ввести в пролагаемую форму данные и нажать кнопку «Рассчитать». Система автоматически вычислит ответ и выведет его на экран. Из наиболее популярных можно отметить следующие сервисы:
Они доступны на русском языке, их интерфейс интуитивно понятен, поэтому воспользоваться их услугами сможет любой заинтересованный, имеющий доступ к интернету. Автоматический расчёт занимает буквально секунды, что составляет существенную разность по сравнению с затратой времени при самостоятельном вычислении.
Теория выборочного метода
| Главная > Учебные материалы > Математика: Теория выборочного метода | |||
 | |||
 | |||
| 1.Выборочный метод. 2.Оценка параметров выборочной совокупности. 3.Доверительная вероятность. Предельная ошибка выборки. | |||
1.Выборочный метод.
Одним из недостатков, который возникает при использовании выборочного метода, является ошибка репрезентативности. Данная ошибка возникает по причине того, что исследуется не вся совокупность, а выборочная.
Критерий, который должен соблюдаться при отборе объектов для изучения, является случайность. Иными словами, все объекты, отобранные для обследования, должны случайным образом попасть в выборочную совокупность. В противном случае результаты могут оказаться ложными.
Для отбора объектов, которые должны будут подвергнуты изучению, обычно используют один из двух способов образования выборки. Первый способ предусматривает возвращение объекта обследования в общую совокупность после его изучения. Второй способ предусматривает, что отобранный объект не будет возвращен в общую совокупность после его изучения.
Числовые характеристики выборочной совокупности называются соответственно выборочными. Основные характеристики:
Основной задачей выборочного метода наблюдений заключается в том, что бы оценить характеристики генеральной совокупности объектов исследования по данным выборочной совокупности.
2.Оценка параметров выборочной совокупности.
Пусть задана генеральная совокупность объектов исследования. Число объектов генеральной совокупности равно N. Число N имеет большое значение и исследовать всю совокупность не представляется возможным. По этой причине исследуют выборочную совокупность. И параметр 

Например, пусть параметр θ является математическим ожиданием случайной величины Х. Тогда оценкой 
Свойства оценок. Основными свойствами оценок является несмещенность, состоятельность и эффективность.
Несмещенность оценки означает ее отклонение от этого же параметра генеральной совокупности, т.е. математическое ожидание этой оценки равно оцениваемому параметру.
Если это равенство не выполняется, то полученная оценка является завышенной или заниженной.
Состоятельность означает приближение оценки к оцениваемому параметру при стремлении n к бесконечности. Или сходимость по вероятности к параметру генеральной совокупности.
Отсюда можно сделать вывод, что чем больше выборка n, тем точнее оцениваемый параметр.
Эффективной оценкой параметра θ называется такая несмещенная оценка 

3.Доверительная вероятность. Предельная ошибка выборки.
При исследовании выборочной совокупности рассчитанная средняя арифметическая может иметь некоторое отклонение от средней арифметической генеральной совокупности. Это отклонение называется ошибкой репрезентативности, которая возникает по причине исследования не всей, а выборочной совокупности. Наибольшее отклонение выборочной средней от средней арифметической генеральной совокупности, которое возможно при заданной доверительной вероятности называется предельной ошибкой выборки.
Построение доверительного интервала для генеральной средней по большой выборке.
Доверительный интервал для генеральной средней при n порядка нескольких сотен рассчитывается по следующей формуле:
переменная t равна:
Отсюда следует, что при заданной доверительной вероятности γ предельная ошибка выборочной средней равна произведению t (значение функции Лапласа) и средней квадратической ошибки.
Доверительный интервал генеральной средней рассчитывается по формуле:
Для нахождения предельной ошибки Δ необходимо найти среднюю квадратическую ошибку. Средняя квадратическая ошибка рассчитывается по следующей формуле:
При достаточно большом объеме выборки n выборочная дисперсия приближается к генеральной дисперсии, поэтому чем больше n, тем точнее значение средней квадратической ошибки.
Построение доверительного интервала для генеральной доли по большой выборке.
Если распределение выборочной доли w считать приблизительно нормальным, то для нахождения доверительного интервала для генеральной доли используем формулу предельную ошибки:
Из графика (рис.2) можно увидеть, что доверительный интервал находится внутри эллипса между значениями p1 и p2. И чем больше объем выборки n, тем эллипс становится более вытянутым и доверительный интервал становится более узким.
Можно вспомнить, что и дисперсия случайной величины, которая равна D(X) = npq для биномиального распределения, так же имеет максимальное значение в этой точке.
Пример.
В коммерческом банке из 5000 вкладов отобраны 792, которые распределены по группам в зависимости от их величины. Распределение вкладов имеет показательный закон распределения. Данные представлены в таблице.

Необходимо найти вероятность того, что средний размер вклада отличается от выборочной средней не более, чем 20 д.е. по абсолютной величине и найти так же границы, в которых с вероятностью 0.99 заключен средний размер вклада. Данные величины найти для повторной и бесповторной выборки. Найти вероятность того, что размер вклада будет заключен в пределах от 600 до 1000 д.е.
Решение.
Найдем выборочную среднюю арифметическую и выборочную дисперсию и построим гистограмму распределения частот.



Найдем границы, в которых с вероятностью 0.99 заключен средний размер вклада.

Найдем вероятность того, что размер вклада будет заключен в пределах от 600 до 1000 д.е.
Доверительный интервал и доверительная вероятность



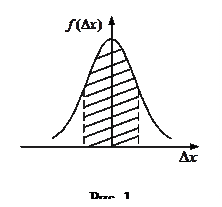
Для подавляющего большинства простых измерений достаточно хорошо выполняется так называемый нормальный закон случайных погрешностей (закон Гаусса), выведенный из следующих эмпирических положений.
1) погрешности измерений могут принимать непрерывный ряд значений;
2) при большом числе измерений погрешности одинаковой величины, но разного знака встречаются одинаково часто,
3) чем больше величина случайной погрешности, тем меньше вероятность ее появления.

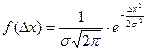
где 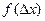


Величина σ не является случайной величиной и характеризует процесс измерений. Если условия измерений не изменяются, то σ остается постоянной величиной. Квадрат этой величины называют дисперсией измерений. Чем меньше дисперсия, тем меньше разброс отдельных значений и тем выше точность измерений.
Точное значение средней квадратичной ошибки σ, как и истинное значение измеряемой величины, неизвестно. Существует так называемая статистическая оценка этого параметра, в соответствии с которой средняя квадратичная ошибка равняется средней квадратичной ошибке среднего арифметического 
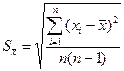
где 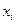
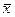
Чем больше число измерений, тем меньше 
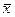

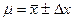
Интервал значений от 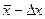
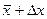

Все это справедливо для достаточно большого числа измерений, когда 
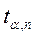


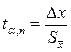
Функция распределения табулирована (табл.1). Значение коэффициента Стьюдента находится на пересечении строки, соответствующей числу измерений n, и столбца, соответствующего доверительной вероятности α
Таблица 1.
| n | α | n | α | ||||
| 0,8 | 0,9 | 0,95 | 0,98 | 0,8 | 0,9 | 0,95 | 0,98 |
| 1,9 | 2,9 | 4,3 | 7,0 | 1,5 | 2,0 | 2,6 | 3,4 |
| 1,6 | 2,4 | 3,2 | 4,5 | 1,4 | 1,9 | 2,4 | 3,1 |
| 1,5 | 2,1 | 2,8 | 3,7 | 1,4 | 1,9 | 2,4 | 3,9 |
Пользуясь данными таблицы, можно:
1) определить доверительный интервал, задаваясь определенной вероятностью;
2) выбрать доверительный интервал и определить доверительную вероятность.
При косвенных измерениях среднюю квадратичную ошибку среднего арифметического значения функции 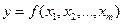
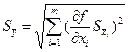
Доверительный интервал и доверительная вероятность определяются так же, как и в случае прямых измерений.