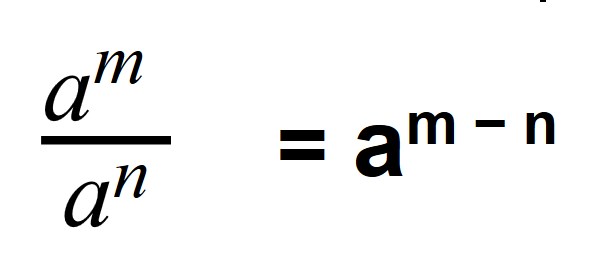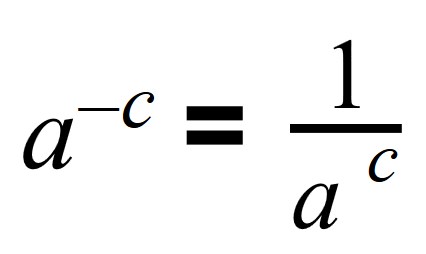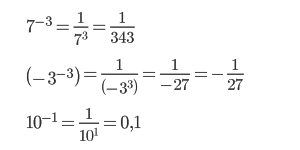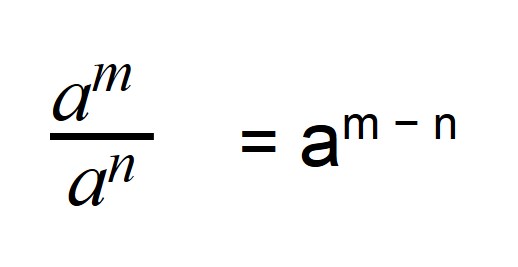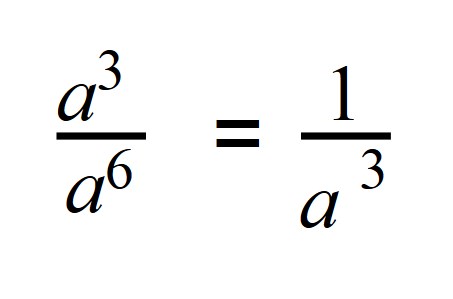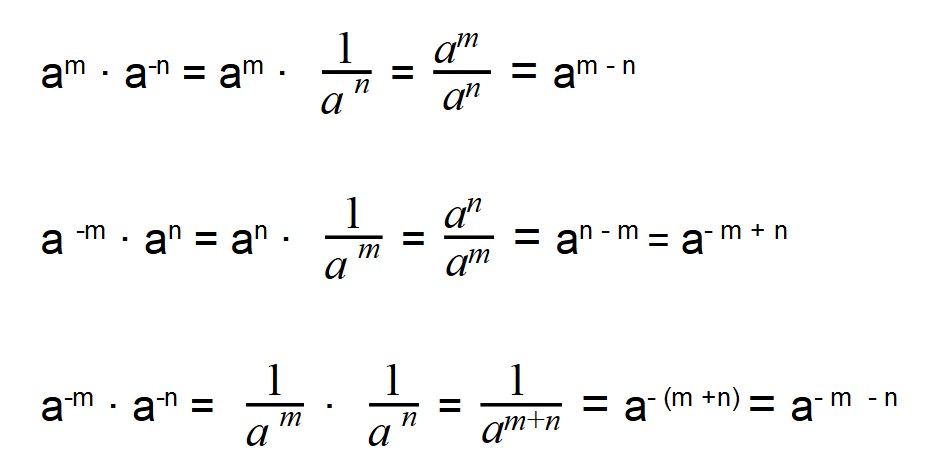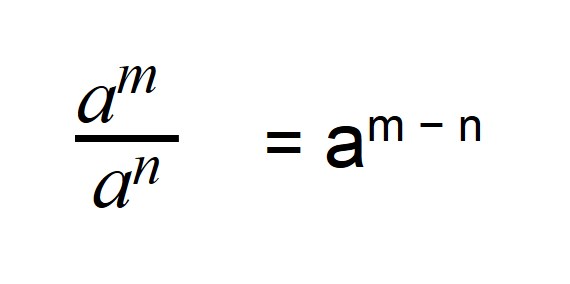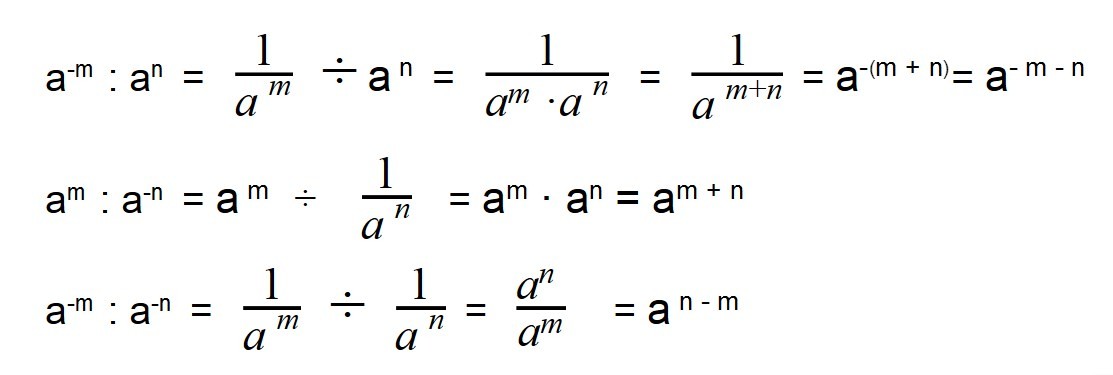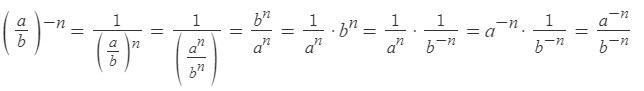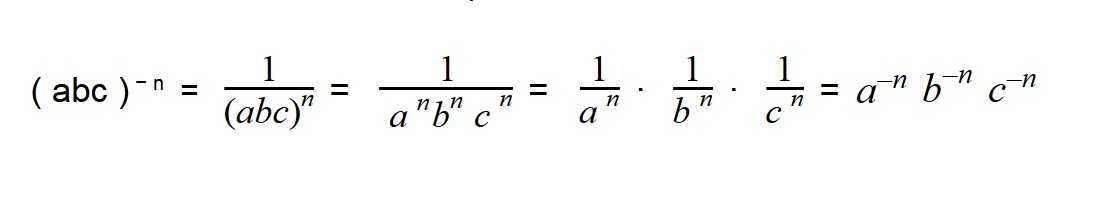Дробная степень это что значит
Дробная степень
Какими свойствами обладает степень с дробным показателем (дробная степень)? Как выполнить возведение числа в дробную степень?
1) Степенью числа a (a>0) с рациональным показателем r
где m — целое число, n — натуральное число (n>1), называется число
При a
Выполнить возведение в дробную степень:
Если показатель степени — десятичная дробь, нужно предварительно перевести ее в обыкновенную.
Смешанное число нужно предварительно перевести в неправильную дробь:
А как вычисляется отрицательная дробная степень?
Степень с отрицательным рациональным показателем также определена только для a>0:
При возведении обыкновенной дроби в степень с отрицательным показателем удобно использовать формулу:
Выполнить возведение в степень с отрицательным рациональным показателем:
Дробная степень числа
Дробный показатель
Число с дробным показателем степени равно корню с показателем, равным знаменателю, и подкоренным числом в степени, равной числителю.
Чтобы разобраться, почему число в дробной степени равно корню, надо вспомнить правило извлечения корня из степени:
Чтобы извлечь корень из степени, надо показатель степени разделить на показатель корня:
Следовательно, если показатель степени не делится на показатель корня, то получается дробная степень:
Поэтому извлечение корня всегда может быть заменено возведением в степень.
Действия над степенями с дробными показателями
Действия над степенями с дробными показателями совершаются по тем же правилам, которые установлены для степеней с целым показателем.
При доказательстве этого положения, будем сначала предполагать, что члены дробей: 

В частном случае n или q могут равняться единице.
При умножении дробных степеней с одинаковыми основаниями их показатели складываются:
При делении дробных степеней с одинаковыми основаниями из показателя делимого вычитается показатель делителя:
Чтобы возвести степень в другую степень, в случае дробных показателей, достаточно перемножить показатели степеней:
Чтобы извлечь корень из дробной степени, достаточно показатель степени разделить на показатель корня:
Правила действий применимы не только к положительным дробным показателям, но и к отрицательным.
Возведение в степень: правила, примеры
Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.
Понятие возведения в степень
Начнем с формулирования базовых определений.
Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.
Как возвести число в натуральную степень
Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.
Решение
Возьмем пример посложнее.
Вычислите значение 3 2 7 2
Решение
Выполним эти действия и получим ответ: 3 2 7 · 3 2 7 = 23 7 · 23 7 = 529 49 = 10 39 49
Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.
Решение
Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:
Это понятно из записи 
От основания степени это не зависит.
Как возвести число в целую степень
В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.
Решение
Решение
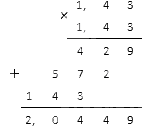
Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:
Как возвести число в дробную степень
Проиллюстрируем на примере.
Решение
Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.
Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.
Решение
Как возвести число в иррациональную степень
Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.
Вычислите приближенное значение 2 в степени 1,174367.
Решение
Свойства степеней и действия с ними
Зачем нужны степени? Где они тебе пригодятся? Почему тебе нужно тратить время на их изучение?
Как обычно — чтобы облегчить себе жизнь. Знание свойств степеней позволит тебе упрощать вычисления и считать быстрее, что пригодится и в жизни и на ОГЭ или ЕГЭ!
Чтобы узнать все о степенях и научиться пользоваться свойствами степеней, читай эту статью.
P.S Если ты хорошо знаешь степени и тебе надо только повторить, переходи сразу к продвинутому уровню.
НАЧАЛЬНЫЙ УРОВЕНЬ
Степени. Коротко о главном
Определение степени:
Свойства степеней:
| Произведение степеней с одинаковым основанием: | \( <^ |
| Произведение степеней с одинаковыми показателями: | \( <^ |
| Деление степеней с одинаковым основанием: | \( \frac<<^ |
| Деление степеней с одинаковыми показателями: | \( \frac<<^ |
| Возведение степени в степень: | \( <<\left( <^ |
| Дробная степень: | \( <^<\frac |
Особенности степеней:
Возведение в степень – это такая же математическая операция, как сложение, вычитание, умножение или деление.
Сейчас объясню все человеческим языком на очень простых примерах. Будь внимателен. Примеры элементарные, но объясняющий важные вещи. Начнем со сложения.
Сложение
Объяснять тут нечего. Ты и так все знаешь: нас восемь человек. У каждого по две бутылки колы. Сколько всего колы? Правильно – 16 бутылок. Теперь умножение.
Умножение
Тот же самый пример с колой можно записать по-другому: \(\displaystyle 2\cdot 8=16\).
Математики — люди хитрые и ленивые. Они сначала замечают какие-то закономерности, а потом придумывают способ как быстрее их «считать».
В нашем случае они заметили, что у каждого из восьми человек одинаковое количество бутылок колы и придумали прием, который называется умножением.
Согласись, \(\displaystyle 2\cdot 8=16\) считается легче и быстрее, чем \(\displaystyle 2+2+2+2+2+2+2+2=16\).
И еще одна важная деталь. Ошибок при таком счете делается гораздо меньше. Математики из Стэнфорда, кстати, считают, что человек, знающий приемы счета, делает это в два раза легче и быстрее и совершает в два раза меньше ошибок. Работы меньше, а результат лучше.
Итак, чтобы считать быстрее, легче и без ошибок, нужно всего лишь запомнить таблицу умножения. Ты, конечно, можешь делать все медленнее, труднее и с ошибками, но лучше ее запомнить! Вот таблица умножения. Выучи ее наизусть.
И другая таблица, красивее:
А какие еще хитрые приемы счета придумали ленивые математики? Правильно – возведение числа в степень.
Возведение числа в степень
Если тебе нужно умножить число само на себя пять раз, то математики говорят, что тебе нужно возвести это число в пятую степень.
Например, \(\displaystyle 2\cdot 2\cdot 2\cdot 2\cdot 2=<<2>^<5>>\). Математики помнят, что два в пятой степени – это \(\displaystyle 32\).
И решают такие задачки в уме – быстрее, легче и без ошибок.
Для этого нужно всего лишь запомнить то, что выделено цветом в таблице степеней чисел. Поверь, это сильно облегчит тебе жизнь.
Кстати, почему вторую степень называют квадратом числа, а третью — кубом? Что это значит? Очень хороший вопрос. Сейчас будут тебе и квадраты, и кубы.
Примеры из жизни
Начнем с квадрата или со второй степени числа.
Представь себе квадратный бассейн размером \( \displaystyle 3\) метра на \( \displaystyle 3\) метра. Бассейн стоит у тебя на даче. Жара и очень хочется купаться.
Но… бассейн без дна! Нужно застелить дно бассейна плиткой. Сколько тебе надо плитки? Для того чтобы это определить, тебе нужно узнать площадь дна бассейна.
Ты можешь просто посчитать, тыкая пальцем, что дно бассейна состоит из \( \displaystyle 9\) кубиков метр на метр. Если у тебя плитка метр на метр, тебе нужно будет \( \displaystyle 9\) кусков. Это легко…
Но где ты видел такую плитку? Плитка скорее будет \( \displaystyle 10\) см на \( \displaystyle 10\) см. И тогда «пальцем считать» замучаешься. Тогда придется умножать.
Итак, по одной стороне дна бассейна у нас поместится \( \displaystyle 30\) плиток (\( \displaystyle \frac<300\ см><10\ см>=30\) штук) и по другой тоже \( \displaystyle 30\) плиток.
Ты заметил, что для определения площади дна бассейна мы умножили одно и то же число само на себя? Что это значит? Раз умножается одно и то же число, мы можем воспользоваться приемом «возведение в степень».
Конечно, когда у тебя всего два числа, все равно перемножить их или возвести в степень. Но если у тебя их много, то возводить в степень значительно проще и ошибок при расчетах получается тоже меньше.
Иными словами, вторую степень числа всегда можно представить в виде квадрата. И наоборот, если ты видишь квадрат – это ВСЕГДА вторая степень какого-то числа.
Квадрат – это изображение второй степени числа.
Теперь куб или третья степень числа. Тот же самый бассейн. Но теперь тебе нужно узнать, сколько воды придется залить в этот бассейн. Тебе нужно посчитать объем. (Объемы и жидкости, кстати, измеряются в кубических метрах. Неожиданно, правда?)
Нарисуй бассейн: дно размером \( \displaystyle 3\) на \( \displaystyle 3\) метра и глубиной \( \displaystyle 3\) метра и попробуй посчитать, сколько всего кубов размером метр на метр войдет в твой бассейн.
Прямо показывай пальцем и считай! Раз, два, три, четыре…двадцать два, двадцать три… Сколько получилось? Не сбился? Трудно пальцем считать?
Так-то! Бери пример с математиков. Они ленивы, поэтому заметили, что чтобы посчитать объем бассейна, надо перемножить друг на друга его длину, ширину и высоту.
В нашем случае объем бассейна будет равен \( \displaystyle 3\cdot 3\cdot 3=27\) кубов… Легче правда?
А теперь представь, насколько математики ленивы и хитры, если они и это упростили. Свели все к одному действию. Они заметили, что длина, ширина и высота равна и что одно и то же число перемножается само на себя…
Остается только запомнить таблицу степеней. Если ты, конечно, такой же ленивый и хитрый как математики. Если любишь много работать и делать ошибки – можешь продолжать считать пальцем.
Ну и чтобы окончательно убедить тебя, что степени придумали лодыри и хитрюги для решения своих жизненных проблем, а не для того чтобы создать тебе проблемы, вот тебе еще пара примеров из жизни.
У тебя есть \( \displaystyle 2\) миллиона рублей. В начале каждого года ты зарабатываешь на каждом миллионе еще один миллион. То есть каждый твой миллион в начале каждого года удваивается. Сколько денег у тебя будет через \( \displaystyle 5\) лет?
Если ты сейчас сидишь и «считаешь пальцем», значит ты очень трудолюбивый человек и.. глупый. Но скорее всего ты дашь ответ через пару секунд, потому что ты – умный! Итак, в первый год — два умножить на два… во второй год — то, что получилось, еще на два, в третий год… Стоп!
Ты заметил, что число \( \displaystyle 2\) перемножается само на себя \( \displaystyle 6\) раз. Значит, два в шестой степени – \( \displaystyle 64\) миллиона! А теперь представь, что у вас соревнование и эти \( \displaystyle 64\) миллиона получит тот, кто быстрее посчитает…
Стоит запомнить степени чисел, как считаешь?
У тебя есть \( \displaystyle 1\) миллион. В начале каждого года ты зарабатываешь на каждом миллионе еще два. Здорово правда? Каждый миллион утраивается. Сколько денег у тебя будет через \( \displaystyle 4\) года?
Уже скучно, потому что ты уже все понял: три умножается само на себя \( \displaystyle 4\) раза.
Теперь ты знаешь, что с помощью возведения числа в степень ты здорово облегчишь себе жизнь. Давай дальше посмотрим на то, что можно делать со степенями и что тебе нужно знать о них.
Отрицательная степень
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Что такое степень числа
В учебниках по математике можно встретить такое определение:
«Степенью n числа а является произведение множителей величиной а n раз подряд»
Например, a n — степень, где:
Читается такое выражение как a в степени n.
Если говорить проще, то степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить данное число (основание степени) само на себя.
А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:
Таблица степеней
Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).
Свойства степеней
Степень с натуральным показателем в математике имеет несколько важных свойств, которые позволяют упрощать вычисления. Всего их пять штук — ниже мы их рассмотрим.
Свойство 1: произведение степеней
При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели степеней складываем:
Свойство 2: частное степеней
Когда мы делим степени с одинаковыми основаниями, то основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя.
Свойство 3: возведение степени в квадрат
Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.
Свойство 4: степень произведения
При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.
Свойство 5: степень частного
Чтобы возвести в степень частное, можно возвести в эту степень сначала делимое, потом делитель, и первый результат разделить на второй.
Степень с показателем 0
Любое целое a ≠ 0 в степени 0 равно 1.
Выражение 0 в степени 0 многие математики считают лишенным смысла, так график функции f (x, у) = xy прерывается в точке (0; 0).
Степень с отрицательным показателем
Число в минусовой степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем:
Чтобы разобраться, как возводить число в отрицательную степень, вспомним правило деления степеней с одинаковыми основаниями.
Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
Поэтому если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:
Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:
Действия с отрицательными степенями
Умножение отрицательных степеней
При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются, так же как и при умножении положительных степеней:
Деление отрицательных степеней
При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя, так же как и при делении положительных степеней:
Возведение дроби в отрицательную степень
Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:
Возведение произведения в отрицательную степень
Чтобы возвести произведение в отрицательную степень, необходимо возвести в эту степень каждый множитель произведения отдельно: