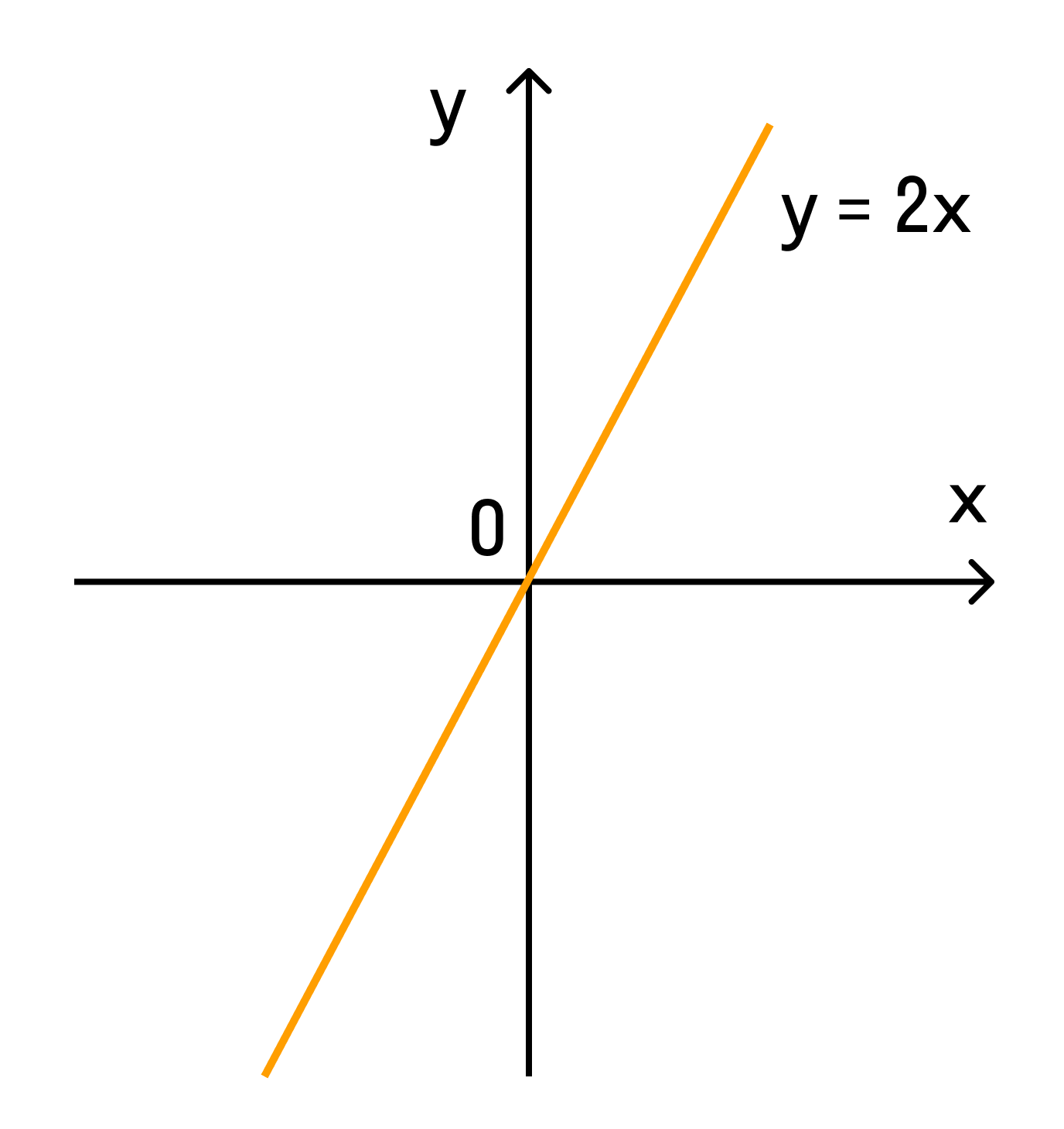Другие величины что это

Словари

1. Одно из основных математических понятий, отражающее идею измерения меняющихся объектов.

2. Протяженность, объём, размер чего-либо.

3. Количество чего-либо, имеющего ценность в денежном выражении.

4. Сила или степень проявления какого-либо явления, свойства и т.п.

Человек, являющийся выдающимся в какой-либо сфере деятельности.

Морфология: (нет) чего? величины́, чему? величине́, (вижу) что? величину́, чем? величино́й, о чём? о величине́; мн. что? величи́ны, (нет) чего? величи́н, чему? величи́нам, (вижу) что? величи́ны, чем? величи́нами, о чём? о величи́нах

1. Величиной какой-либо денежной суммы называется количество денежных единиц, составляющих её.

Величина прожиточного минимума, социального пособия. | Средняя величина учительской зарплаты. | Величина уставного капитала.

2. Величиной какого-либо объекта называется его размер по показателям объёма, занимаемой площади, длины и т. п.

Величина здания. | Величина ёмкости аккумулятора.

3. Говоря о предмете определённой величины, вы даёте характеристику его размерам.

Море огромной величины. | Медведь гигантской величины. | Гвоздь средней величины.

4. Когда вы говорите, что какой-то предмет величиной с или величиной в какой-либо предмет, вы хотите сказать, что первый предмет одинаков по размеру с другим предметом, который более знаком вашему собеседнику или более стабилен по своему размеру.

Они нашли какой-то круглый предмет величиной с теннисный мяч. | Он мог спокойно съесть бутерброд величиной в кирпич.

5. Когда какой-то памятник, портрет, макет и т. п. сделан в натуральную величину, это означает, что он соответствует размерам реальных объектов.

Памятник Чижику-Пыжику в Петербурге выполнен в натуральную птичью величину. | А вы можете вылепить слона в натуральную величину?

6. Если вы говорите о ком-либо, что он звезда первой величины, вы хотите сказать, что он находится на самом высоком уровне профессионализма, общественного признания, интереса.

7. В математике величиной называют любой числовой показатель, с которым можно производить расчёты.

Постоянная, переменная, статичная величина.

8. Неизвестной величиной называют математическую переменную, значение которой заранее неизвестно и его необходимо вычислить. Это же выражение используют, когда говорят о каких-то неясных жизненных ситуациях или загадочных людях.

9. Когда какого-либо человека называют величиной в какой-либо области деятельности, имеют в виду, что он достиг в ней больших успехов.

ВЕЛИЧИНА́, величины, мн. величины, величинам (книжн.), и (разг.) величины, величинам, жен.

1. только ед. Размер, объем, протяжение вещи. Величина стола достаточная. Комната громадной величины.

2. Всё, что можно измерить и исчислить (мат. физ.). Бесконечно малая величина. Неизвестная величина. Переменная величина. Учение о величинах.

|| перен. Всё, имеющее общественную ценность, значение (книжн.). Литературная величина (о значительном писателе).

1. Размер, объём, протяжённость предмета. Площадь большой величины. Измерить величину чего-н.

2. То, что можно измерить, исчислить. Равные величины.

3. О человеке, выдающемся в какой-н. области деятельности. Этот учёный мировая в.

1) Обобщение конкретных понятий: длины, площади, веса, давления и т. п. (чего-л. измеряемого, сопоставляемого).

Величиной с ладонь.

Бесконечно большая величина.

Несмотря на величину оранжереи, им [растениям] было в ней тесно (Гаршин).

габари́ты, ме́ра, разме́р

2) перен., только ед. О человеке выдающемся в какой-л. области деятельности.

Стал величиной в хирургии.

звезда́, знамени́тость, изве́стность (разг.), и́мя, корифе́й (высок.), свети́ло

Производное от великий.

О человеке, выделяющемся среди других, выдающемся в какой-л. области деятельности.

Размер (объем, протяженность, площадь) предмета, который как-л. измеряется;

Син.: размер и размеры, габарит.

Небольшой по величине сосуд был наполнен мутноватой жидкостью.

1. только ед. Размер (объём, площадь, протяжённость и т.п.) какого-л. объекта, предмета, имеющего видимые физические границы. В. здания. В. стадиона. Величиной с булавку. Величиной в ладонь. Отверстие бо́льшей величины. В натуральную величину (в соответствии с действительными, естественными размерами). // Количество чего-л., имеющего ценность в денежном выражении. В. авторского гонорара. В. штрафа.

2. Количественное выражение физического признака какого-л. явления. Измерить величину тока. Определить максимальные величины скорости движения. // Матем. Всё то, что можно измерить и исчислить. Вещественная в. (любое целое положительное число). Логическая в. (принимающая значение «да», «нет»). Постоянная, переменная в. Равные величины. Свойства величин. Символьная в. (т.е. имеющая значение данного символа, например: +, > и т.п.).

величина́ (матем.), 1) Обобщение конкретных понятий: длины, площади, веса и т. п. Выбрав одну из величин данного рода за единицу измерения, можно выразить числом отношение любой другой величины того же рода к единице измерения. 2) В более общем смысле скалярной величиной, или скаляром, называется объект, полностью характеризующийся заданием одного числа. Обобщением скалярных величин являются векторные величины (см. Вектор), тензорные величины (см. Тензорное исчисление).

1) обобщение конкретных понятий: длины, площади, веса и т. п. Выбрав одну из величин данного рода за единицу измерения, можно выразить числом отношение любой другой величины того же рода к единице измерения.

2) В более общем смысле скалярной величиной, или скаляром, называется объект, полностью характеризующийся заданием одного числа. Обобщением скалярных величин являются векторные величины (см. Вектор (см. ВЕКТОР (в математике))), тензорные величины (см. Тензорное исчисление (см. ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ)).

2) В более общем смысле скалярной величиной, или скаляром, называется объект, полностью характеризующийся заданием одного числа. Обобщением скалярных величин являются векторные величины (см. Вектор), тензорные величины (см. Тензорное исчисление).

1. Размер, объем, протяженность чего-л.

Это пароход морского типа средней величины. Чехов, Остров Сахалин.

Иволги, красивые оранжево-желтые птицы, величиной с голубя, сидели на высоких деревьях. Арсеньев, По Уссурийской тайге.

Конструкция была вычерчена до мельчайших деталей в натуральную величину. Бек, Талант.

Все то, что можно измерить и исчислить.

Постоянная величина. Переменная величина.

3. О человеке, выдающемся в какой-л. области деятельности.

Гельмгольц, крупнейшая величина в естествознании, был в философии непоследователен, как и громадное большинство естествоиспытателей. Ленин, Материализм и эмпириокритицизм.

— звезда первой величины

ВЕЛИЧИНА, обобщение конкретных понятий: длины, площади, веса и т.д. Выбор одной из величин данного рода (единицы измерения) позволяет сравнивать (соизмерять) величины. Развитие понятия величина привело к скалярным величинам, характеризующимся числом (смотри Скаляр), векторным величинам, характеризующимся числом и направлением (смотри Вектор), и к другим величинам.

величиной в и величиной с.

1. величиной в (при выражении в единицах измерения). Участок величиной в два гектара.

2. величиной с (при указании на предмет, к которому приравнивается по размерам другой предмет). Иволги, красивые оранжево-желтые, птицы, величиной с голубя (Арсеньев).

величина́, величи́ны, величины́, величи́н, величине́, величи́нам, величину́, величино́й, величино́ю, величи́нами, величи́нах

Источник

Прямая и обратная пропорциональность

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные определения

Математическая зависимость — это соответствие между элементами двух множеств, при котором каждому элементу одного множества ставится в соответствие элемент из другого множества.

Зависимости также можно классифицировать по формам: функциональная и статистическая.

Функциональная зависимость между двумя переменными величинами характеризуется тем, что каждому значению одной из них соответствует вполне определенное и единственное значение другой.

В математике функциональной зависимостью переменной Y от переменной Х называют зависимость вида y = f(x), где каждому допустимому значению X ставится в соответствие по определенному правилу единственно возможное значение Y.

Статистическая зависимость — это зависимость случайных величин, когда изменение одной переменной приводит к изменению другой.

Если изменение одной из случайных величин влечет изменение среднего другой случайной величины, то статистическую зависимость называют корреляционной. Сами случайные величины, связанные корреляционной зависимостью, оказываются коррелированными.

Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.

Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз. Проще говоря — это зависимость одного числа от другого.

Есть две разновидности пропорциональностей:

Коэффициент пропорциональности — это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.

Прямо пропорциональные величины

Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.

Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».

Свойство прямо пропорциональной зависимости:

Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.

Примеры прямо пропорциональной зависимости:

Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.

Формула прямой пропорциональности

y = kx,

где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности.

Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.

Формула коэффициента прямой пропорциональности:

Графиком прямо пропорциональной зависимости величин является прямая линия.

Например, при k = 2 график выглядит так:

Пример 1.

В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.

Пример 2.

Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней?

Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.

Если разделить 420 на 14, узнаем, что объем увеличивается в 30 раз.

Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз. Таким образом:

Ответ: 20 человек напишут 420 постов за 12 дней.

Обратно пропорциональные величины

Две величины называют обратно пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая уменьшается (или увеличивается) во столько же раз.

Объясним, что значит обратно пропорционально в виде схемы: «больше — меньше» или «меньше — больше».

Свойство обратной пропорциональности величин:

Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.

Примеры обратно пропорциональной зависимости:

Формула обратной пропорциональности

где y и x — это переменные величины,

k — постоянная величина, которую называют коэффициентом обратной пропорциональности.

Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.

Формула коэффициента обратной пропорциональности:

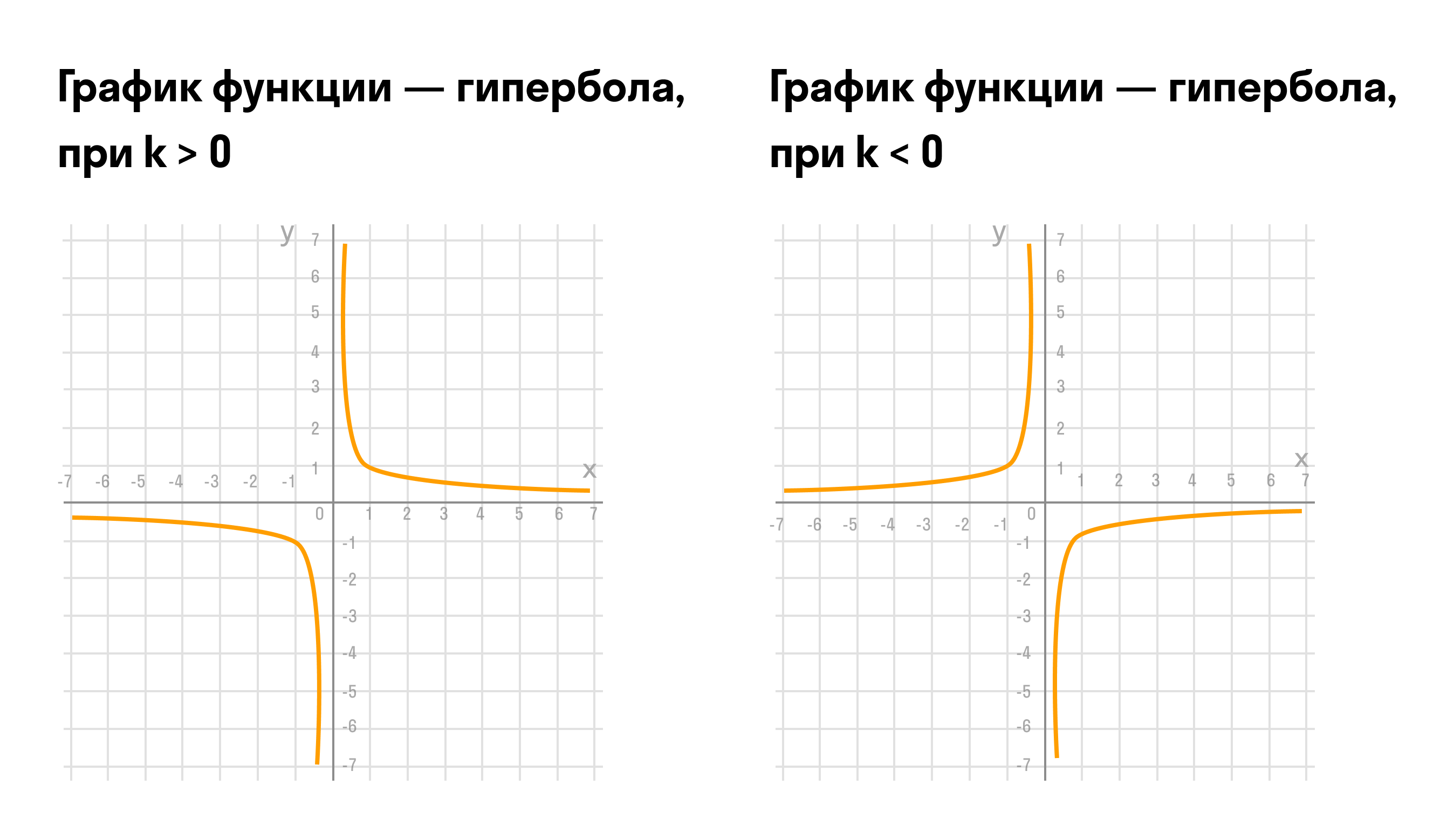
Графиком обратно пропорциональной зависимости величин является гипербола.

Свойства функции обратной пропорциональности:

Потренируемся

Пример 1. 24 человека за 5 дней раскрутили канальчик в ютубе. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?

Пример 2. Автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?

Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.

Соотношения равны, но перевернуты относительно друг друга.

Источник

Величина

Величина — одно из основных математических понятий, смысл которого с развитием математики подвергался ряду обобщений.

Содержание

История

Ещё в «Началах» Евклида (3 в. до н. э.) были отчётливо сформулированы свойства величины, называемых теперь, для отличия от дальнейших обобщений, положительными скалярными величинами. Это первоначальное понятие величины является непосредственным обобщением более конкретных понятий: длины, площади, объёма, массы и т. п. Каждый конкретный род величины связан с определённым способом сравнения физических тел или др. объектов. Например, в геометрии отрезки сравниваются при помощи наложения, и это сравнение приводит к понятию длины: два отрезка имеют одну и ту же длину, если при наложении они совпадают; если же один отрезок накладывается на часть другого, не покрывая его целиком, то длина первого меньше длины второго. Общеизвестны более сложные приёмы, необходимые для сравнения плоских фигур по площади или пространственных тел по объёму.

Свойства

В более общем смысле слова величинами называют векторы, тензоры и другие «не скалярные величины». Такие величины можно складывать, но отношение неравенства (а 0).

Так как система действительных положительных чисел удовлетворяет перечисленным выше свойствам 1-10, а система всех действительных чисел обладает всеми свойствами скалярных величин, то вполне законно сами действительные числа называть величинами. Это особенно принято при рассмотрении переменных величин. Если какая-либо конкретная величина, например длина l нагреваемого металлического стержня, изменяется во времени, то меняется и измеряющее её число х = l / l_o (при постоянной единице измерения l_o). Само это меняющееся во времени число х принято называть переменной величиной и говорить, что х принимает в какие-либо последовательные моменты времени t₁, t₂,… «числовые значения» X₁, X₂,… В традиционной математической терминологии говорить о «переменных числах» не принято. Однако логичнее такая точка зрения: числа, как и длины, объёмы и т. п., являются частными случаями величины и, как всякие величины, могут быть и переменными, и постоянными. Столь же законно и рассмотрение переменных векторов, тензоров и т. п.

Источник

Физическая величина

Физи́ческая величина́ — физическое свойство материального объекта, физического явления, процесса, которое может быть охарактеризовано количественно.

Значение физической величины — одно или несколько (в случае тензорной физической величины) чисел, характеризующих эту физическую величину, с указанием единицы измерения, на основе которой они были получены.

Размер физической величины — значения чисел, фигурирующих в значении физической величины.

Например, автомобиль может быть охарактеризован с помощью такой физической величины, как масса. При этом, значением этой физической величины будет, например, 1 тонна, а размером — число 1, или же значением будет 1000 килограмм, а размером — число 1000. Этот же автомобиль может быть охарактеризован с помощью другой физической величины — скорости. При этом, значением этой физической величины будет, например, вектор определённого направления 100 км/ч, а размером — число 100.

Размерность физической величины — единица измерения, фигурирующая в значении физической величины. Как правило, у физической величины много различных размерностей: например, у длины — нанометр, миллиметр, сантиметр, метр, километр, миля, дюйм, парсек, световой год и т. д. Часть таких единиц измерения (без учёта своих десятичных множителей) могут входить в различные системы физических единиц — СИ, СГС и др.

Часто физическая величина может быть выражена через другие, более основополагающие физические величины. (Например, сила может быть выражена через массу тела и его ускорение). А значит, соответственно, и размерность такой физической величины может быть выражена через размерности этих более общих величин. (Размерность силы может быть выражена через размерности массы и ускорения). (Часто такое представление размерности некоторой физической величины через размерности других физических величин является самостоятельной задачей, которая в некоторых случаях имеет свой смысл и назначение.) Размерности таких более общих величин часто уже являются основными единицами той или другой системы физических единиц, то есть такими, которые сами уже не выражаются через другие, ещё более общие величины.

Пример.
Если физическая величина мощность записывается как

P = 42,3 × 10³ Вт = 42,3 кВт,

Р — это общепринятое литерное обозначение этой физической величины, 42,3 × 10³ Вт — значение этой физической величины, 42,3 × 10³ — размер этой физической величины.

Вт — это сокращённое обозначение одной из единиц измерения этой физической величины (ватт). Литера к является обозначением десятичного множителя «кило» Международной системы единиц (СИ).

Содержание

Размерные и безразмерные физические величины

Аддитивные и неаддитивные физические величины

Экстенсивные и интенсивные физические величины

Некоторые физические величины, такие как момент импульса, площадь, сила, длина, время, не относятся ни к экстенсивным, ни к интенсивным.

От некоторых экстенсивных величин образуются производные величины:

Скалярные, векторные, тензорные величины

Система единиц физических величин

Система единиц физических величин — совокупность единиц измерений физических величин, в которой существует некоторое число так называемых основных единиц измерений, а остальные единицы измерения могут быть выражены через эти основные единицы. Примеры систем физических единиц — Международная система единиц (СИ), СГС.

Символы физических величин

В качестве символов физических величин обычно выступают отдельные прописные и строчные литеры латинского или греческого алфавита. Часто к обозначениям добавляют верхние или нижние индексы, обозначающие, к чему относится величина, например E_п часто обозначает потенциальную энергию, а c_p — теплоёмкость при постоянном давлении.

Источник

величина

Полезное

Смотреть что такое «величина» в других словарях:

величина — сущ., ж., употр. сравн. часто Морфология: (нет) чего? величины, чему? величине, (вижу) что? величину, чем? величиной, о чём? о величине; мн. что? величины, (нет) чего? величин, чему? величинам, (вижу) что? величины, чем? величинами, о чём? о… … Толковый словарь Дмитриева

ВЕЛИЧИНА — ВЕЛИЧИНА, величины, мн. величины, величинам (книжн.), и (разг.) величины, величинам, жен. 1. только ед. Размер, объем, протяжение вещи. Величина стола достаточная. Комната громадной величины. 2. Всё, что можно измерить и исчислить (мат. физ.).… … Толковый словарь Ушакова

величина — Размер, формат, калибр, доза, рост, объем, протяжение. Ср … Словарь синонимов

величина — ВЕЛИЧИНА1, ы, ж Разг. О человеке, выделяющемся среди других, выдающемся в какой л. области деятельности. Н. Коляда крупная величина в современной драматургии. ВЕЛИЧИНА2, ы, мн величины, ж Размер (объем, протяженность, площадь) предмета, который… … Толковый словарь русских существительных

ВЕЛИЧИНА — ВЕЛИЧИНА, обобщение конкретных понятий: длины, площади, веса и т.д. Выбор одной из величин данного рода (единицы измерения) позволяет сравнивать (соизмерять) величины. Развитие понятия величина привело к скалярным величинам, характеризующимся… … Современная энциклопедия

ВЕЛИЧИНА — ВЕЛИЧИНА, ы, мн. ины, ин, жен. 1. Размер, объём, протяжённость предмета. Площадь большой величины. Измерить величину чего н. 2. То, что можно измерить, исчислить. Равные величины. 3. О человеке, выдающемся в какой н. области деятельности. Этот… … Толковый словарь Ожегова

величина — ВЕЛИЧИНА, размер, размеры … Словарь-тезаурус синонимов русской речи

Величина — ВЕЛИЧИНА, обобщение конкретных понятий: длины, площади, веса и т.д. Выбор одной из величин данного рода (единицы измерения) позволяет сравнивать (соизмерять) величины. Развитие понятия величина привело к скалярным величинам, характеризующимся… … Иллюстрированный энциклопедический словарь

ВЕЛИЧИНА — в математике 1) обобщение конкретных понятий: длины, площади, веса и т. п. Выбрав одну из величин данного рода за единицу измерения, можно выразить числом отношение любой другой величины того же рода к единице измерения.2) В более общем смысле… … Большой Энциклопедический словарь

величина́ — величина, ы; мн. величины, ин … Русское словесное ударение

Источник