Dsp system toolbox matlab что это
Документация
С DSP System Toolbox можно проектировать и анализировать КИХ, БИХ, многоскоростные, многоступенчатые, и адаптивные фильтры. Можно передать сигналы потоком от переменных, файлов данных и сетевых устройств для разработки системы и верификации. Time Scope, Спектр Анализатор и Logic Analyzer позволяют вам динамически визуализировать и измерить сигналы потоковой передачи. Для анализа прототипа и развертывания на встраиваемых процессорах, включая ARM ® Кора ® архитектуры, тулбокс поддерживает генерацию кода C/C++. Это также поддерживает побитовое моделирование фиксированной точки и генерацию HDL-кода от фильтров, БПФ, ОБПФ и других алгоритмов.
Алгоритмы доступны как функции MATLAB, Системные объекты и блоки Simulink.
Запуск
Изучите основы DSP System Toolbox
Генерация сигнала, манипуляция и анализ
Создание, импорт, экспорт, отображение и управление сигналов
Создание фильтра и анализ
КИХ, БИХ, частотные преобразования
Внедрение фильтра
Односкоростные, многоскоростные, и адаптивные фильтры
Преобразования и спектральный анализ
БПФ, DCT, спектральный анализ, линейное предсказание
Статистика и линейная алгебра
Измерения, статистика, матричная математика, линейная алгебра
Проект фиксированной точки
Преобразование из плавающей запятой в фиксированную запятую, проектирование алгоритма с фиксированной запятой
Генерация кода
Ускорение симуляции, генерация кода, оптимизация для процессоров ARM Cortex-M и процессоров ARM Cortex-A
Приложения
Симулируйте радар, коммуникацию и биомедицинские системы
DSP System Toolbox Поддерживаемые аппаратные средства
Поддержка стороннего оборудования, такого как ARM Cortex-M и процессоры ARM Cortex-A
Документация
Алгоритмы доступны как функции MATLAB, Системные объекты и блоки Simulink.
Примеры
Потоковая обработка сигналов
Этот пример показывает, как использовать Системные объекты, чтобы сделать обработку сигналов потоковой передачи в MATLAB.
Этот пример показывает, как к lowpass фильтруют сигнал с шумом в MATLAB и визуализируют исходные и отфильтрованные сигналы с помощью спектра анализатор.
Этот пример показывает, как к lowpass фильтруют сигнал с шумом в Simulink и визуализируют исходные и отфильтрованные сигналы со спектром анализатор.
Разработка и реализация фильтров в MATLAB и Simulink
Этот пример показывает, как разработать фильтры lowpass.
Этот пример показывает, как отфильтровать шумный сигнал щебета с фильтром lowpass, который имеет настраиваемую частоту полосы пропускания.
Многоскоростная обработка сигналов
Если вы используете R2016a или более ранний релиз, заменяете каждый вызов объекта с эквивалентным синтаксисом шага.
Ускорение алгоритма на десктопе
Спектральный анализ
Можно оценить передаточную функцию неизвестной системы на основе измеренных входных и выходных данных системы.
Вычислите спектрограмму и покажите эффект RBW на спектральных данных.
Визуализируйте и измеряйте сигналы
Этот пример показывает, как визуализировать и измерить сигналы во время и частотный диапазон в MATLAB с помощью осциллографа времени и спектра анализатор.
Получите данные об измерениях из dsp. Системный объект SpectrumAnalyzer
Получите данные об измерениях из блока Spectrum Analyzer
Создайте пользовательские алгоритмы
Этот пример показывает, как создать Систему object™, который реализует фильтр скользящего среднего значения.
Этот пример показывает, как создать Системный объект, состоявший из других Системных объектов.
Этот пример берет перспективу разработчика MATLAB, готового создать мгновенное средство оценки частоты на основе Дискретного энергетического Разделительного Алгоритма.
Развертывание
Этот пример показывает, как разработать фильтры для использования с входом фиксированной точки.
Этот пример показывает, как использовать MATLAB Compiler™, чтобы создать автономное приложение от функции MATLAB, которая использует Системные объекты от DSP System Toolbox™.
Этот пример показывает, как сгенерировать независимый исполняемый файл для потоковой передачи статистики с помощью MATLAB Coder™ и настроить сгенерированный исполняемый файл с помощью пользовательского интерфейса (UI), который запускается в MATLAB(TM).
Этот пример показывает, как смоделировать спецификацию алгоритма для трех параметрических эквалайзеров полосы, которые будут использоваться для генерации кода.
Этот пример демонстрирует, как сгенерировать HDL-код для программируемого КИХ-фильтра.
О системном моделировании DSP
Показывает, как сконфигурировать окружение Simulink для использования в моделях обработки сигналов
Сконфигурируйте окружение Simulink, чтобы минимизировать задержку и производительность симуляции увеличения
Сигнал переменного размера является сигналом, размер которого (число элементов в размерности) может измениться во время симуляции.
Обсуждает преимущества разработки фиксированной точки в целом и поддержки фиксированной точки в программном обеспечении System Toolbox, в частности, а также перечисляет распространенные приложения разработки обработки сигналов фиксированной точки
Документация
С DSP System Toolbox можно проектировать и анализировать КИХ, БИХ, многоскоростные, многоступенчатые, и адаптивные фильтры. Можно передать сигналы потоком от переменных, файлов данных и сетевых устройств для разработки системы и верификации. Time Scope, Спектр Анализатор и Logic Analyzer позволяют вам динамически визуализировать и измерить сигналы потоковой передачи. Для анализа прототипа и развертывания на встраиваемых процессорах, включая ARM ® Кора ® архитектуры, тулбокс поддерживает генерацию кода C/C++. Это также поддерживает побитовое моделирование фиксированной точки и генерацию HDL-кода от фильтров, БПФ, ОБПФ и других алгоритмов.
Алгоритмы доступны как функции MATLAB, Системные объекты и блоки Simulink.
Примеры
Потоковая обработка сигналов
В этом примере показано, как использовать Системные объекты, чтобы сделать обработку сигналов потоковой передачи в MATLAB®.
В этом примере показано, как к lowpass фильтруют сигнал с шумом в MATLAB® и визуализируют исходные и отфильтрованные сигналы с помощью спектра анализатор.
В этом примере показано, как отфильтровать низкие частоты в сигнале с шумом в Simulink и визуализировать исходный и отфильтрованный сигналы с помощью анализатора спектра.
Разработка и реализация фильтров в MATLAB и Simulink
В этом примере показано, как спроектировать фильтры lowpass.
В этом примере показано, как отфильтровать шумный сигнал щебета с фильтром lowpass, который имеет настраиваемую частоту полосы пропускания.
Многоскоростная обработка сигналов
В этом примере показано, как спроектировать фильтры для децимации и интерполяции дискретных рядов.
Выполните многоскоростную фильтрацию с помощью объектов преобразования уровня и блоков.
Ускорение алгоритма на десктопе
Спектральный анализ
Вычислите спектр мощности с помощью dsp.SpectrumAnalyzer и dsp.SpectrumEstimator Системные объекты.
Можно оценить передаточную функцию неизвестной системы на основе измеренных входных и выходных данных системы.
Вычислите спектрограмму и покажите эффект RBW на спектральных данных.
Визуализируйте и измеряйте сигналы
В этом примере показано, как визуализировать и измерить сигналы во время и частотный диапазон в MATLAB® с помощью осциллографа времени и спектра анализатор.
Получите данные об измерениях из dsp.SpectrumAnalyzer Системного объекта.
Получите данные об измерениях из блока Spectrum Analyzer.
Развертывание
В этом примере показано, как спроектировать фильтры для использования с входом фиксированной точки.
В этом примере показано, как использовать MATLAB Compiler™, чтобы создать автономное приложение от функции MATLAB, которая использует Системные объекты от DSP System Toolbox™.
В этом примере показано, как сгенерировать независимый исполняемый файл для потоковой передачи статистики с помощью MATLAB Coder™ и настроить сгенерированный исполняемый файл с помощью пользовательского интерфейса (UI), который запускается в MATLAB(TM).
В этом примере показано, как смоделировать спецификацию алгоритма для трех параметрических эквалайзеров полосы, которые будут использоваться для генерации кода.
В этом примере показано, как реализовать программируемый КИХ-фильтр для оборудования.
О системном моделировании DSP
Показывает, как сконфигурировать окружение Simulink для использования в моделях обработки сигналов.
Сконфигурируйте окружение Simulink, чтобы минимизировать задержку и эффективность симуляции увеличения.
Создайте сигнал переменного размера чей размер, изменение бегунка значений во время симуляции.
Обсуждает преимущества разработки фиксированной точки в целом и поддержки фиксированной точки в программном обеспечении System Toolbox, в частности, а также перечисляет распространенные приложения разработки обработки сигналов фиксированной точки.
Видео
Основанная на системе координат обработка в Simulink
Как обработать сигналы как системы координат в Simulink.
MATLAB+Simulink 8.0 (R2012b): пакет расширения Digital Signal Processing System Toolbox
Состав и назначение пакета расширения DSP System Toolbox
Пакет расширения DSP System Toolbox имеет обширный набор эффективных численных алгоритмов и инструментов для проектирования, анализа и блочного имитационного моделирования цифровых сигналов и систем общего применения. По принципу построения и применения он похож на пакет расширения Signal Processing Toolbox, легко с ним стыкуется и применяется при решении многих задач, например по проектированию сигналов, фильтров и радиоэлектронных устройств.
В то же время DSP System Toolbox — это особый пакет, вобравший в себя лучшие средства по работе с системами цифровой обработки сигналов и данных в составе базовой матричной системы MATLAB [2, 3] и основного пакета расширения ее по блочному имитационному моделированию Simulink [4]. DSP System Toolbox использует MATLAB функции и объекты, а также блоки моделей Simulink, добавляя к ним свои. Пакет поддерживает арифметику двойной точности с плавающей запятой и арифметику чисел с фиксированной запятой. Особенно много таких возможностей реализовано в разделах пакета, посвященных анализу и проектированию фильтров различного назначения.
На рис. 1 показано окно интерфейса MATLAB 8.0 с окном справки по пакету System Toolbox в правой части командного окна.
Рис. 1. Интерфейс MATLAB 8.0 с окном справки в правой части командного окна
Простые примеры применения DSP System Toolbox
Чтобы можно было отличить функции DSP System Toolbox от функций других пакетов, им присвоены названия в форме записей, например:
Здесь использована функция dsp.Convol-ver, демонстрирующая операцию свертки (рис. 2) именно в пакете DSD Toolbox. Команды выполняются в окне командного режима (признаком является MATLAB символ ввода «>>») (рис. 1). Результатом выполнения этих команд является окно с графиком свертки, показанное на рис. 1 слева внизу.
Рис. 2. Интерполяция с помощью функции dsp.Interpolator в программном режиме работы
Следующая программа выполняется из окна редактора программного кода и показывает проведение операции интерполяции двумя методами с помощью функции dsp.Interpolator:
Выполняется линейная интерполяция и с помощью специального фильтра с конечной импульсной характеристикой FIR. На рис. 2 показаны средства для програм-мной работы — редактор с листингом скрипта программы, командное окно и запуск с указанием имени файла dsp_demo.m этого примера. Также показано графическое окно с результатом работы программы.
Функции: оконные и создания сигналов
В последние годы в технике цифровой обработки информации широко применяются окна (windows). Например, в технике спектрального анализа окна предотвращают разрывы сигналов в начале и конце их временной области существования и уменьшают искажения спектра.
Пакет DSP Toolbox имеет очень удобную функцию dspWindows для представления различных окон (рис. 3):
Рис. 3. Функции окна Кайзера
Для просмотра передаточной характеристики окон во временной области и их спектра в частотной служит функция wvtool. Есть множество функций для создания и визуализации сигналов. Например, функция dsp.Chirp используется для создания сигнала «визг» с частотной модуляцией (рис. 4):
Рис. 4. Задание сигнала «визг» и его визуализация
Другая подобная функция — dsp.SineWave — позволяет задавать комплексные синусоидальные сигналы и разлагать их на действительную и мнимую компоненты. Она использована при анализе GSM цифрового понижающего конвертера (рис. 5). Здесь показано окно редактора с полным листингом программы, в которой заинтересованный пользователь может разобраться самостоятельно, и результаты вычислений — действительная и комплексная части выходного сигнала и их спектры, по виду очень напоминающие те, что были получены от обычных анализаторов спектра.
Рис. 5. Пример анализа GSM понижающего конвертера
По примерам применения этих функций несложно разобраться и с иными функциями такого рода.
Задание цифровых фильтров
Существует более 40 функций (в том числе входящих в MATLAB и используемых в других пакетах) для анализа и проектирования разнообразных дискретных (цифровых) фильтров. Относящиеся к DSP Toolbox функции имеют имена, как у записей:
создание адаптивного фильтра:
где [OP] — список выходных параметров; [IP] — список входных параметров.
В DSP Toolbox можно построить практически все известные виды фильтров [4] — резонансных, верхних и нижних частот, с конечной (FIR) и бесконечной (IIR) импульсной характеристикой, с различной архитектурой (например, эллиптические) и с особыми и заданными свойствами. Пример задания простого резонансного фильтра 2‑го порядка с бесконечной импульсной характеристикой IIR MATLAB (рис. 6) — функцией iirpeak — дает следующая простая программа:
Рис. 6. АЧХ и ФЧХ резонансного фильтра 2 го порядка
Другой пример иллюстрирует построение полосового фильтра с помощью функции пакета fdesign.bandpass, его спектра и АЧХ (рис. 7):
Рис. 7. Спектр сигнала и АЧХ полосового фильтра
Ряд функций предназначен для задания адаптивных и неадаптивных фильтров, ослабляющих шумы сигналов. В представленном далее примере показано, как создаются сигнал с шумом и адаптивный фильтр для его ослабления и строятся временные диаграммы сигнала на входе и выходе фильтра (рис. 8):
Рис. 8. Сигналы на входе (синий) и выходе (красный) адаптивного фильтра, ослабляющего шум
Применение операций Fixed Point
Принципиально важной особенностью пакета DSP System Toolbox является возможность поддержки арифметических операций с фиксированной точкой (Fixed Point). Обычно используются операции с плавающей точкой и двойной разрядностью. Они выполняют вычисления с высокой точностью, но с невысокой скоростью.
Применение арифметики с фиксированной точкой позволяет уменьшить разрядность чисел и повысить скорость вычислений, которые часто выполняются на аппаратном уровне компьютера. Кроме того, в такой арифметике используются специальные ускоренные алгоритмы вычислений и специальные меры по уменьшению ошибок вычислений.
На рис. 9 приведен пример работы с Fixed Point арифметикой при построении FIR-фильтра прямой формы. Показаны окно редактора с листингом программы, окно командного режима с отчетом по Fixed Point вычислениям, АЧХ фильтров разного порядка и графики временной зависимости выходного сигнала при вычислениях с плавающей и с фиксированной точкой.
Рис. 9. Пример построения в MATLAB FIR-фильтра прямой формы с использованием арифметики чисел с фиксированной точкой
Пакет DSP System Toolbox имеет свыше десятка функций реализации фильтров с Fixed Point арифметикой. Они подобны аналогичным функциям для фильтров на основе арифметики чисел с плавающей точкой — Floating Point, но характеристики фильтров, естественно, несколько отличаются. Имеются соответствующие функции преобразования данных в формате Fixed Point в формат Floating Point и наоборот.
Инструмент визуализации фильтров fvtool
Для построения амплитудно-частотных и других характеристик фильтров в DSP Toolbox и Signal Processing System используется специальный инструмент визуализации фильтров — fvtool. Его можно вызвать указанием имени с пустым GUI-окном, а можно заранее задать фильтры. В приведенной ниже программе заданы два FIR-фильтра и в окне fvtool построены их АЧХ и ФЧХ (рис. 10):
Рис. 10. Окно инструмента визуализации фильтров fvtool c AЧХ и ФЧХ двух FIR-фильтров и открытой позицией меню анализа
Еще один пример получения АЧХ и ФЧХ фильтров (рис. 11) дает следующая программа:
Рис. 11. Окно fvtool с АЧХ и ФЧХ разных фильтров
Большим ослаблением в зоне затухания отличаются цифровые эллиптические фильтры высокого порядка. Они также могут давать «равноволновость» в полосах частот пропускания и затухания. Следующая программа иллюстрирует построение АЧХ и ФЧХ двух таких фильтров (рис. 12):
Рис. 12. АЧХ и ФЧХ двух эллиптических НЧ-фильтров с минимальным ослаблением 60 и 80 дБ
ФЧХ этих фильтров практически линейны, что указывает на постоянство частоты групповой и фазовой задержек. Инструмент fvtool позволяет в интерактивном режиме выполнить полный анализ фильтров. Виды анализа представлены в открытой позиции меню Analysis (рис. 10). Он включает в себя, помимо анализа АЧХ и ФЧХ, а также групповой и фазовой задержек, расчет и построение переходных и импульсных характеристик (рис. 13).
Рис. 13. Переходные характеристики двух НЧ эллиптических фильтров с минимальным ослаблением 60 и 80 дБ (левый рисунок) и их импульсные характеристики (правый график)
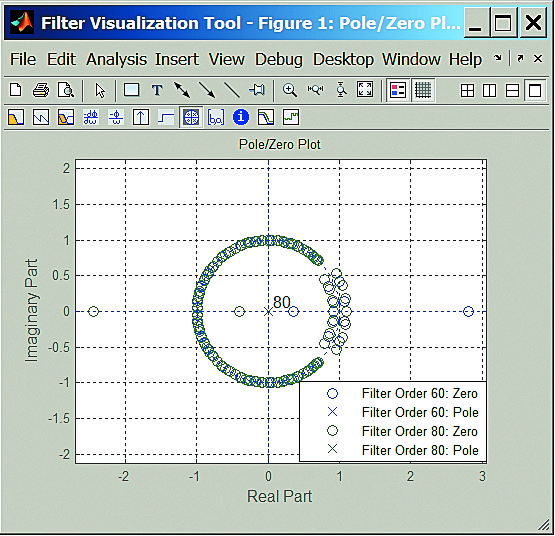
Переходная характеристика является реакцией фильтра на единичный скачок, а импульсная — на импульс с единичной площадью и длительностью, стремящейся к нулю (рис. 14). (Это значит, что амплитуда такого импульса стремится к бесконечности.) Эти характеристики помогают понять поведение фильтров во временной области. Кроме того, можно получить на комплексной плоскости нули и полюсы передаточной характеристики фильтров.
Рис. 14. Нули и полюсы двух НЧ эллиптических фильтров с минимальным ослаблением 60 и 80 дБ
Задание фильтров с помощью инструмента filterbuilder
В приведенных примерах подлежащие конструированию и анализу фильтры были явно указаны их функциями. Пакет расширения имеет инструмент для задания фильтров, генерирующий нужные функции при определенных свойствах проектируемых фильтров. Он вызывается в командном режиме MATLAB командой:
При этом появляется небольшое окно Response (рис. 15) со списком типов фильтров. Оно имеет GUI-интерфейс. Выбрав тип фильтра (в данном примере — полосовой фильтр), нужно нажать кнопку ОК. Появится окно уточненного задания типа фильтра, показанное на рис. 15 справа. В нем можно уточнить параметры проектируемого фильтра и просмотреть его передаточную характеристику, активизировав кнопку View Filter Response: она показана на рис. 15 снизу в левой части окна MATLAB командного режима.
Рис. 15. Инструменты конструирования заданного типа фильтра
Теперь, нажав кнопку ОК конструктора, можно получить в командном окне следующее текстовое сообщение:
Исполнив команду Hpp (или иную из сообщения), получим:
Таким образом, заданный фильтр полностью определен, и для получения его детальных характеристик следует воспользоваться инструментом fvtool, который описан ранее.
Дискретные преобразования сигналов
В пакет DSP Toolbox входит пять функций дискретного преобразования — прямого и обратного косинусных преобразований, прямого и обратного преобразований Фурье и функция представления аналитических сигналов. Косинусные преобразования широко применяются в технике компрессии и декомпрессии сигналов, а преобразования Фурье лежат в основе спектрального анализа. Учитывая теоретическую и практическую важность функций преобразования, рассмотрим примеры применения их всех.
В следующем примере вначале создается двухкомпонентный сигнал, содержащий линейную и синусоидальную компоненты, потом он подвергается прямому косинусному преобразованию (функция dsp.DCT), а затем обратному косинусному преобразованию (функция dsp.ISCT):
В промежутке между преобразованиями малые значения результатов прямого преобразования удаляются, что обеспечивает компрессию сигнала. Тем не менее реконструкция сигнала дает очень близкие значения сигнала, что показано на рис. 16.
Рис. 16. Косинусное дискретное преобразование сигнала и его реконструкция
Прямое дискретное быстрое преобразование Фурье — «рабочая лошадка» в спектральном представлении сигналов в частотной области. Это наглядно иллюстрирует следующая программа, создающая зашумленный сигнал из двух синусоид с разной амплитудой и частотой, а затем строящая его спектр (рис. 17) с помощью функции прямого БПФ dsp.FFT:
Рис. 17. Спектр зашумленного двухкомпонентного сигнала
БПФ — особый быстрый алгоритм преобразования Фурье. Он резко ускоряет преобразования, но совершенно не меняет их суть и конечные результаты.
Следующая программа показывает совместное действие прямого и обратного преобразования Фурье:
Программа выдает результат:
Это норма разности исходного и преобразованного сигнала. А это значит, что произошло практически полное восстановление сигнала с точностью машинных вычислений.
Наконец, еще одна программа:
дает разложение аналитического сигнала — синусоиды — на его действительную и мнимую части (рис. 18).
Рис. 18. Синусоидальный сигнал и его действительная и мнимая части
Заметим, что в DSP Toolbox можно работать и с рядом подобных MATLAB-функций, применяемых в других пакетах расширения и описанных в них.
Библиотека Simulink-блоков пакета расширения DSP Toolbox
Большинство задач анализа и проектирования систем с цифровой обработкой сигналов можно решать на уровне программирования в MATLAB и пакетах расширения, особенно в направленном на это пакете DSP Toolbox. Однако разработчики этого пакета пошли дальше: большинство его функций создано не столько для самостоятельного применения, сколько для поддержки универсальных приложений с GUI-интерфейсом и обеспечения блочного имитационного моделирования на базе основного пакета расширения Simulink. Необходимая для этого библиотека блоков моделей была включена в пакет DSP Toolbox.
На рис. 19 показано основное окно библиотеки блоков Simulink. В левой его части находится дерево разделов библиотеки, открытое на разделах, относящихся к пакету расширения DSP Toolbox. В окне с золотистыми пиктограммами представлены пиктограммы разделов библиотеки этого пакета. Приведены также окна с блоками моделей.
Рис. 19. Окно библиотеки Simulink и первая группа окон библиотеки пакета DSP Toolbox
Каждый блок имеет наглядное обозначение в виде пиктограммы и имя. Например, в блоках спектрального анализа пиктограммы представляют собой типичный вид спектра, в математических блоках — названия математических функций и т. д. Для определения отличных от заданных по умолчанию параметров блоков служат окна установки параметров, которые вызываются двойным щелчком мыши на пиктограмме блока.
Вторая группа окон с блоками моделей показана на рис. 20. Здесь представлены блоки с функциями преобразования (окно Transform), источниками сигналов (Source), средствами отображения и визуализации сигналов (Sinks), буферами (Buffers) и др.
Рис. 20. Вторая группа окон библиотеки пакета DSP Toolbox
Третью группу окон с блоками моделей можно видеть на рис. 21. Здесь представлены блоки фильтров различного типа и назначения. В окне с золотистыми прямоугольниками расположены разделы библиотеки фильтров.
Рис. 21. Третья группа окон библиотеки пакета DSP Toolbox
В целом библиотека блоков моделей пакета DSP Toolbox весьма обширна, что говорит о множестве систем и устройств цифровой обработки сигналов, которые можно моделировать с ее помощью. Каждая моделируемая система (или каждое устройство) должна быть представлена диаграммой своей модели, составленной из нужных блоков и соединений между ними. Необходимо учитывать тип блоков и формат передаваемых сигналов: некоторые блоки разных пакетов расширения могут совпадать по функциональному назначению, но отличаться форматами передачи данных (на это указывает вид портов блоков). Подобные блоки рассматриваются как разные, так как они не могут соединяться друг с другом.
Диаграммы моделей создаются переносом мышью блоков их окон в окно диаграммы (открывается командой New в меню File основного окна библиотеки Simulink — рис. 19). Возможна также (командой Open) загрузка готовых диаграмм, например демонстрационных примеров. Блоки на диаграмме соединяются с помощью мыши. Детали подготовки диаграмм описаны в [4].
Применение блоков осциллографа и анализатора спектра
На рис. 22 показана диаграмма простейшей модели, иллюстрирующей применение виртуального осциллографа для наблюдения сигналов из рабочего пространства — прямо и после фильтрации цифровым фильтром. Справа от диаграммы расположено окно осциллографа с наблюдаемыми графиками временной зависимости сигналов. Модель запускается кнопкой с треугольником в кружке. В процессе выполнения диаграммы панель инструментов с этой кнопкой выводится тусклой.
Рис. 22. Диаграмма модели, иллюстрирующая применение виртуального осциллографа для наблюдения сигналов во временной области
Каждый блок имеет окно параметров — это блок параметров осциллографа над осциллограммами. Он выводится двойным щелчком правой клавиши мыши. Часто для правильной работы диаграммы достаточно установок параметров по умолчанию, но в общем случае их установка выполняется в процессе отладки работы диаграммы. Тогда же определяются и общие параметры моделирования — тип решателя, шаг решения, начальное и конечное время моделирования и т. д.
Следующая диаграмма (рис. 23) иллюстрирует применение виртуального анализатора спектра, на вход блока которого подан сигнал — прямо от виртуального генератора и через цифровой фильтр. Спектр сигнала показан на рис. 23 справа от диаграммы. Представлено также окно параметров анализатора спектра.
Рис. 23. Диаграмма модели, иллюстрирующей применение виртуального анализатора спектра в частотной области
DSP Toolbox можно использовать для сравнения методов спектрального анализа с применением окон различного типа (рис. 24). Тут в одной диаграмме выполняется спектральный анализ тремя методами и на одном графике строятся все четыре спектра. Это позволяет их сравнивать.
Рис. 24. Диаграмма модели, иллюстрирующей три метода анализа спектра
Диаграмма модели системы, осуществляющей спектральную компрессию сигнала, показана на рис. 25. Компрессия осуществляется за счет устранения высших гармоник спектра сигнала с малой энергией.
Рис. 25. Диаграмма модели спектральной компрессии
Для наблюдения нестационарных сигналов в канале связи можно использовать диаграмму, приведенную на рис. 26.
Рис. 26. Диаграмма модели наблюдения нестационарных сигналов в канале связи
Уже отмечалось широкое применение в пакете расширения DSP Toolbox адаптивных методов очистки сигналов от шума. Еще одна реализация такого метода представлена на рис. 27. Здесь использован RLS-фильтр, использующий метод наименьших квадратов. Эффективность очистки на примере синусоидального сигнала иллюстрируется осциллограммами виртуального осциллографа.
Рис. 27. Диаграмма модели адаптивной очистки от шума
Окно блока параметров фильтра Notice Filter представлено на рис. 28. Используется фильтр типа FIR прямой формы 31‑го порядка.
Рис. 28. Окно блока параметров фильтра
Моделирование DSP для обработки аудиосигналов
Эквалайзеры, корректирующие АЧХ, широко применяются в электроакустике. В DSP Toolbox имеется модель трехполосного параметрического эквалайзера. Диаграмма на рис. 29 поясняет его работу и формирование результирующей АЧХ путем изменения центральной частоты и высоты пика каждой полосы.
Рис. 29. Диаграмма модели параметрического акустического эквалайзера
Рис. 30. Диаграмма контроля MIDI-сигналов
Звуковая система каждого современного компьютера содержит синтезатор музыкальных звуковых сигналов — MIDI-синтезатор. Диаграмма, показанная на рис. 30, позволяет контролировать и наблюдать сигналы от MIDI-синтезатора.
В компьютеры часто встраивают звуковые карты, поддерживающие многоканальное воспроизведение звуков, подобное тому, что применяется в домашних кинотеатрах. Особенность таких систем — в возможности определения направления на звук объекта звучания. Диаграмма на рис. 31 моделирует работу домашнего кинотеатра с пятью колонками (одна центральная и по две фронтальные и тыловые) и позволяет оценить положение источника звука — вертолета — относительно человека, находящегося в центре домашнего кинотеатра. Звук должен идти примерно с того места, куда мышкой помещен вертолет.
Рис. 31. Диаграмма моделирования домашнего кинотеатра
При изучении реальных стереосигналов весьма полезны представления в виде периодограмм и особенно спектрограмм в плоскости амплитуда-частота-время. Диаграмма на рис. 32 иллюстрирует получение этих характеристик. Они позволяют оценить степень стереоэффекта и «прозрачность» звука.
Рис. 32. Диаграмма, иллюстрирующая получение периодограммы и спектрограммы аудиосигнала
Ослабление шума — одна из наиболее часто встречаемых задач цифровой обработки аудиосигналов. На рис. 33 приведена диаграмма модели одной из цифровых систем шумоподавления акустических сигналов. При наличии у компьютера звуковой карты и акустической системы степень подавления шума можно проверить, используя прямоугольные кнопки под диаграммой. Трехмерная диаграмма показывает развитие спектра во времени в процессе адаптации системы.
Рис. 33. Диаграмма подавителя акустических шумов
В последнее время в аппаратные средства связи и вычислительной техники внедряются цифровые методы анализа и синтеза речи. Диаграмма на рис. 34 иллюстрирует моделирование одной из таких систем с линейным кодированием и предсказанием (LPC). Здесь также можно проверить качество синтеза речи, используя кнопки под диаграммой.
Рис. 34. Диаграмма LPC анализа и синтеза речи
Применение блоков математических операций
В DSP Toolbox представлены также блоки математических операций. Их можно использовать при блочном имитационном моделировании различных устройств. Например, на рис. 35 приведена диаграмма, выделяющая нули магнитуды АМ-сигнала двумя способами. Результаты получаются практически идентичными.
Рис. 35. Диаграмма модели выделения пересечений магнитуды сигнала через нуль
Быстрое (в динамике процесса) проведение полиномиальной регрессии для множества кадров изменяющихся данных (точек) иллюстрирует диаграмма, показанная на рис. 36. На ней показана регрессия для конечного кадра.
Рис. 36. Диаграмма полиномиальной регрессии
Примеры моделирования связных и радиолокационных устройств
Для моделирования коммуникационных устройств с MATLAB поставляется пакет расширения Communication Systems Toolbox. Однако для моделирования некоторых устройств набор блоков в пакете DSP Toolbox может оказаться более предпочтительным. Рассмотрим несколько таких примеров.
Диаграмма на рис. 37 иллюстрирует проведение однополосной амплитудной модуляции и представление ее спектров. Удаление одной из боковых полос сужает спектр сигнала вдвое и позволяет в системах связи увеличить отношение сигнал/шум.
Рис. 37. Диаграмма системы однополосной модуляции и ее спектры
Одним из популярных видов модуляции импульсных сигналов является дельта-модуляция. Диаграмма на рис. 38 позволяет моделировать и сравнивать три вида дельта-модуляции: LDM, CVSD и ADPCM. Во всех случаях использованы кодеки и декодеки для соответствующего вида модуляции.
Рис. 38. Диаграмма моделирования трех видов дельта-модуляции
Диаграмма на рис. 39 иллюстрирует получение изображения на экране трубки радара. Для обработки изображения с целью повышения точности индикации используется фильтр Калмана, выполненный в виде полусистемы (субблока).
Рис. 39. Диаграмма модели системы индикации радара с фильтром Калмана
Для повышения точности оценки апертуры радаров применяется метод SAR (Synthetic Aperture Radar Processing). Диаграмма его реализации показана на рис. 40. Суть метода представлена с помощью спектрограммы и звездных диаграмм. Их окна находятся под диаграммой модели.
Рис. 40. Диаграмма, иллюстрирующая метод SAR при работе радара
Заключение
Новый пакет расширения DSP Toolbox 6.3, разработанный для матричной системы MATLAB+Simulinl 8/0 (R2012b), содержит многочисленные средства (в том числе Simulink-блоки моделей) разных компонентов для построения, проектирования, анализа и имитационного моделирования разнообразных систем и устройств с цифровой обработкой сигналов. Таким образом, MATLAB+Simulink 8.0 (R2012b) стала одной из первых перспективных систем для проектирования и моделирования современных устройств и систем с цифровой обработкой информации. Ее возможности по моделированию генераторов, модуляторов, демодуляторов и т. д., а также по представлению и индикации сигналов позволяют выполнять в этой системе широкий спектр работ по проектированию, анализу и имитационному моделированию систем с DSP.