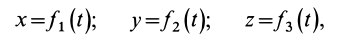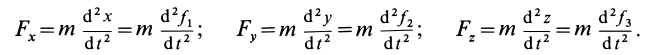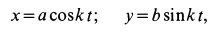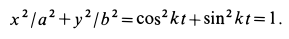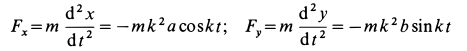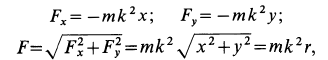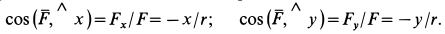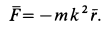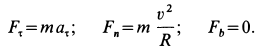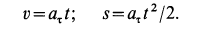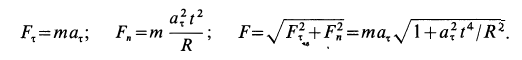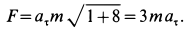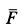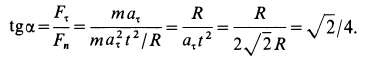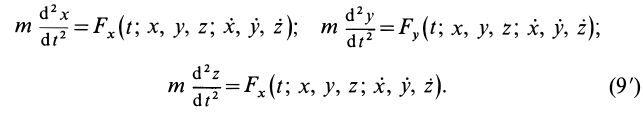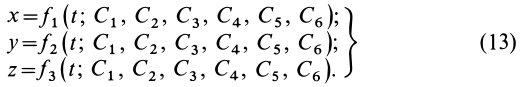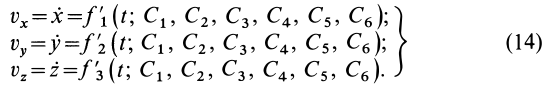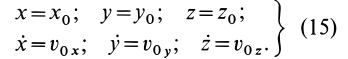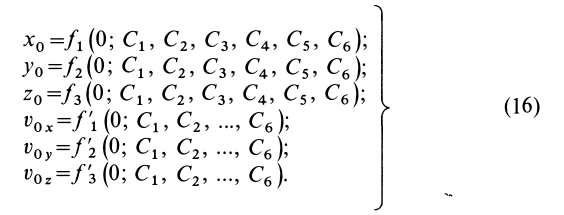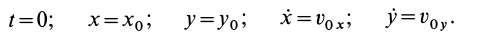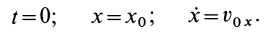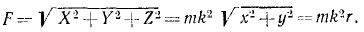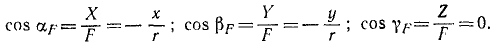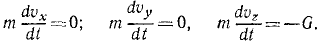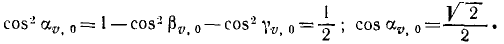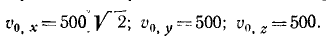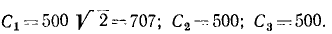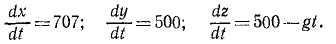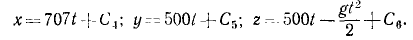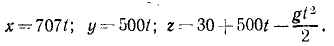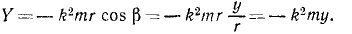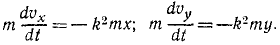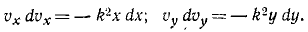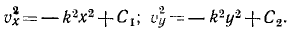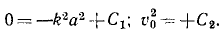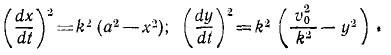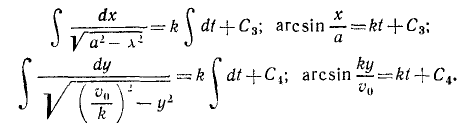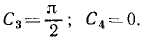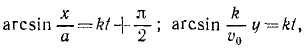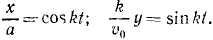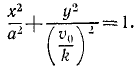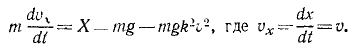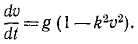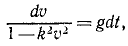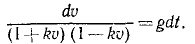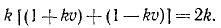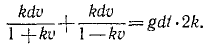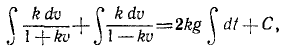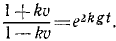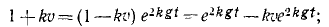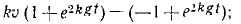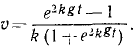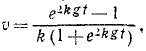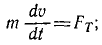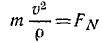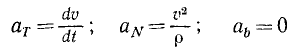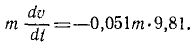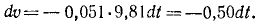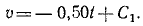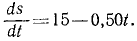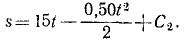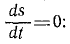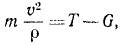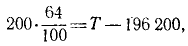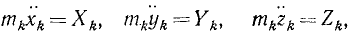Две материальные точки движутся в плоскости так что координаты первой точки

Две материальные точки движутся в плоскости так что координаты первой точки

Условие и решение задач

1. Координата x движущейся частицы меняется позакону x = A cos(2pt/T), А= 8 см. Найти выражения для проекций на ось x скорости v и ускорения a частицы, составляющую v_x средней скорости частицы на интервале времени от t₁ = 0 до t₂= T/8.
→ Перейти к решению задачи

4. Радиус-вектор,определяющий положение движущейся частицы меняется по закону r =3t 2 i + 2t j + k, где i, j, k орты осей x, y, z. Найти модуль скорости v в момент времени t = 1 с.
→ Перейти к решению задачи

7. В момент t = 0 частица вышла из начала координат в положительном направлении оси х. Ее скорость меняется со временем по закону v = v₀ (1 — t/τ), где v₀ — вектор начальной скорости, модуль которого v₀=10,0 см/с, τ = 5,0 с. Найти координату x частицы в моменты времени 6,0, 10 и 20 с.
→ Перейти к решению задачи

10. Материальная точка движется в плоскости x0y по закону x = Asinwt,y = A(1+coswt),где A и w положительные константы. Найдите уравнение кривой, описывающей траекторию частицы, изобразите ее вид и направление движения частицы.
→ Перейти к решению задачи

12. С вышки бросили камень в горизонтальном направлении. Через t=4 с камень упал на землю на расстоянии L = 40 м от основания вышки. Определите начальную v₀ и конечную v_f скорости камня.
→ Перейти к решению задачи

13. Камень брошен со скоростью v₀ = 30 м/с под углом 60 0 кгоризонту. Определите радиус кривизны траектории в верхней ее точке.
→ Перейти к решению задачи

14. Шарик падает с нулевой начальной скоростью на гладкую наклонную плоскость, составляющую угол α с горизонтом. Пролетев расстояние h, он упруго отражается от плоскости. На каком расстоянии от места падения шарик отразится второй раз?
→ Перейти к решению задачи

15. На гладкую горизонтальную плоскость помещены три тела массами т₁, т₂ и т₃,связанные нитями между собой и с телом массой М, привязанное к нити, перекинутой через блок. Найтиускорение а системы. Найти натяжениявсех нитей. Трением в блоке, массами блоков и нитей пренебречь.
→ Перейти к решению задачи

17. Движущаяся частица претерпевает упругое соударение с покоящейся частицей такой же массы. Доказать, что после столкновения, если оно не было центральным, частицы разлетятся под прямым углом друг к другу. Как будут двигаться частицы после центрального соударения?
→ Перейти к решению задачи

20. Диск вращается вокруг неподвижной оси так, что его координата определяется уравнением φ = 0,5t 2 (рад). Найдите касательное ускорение его точек, отстоящих от оси вращения на 80 см.
→ Перейти к решению задачи

22. Частица движется по окружности радиусом 2 см, при этом зависимость ее пути от времени задана уравнением s = 0,1 t 3 (см). Найдите касательное ускорение частицы в тот момент времени, когда ее линейная скорость стала 0,3 м/с.
→ Перейти к решению задачи

24. Нормальное ускорение частицы, движущейся по окружности радиусом 4 м, задается уравнением а_n = 1 + 6t + 9t 2 (м/с 2 ). Вычислите касательное ускорение частицы через 1 с после начала движения.
→ Перейти к решению аналогичной задачи

25. Диск вращается вокруг неподвижной оси так, что его угловая координата определяется уравнением φ = 0,5 t 2 (рад). Вычислите полное ускорение точек, отстоящих от оси вращения на 80 см к концу второй секунды движения.
→ Перейти к решению задачи

26. Колесо радиусом 10 см вращается так, что линейная скорость точек на его ободе задана уравнением v= 3t+ t 2 (см/с)Найдите угол между вектором полного ускорения и радиусом колеса спустя 1 с после начала движения.
→ Перейти к решению задачи

35. Модуль импульса частицы массой 2 кг изменяется по закону р = 10 Cos πt (кгм/с). В начальный момент времени радиус-вектор частицы равен нулю. Найдите модуль радиус-вектора частицы через 1/3 секунды.
→ Решение отсутствует / Предложить свой вариант решения

36. Если путь частицы массой 2кг изменяется по закону s = 5 Sin πt (см). Найдите ближайший момент времени от начала еедвижения, когда модуль импульса частицы становится максимальным.
→ Перейти к решению задачи

38. Частица массой 1 кг в начальный момент времени имеет радиус-вектор r₀ = 2 i+ 3 j, где i, j орты осей x, y. На нее действует сила F= 1,5y 2 i+ 3x 2 j – 0,2(x 2 +y 2 )k. Найдите модуль этой силы в начальный момент времени.
→ Перейти к решению задачи

39. Десять шариков массами 100 г, 200 г, …,1000 г укреплены в указанном порядке на невесомом стержне длиной 90 см. На каком расстоянии от центра самого легкого шарика будет находиться центр масс системы, если расстояние между соседними шариками 10 см?
→ Перейти к решению задачи

40. В двух вершинах равностороннего треугольника помещены шарики с массами m каждый, а в третьей вершине – с массой 2m. Где будет находиться центр масс данной системы.
→ Перейти к решению задачи

41. Автобус массой 5 т начинает двигаться от остановки так, что его скорость в зависимости от пройденного пути изменяется по закону v = √ s (м/с). Найдите суммарную работу всех сил, действующих на автобус за первые 15 с от начала движения.
→ Перейти к решению задачи

42. Воздушный поток (ρ = 1,29 кг/м 3 ) сечением 0,55 м 2 имеет скорость 20м/с. Чему будет равна мощность этого потока?
→ Перейти к решению задачи

44. Шар массой 2 кг движется со скоростью 8 м/с и догоняет шар массой 3 кг, который движется со скоростью 4 м/с. Найдите работу деформации шаров при их центральном неупругом ударе.
→ Решение отсутствует / Предложить свой вариант решения

45. В боковой поверхности сосуда с жидкостью,стоящего на горизонтальной плоскости, имеется малое отверстие. Высота неизменного уровня жидкости над этим отверстием составляет 36 см, а расстояние от отверстия до дна сосуда 144 см. Найдите дальность горизонтального полета струи жидкости из этого отверстия.
→ Решение отсутствует / Предложить свой вариант решения

49. Материальная точка движется в плоскости x0y по закону x = Asinwt,y = Bcoswt,где A, B и w положительные константы, A = B = 5 cм. Найдите уравнение кривой,описывающей траекторию частицы, изобразите ее вид и направление движения частицы.
→ Перейти к решению задачи

50. Материальная точка движется по дуге окружности радиуса R по закону L = A sinwt,где L смещение из начального положения, отсчитываемое вдоль дуги, A и w положительные константы. Найдите полное ускорение частицы в точке L = 0.
→ Перейти к решению задачи

55. Частица движется по окружности радиуса R = 15см с постоянным тангенциальным ускорением a_t. Найдите это ускорение, еслиизвестно, что к концу пятого оборота после начала движения скорость частицы стала равной v = 79.2 см/с.
→ Перейти к решению задачи

57. Найти работу, которую нужно совершить, чтобы увеличить скорость движения тела от v₁= 2 м/с до v₂= 6 м/с на пути s = 15 м. На всем пути действуетпостоянная сила трения F_тр=2 Н. Масса тела m = 1 кг.
→ Перейти к решению задачи

58. Находясь под действием постоянной силы с компонентами (3, 10, 8) Н частица переместилась из точки 1 с координатами (1, 2, 3) м в точку 2 с координатами (3, 2, 1) м. Какая совершилась при этом работа? Как изменилась кинетическая энергия частицы?
→ Перейти к решению задачи

60. Лодка длиной L₀ наезжает,двигаясь по инерции, на отмель и останавливается из-за трения, когда половина ее длины оказывается на суше. Какова была начальная скорость лодки v? Коэффициент трения равен μ.
→ Решение отсутствует / Предложить свой вариант решения

61. Лодка массы М с находящимся в ней человеком массы т неподвижно стоит на спокойной воде. Человек начинает идти вдоль по лодке со скоростью u относительно лодки. С какой скоростью w будет двигаться человек относительно воды? С какой скоростью v будет при этом двигаться лодка относительно воды? Сопротивление воды движению лодки не учитывать.
→ Перейти к решению задачи

62. Человек прошел вдоль по лодке, описанной в предыдущей задаче, путь l. Каковы при этом будут смещения лодки S₁ и человека S₂ относительно воды?
→ Перейти к решению задачи

63. Две пружины жесткостью 4×10 2 Н/м и 6×10 2 Н/м соединены последовательно. Определить работу по растяжению обеих пружин, если вторая пружина растянута на 3 см. Определить также коэффициент жесткости системы двух пружин.
→ Перейти к решению задачи

64. Математический маятник (груз малых размеров налегком подвесе длиной l) находится вположении равновесия. Определить какую минимальную скорость u надо сообщить грузу, чтобы он мог совершить полный оборот, для двух случаев: а) груз подвешен на жестком стержне; б) на нити.
→ Перейти к решению задачи

65. Два идеально упругих шарика массами m₁ и m₂ вдоль одной и той же прямой со скоростями v₁ и v₂. Во время столкновения шарики начинают деформироваться, и часть кинетической энергии переходит в потенциальную энергию деформации. Затем деформация уменьшается, и запасенная потенциальная энергия вновь переходит в кинетическую. Найти значение потенциальной энергии деформации в момент, когда она максимальна.
→ Перейти к решению задачи

67. Два шарика падают в воздухе. Шарики сплошные, сделаны из одного материала, но диаметр одного из шариков вдвое больше другого. В каком соотношении будут находиться скорости шариков при установившемся (равномерном) движении? Считать, что сила сопротивления воздуха пропорциональна площади поперечного сечения движущегося тела и квадрату его скорости.
→ Перейти к решению задачи

70. Железный шарик (ρ = 7900 кг/м 3 ) диаметром 5 мм падает в касторовом масле ( ρ = 900 кг/м 3 | ŋ = 1 Пас). Вычислите число Рейнольдса при установившемся движении шарика.
→ Перейти к решению задачи

Источник

Две материальные точки движутся в плоскости так что координаты первой точки

Лифт поднимается с ускорением 1.2м/с2 высота лифта 2.7м, при подъеме сверху падает болт(V0 =0), какое время болт будет находиться в полете? Ответ 0,7

решение:
S=V0t+at^2/2
S=at^2/2
a=g+aл (ал ускорение лифта)
t^2=2S/a
t^2=5,4/11,2
t=0,694=0.7

Мне кажется что тут так получится tсв=корень квадратный дроби, в числителе 2h, а в знаменателе aл(ускор.лифта) + g. Хотя ответ от этого не меняется) возможно это другое решение)))

PashOK>> У меня решение это препод проверял
>>ну а ты покажи ему моё решение и напишешь правильное ли оно? ок

Расстояние равно 150км, катер двигаясь по течению затратил 2 часа, а против течения 3 часа, найдите скорость катера в стоячей воде? ответ: 62,5

решение:
(Vk-скорость катера Vt-скорость течения t1=2-время по течению t2=3-время против течения)
Vk+Vt=S/t1
Vk-Vt=S/t2

PashOK>> Ответ точно верный

PashOK>> Ответ точно верный

еще был вопрос что такое материальная точка, желательно повторить

PashOK>> Ответ в тесте был под номером 5ть

t^5, а модуль нормального ускорения an

t^k. Найти вот эту k и записать
кто решил и уверен в своём ответе, пишите!
что то связанно с производной, вроде там k=3

Пусть r-радиус вектора частицы движущееся в плоскости XY. Что можно сказать о её траектории, если r меняется только по модулю, не меняя направления на противоположное? Частица может двигаться(варианты ответов) там частица проходит через начало координат и там движется, там вроде только один вариант ответа с прохождением начала координат!

PashOK>> через начала координат там 2 ответа, короч друг пролетел на этой задаче
>>Ну и? какие варианты ответов? считай уже знаешь что через начало координат и там дальше не тяжело, как я помню вдоль по оси oX. Я вот пролетел, но у меня не было инфы что через начало.

Источник

Две основные задачи динамики точки в теоретической механике

Содержание:

Две основные задачи динамики точки:

Используя дифференциальные уравнения движения материальной точки в. той или другой системе координат, можно решать две основные задачи динамики точки.

Первая задача

Зная массу точки и ее закон движения, можно найти действующую на точку силу. Действительно, если, например, заданы уравнения движения точки в декартовой системе координат

то проекции силы на оси координат определяются из дифференциальных уравнений движения точки (9), т. е.

Зная проекции силы на координатные оси, легко определить модуль силы и косинусы углов силы с осями координат.

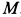
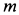
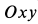
Пример 1. Точка , имеющая массу (рис. 5), движется в плоскости так, что уравнениями ее движения являются

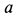
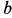
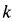
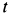
где , , — постоянные положительные величины; — время.

Определить силу, под действием которой точка совершает это движение.

Решение. Найдем уравнение траектории точки в координатной форме, исключая время из уравнений движения:

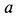
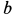
Траекторией точки является эллипс с полуосями и .

Рис. 5

На основании дифференциальных уравнений движения точки (10)

или, если ввести координаты движущейся точки,

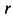
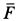
где —радиус-вектор движущейся точки. Косинусы углов силы с осями координат

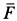
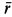
Отсюда можно заключить, что сила имеет направление, противоположное радиусу-вектору . Окончательно

Рис. 6

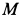
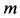
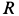
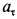
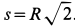
Пример 2. Точка , имеющая массу (рис. 6), движется из состояния покоя по окружности радиусом с постоянным касательным ускорением . Определить действующую на точку силу в момент, соответствующий пройденному точкой по траектории расстоянию .

Решение. Применяя дифференциальные уравнения движения точки в проекциях на естественные оси, имеем:

Так как движение происходит с постоянным касательным ускорением 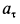без начальной скорости, то

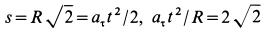
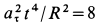
В момент, когда и, следовательно, ,

Тангенс угла 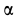между радиусом окружности и силой

Из рассмотрения первой задачи динамики точки видно, что по заданной массе точки и уравнениям ее движения сила полностью определяется как по величине, так и по направлению.

Вторая задача

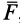
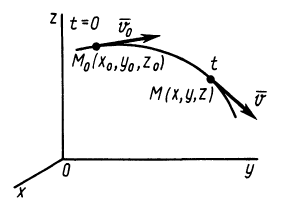
По заданной массе и действующей на точку силе необходимо определить движение этой точки. Рассмотрим решение этой задачи в прямоугольной декартовой системе координат. В общем случае сила , а следовательно, и ее проекции на координатные оси могут зависеть от времени, координат движущейся точки, ее скорости, ускорения и т. д. Для простоты ограничимся случаем зависимости силы и ее проекций на оси координат от времени, координат и скорости. Дифференциальные уравнения движения точки (9) имеют вид

Для нахождения уравнений движения точки в декартовых координатах необходимо проинтегрировать систему трех обыкновенных дифференциальных уравнений второго порядка. Из теории обыкновенных дифференциальных уравнений известно, что решение одного дифференциального уравнения второго порядка содержит две произвольные постоянные. Для случая системы трех обыкновенных дифференциальных уравнений второго порядка имеется шесть произвольных постоянных: .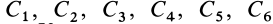

Каждая из координат 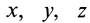движущейся точки после интегрирования системы уравнений (9) зависит от времени t и всех шести произвольных постоянных, т. е.

Если продифференцировать уравнения (13) по времени, то определяются проекции скорости точки на координатные оси:

Таким образом, задание силы не определяет конкретного движения материальной точки, а выделяет целый класс движений, характеризующийся шестью произвольными постоянными. Действующая сила определяет только ускорение движущейся точки, а скорость и положение точки на траектории могут зависеть еще от скорости, которая сообщена точке в начальный момент, и от начального положения точки. Так, например, материальная точка, двигаясь вблизи поверхности Земли под действием силы тяжести, имеет ускорение 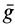, если не учитывать сопротивление воздуха. Но точка будет иметь различные скорости и положение в пространстве в один и тот же момент времени и различную форму траектории в зависимости от того, из какой точки пространства началось движение и с какой по величине и направлению начальной скоростью.

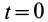
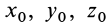
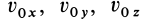
Для выделения конкретного вида движения материальной точки надо дополнительно задать условия, позволяющие определить произвольные постоянные, которых в общем случае будет шесть. В качестве таких условий обычно задают так называемые начальные условия, т.е. в какой-то определенный момент времени, например при (рис. 7), задают координаты движущейся точки и проекции ее скорости :

Рис. 7

Используя эти начальные условия и формулы (13) и (14), получаем шесть следующих уравнений для определения шести произвольных постоянных:

Если система уравнений (16) удовлетворяет условиям разрешимости, то из нее можно определить все шесть произвольных постоянных.

Начальные условия в форме (15) определяют единственное решение системы дифференциальных уравнений (9) при соблюдении соответствующих условий теории дифференциальных уравнений. Условия в других формах, как например, задание двух точек, через которые должна проходить траектория движущейся точки, могут дать или несколько решений, удовлетворяющих этих условиям, или не дать ни одного решения.

При движении точки в плоскости 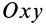имеется два дифференциальных уравнения движения. В решения этих уравнений входят четыре произвольные постоянные. Постоянные определяются из начальных условий

В случае прямолинейного движения точки имеется только одно дифференциальное уравнение и в его решение входят две произвольные постоянные. Для их определения необходимо задать начальные условия:

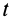
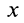
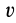
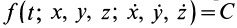
Задача интегрирования системы дифференциальных уравнений (9′) при заданных начальных условиях в общем случае является довольно трудной. Даже в простейшем случае прямолинейного движения, когда имеется только одно дифференциальное уравнение, его решение удается выразить точно в квадратурах лишь при определенной зависимости силы от времени , координаты и скорости . Поэтому важно определение таких соотношений из системы уравнений (9′), которые являются следствиями этой системы и в которые входят производные от координат точки только первого порядка. Такие соотношения, например, в виде называют первыми интегралами системы дифференциальных уравнений (9′).

Если из системы (9′) удается найти три независимых первых интеграла, то задача интегрирования упрощается, так как вместо интегрирования системы дифференциальных уравнений второго порядка достаточно проинтегрировать систему трех дифференциальных уравнений первого порядка, которую представляют эти первые интегралы.

В дальнейшем будет рассмотрен способ получения первых интегралов дифференциальных уравнений движения точки из так называемых общих теорем динамики в некоторых частных случаях движения точки.

Для выяснения особенностей решения второй основной задачи динамики, имеющей прикладное значение, рассмотрим ее решение для случая как прямолинейного, так и криволинейного движения материальной точки.

Две основные задачи динамики

Динамика имеет две основные задачи:

Прямая и обратная задачи динамики

В динамике изучают механическое движение в связи с силами, приложенными к движущимся объектам. Следовательно, перед динамикой стоят две основные задачи:

Наиболее просты с механической стороны эти задачи для одной материальной точки, хотя и здесь встречаются большие трудности математического характера.

(123)

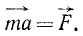
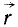
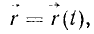
Если решают первую основную задачу динамики точки и движение точки определено в векторной форме, т. е. дан радиус-вектор как некоторая векторная функция времени t:

(54)

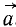
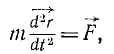
то надо определить по (57) ускорение , выражающееся второй производной от радиуса-вектора точки по времени t, и умножить его на массу т точки. Тогда мы получим следующее выражение основного закона динамики:

(125)

где правая часть даст нам искомую силу.
Если же решают вторую основную задачу динамики точки и задан вектор силы, но требуется определить радиус-вектор как функцию (54) от времени, то для решения задачи нужно интегрировать уравнение (125).

Значительно проще решать такие задачи не в векторной, а в координатной форме.

Все основные теоремы динамики точки могут быть выведены из трех дифференциальных уравнений движения материальной точки в прямоугольных координатах: mx = X; mу = Y; mz =Z

Дифференциальные уравнения движения точки в прямоугольных координатах

Пусть движение точки M задано в прямоугольных координатах кинематическими уравнениями

x = x (t), y = y (t), z = z (t). (58)

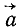
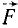
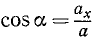
Преобразуем выражение (123) основного закона динамики; для этого определим проекции на оси координат ускорения и силы . Направляющие косинусы (67) ускорения являются вместе с тем и направляющими косинусами силы, так как направление ускорения совпадает с направлением силы. Умножая величины (123) на , получим: ma_x = F cos α.

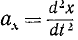
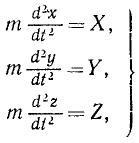
Но согласно (65) . Подставляем это значение и, пользуясь для проекции силы на ось абсцисс (и аналогично для проекций на оси у и z) знакомым нам по статике обозначением, получим

(126)

или, если обозначать вторые производные по времени двумя точками,

mx = X; mу = Y; mz =Z (126 / )

Система трех дифференциальных уравнений (126) второго порядка эквивалентна системе шести дифференциальных уравнений первого порядка:

(127)

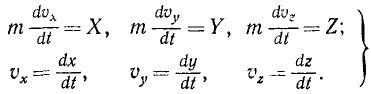
Уравнения (126) или (127) называют дифференциальными уравнениями движения материальной точки в прямоугольных координатах.

Из уравнений движения мы выведем все теоремы динамики. Они дают возможность решить и обе основные задачи динамики точки. В прямой задаче, когда кинематические уравнения движения (58) даны, решение сводится к дифференцированию этих уравнений: умножив на массу вторую производную от координаты но времени, получим проекцию силы. В обратной задаче, когда заданы проекции силы X, Y и Z, а нужно определить координаты точки х, у и z как функции времени (58), решение сводится к интегрированию трех совместных дифференциальных уравнений, где независимым переменным является время.

Три совместных дифференциальных уравнения (126) второго порядка определяют координаты х, у и z в функции времени t. Если движущаяся точка M совершенно свободна, то приложенные к ней силы могут быть функциями ее координат х, у и z, проекций ее скорости х, у и z и времени t:

Проинтегрировать их в общем виде невозможно, но при некоторых видах функции F эти интегралы могут быть получены. В очень многих случаях вычисления возможно проводить на интегрирующих машинах.

При интегрировании дифференциальных уравнений движения материальной точки появляется шесть постоянных интеграции, которые при решении каждой задачи должны быть определены из начальных условий

Постоянные интегрирования

Общие интегралы дифференциальных уравнений движения материальной точки содержат шесть постоянных интеграции: C₁, C₂, C_3, C₄, C₅, C₆. Эти постоянные величины отнюдь не являются произвольными, и в каждой частной задаче, при решении которой приходится интегрировать дифференциальные уравнения движения, постоянные интеграции должны быть определены из начальных условий. Если заданы положение и скорость движущейся точки для какого-либо мгновения t=t₀ (t₀ может быть равным или не равным нулю), то нужно определить постоянные C₁, C₂, C_3, C₄, C₅ и C₆ таким образом, чтобы при t=t₀ координаты х, у и z получили заданные значения х₀, у₀ и z₀ и производные
х, у и z — заданные значения υ_0x, υ_0y, и υ_0z.

Задача №1

Решение. Задача заключается в определении силы по заданному движению, т. е. является прямой задачей динамики. Условие выражено в физической системе единиц (СИ). При решении будем выражать длину в метрах, мaccy- в килограммах и время — в секундах.

Определим по (126) проекции силы на координатные оси, для чего сначала дважды продифференцируем заданные текущие координаты точек:

х=rk 2 cos kt, у =rk 2 sin kt, z=0

Умножая на т полученные значения проекций ускорения, определим в ньютонах проекции силы:

Направляющие косинусы силы найдем по (6):

Ответ. Сила постоянна по величине и перпендикулярна к оси Oz.

Задача №2

Дифференциальные уравнения движения снаряда напишем в виде (127):

Сокращаем на m, разделяем переменные:

откуда, интегрируя, находим:

Чтобы определить постоянные интеграции, подставим вместо t нуль, а вместо проекций скорости-их начальные значения υ_ox, υ_oy, и υ_oz, соответствующие мгновению t = 0. Получим

Теперь нетрудно определить и проекции начальной скорости:

Мы получили числовые значения постоянных интеграции:

Подставляя эти значения постоянных в уравнения и выражая проекции скоростей по (63), получим три новых дифференциальных уравнения:

Разделив переменные и проинтегрировав, получим

Для определения C₄, C₅ и C₆ подставим и в эти уравнения вместо t его частное значение 0, а вместо х, у и z —их частные значения x₀, у₀ и z₀:

При выбранной нами системе координат имеем x₀ =0; y_{0 =} 0; z₀ = + 30м, следовательно, C₄ = 0; C₅=0; C₆=+30.
Подставляя эти значения в уравнения, полученные после второго интегрирования, найдем кинематические уравнения движения снаряда:

Задача №3

Движение точки весом 2 Г выражается уравнениями x= 3cos2πt см; y=4sinπt см, где t выражено в секундах. Определить проекции силы, действующей на точку, в зависимости от ее координат.

Решение. Задача относится к прямым задачам динамики: по данному движению точки надо определить действующую силу. Для ее решения продифференцируем дважды кинематические уравнения движения точки и, умножив на m найденные х и у, получим X и Y.

Условие дано в технической системе единиц, и в этой задаче примем L в см, F в Г и T сек. Кинематические уравнения движения известны. Дифференцируя дважды, находим

х — 4π 2 3 cos 2πt = — 4π 2 x;
у = —4π 2 sin πt = — π 2 у.

Умножая массу 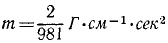на проекции ускорения, найдем проекции силы в граммах. Чтсбы перевести их в ньютоны, надо умножить число граммов на 0,00981.

Решим теперь эту же задачу в физической системе единиц. Принимать за основные единицы метр, килограмм и секунду в этой задаче нецелесообразно. Выразим L в см, M в г и T в сек.

В условии задачи дан вес точки G = 2 Г. Следовательно, ее масса m = 2 г. Умножая проекции ускорения на массу, выраженную в граммах, получим проекции силы в динах:

X = — 8π 2 x = — 78,88x [дин];
Y = — 2π 2 y = — 19,72y [дин].

Чтобы выразить их в ньютонах, надо число дин поделить на 100000.

Ответ. X =— 0,08χ Г = —78,88x дин = —0.0007888x н;
Y = —0,02x Г =— 19,72y дин = —0,0001972y н.

Обратим внимание на одно обстоятельство, которое легко усмотреть в только что решенной задаче. Определяя силу по заданному движению материальной точки, мы нашли, что движение произведено силой, являющейся функцией координат точки. Но мы могли бы выразить силу и как функцию времени. В самом деле, продифференцировав дважды кинематические уравнения движения и умножив вторые производные на m, найдем

X = — 12rnπ 2 cos 2πt; Y = —4rnπ 2 sin πt.

Так одно и то же движение может совершаться под действием различно выраженной силы.

Из этого же примера видно, что если точка движется в одной плоскости, то, приняв эту плоскость за плоскость хОу, можно описать движение точки системой первых двух дифференциальных уравнений движения (126′); третье же дифференциальное уравнение становится лишним.

Задача №4

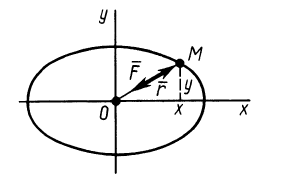
Найти плоскую траекторию точки M массы m, притягиваемой к неподвижному центру О с силой, пропорциональной расстоянию r и равной k 2 mr, при следующих начальных данных:

Решение. Задача относится к обратным задачам динамики: по заданной силе определить движение. Точка M описывает плоскую траекторию, и нам понадобятся только два уравнения движения.

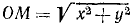
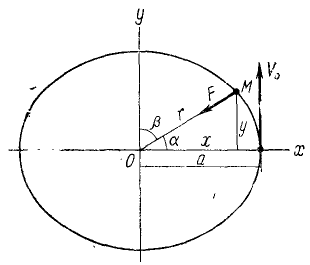
Если в какое-либо мгновение t точка M имела координаты х и у и находилась от центра на расстоянии (рис. 161), то проекции силы на оси координат:

Рис. 161

Дифференциальными уравнениями движения точки являются:

Сократим на т и умножим первое из уравнений на υ_xdt=dx, а второе—на υ_ydt = dy:

Интегрируем и умножаем на 2:

Для определения постоянных интеграции C₁ и C₂ подставляем в эти уравнения вместо переменных величин их начальные значения:

Значения постоянных вносим в уравнения, одновременно выражая υx и υy по (63):

Извлекаем квадратные корни, разделяем переменные н интегрируем:

Для определения постоянных интеграции C₃ и C₄ подставляем в эти уравнения вместо переменных величин t, х и у их начальные значения:

Эти значения постоянных интеграции вносим в уравнения:

Мы получили кинематические уравнения движения (58) точки в декартовых координатах. Чтобы определить траекторию, надо из них исключить время. Возводя в квадрат и складывая, получаем уравнение траектории

Ответ. Эллипс с полуосями a и .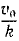

Перепишем это уравнение, сократив его на m:

Из этого уравнения видно, что падение не может быть равноускоренным, что по мере возрастания скорости сила сопротивления увеличивается, правая часть уравнения уменьшается и ускорение стремится к нулю.

Чтобы взять интеграл, перемножим соответственно левые и правые части этого уравнения и следующего выражения:

Это уравнение позволяет определить скорость падающего тела во всякое данное мгновение t. Оно уточняет известную формулу υ=gt, так как здесь учтено и сопротивление воздуха.

Ответ.

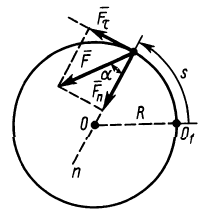
Движение точки можно описать в проекциях на оси естественного трехгранника двумя уравнениями:

Дифференциальные уравнения движения материальной точки в форме Эйлера. В кинематике мы изучали три способа определения движения точки: 1) векторный, 2) в прямоугольных координатах, 3) естественный. Соответственно и в динамике мы можем определить движение точки по заданным силам (или силы по заданному движению) векторным уравнением (125), в проекциях на прямоугольные оси — уравнениями (126), а также естественными уравнениями движения. Из многих форм уравнений движения эти три применяют наиболее часто.

Проецируя ускорение на оси естественного трехгранника, мы нашли (см. § 23), что проекции ускорения на касательную а_N, на главную нормаль αv и на бинормаль a_b выражаются следующими формулами:

и вместо трех составляющих полное ускорение имеет только две. Но сила всегда направлена по ускорению точки, а следовательно, проецируя силу на оси естественного трехгранника, мы и здесь получим только две составляющие (F_T — на касательную и F_N— на главную нормаль) и определим движение точки только двумя уравнениями:
(128)

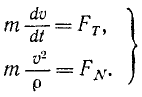
Задача №6

Горнолыжник в конце склона развил скорость 54 км/ч, после чего свободно скользил по горизонтальному прямолинейному участку пути. Определить длину и время свободного скольжения, если коэффициент трения лыж по снегу f’ = 0,051.

Сокращаем на m и разделяем переменные:

Чтобы определить постоянную C₁, подставим вместо t нуль, а вместо υ—начальное значение скорости —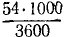= 15 м/сек:

Подставляя это значение C₁ в уравнение, полученное после интегрирования, и заменяя υ по (53), получим новое дифференциальное уравнение:

Разделим переменные и проинтегрируем:

В начальное мгновение лыжник не прошел еще никакого расстояния по горизонтальному участку, а потому C₂ = 0. Время скольжения до остановки определим, положив в уравнении, полученном для скорости,

Подставляя это значение t в последнее уравнение, найдем длину свободного скольжения.

Ответ. Время скольжения 30 сек, длина 225 м.

Задача №7

Маятник Борда для определения ускорения свободно падающих тел представляет собой латунный шарик массой 200 г, подвешенный на очень тонкой проволоке длиной 100 см. При качании шарик в наинизшем положении имеет скорость 8 см/сек. Определить натяжение проволоки в ее нижнем конце при наинизшем положении маятника.

Решение. В задаче применена физическая система единиц. Примем L в см, M в г, T в сек.

или, подставляя числовые значения,

откуда получаем ответ.
Ответ. T = 196 328 дин = 1,96328 н.

Движение точки в плоскости можно описать двумя уравнениями в полярных координатах.

Уравнения движения точки в полярных координатах

В ряде задач бывает удобно исследовать движение точки в полярных координатах. Примем без доказательства, что проекция ускорения точки на полярный радиус-вектор равна (r — rφ 2 ), а на перпендикулярное направление равна (rφ + 2rφ). Помножив на массу эти проекции ускорения точки и приравняв проекциям силы, напишем дифференциальные уравнения движения точки в полярных координатах:

(129)

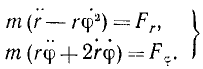
Далеко не всегда действующие силы бывают известны. Обычно остаются неизвестными внутренние силы. Для вывода некоторых общих теорем динамики и при решении некоторых частных задач бывает удобным выделить внутренние силы уже при написании дифференциальных уравнений движения.

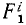
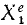
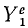
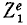
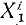
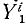
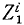
Рассмотрим сначала одну из материальных точек системы, например точку с индексом 1 , а сложив все внутренние, получим равнодействующую внутренних сил . Проекции этих сил обозначим ,, и ,, .

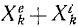
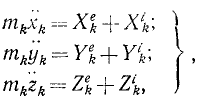
Аналогично поступим с силами, приложенными к остальным точкам, и заменим в написанных выше уравнениях проекции равнодействующей X_k суммой , то же сделаем по двум другим осям. Тогда дифференциальные уравнения примут вид:

(130)

Следовательно, движение свободной механической системы, состоящей из n материальных точек, определяется системой 3n дифференциальных уравнений второго порядка.

Если система не свободна, а на нее наложены связи, выражающие некоторую зависимость между координатами точек механической системы, то бывает возможным сократить число дифференциальных уравнений движения, о чем будет подробнее сказано в § 52 и § 53.

В ряде случаев оказывается целесообразным разделить все силы, действующие на материальные точки механической системы на две категории по иному признаку, а именно на активные силы и реакции связей. Как уже было сказано, реакции связей часто зависят от движения системы и не могут быть найдены, пока не определено движение системы. 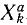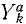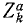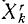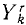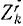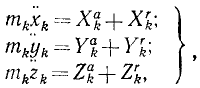Обозначая проекции равнодействующей всех активных сил, действующих на k-ю точку, , и , а проекции равнодействующей всех реакций связей, приложенных к k-й точке, , и , получим:

(130′)

Во всем вашем курсе (если это специально не оговорено) рассмотрены только свободные механические системы и механические системы с идеальными связями. Понятие идеальных связей нам уже встречалось в статике (см. § 4) и будет уточнено в динамике (см. § 51).

В дальнейшем из дифференциальных уравнений (130) и (130′) мы выведем общие теоремы динамики таких материальных систем.

Решение многих проблем по динамике механических систем сопряжено с большими трудностями математического характера. Интегрирующие машины в очень многих случаях дают возможность преодолеть эти трудности.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник