Две прямые пересечены секущей чему равна сумма внутренних односторонних углов если внутренние
Параллельность прямых
Определение параллельности прямых
Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.
Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.
Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.
Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.
На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.
Свойства и признаки параллельных прямых
Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.
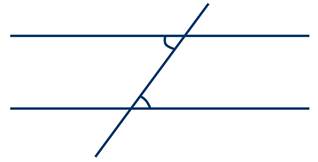
Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.
Если секущая проходит через две параллельные прямые, то:
∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.
∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.
Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.
А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.
Задача 1
Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.
Решение
Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.
Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.
Задача 2
Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.
Решение
Поскольку а II b, значит ∠MKD + ∠KDN = 180°.
Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.
Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.
Теорема о равенстве соответственных углов. Теорема о свойстве односторонних углов
Урок 18. Геометрия 7 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Теорема о равенстве соответственных углов. Теорема о свойстве односторонних углов»
Вспомним теорему о равенстве накрест лежащих углов:
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Если две параллельные прямые пересечены секущей, то соответственные углы равны.
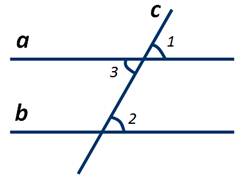
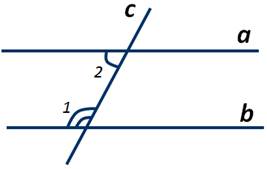
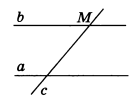
Пусть параллельные прямые а и b пересечены секущей c. Необходимо доказать, что соответственные углы 1 и 2 равны. Так как прямая а параллельна прямой b, то накрест лежащие углы 2 и 3 равны. ∠1 и ∠3 равны как вертикальные. Из равенств ∠2=∠3 и ∠1=∠3 следует, что ∠1=∠2. Теорема доказана.
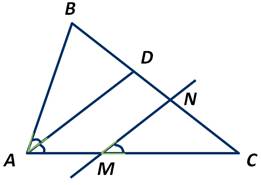
Пусть прямая MN параллельная биссектрисе AD треугольника АВС.
Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180 градусов.
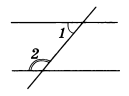
Пусть параллельные прямые а и b пересечены секущей c. Доказать, ∠1+∠2=180 градусов. Так как прямая а параллельна прямой b, то соответственные ∠1 и ∠3 равны. ∠2+∠3=180 градусов, так как углы 2 и 3 смежные. Тогда, из равенств угол ∠1=∠3 и ∠2+∠3=180 градусов, следует, что ∠1+∠2=180 градусов. Теорема доказана.
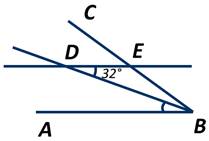
Например: пусть прямая DE параллельна стороне АВ треугольника АВС. Тогда ∠BAD+∠ADE=180 градусов.
Углы АВС и CED являются соответственными углами при параллельных прямых АВ и DE и секущей ВС, а значит, они равны. Следовательно, ∠CED=64 градуса.
Градусная мера одного из внутренних односторонних углов, образованных при пересечении двух параллельных прямых секущей, меньше градусной меры другого на 26 градусов. Вычислить градусные меры этих углов.
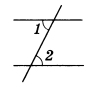
Пусть ∠1=x, тогда ∠2=x-26. Так как ∠1 и ∠2 являются внутренними односторонними при параллельных прямых а и b и секущей с, то их сумма равна 180 градусов, то есть ∠1+∠2=180 градусов.
Углы при пересечении двух прямых
Если какие-нибудь две прямые пересечены третьей прямой, то пересекающая их прямая называется секущей по отношению к прямым, которые она пересекает.
При пересечении двух прямых третьей, образуется два вида углов: внешние и внутренние.
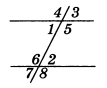
На рисунке изображены две прямые a и b, пересекаемые прямой c. Прямая c по отношению к прямым a и b является секущей. Синим цветом на рисунке обозначены внешние углы (∠1, ∠2, ∠7 и ∠8), а красным — внутренние углы (∠3, ∠4, ∠5 и ∠6).
Также при пересечении двух прямых третьей, образовавшиеся углы получают попарно следующие названия:
| Соответственные углы: ∠1 и ∠5, ∠3 и ∠7, ∠2 и ∠6, ∠4 и ∠8. |  |
| Внутренние накрест лежащие углы: ∠3 и ∠6, ∠4 и ∠5. |  |
| Внешние накрест лежащие углы: ∠1 и ∠8, ∠2 и ∠7. |  |
| Внутренние односторонние углы: ∠3 и ∠5, ∠4 и ∠6. |  |
| Внешние односторонние углы: ∠1 и ∠7, ∠2 и ∠8. |  |
Углы при пересечении параллельных прямых
Если секущая пересекает две параллельные прямые линии, то:
Внутренние односторонние углы
Еще один вид углов, образованных при пересечении двух прямых секущей — внутренние односторонние углы.
Две прямые разбивают плоскость на части. Та часть, которая лежит между прямыми — внутренняя. Углы, которые расположены в этой части, так и называются — внутренние. Внутренние односторонние углы — это углы, которые лежат внутри между прямыми по одну сторону от секущей (поэтому они так и называются).
При пересечении двух прямых секущей образуется две пары внутренних односторонних углов.

∠3 и ∠4
— внутренние односторонние углы при прямых a и b и секущей c.
Наибольший интерес вызывают внутренние накрест лежащие углы, образованные параллельными прямыми.
Свойство параллельных прямых
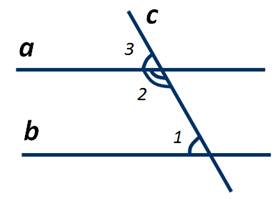
Если две параллельные прямые пересечены третьей прямой, то сумма внутренних односторонних углов равна 180º.

∠1 + ∠2 = 180º
(как внутренние односторонние при a ∥ b и секущей c).
Признак параллельных прямых
Если сумма внутренних односторонних углов равна 180º, то прямые параллельны.

А так как эти углы — внутренние односторонние при a и b и секущей c,
то a ∥ b (по признаку параллельных прямых).
Могут ли быть внутренние односторонние углы равны?
Да. Внутренние односторонние углы равны, если прямые параллельны, а секущая им перпендикулярна.

∠1 = ∠2
тогда и только тогда, когда a ∥ b, а секущая c перпендикулярна и прямой a, и прямой b.
Инструменты пользователя
Инструменты сайта
Боковая панель
Геометрия:
Контакты
Признаки параллельности двух прямых. Свойства параллельных прямых
Признаки параллельности двух прямых
Теорема 1. Если при пересечении двух прямых секущей:
прямые параллельны (рис.1).
Доказательство. Ограничимся доказательством случая 1.
Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны. Например, ∠ 4 = ∠ 6. Докажем, что а || b.
Предположим, что прямые а и b не параллельны. Тогда они пересекаются в некоторой точке М и, следовательно, один из углов 4 или 6 будет внешним углом треугольника АВМ. Пусть для определенности ∠ 4 — внешний угол треугольника АВМ, а ∠ 6 — внутренний. Из теоремы о внешнем угле треугольника следует, что ∠ 4 больше ∠ 6, а это противоречит условию, значит, прямые а и 6 не могут пересекаться, поэтому они параллельны.
Замечание. Способ, которым мы только что доказали случай 1 теоремы 1, называется методом доказательства от противного или приведением к нелепости. Первое название этот способ получил потому, что в начале рассуждения делается предположение, противное (противоположное) тому, что требуется доказать. Приведением к нелепости он называется вследствие того, что, рассуждая на основании сделанного предположения, мы приходим к нелепому выводу (к абсурду). Получение такого вывода заставляет нас отвергнуть сделанное вначале допущение и принять то, которое требовалось доказать.
Задача 1. Построить прямую, проходящую через данную точку М и параллельную данной прямой а, не проходящей через точку М.
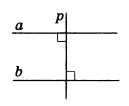
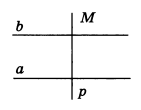
Решение. Проводим через точку М прямую р перпендикулярно прямой а (рис. 3).
Затем проводим через точку М прямую b перпендикулярно прямой р. Прямая b параллельна прямой а согласно следствию из теоремы 1.
Из рассмотренной задачи следует важный вывод:
через точку, не лежащую на данной прямой, всегда можно провести прямую, параллельную данной.
Основное свойство параллельных прямых состоит в следующем.
Аксиома параллельных прямых. Через данную точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Рассмотрим некоторые свойства параллельных прямых, которые следуют из этой аксиомы.
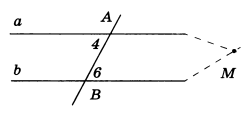
1) Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую (рис.4).
2) Если две различные прямые параллельны третьей прямой, то они параллельны (рис.5).
Справедлива и следующая теорема.
Теорема 2. Если две параллельные прямые пересечены секущей, то:
Следствие 2. Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой (см. рис.2).
Замечание. Теорема 2 называется обратной теореме 1. Заключение теоремы 1 является условием теоремы 2. А условие теоремы 1 является заключением теоремы 2. Не всякая теорема имеет обратную, т. е. если данная теорема верна, то обратная теорема может быть неверна.
Поясним это на примере теоремы о вертикальных углах. Эту теорему можно сформулировать так: если два угла вертикальные, то они равны. Обратная ей теорема была бы такой: если два угла равны, то они вертикальные. А это, конечно, неверно. Два равных угла вовсе не обязаны быть вертикальными.
Пример 1. Две параллельные прямые пересечены третьей. Известно, что разность двух внутренних односторонних углов равна 30°. Найти эти углы.
Решение. Пусть условию отвечает рисунок 6.
Углы 1 и 2 внутренние односторонние, их сумма равна 180°, т. е.
∠ l + ∠ 2 = 180°. (1)
Подставим в равенство (1) значения углов 1 и 2, получим
х + 30° + х = 180°.
Пример 2. Две параллельные прямые пересечены третьей. Известно, что сумма двух внутренних накрест лежащих углов равна 150°. Чему равны эти углы и остальные шесть?
Решение. Пусть условию задачи соответствует рисунок 7.
Углы 1 и 2 внутренние накрест лежащие, следовательно, они равны. Сумма этих углов по условию задачи равна 150°, тогда ∠ 1 = ∠ 2 = 75°.
Найдем остальные углы (рис. 8):
Получили четыре угла по 75°, четыре угла по 105°.