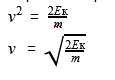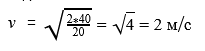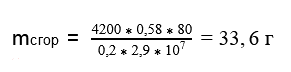Е большая в физике это что
Экспонента и число е: просто и понятно.
Число e всегда волновало меня — не как буква, а как математическая константа. Что число е означает на самом деле?
Разные математические книги и даже моя горячо любимая Википедия описывает эту величественную константу совершенно бестолковым научным жаргоном:
Математическая константа е является основанием натурального логарифма.
Если заинтересуетесь, что такое натуральный логарифм, найдете такое определение:
Натуральный логарифм, ранее известный как гиперболический логарифм, является логарифмом с основанием е, где е – иррациональная константа, приблизительно равная 2.718281828459.
Определения, конечно, правильные. Но понять их крайне сложно. Конечно, Википедия в этом не виновата: обычно математические пояснения сухи и формальны, составляются по всей строгости науки. Из-за этого новичкам сложно осваивать предмет (а когда-то каждый был новичком).
С меня хватит! Сегодня я делюсь своими высокоинтеллектуальными соображениями о том, что такое число е, и чем оно так круто! Отложите свои толстые, наводящие страх математические книжки в сторону!
Число е – это не просто число
Описывать е как «константу, приблизительно равную 2,71828…» — это все равно, что называть число пи «иррациональным числом, приблизительно равным 3,1415…». Несомненно, так и есть, но суть по-прежнему ускользает от нас.
Число пи — это соотношение длины окружности к диаметру, одинаковое для всех окружностей. Это фундаментальная пропорция, свойственная всем окружностям, а следовательно, она участвует в вычислении длины окружности, площади, объема и площади поверхности для кругов, сфер, цилиндров и т.д. Пи показывает, что все окружности связаны, не говоря уже о тригонометрических функциях, выводимых из окружностей (синус, косинус, тангенс).
Число е является базовым соотношением роста для всех непрерывно растущих процессов. Число е позволяет взять простой темп прироста (где разница видна только в конце года) и вычислить составляющие этого показателя, нормальный рост, при котором с каждой наносекундой (или даже быстрее) всё вырастает еще на немного.
Число е участвует как в системах с экспоненциальным, так и постоянным ростом: население, радиоактивный распад, подсчет процентов, и много-много других. Даже ступенчатые системы, которые не растут равномерно, можно аппроксимировать с помощью числа е.
Также, как любое число можно рассматривать в виде «масштабированной» версии 1 (базовой единицы), любую окружность можно рассматривать в виде «масштабированной» версии единичной окружности (с радиусом 1). И любой коэффициент роста может быть рассмотрен в виде «масштабированной» версии е («единичного» коэффициента роста).
Так что число е – это не случайное, взятое наугад число. Число е воплощает в себе идею, что все непрерывно растущие системы являются масштабированными версиями одного и того же показателя.
Понятие экспоненциального роста
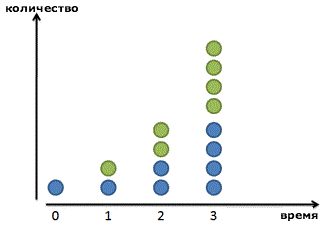
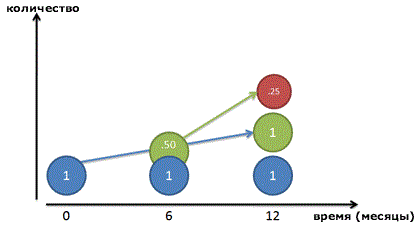
Давайте начнем с рассмотрения базовой системы, которая удваивается за определенный период времени. Например:
И выглядит это примерно так:
Деление на два или удваивание – это очень простая прогрессия. Конечно, мы можем утроить или учетверить, но удваивание более удобно для пояснения.
Математически, если у нас есть х разделений, мы получаем в 2^x раз больше добра, чем было вначале. Если сделано только 1 разбиение, получаем в 2^1 раза больше. Если разбиений 4, у нас получится 2^4=16 частей. Общая формула выглядит так:
Другими словами, удвоение – это 100% рост. Мы можем переписать эту формулу так:
Это то же равенство, мы только разделили «2» на составные части, которыми в сущности и является это число: начальное значение (1) плюс 100%. Умно, да?
Конечно, мы можем подставить и любое другое число (50%, 25%, 200%) вместо 100% и получить формулу роста для этого нового коэффициента. Общая формула для х периодов временного ряда будет иметь вид:
Это просто означает, что мы используем норму возврата, (1 + прирост), «х» раз подряд.
Наша формула предполагает, что прирост происходит дискретными шагами. Наши бактерии ждут, ждут, а потом бац!, и в последнюю минуту они удваиваются в количестве. Наша прибыль по процентам от депозита магическим образом появляется ровно через 1 год. На основе формулы, написанной выше, прибыль растет ступенчато. Зеленые точки появляются внезапно.
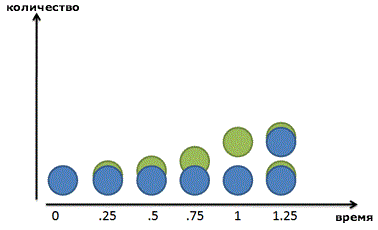
Но мир не всегда таков. Если мы увеличим картинку, мы увидим, что наши друзья-бактерии делятся постоянно:
Зеленый малый не возникает из ничего: он медленно вырастает из синего родителя. После 1 периода времени (24 часа в нашем случае), зеленый друг уже полностью созрел. Повзрослев, он стает полноценным синим членом стада и может создавать новые зеленые клеточки сам.
Эта информация как-то изменит наше уравнение?
Не-а. В случае с бактериями, полусформированные зеленые клетки все же не могут ничего делать, пока не вырастут и совсем не отделятся от своих синих родителей. Так что уравнение справедливо.
Но деньги меняют все
С деньгами дела обстоят по-другому. Как только мы зарабатываем пару монет прибыли, эти монетки начинают приносить свои микро-прибыли. Нет необходимости ждать, пока набежит целый рубль — свежим денежкам совсем не нужно дозревать, чтобы начать плодоносить.
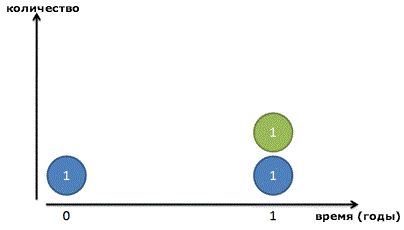
Основываясь на нашей старой формуле, прирост процента выглядит примерно так:
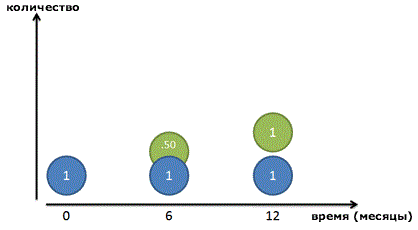
Но опять же, это не совсем правильно: вся сумма процента появляется в последний день. Давайте посмотрим поближе и разделим год на два промежутка. Мы зарабатываем 100% прибыль каждый год, или по 50% каждые 6 месяцев. Таким образом, мы заработаем 50 копеек в первые полгода, и другие 50 копеек во вторую половину года:
И все равно, это неверно! Конечно, наш рубль-родитель (Синий кружок) зарабатывает рубль в течение года. Но после 6 месяцев мы получим 50-копеечный кусочек прибыли – готовые деньги, которыми мы пренебрегаем! Эти 50 копеек уже могли бы зарабатывать свои собственные деньги:
Поскольку наш коэффициент равен 50% каждые полгода, эти 50 копеек могли бы заработать еще 25 копеек (50% от 50 копеек). В конце года мы бы получили:
Если все сложить, получится 2,25 рублей. Мы заработали 1,25 рубля всего на одном исходном рубле, и это даже лучше, чем удвоение!
Вернемся к формуле. Рост за два полу-периода по 50% составит:
Переходим на составной рост
Идем дальше. Давайте поделим рост не на два периода по 50%, а на 3 сегмента по 33% каждый. Кто сказал, что надо ждать целых 6 месяцев до начала получения прибыли? Давайте детализируем наши вычисления.
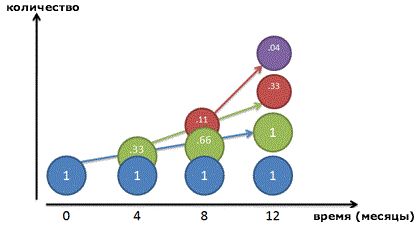
Вот так выглядит наш рост, расписанный на 3 составных периода:
Фуух! Спустя 12 месяцев у нас получается: 1 + 1 + 0.33 + 0.04 или примерно 2.37 рубля.
Потратим еще чуть времени, чтобы понять, что на самом деле происходит с таким ростом:
Теперь понятнее? Поначалу это сложно — я и сам запутался, пока рисовал все эти графики. Главное понять, что каждый «рубль» создает маленьких помощников, а те, в свою очередь, создают помощников себе, и так далее.
Если рассматривать год как 3 равных периода, формула роста будет такой:
рост = (1 + 100%/3) 3 = 2.37037.
Мы заработали 1.37 рубля, а это даже лучше, чем те 1.25, что получились у нас в предыдущий раз!
Можно ли преумножать деньги бесконечно?
А почему бы не разбить год на более короткие периоды? Как насчет месяца, дня, часа или даже наносекунды? Наша прибыль взлетит до небес?
Прибыль увеличится, но уже не намного. Попробуем подставить в нашу волшебную формулу разные значения n, и получим следующее:
Диэлектрическая проницаемость и электрическая постоянная
Электрическая постоянная — характеристика вакуума, она описывает его электрические свойства. А диэлектрическая проницаемость описывает свойства веществ – диэлектриков, ослабляющих взаимодействие зарядов.
Электрическая постоянная
Обозначают ее \(\large \varepsilon_<0>\), она описывает электрические свойства вакуума и является одной из фундаментальных физических постоянных.
Значение электрической постоянной равно:
Совместно с магнитной постоянной (ссылка) \(\large \mu_<0>\) определяет скорость, с которой в вакууме распространяются электромагнитные волны (например, видимый свет).
В формуле закона Кулона присутствует константа «k». Число «k» вычисляют по формуле, которая связывает его с постоянной \(\large \varepsilon_<0>\) так:
Так же, эта константа встречается в формуле, описывающей напряженность электрического поля.
Диэлектрическая проницаемость вещества
Некоторые вещества могут ослаблять взаимодействие зарядов.
Вещества, ослабляющие взаимодействие заряженных частиц, называют изолирующими веществами, или диэлектриками.
Для пояснения рассмотрим электрические свойства дистиллированной воды.
Расположим в вакууме два положительных заряда на некотором расстоянии один от другого, они будут отталкиваться Кулоновскими силами.
Затем, не меняя заряды и расстояние между ними, переместим их в дистиллированную воду. Мы обнаружим, что в воде они будут отталкиваться слабее в 81 раз (рис. 1).
В нижней части рисунка силы отталкивания зарядов в воде обозначены короткими синими векторами. Длина этих векторов должна быть в 81 раз меньше, чем длина векторов сил в вакууме в верхней части рисунка. Однако, векторы имеют большую длину на рисунке, чем в реальности, так как, если их уменьшить в нужное число раз, то их невозможно будет рассмотреть.
Диэлектрическая проницаемость \(\large \varepsilon\) описывает изолирующие свойства диэлектриков. Она показывает, во сколько раз внутри вещества — диэлектрика ослабляется взаимодействие зарядов.
Ослабление взаимодействия происходит за счет ослабления напряженности электростатического поля в диэлектрике.
Диэлектрическая проницаемость некоторых веществ
Вы можете использовать данные таблички для решения большинства школьных задач физики.
Для некоторых веществ значения проницаемости округлены. К примеру, существуют стекла, имеющие значение проницаемости 6,0, и в то же время, проницаемость некоторых стекол может достигать значения 10,0. А в таблице для стекла указано среднее значение 8,0.
Чтобы осуществить более серьезные расчеты, не относящиеся к учебным, пожалуйста, воспользуйтесь специализированными справочниками.
ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ
Полезное
Смотреть что такое «ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ» в других словарях:
электрическая постоянная — Коэффициент, применяемый при записи ряда соотношений в СИ, равный величине, обратной произведению магнитной постоянной на квадрат скорости света в пустоте. Примечание — Электрическая постоянная приблизительно равна 8,85419 • 10 12 Ф/м … Справочник технического переводчика
ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ — (см.) … Большая политехническая энциклопедия
электрическая постоянная — электрическая постоянная; отрасл. диэлектрическая проницаемость пустоты Скалярная величина, характеризующая электрическое поле в пустоте, равная отношению суммарного электрического заряда, заключенного внутри некоторой замкнутой поверхности, к… … Политехнический терминологический толковый словарь
Электрическая постоянная — (ранее также носила название диэлектрической постоянной) физическая константа, скалярная величина, определяющая напряжённость электрического поля в вакууме; входящая в выражения некоторых законов электромагнетизма, в том числе закона Кулона … Википедия
электрическая постоянная — elektrinė konstanta statusas T sritis automatika atitikmenys: angl. electric constant; permittivity constant; permittivity of free space; permittivity of vacuum vok. dielektrische konstante, f; Dielektrizitätskonstante, f; elektrische… … Automatikos terminų žodynas
электрическая постоянная — elektrinė konstanta statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. electric constant; permittivity of vacuum vok. absolute Dielektrizitätskonstante, f;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
электрическая постоянная — elektrinė konstanta statusas T sritis fizika atitikmenys: angl. permittivity constant; permittivity of free space; permittivity of vacuum vok. Dielektrizitätskonstante, f; elektrische Feldkonstante, f; Verschiebungskonstante, f rus. абсолютная… … Fizikos terminų žodynas
Мощность
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение мощности
Допустим, нам необходимо убрать урожай пшеницы с поля площадью 100 га. Это можно сделать вручную или с помощью комбайна. Очевидно, что пока человек обработает 1 га площади, комбайн успеет сделать намного больше. В данном случае разница между человеком и техникой — именно то, что называют мощностью. Отсюда вытекает первое определение.
Мощность в физике — это количество работы, которая совершается за единицу времени.
Рассмотрим другой пример: между точкой А и точкой Б расстояние 15 км, которое человек проходит за 3 часа, а автомобиль может проехать всего за 10 минут. Понятно, что одно и то же количество работы они сделают за разное время. Что показывает мощность в данном случае? Как быстро или с какой скоростью выполняется некая работа.
В электромеханике данная величина тоже связана со скоростью, а конкретно — с тем, как быстро передается ток по участку цепи. Исходя из этого, мы можем рассмотреть еще одно определение.
Мощность — это скалярная физическая величина, которая характеризует скорость передачи энергии от системы к системе или скорость преобразования, изменения, потребления энергии.
Напомним, что скалярными величинами называются те, значение которых выражается только числом (без вектора направления).
Мощность человека в зависимости от деятельности
Вид деятельности
Мощность, Вт
Бег со скоростью 9 км/ч
Плавание со скоростью 50 м/мин
Как обозначается мощность: единицы измерения
В таблице выше вы увидели обозначение в ваттах, и читая инструкции к бытовой технике, можно заметить, что среди характеристик прибора обязательно указано количество ватт. Это единица измерения механической мощности, используемая в международной системе СИ. Она обозначается буквой W или Вт.
Измерение мощности в ваттах было принято в честь шотландского ученого Джеймса Уатта — изобретателя паровой машины. Он стал одним из родоначальников английской промышленной революции.
В физике принято следующее обозначение мощности: 1 Вт = 1 Дж / 1с.
Это значит, что за 1 ватт принята мощность, необходимая для совершения работы в 1 джоуль за 1 секунду.
В каких единицах еще измеряется мощность? Ученые-астрофизики измеряют ее в эргах в секунду (эрг/сек), а в автомобилестроении до сих пор можно услышать о лошадиных силах.
Интересно, что автором этой последней единицы измерения стал все тот же шотландец Джеймс Уатт. На одной из пивоварен, где он проводил свои исследования, хозяин накачивал воду для производства с помощью лошадей. И Уатт выяснил, что 1 лошадь за секунду поднимает около 75 кг воды на высоту 1 метр. Вот так и появилось измерение в лошадиных силах. Правда, сегодня такое обозначение мощности в физике считается устаревшим.
Одна лошадиная сила — это мощность, необходимая для поднятия груза в 75 кг за 1 секунду на 1 метр. 🐴
Закон сохранения механической энергии
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Энергия: что это такое
Если мы погуглим определение слова «Энергия», то скорее всего найдем что-то про формы взаимодействия материи. Это верно, но совершенно непонятно.
Поэтому давайте условимся здесь и сейчас, что энергия — это запас, который пойдет на совершение работы.
Энергия бывает разных видов: механическая, электрическая, внутренняя, гравитационная и так далее. Измеряется она в Джоулях (Дж) и чаще всего обозначается буквой E.
Механическая энергия
Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу.
Она представляет собой совокупность кинетической и потенциальной энергии. Кинетическая энергия — это энергия действия. Потенциальная — ожидания действия.
Представьте, что вы взяли в руки канцелярскую резинку, растянули ее и отпустили. Из растянутого положения резинка просто «полетит», как только вы ей позволите это сделать. В этом процессе в момент натяжения резинка обладает потенциальной энергией, а в момент полета — кинетической.
Еще один примерчик: лыжник скатывается с горы. В самом начале — на вершине — у него максимальная потенциальная энергия, потому что он в режиме ожидания действия (ждущий режим 😂), а внизу горы он уже явно двигается, а не ждет, когда с ним это случится — получается, внизу горы кинетическая энергия.
Кинетическая энергия
Еще разок: кинетическая энергия — это энергия действия. Величина, которая очевиднее всего характеризует действие — это скорость. Соответственно, в формуле кинетической энергии точно должна присутствовать скорость.
Кинетическая энергия
Ек = (m*v^2)/2
Ек — кинетическая энергия [Дж]
Чем быстрее движется тело, тем больше его кинетическая энергия. И наоборот — чем медленнее, тем меньше кинетическая энергия.
Задачка раз
Определить кинетическую энергию собаченьки массой 10 килограмм, если она бежала за мячом с постоянной скоростью 2 м/с.
Решение:
Формула кинетической энергии Ек = (m*v^2)/2
Ответ: кинетическая энергия пёсы равна 20 Дж.
Задачка два
Найти скорость бегущего по опушке гнома, если его масса равна 20 килограммам, а его кинетическая энергия — 40 Дж
Решение:
Формула кинетической энергии Ек = (m*v^2)/2
Ответ: гном бежал со скоростью 2 м/с.
Потенциальная энергия
В отличие от кинетической энергии, потенциальная чаще всего тем меньше, чем скорость больше. Потенциальная энергия — это энергия ожидания действия.
Например, потенциальная энергия у сжатой пружины будет очень велика, потому что такая конструкция может привести к действию, а следовательно — к увеличению кинетической энергии. То же самое происходит, если тело поднять на высоту. Чем выше мы поднимаем тело, тем больше его потенциальная энергия.
Потенциальная энергия деформированной пружины
Еп — потенциальная энергия [Дж]
x — удлинение пружины [м]
Потенциальная энергия
Еп = mgh
Еп — потенциальная энергия [Дж]
g — ускорение свободного падения [м/с^2]
На планете Земля g ≃ 9,8 м/с^2
Задачка раз
Найти потенциальную энергию рака массой 0,1 кг, который свистит на горе высотой 2500 метров. Ускорение свободного падения считать равным 9,8 м/с^2.
Решение:
Формула потенциальной энергии Еп = mgh
Eп = 0,1 * 9,8 * 2500=2450 Дж
Ответ: потенциальная энергия рака, свистящего на горе, равна 2450 Дж.
Задачка два
Найти высоту горки, с которой собирается скатиться лыжник массой 65 килограмм, если его потенциальная энергия равна 637 кДж. Ускорение свободного падения считать равным 9,8 м/с^2.
Решение:
Формула потенциальной энергии Еп = mgh
Переведем 637 кДж в Джоули.
637 кДж = 637000 Дж
h = 637 000/(65 * 9,8) = 1000 м
Ответ: высота горы равна 1000 метров.
Задачка три
Два шара разной массы подняты на разную высоту относительно поверхности стола (см. рисунок). Сравните значения потенциальной энергии шаров E1 и E2. Считать, что потенциальная энергия отсчитывается от уровня крышки стола.
Решение:
Потенциальная энергия вычисляется по формуле: E = mgh
Таким образом, получим, что
Ответ: E1 = E2.
Закон сохранения энергии
В физике и правда ничего не исчезает бесследно. Чтобы это как-то выразить, используют законы сохранения. В случае с энергией — Закон сохранения энергии.
Закон сохранения энергии
Полная механическая энергия замкнутой системы остается постоянной.
Полная механическая энергия — это сумма кинетической и потенциальной энергий. Математически этот закон описывается так:
Закон сохранения энергии
Еполн.мех. = Еп + Eк = const
Еполн.мех. — полная механическая энергия системы [Дж]
Еп — потенциальная энергия [Дж]
Ек — кинетическая энергия [Дж]
const — постоянная величина
Задачка раз
Мяч бросают вертикально вверх с поверхности Земли. Сопротивление воздуха пренебрежимо мало. Как изменится высота подъёма мяча при увеличении начальной скорости мяча в 2 раза?
Решение:
Должен выполняться закон сохранения энергии:
В начальный момент времени высота равна нулю, значит Еп = 0. В этот же момент времени Ек максимальна.
В конечный момент времени все наоборот — кинетическая энергия равна нулю, так как мяч уже не может лететь выше, а вот потенциальная максимальна, так как мяч докинули до максимальной высоты.
Это можно описать соотношением:
Еп1 + Ек1 = Еп2 + Ек2
Разделим на массу левую и правую часть
Из соотношения видно, что высота прямо пропорциональна квадрату начальной скорости, значит при увеличении начальной скорости мяча в два раза, высота должна увеличиться в 4 раза.
Ответ: высота увеличится в 4 раза
Задачка два
Тело массой m, брошенное с поверхности земли вертикально вверх с начальной скоростью v0, поднялось на максимальную высоту h0. Сопротивление воздуха пренебрежимо мало. Чему будет равна полная механическая энергия тела на некоторой промежуточной высоте h?
Решение
По закону сохранения энергии полная механическая энергия изолированной системы остаётся постоянной. В максимальной точке подъёма скорость тела равна нулю, а значит, оно будет обладать исключительно потенциальной энергией Емех = Еп = mgh0.
Таким образом, на некоторой промежуточной высоте h, тело будет обладать и кинетической и потенциальной энергией, но их сумма будет иметь значение Емех = mgh0.
Ответ: Емех = mgh0.
Задачка три
Мяч массой 100 г бросили вертикально вверх с поверхности земли с начальной скоростью 6 м/с. На какой высоте относительно земли мяч имел скорость 2 м/с? Сопротивлением воздуха пренебречь.
Решение:
Переведем массу из граммов в килограммы:
У поверхности земли полная механическая энергия мяча равна его кинетической энергии:
Е = Ек0 = (m*v^2)/2 = (0,1*6^2)/2 = 1,8 Дж
На высоте h потенциальная энергия мяча есть разность полной механической энергии и кинетической энергии:
mgh = E — (m*v^2)/2 = 1,8 — (0,1 * 2^2)/2 = 1,6 Дж
h = E/mg = 1,6/0,1*10 = 1,6 м
Ответ: мяч имел скорость 2 м/с на высоте 1,6 м
Переход механической энергии во внутреннюю
Внутренняя энергия — это сумма кинетической энергии хаотичного теплового движения молекул и потенциальной энергии их взаимодействия. То есть та энергия, которая запасена у тела за счет его собственных параметров.
Часто механическая энергия переходит во внутреннюю. Происходит этот процесс путем совершения механической работы над телом. Например, если сгибать и разгибать проволоку — она будет нагреваться.
Или если кинуть мяч в стену, часть энергии при ударе перейдет во внутреннюю.
Задачка
Какая часть начальной кинетической энергии мяча при ударе о стену перейдет во внутреннюю, если полная механическая энергия вначале в два раза больше, чем в конце?
Решение:
В самом начале у мяча есть только кинетическая энергия, то есть Емех = Ек.
В конце механическая энергия равна половине начальной, то есть Емех/2 = Ек/2
Часть энергии уходит во внутреннюю, значит Еполн = Емех/2 + Евнутр
Емех = Емех/2 + Евнутр
Ответ: во внутреннюю перейдет половина начальной кинетической энергии
Закон сохранения энергии в тепловых процессах
Чтобы закон сохранения энергии для тепловых процессов был сформулирован, было сделано два важных шага. Сначала французский математик и физик Жан Батист Фурье установил один из основных законов теплопроводности. А потом Сади Карно определил, что тепловую энергию можно превратить в механическую.
Вот что сформулировал Фурье:
При переходе теплоты от более горячего тела к более холодному температуры тел постепенно выравниваются и становятся едиными для обоих тел — наступает состояние термодинамического равновесия.
Таким образом, первым важным открытием было открытие того факта, что все протекающие без участия внешних сил тепловые процессы необратимы.
Дальше Карно установил, что тепловую энергию, которой обладает нагретое тело, непосредственно невозможно превратить в механическую энергию для производства работы. Это можно сделать, только если часть тепловой энергии тела с большей температурой передать другому телу с меньшей температурой и, следовательно, нагреть его до более высокой температуры.
Закон сохранения энергии в тепловых процессах
При теплообмене двух или нескольких тел абсолютное количество теплоты, которое отдано более нагретым телом, равно количеству теплоты, которое получено менее нагретым телом.
Математически его можно описать так:
Уравнение теплового баланса
Q отд = Q пол
Qотд — отданное системой количество теплоты [Дж]
Q пол — полученное системой количество теплоты [Дж]
Данное равенство называется уравнением теплового баланса. В реальных опытах обычно получается, что отданное более нагретым телом количество теплоты больше количества теплоты, полученного менее нагретым телом:
Это объясняется тем, что некоторое количество теплоты при теплообмене передаётся окружающему воздуху, а ещё часть — сосуду, в котором происходит теплообмен.
Задачка раз
Сколько граммов спирта нужно сжечь в спиртовке, чтобы нагреть на ней воду массой 580 г на 80 °С, если учесть, что на нагревание пошло 20% затраченной энергии.
Удельная теплота сгорания спирта 2,9·10^7Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг·°С).
Решение:
При нагревании тело получает количество теплоты
где c — удельная теплоемкость вещества
При сгорании тела выделяется энергия
где q — удельная теплота сгорания топлива
По условию задачи нам известно, что на нагревание пошло 20% затраченной энергии.
Ответ: масса сгоревшего топливаа равна 33,6 г.
Задачка два
Какое минимальное количество теплоты необходимо для превращения в воду 500 г льда, взятого при температуре −10 °С? Потерями энергии на нагревание окружающего воздуха пренебречь. Удельная теплоемкость льда равна 2100 Дж/кг*℃, удельная теплота плавления льда равна 3,3*10^5 Дж/кг.
Решение:
Для нагревания льда до температуры плавления необходимо:
Qнагрев = 2100 * 0,5 * (10-0) = 10500 Дж
Для превращения льда в воду:
Qпл = 3,3 * 10^5 * 0,5 = 165000 Дж
Q = Qнагрев + Qпл = 10500 + 165000 = 175500 Дж = 175,5 кДж
Ответ: чтобы превратить 0,5 кг льда в воду при заданных условиях необходимо 175,5 кДж тепла.