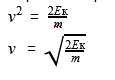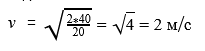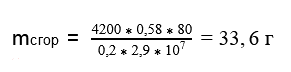E mv2 2 что за формула
Формула кинетической энергии в физике
Одним из важнейших понятий в физике является энергия, то есть способность тела совершать ту или иную работу. Механическая энергия подразделяется на кинетическую и потенциальную. Рассмотрим первый ее вид.
Кинетическая энергия – понятие и определение
Кинетическая энергия – это способность движущегося тела совершать определенную работу.
Например, движущийся автомобиль способен снести находящееся перед ним препятствие, а падающий камень – оставить вмятину на металлической пластинке.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Кинетическая энергия зависит от скорости движения и массы тела. Она описывается формулой:
Единицей измерения кинетической энергии является Джоуль (Дж).
Проведя простые преобразования, легко вывести формулы для вычисления массы тела и скорости движения:
Из основной формулы видно: во сколько раз изменяется масса тела, во столько раз изменяется и величина кинетической энергии. Например, если масса будет уменьшена или увеличена в 5 раз, то и величина кинетической энергии станет соответственно меньше или больше в 5 раз.
При увеличении скорости кинетическая энергия увеличивается в квадратичной зависимости. Допустим, скорость движения тела стала в 6 раз больше. Соответственно его кинетическая энергия возросла в 36 раз.
Формула кинетической энергии тела справедлива только для скоростей значительно меньших, чем скорость света. Если же скорость движения приближается к 300 000 км/с, то тут начинает действовать теория относительности, созданная Альбертом Эйнштейном.
Кинетическая энергия зависит от особенностей рассмотрения системы. Если тело принимают как макроскопический объект, то оно будет обладать внутренней энергией. В этом случае кинетическая энергия возникнет только в момент его движения.
Это же тело можно рассматривать и с микроскопической точки зрения. Тепловое движение атомов и молекул обуславливает внутреннюю энергию тела. В то же время средняя кинетическая энергия этого движения пропорциональна абсолютной температуре тела. Коэффициент этой пропорциональной зависимости называется постоянной Больцмана.
Кинетическая энергия атомов и молекул при рассмотрении тела на микроскопическом уровне описывается формулой:
\(E_k=\frac32kT\)
где \(k\) – это постоянная Больцмана.
Теорема об изменении кинетической энергии
Рассмотрим наиболее простой пример движения, при котором скорость движения и сила, действующая на тело имеют одинаковое направление. Тело совершает перемещение (S), так как сила (F) совершает работу (A). Также она изменяет и скорость движения, придавая телу некоторое ускорение. Это свидетельствует о наличии связи между работой силы и изменением скорости движения.
В данном случае работа силы будет описываться формулой:
Запишем второй закон Ньютона в стандартном виде:
При условии, что движение является равноускоренным (сила не зависит от координат и времени), работу можно записать так:
Вспомним формулу из курса кинематики, связывающую перемещение, ускорение, начальную и конечную скорости движения тела:
Подставляем ее в формулу работы:
Полученное равенство показывает, что разность между кинетической энергией в конечной и начальный момент времени равна работе силы. Это позволяет сформулировать теорему об изменении кинетической энергии.
Изменение кинетической энергии тела равна равнодействующей всех сил или работе силы:
Таким образом, сила будет совершать отрицательную работу, если она направлена в сторону, противоположную движению тела. В этом случае начальная кинетическая энергия будет больше, чем конечная:
Так как сила имеет противоположное скорости направление, то модуль скорости будет уменьшаться, что и становится причиной уменьшения величины кинетической энергии.
Если же сила будет направлена в сторону движения, то кинетическая энергия будет возрастать:
Фактически теорему об изменении кинетической энергии можно рассматривать как иную формулировку второго закона Ньютона. Поэтому ее использование возможно в различных случаях, например, при рассмотрении действия силы трения, тяжести или упругости.
Примеры решения задач, как найти кинетическую энергию
Рассмотрим примеры решения задач на нахождение кинетической энергии.
Задача 1
Тело, имеющее массу 2 кг движется поступательно со скоростью 36 км/ч. Найдите, какой кинетической энергией оно обладает.
Решение
Прежде чем приступить к вычислению необходимо перевести скорость тела в единицы СИ:
Подставим известные значения в формулу кинетической энергии и выполним расчет:
Ответ: кинетическая энергия тела составляет 100 Джоулей.
Задача 2
Груз массой 0,2 кг прикреплен к пружине, которая закреплена горизонтально. Максимальная скорость колебания 3 м/с. Вычислить максимальную кинетическую энергию тела.
Решение
Воспользуемся выражением определения кинетической энергии:
Ответ: максимальная кинетическая энергия пружины и груза составляет 0,9 Дж.
Задача 3
Найдите среднюю кинетическую энергию поступательного движения молекулы водорода при температуре Т = 280 К.
Решение
Для решения задачи воспользуемся уравнением, связывающим температуру и энергию:
где k – это постоянная Больцмана
Ответ: средняя кинетическая скорость молекулы водорода составляет \(579,6\times10^<-23>\;Дж.\)
Закон сохранения механической энергии
Энергия: что это такое
Если мы погуглим определение слова «Энергия», то скорее всего найдем что-то про формы взаимодействия материи. Это верно, но совершенно непонятно.
Поэтому давайте условимся здесь и сейчас, что энергия — это запас, который пойдет на совершение работы.
Энергия бывает разных видов: механическая, электрическая, внутренняя, гравитационная и так далее. Измеряется она в Джоулях (Дж) и чаще всего обозначается буквой E.
Механическая энергия
Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу.
Она представляет собой совокупность кинетической и потенциальной энергии. Кинетическая энергия — это энергия действия. Потенциальная — ожидания действия.
Представьте, что вы взяли в руки канцелярскую резинку, растянули ее и отпустили. Из растянутого положения резинка просто «полетит», как только вы ей позволите это сделать. В этом процессе в момент натяжения резинка обладает потенциальной энергией, а в момент полета — кинетической.
Еще один примерчик: лыжник скатывается с горы. В самом начале — на вершине — у него максимальная потенциальная энергия, потому что он в режиме ожидания действия (ждущий режим 😂), а внизу горы он уже явно двигается, а не ждет, когда с ним это случится — получается, внизу горы кинетическая энергия.
Кинетическая энергия
Еще разок: кинетическая энергия — это энергия действия. Величина, которая очевиднее всего характеризует действие — это скорость. Соответственно, в формуле кинетической энергии точно должна присутствовать скорость.
Кинетическая энергия
Ек = (m*v^2)/2
Ек — кинетическая энергия [Дж]
Чем быстрее движется тело, тем больше его кинетическая энергия. И наоборот — чем медленнее, тем меньше кинетическая энергия.
Задачка раз
Определить кинетическую энергию собаченьки массой 10 килограмм, если она бежала за мячом с постоянной скоростью 2 м/с.
Решение:
Формула кинетической энергии Ек = (m*v^2)/2
Ответ: кинетическая энергия пёсы равна 20 Дж.
Задачка два
Найти скорость бегущего по опушке гнома, если его масса равна 20 килограммам, а его кинетическая энергия — 40 Дж
Решение:
Формула кинетической энергии Ек = (m*v^2)/2
Ответ: гном бежал со скоростью 2 м/с.
Потенциальная энергия
В отличие от кинетической энергии, потенциальная чаще всего тем меньше, чем скорость больше. Потенциальная энергия — это энергия ожидания действия.
Например, потенциальная энергия у сжатой пружины будет очень велика, потому что такая конструкция может привести к действию, а следовательно — к увеличению кинетической энергии. То же самое происходит, если тело поднять на высоту. Чем выше мы поднимаем тело, тем больше его потенциальная энергия.
Потенциальная энергия деформированной пружины
Еп — потенциальная энергия [Дж]
x — удлинение пружины [м]
Потенциальная энергия
Еп = mgh
Еп — потенциальная энергия [Дж]
g — ускорение свободного падения [м/с^2]
На планете Земля g ≃ 9,8 м/с^2
Задачка раз
Найти потенциальную энергию рака массой 0,1 кг, который свистит на горе высотой 2500 метров. Ускорение свободного падения считать равным 9,8 м/с^2.
Решение:
Формула потенциальной энергии Еп = mgh
Eп = 0,1 * 9,8 * 2500=2450 Дж
Ответ: потенциальная энергия рака, свистящего на горе, равна 2450 Дж.
Задачка два
Найти высоту горки, с которой собирается скатиться лыжник массой 65 килограмм, если его потенциальная энергия равна 637 кДж. Ускорение свободного падения считать равным 9,8 м/с^2.
Решение:
Формула потенциальной энергии Еп = mgh
Переведем 637 кДж в Джоули.
637 кДж = 637000 Дж
h = 637 000/(65 * 9,8) = 1000 м
Ответ: высота горы равна 1000 метров.
Задачка три
Два шара разной массы подняты на разную высоту относительно поверхности стола (см. рисунок). Сравните значения потенциальной энергии шаров E1 и E2. Считать, что потенциальная энергия отсчитывается от уровня крышки стола.
Решение:
Потенциальная энергия вычисляется по формуле: E = mgh
Таким образом, получим, что
Ответ: E1 = E2.
Закон сохранения энергии
В физике и правда ничего не исчезает бесследно. Чтобы это как-то выразить, используют законы сохранения. В случае с энергией — Закон сохранения энергии.
Закон сохранения энергии
Полная механическая энергия замкнутой системы остается постоянной.
Полная механическая энергия — это сумма кинетической и потенциальной энергий. Математически этот закон описывается так:
Закон сохранения энергии
Еполн.мех. = Еп + Eк = const
Еполн.мех. — полная механическая энергия системы [Дж]
Еп — потенциальная энергия [Дж]
Ек — кинетическая энергия [Дж]
const — постоянная величина
Задачка раз
Мяч бросают вертикально вверх с поверхности Земли. Сопротивление воздуха пренебрежимо мало. Как изменится высота подъёма мяча при увеличении начальной скорости мяча в 2 раза?
Решение:
Должен выполняться закон сохранения энергии:
В начальный момент времени высота равна нулю, значит Еп = 0. В этот же момент времени Ек максимальна.
В конечный момент времени все наоборот — кинетическая энергия равна нулю, так как мяч уже не может лететь выше, а вот потенциальная максимальна, так как мяч докинули до максимальной высоты.
Это можно описать соотношением:
Еп1 + Ек1 = Еп2 + Ек2
Разделим на массу левую и правую часть
Из соотношения видно, что высота прямо пропорциональна квадрату начальной скорости, значит при увеличении начальной скорости мяча в два раза, высота должна увеличиться в 4 раза.
Ответ: высота увеличится в 4 раза
Задачка два
Тело массой m, брошенное с поверхности земли вертикально вверх с начальной скоростью v0, поднялось на максимальную высоту h0. Сопротивление воздуха пренебрежимо мало. Чему будет равна полная механическая энергия тела на некоторой промежуточной высоте h?
Решение
По закону сохранения энергии полная механическая энергия изолированной системы остаётся постоянной. В максимальной точке подъёма скорость тела равна нулю, а значит, оно будет обладать исключительно потенциальной энергией Емех = Еп = mgh0.
Таким образом, на некоторой промежуточной высоте h, тело будет обладать и кинетической и потенциальной энергией, но их сумма будет иметь значение Емех = mgh0.
Ответ: Емех = mgh0.
Задачка три
Мяч массой 100 г бросили вертикально вверх с поверхности земли с начальной скоростью 6 м/с. На какой высоте относительно земли мяч имел скорость 2 м/с? Сопротивлением воздуха пренебречь.
Решение:
Переведем массу из граммов в килограммы:
У поверхности земли полная механическая энергия мяча равна его кинетической энергии:
Е = Ек0 = (m*v^2)/2 = (0,1*6^2)/2 = 1,8 Дж
На высоте h потенциальная энергия мяча есть разность полной механической энергии и кинетической энергии:
mgh = E — (m*v^2)/2 = 1,8 — (0,1 * 2^2)/2 = 1,6 Дж
h = E/mg = 1,6/0,1*10 = 1,6 м
Ответ: мяч имел скорость 2 м/с на высоте 1,6 м
Переход механической энергии во внутреннюю
Внутренняя энергия — это сумма кинетической энергии хаотичного теплового движения молекул и потенциальной энергии их взаимодействия. То есть та энергия, которая запасена у тела за счет его собственных параметров.
Часто механическая энергия переходит во внутреннюю. Происходит этот процесс путем совершения механической работы над телом. Например, если сгибать и разгибать проволоку — она будет нагреваться.
Или если кинуть мяч в стену, часть энергии при ударе перейдет во внутреннюю.
Задачка
Какая часть начальной кинетической энергии мяча при ударе о стену перейдет во внутреннюю, если полная механическая энергия вначале в два раза больше, чем в конце?
Решение:
В самом начале у мяча есть только кинетическая энергия, то есть Емех = Ек.
В конце механическая энергия равна половине начальной, то есть Емех/2 = Ек/2
Часть энергии уходит во внутреннюю, значит Еполн = Емех/2 + Евнутр
Емех = Емех/2 + Евнутр
Ответ: во внутреннюю перейдет половина начальной кинетической энергии
Закон сохранения энергии в тепловых процессах
Чтобы закон сохранения энергии для тепловых процессов был сформулирован, было сделано два важных шага. Сначала французский математик и физик Жан Батист Фурье установил один из основных законов теплопроводности. А потом Сади Карно определил, что тепловую энергию можно превратить в механическую.
Вот что сформулировал Фурье:
При переходе теплоты от более горячего тела к более холодному температуры тел постепенно выравниваются и становятся едиными для обоих тел — наступает состояние термодинамического равновесия.
Таким образом, первым важным открытием было открытие того факта, что все протекающие без участия внешних сил тепловые процессы необратимы.
Дальше Карно установил, что тепловую энергию, которой обладает нагретое тело, непосредственно невозможно превратить в механическую энергию для производства работы. Это можно сделать, только если часть тепловой энергии тела с большей температурой передать другому телу с меньшей температурой и, следовательно, нагреть его до более высокой температуры.
Закон сохранения энергии в тепловых процессах
При теплообмене двух или нескольких тел абсолютное количество теплоты, которое отдано более нагретым телом, равно количеству теплоты, которое получено менее нагретым телом.
Математически его можно описать так:
Уравнение теплового баланса
Q отд = Q пол
Qотд — отданное системой количество теплоты [Дж]
Q пол — полученное системой количество теплоты [Дж]
Данное равенство называется уравнением теплового баланса. В реальных опытах обычно получается, что отданное более нагретым телом количество теплоты больше количества теплоты, полученного менее нагретым телом:
Это объясняется тем, что некоторое количество теплоты при теплообмене передаётся окружающему воздуху, а ещё часть — сосуду, в котором происходит теплообмен.
Задачка раз
Сколько граммов спирта нужно сжечь в спиртовке, чтобы нагреть на ней воду массой 580 г на 80 °С, если учесть, что на нагревание пошло 20% затраченной энергии.
Удельная теплота сгорания спирта 2,9·10^7Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг·°С).
Решение:
При нагревании тело получает количество теплоты
где c — удельная теплоемкость вещества
При сгорании тела выделяется энергия
где q — удельная теплота сгорания топлива
По условию задачи нам известно, что на нагревание пошло 20% затраченной энергии.
Ответ: масса сгоревшего топливаа равна 33,6 г.
Задачка два
Какое минимальное количество теплоты необходимо для превращения в воду 500 г льда, взятого при температуре −10 °С? Потерями энергии на нагревание окружающего воздуха пренебречь. Удельная теплоемкость льда равна 2100 Дж/кг*℃, удельная теплота плавления льда равна 3,3*10^5 Дж/кг.
Решение:
Для нагревания льда до температуры плавления необходимо:
Qнагрев = 2100 * 0,5 * (10-0) = 10500 Дж
Для превращения льда в воду:
Qпл = 3,3 * 10^5 * 0,5 = 165000 Дж
Q = Qнагрев + Qпл = 10500 + 165000 = 175500 Дж = 175,5 кДж
Ответ: чтобы превратить 0,5 кг льда в воду при заданных условиях необходимо 175,5 кДж тепла.
Закон cохранения импульса
9 класс, 10 класс, ЕГЭ/ОГЭ
Импульс: что это такое
Как-то раз Рене Декарт (это который придумал ту самую декартову систему координат) решил, что каждый раз считать силу, чтобы описать процессы — как-то лень и сложно.
Для этого нужно ускорение, а оно не всегда очевидно. Тогда он придумал такую величину, как импульс. Импульс можно охарактеризовать, как количество движения — это произведение массы на скорость.
Импульс тела
→ →
p = mv
p — импульс тела [кг*м/с]
Закон сохранения импульса
В физике и правда ничего не исчезает и не появляется из ниоткуда. Импульс — не исключение. В замкнутой изолированной системе (это та, в которой тела взаимодействуют только друг с другом) закон сохранения импульса звучит так:
Закон сохранения импульса
Векторная сумма импульсов тел в замкнутой системе постоянна
А выглядит — вот так:
Закон сохранения импульса
→ → →
p1 + p2 + … + pn = const
p — импульс тела [кг*м/с]
Простая задачка
Мальчик массой m = 45 кг плыл на лодке массой M = 270 кг в озере и решил искупаться. Остановил лодку (совсем остановил, чтобы она не двигалась) и спрыгнул с нее с горизонтально направленной скоростью 3 м/с. С какой скоростью станет двигаться лодка?
Решение:
Запишем закон сохранения импульса для данного процесса.
p0 — это импульс системы мальчик + лодка до того, как мальчик спрыгнул,
p1 — это импульс мальчика после прыжка,
p2 — это импульс лодки после прыжка.
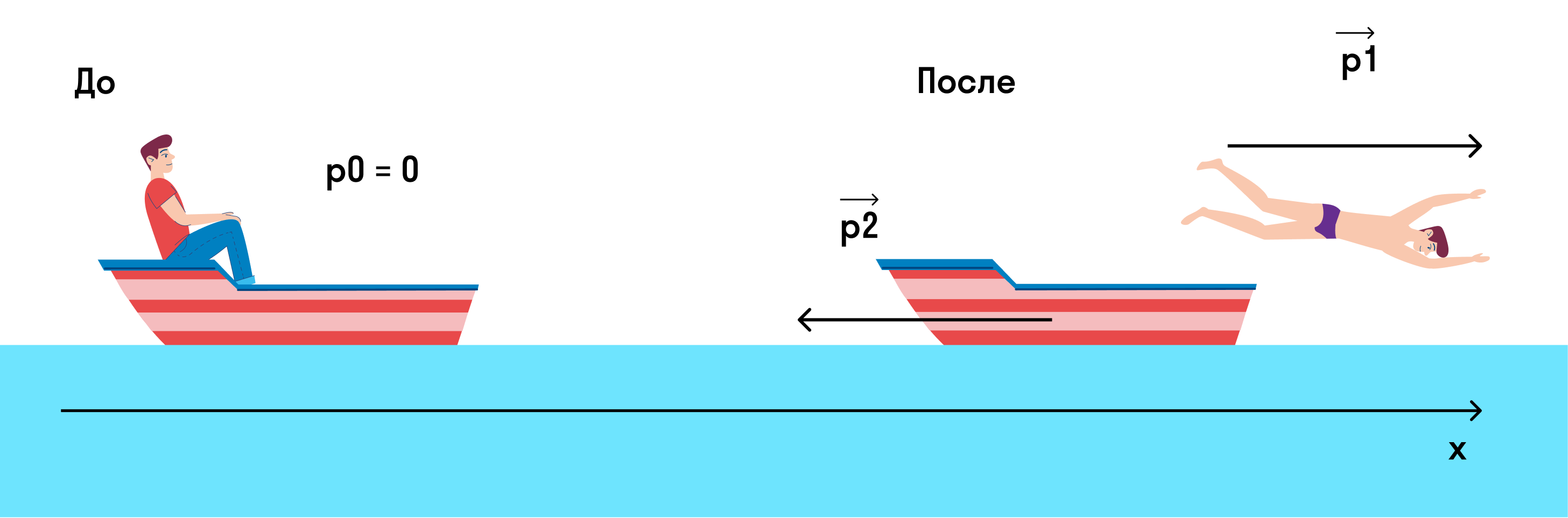
Изобразим на рисунке, что происходило до и после прыжка.
Если мы спроецируем импульсы на ось х, то закон сохранения импульса примет вид
0 = p1 — p2
p1 = p2
Подставим формулу импульса.
mV1 = MV2
Выразим скорость лодки V2:
V2 = mV1/M
Подставим значения:
V2 = 45*3/270 = 3/6 = ½ = 0,5 м/с
Ответ: скорость лодки после прыжка равна 0,5 м/с
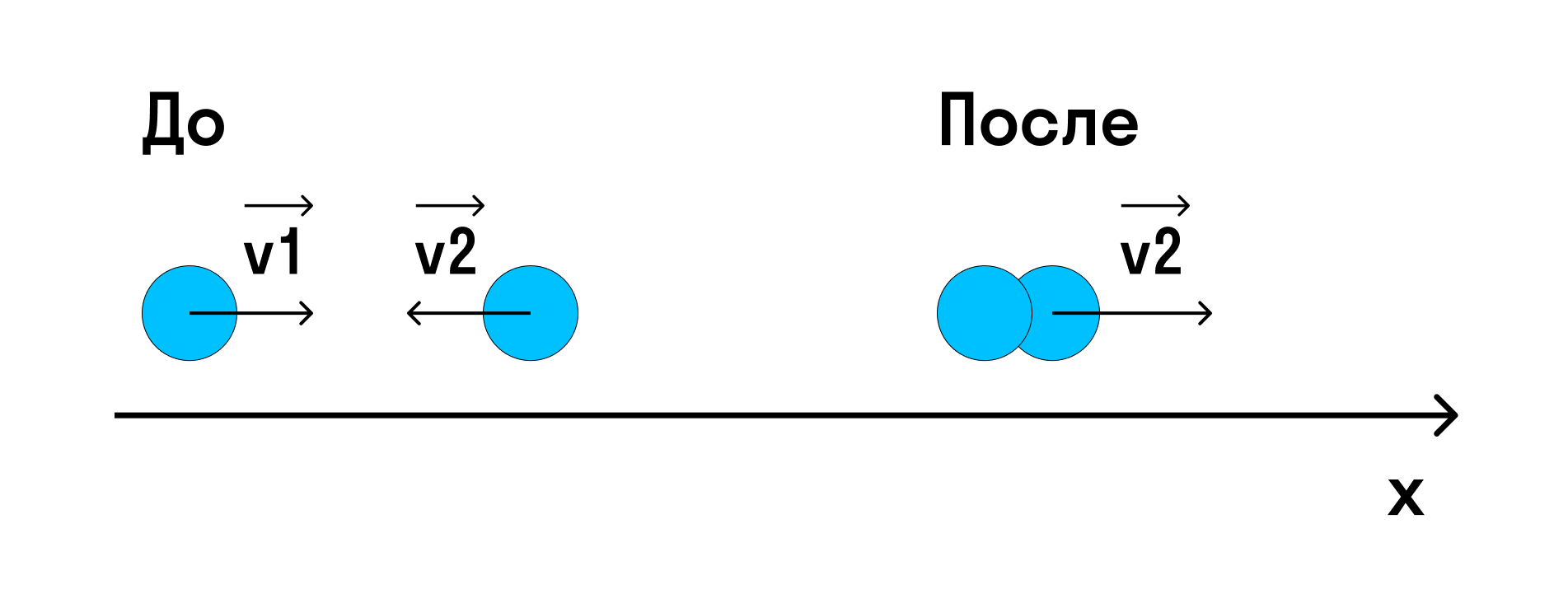
Задачка посложнее
Решение: Для данной системы выполняется закон сохранения импульса:
Импульс системы до удара — это сумма импульсов тел, а после удара — импульс «получившегося» в результате удара тела.
Спроецируем импульсы на ось х:
После неупругого удара получилось одно тело массы m1 + m2, которое движется с искомой скоростью:
m1v1 — mv2 = (m1 + m2) v
Отсюда находим скорость тела, образовавшегося после удара:
v = (m1v1 — mv2)/(m1 + m2)
Переводим массу в килограммы и подставляем значения:
В результате мы получили отрицательное значение скорости. Это значит, что в самом начале на рисунке мы направили скорость после удара неправильно.
Знак минус указывает на то, что слипшиеся тела двигаются в сторону, противоположную оси X. Это никак не влияет на значение получившееся значение.
Ответ: скорость системы тел после соударения равна v = 0,2 м/с.
Второй закон Ньютона в импульсной форме
Второй закон Ньютона в импульсной форме можно получить следующим образом. Пусть для определенности векторы скоростей тела и вектор силы направлены вдоль одной прямой линии, т. е. движение прямолинейное.
Запишем второй закон Ньютона, спроецированный на ось х, сонаправленную с направлением движения и ускорением:
Применим выражение для ускорения
Полученное выражение является пропорцией. Применив основное свойство пропорции, получим такое выражение:
В правой части находится Δv =v —v0 — это разница между конечной и начальной скоростью.
Преобразуем правую часть
Раскрыв скобки, получим
Заменим произведение массы и скорости на импульс:
То есть, вектор Δv⋅m – это вектор Δp.
Тогда второй закон Ньютона в импульсной форме запишем так
Вернемся к векторной форме, чтобы данное выражение было справедливо для любого направления вектора ускорения.
Задачка про белку отлично описывает смысл второго закона Ньютона в импульсной форме
Белка с полными лапками орехов сидит на гладком горизонтальном столе. И вот кто-то бесцеремонно толкает ее к краю стола. Белка понимает законы Ньютона и предотвращает падение. Но как?
Решение:
Чтобы к белке приложить силу, которая будет толкать белку в обратном направлении от края стола, нужно создать соответствующий импульс (вот и второй закон Ньютона в импульсной форме подъехал).
Ну, а чтобы создать импульс, белка может выкинуть орехи в сторону направления движения — тогда по закону сохранения импульса ее собственный импульс будет направлен против направления скорости орехов.
Реактивное движение
В основе движения ракет, салютов и некоторых живых существ: кальмаров, осьминогов, каракатиц и медуз — лежит закон сохранения импульса. В этих случаях движение тела возникает из-за отделения какой-либо его части. Такое движение называется реактивным.
Яркий пример реактивного движения в технике — движение ракеты, когда из нее истекает струя горючего газа, которая образуется при сгорании топлива.
Сила, с которой ракета действует на газы, равна по модулю и противоположна по направлению силе, с которой газы отталкивают от себя ракету:
Сила F2 называется реактивной. Это та сила, которая возникает в процессе отделения части тела. Особенностью реактивной силы является то, что она возникает без взаимодействия с внешними телами.
Закон сохранения импульса позволяет оценить скорость ракеты.
mг vг = mр vр,
где mг — это масса горючего,
vг — скорость горючего,
vр — скорость ракеты.
Отсюда можно выразить скорость ракеты:
Скорость ракеты при реактивном движении
vр = mг vг / mр
mг — это масса горючего [кг]
vг — скорость горючего [м/с]
mр — масса ракеты [кг]
v р — скорость ракеты [м/с]
Эта формула справедлива для случая мгновенного сгорания топлива. Мгновенное сгорание — это теоретическая модель. В реальной жизни топливо сгорает постепенно, так как мгновенное сгорание приводит к взрыву.