Единица измерения deg что это
Градусов в Радианы
Конвертировать из Градусов в Радианы. Введите сумму, которую вы хотите конвертировать и нажмите кнопку конвертировать.
| 1 Градусов = 0.0175 Радианы | 10 Градусов = 0.1745 Радианы | 2500 Градусов = 43.6332 Радианы |
| 2 Градусов = 0.0349 Радианы | 20 Градусов = 0.3491 Радианы | 5000 Градусов = 87.2665 Радианы |
| 3 Градусов = 0.0524 Радианы | 30 Градусов = 0.5236 Радианы | 10000 Градусов = 174.53 Радианы |
| 4 Градусов = 0.0698 Радианы | 40 Градусов = 0.6981 Радианы | 25000 Градусов = 436.33 Радианы |
| 5 Градусов = 0.0873 Радианы | 50 Градусов = 0.8727 Радианы | 50000 Градусов = 872.66 Радианы |
| 6 Градусов = 0.1047 Радианы | 100 Градусов = 1.7453 Радианы | 100000 Градусов = 1745.33 Радианы |
| 7 Градусов = 0.1222 Радианы | 250 Градусов = 4.3633 Радианы | 250000 Градусов = 4363.32 Радианы |
| 8 Градусов = 0.1396 Радианы | 500 Градусов = 8.7266 Радианы | 500000 Градусов = 8726.65 Радианы |
| 9 Градусов = 0.1571 Радианы | 1000 Градусов = 17.4533 Радианы | 1000000 Градусов = 17453.29 Радианы |
Встроить этот конвертер вашу страницу или в блог, скопировав следующий код HTML:
Градус (геометрия)
Градус, минута, секунда — общепринятые единицы измерения плоских углов. Также эти величины используются в картографии для определения координат произвольной точки земной поверхности.
Содержание
Градус
Градус (от лат. gradus — деление шкалы, шаг, ступень) обозначается °. Один оборот равен 360°. В прямом угле, таким образом, 90°, в развёрнутом — 180°.
Деление окружности на 360° придумали аккадцы (вавилоняне).
Минуты и секунды
По аналогии с делением часа как интервала времени градус делят на 60 минут (от лат. minutus — маленький, мелкий; обозначается знаком ′), а минуту — на 60 секунд (от лат. secunda divisio — второе деление; обозначается знаком ″). Корни такого деления лежат в Древнем Вавилоне, где использовалась шестидесятеричная система счисления.
Угловая секунда
Использование
Угловая секунда (обозначается ″) используется в астрономии при измерении плоских углов в градусных мерах. При измерении углов в часовых мерах (в частности, для определения прямого восхождения) используется единица измерения «секунда» (обозначается с ). Соотношение между этими величинами определяется формулой 1 c = 15″. [3]
Дольные единицы
| единица | величина | обозначение | аббревиатура | радиан (прибл.) |
|---|---|---|---|---|
| градус | 1/360 окружности | ° | deg | 17,4532925 mrad |
| минута | 1/60 градуса | ′ | arcmin, amin,  , MOA , MOA | 290,8882087 µrad |
| секунда | 1/60 минуты | ″ | arcsec | 4,8481368 µrad |
| миллисекунда | 1/1000 секунды | mas | 4,8481368 nrad | |
| микросекунда | 1 × 10 −6 секунды | μas | 4,8481368 prad |
Для наблюдения астрономических объектов под такими сверхмалыми углами астрономы прибегают к методу интерферометрии, при котором сигналы, принимаемые несколькими разнесёнными радиотелескопами, комбинируются в процессе апертурного синтеза. Так, используя методику интерферометрии со сверхдлинной базой, астрономы получили возможность измерить собственное движение галактики Треугольника. [источник не указан 168 дней]
В градусах
Что такое «произвольная» единица измерения и что она измеряет
Вы не задавались вопросом, почему в градусах измеряют настолько не связанные между собой вещи — углы и температуру? Скажем больше, градусами меряют плотность жидкости и качество молока и (да, мы не забыли) долю спирта. Gradus — латинское слово, означающее шаг, ступень или степень. Иными словами, у градуса, в отличие от метрических единиц измерения, нет конкретной величины, и он не соответствует никакому эталону, привязанному к тем или иным физическим параметрам. При этом размер градуса можно всякий раз устанавливать по-разному, и ничего не изменится. Кому и зачем могла понадобиться такая единица измерения? Давайте разбираться.
Со школы все мы знаем, что в окружности содержится ровно 360 градусов. Но почему именно 360? Ответить на этот вопрос можно по-разному.
По одной версии, древние астрономы, скорее всего персы и каппадокийцы, заметили, что солнце оказывается в одной и той же точке небосвода лишь один раз в 365 дней. Они объяснили это тем, что солнце совершает полный оборот вокруг земли за год и возвращается в исходную точку.
Возможно, они округлили число 365, а может, и просто пропустили пять дней, но в итоге заключили: солнце сдвигается на одну трехсот шестидесятую долю окружности в день.
Другая теория объясняет 360-градусный полный угол совсем другими причинами. Шумеры и вавилоняне пользовались (не самой удобной) шестидесятеричной системой счисления. Большие числа они считали шестидесятками (например, число 1020 это 17 шестидесятков).
Знаки шумерской шестидесятиричной системы счисления
Вписав в окружность правильный шестиугольник, вавилоняне заметили, что в круг отлично помещаются шесть равносторонних треугольников. Каждому треугольнику они приписывали по шестидесятку. В итоге, шесть треугольников по шестидесятку дали известные 360 градусов.
Шестидесятизначная система объясняет и деление градуса на 60 минут (‘) и 3600 секунд (“). Знак, которым мы сегодня обозначаем градусы (°), впервые был использован в математике в 1569 году, по аналогии с верхним штриховым индексом для минут и секунд.
Независимо от истории, полный угол в 360 градусов — лучший вариант из возможных, ведь 360 — сверхсоставное число (натуральное число, с бoльшим числом делителей, чем все предыдущие). Оно делится на все числа от 1 до 10 за исключением семи, а еще и на: 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120 и 180. На такое количество частей вы можете разделить окружность простым вычислением в уме.
Геометрические градусы прошли проверку временем и оказались самой удобной единицей измерения углов. Но есть и другие.
Так, если у вас есть инженерный калькулятор, то, переключаясь между градусами (DEG) и радианами (RAD), вы, возможно, попадали в режим GRAD — это исчисление в градах (или гонах). Один град — это одна сотая часть прямого угла, а значит, полный угол равен 400 град.
Такая единица измерения появилась во времена Французской революции вместе с метрической системой и быстро всех запутала. Кроме проблем с названием, — в некоторых странах grad обозначали привычные градусы, — возникли трудности и с вычислением.
Например, как известно, углы равностороннего треугольника равны друг другу и составляют 60 градусов. Переведем это в грады — 66 целых и шесть в периоде, ужасно неудобно.
В отличие от метрической системы, без которой трудно представить нашу жизнь, вычисления в градах оказались не самыми простыми, сейчас их практически нигде не используют.
Но свой след в истории они оставили — именно благодаря градам стоградусная температурная шкала получила название шкалы Цельсия.
Температура
Как ни странно, температурные шкалы появились гораздо раньше термометров. Создателем первой шкалы можно считать Галена — древнеримского медика, хирурга и философа.
Гален утверждал, что существует некая нейтральная температура — он определил ее как температуру смеси одинакового количества кипящей воды и льда. От нейтральной температуры он отсчитал по четыре шага (ступени) в сторону тепла и холода.
Шведский теолог и физик Иоганн Хаслер на основании работ Галена построил таблицу температуры, опубликованную на страницах труда «De Logistica Medica problematis novem» в 1578 году. Он отложил те же четыре шага тепла и холода по разные стороны от нейтральной температуры, а также заметил, что шкалу можно заменить на последовательность чисел от единицы до девяти.
В таблице значения температуры называются просто «номерами», но в тексте Хаслер использует слово «градус». Нейтральная температура в его системе будет соответствовать числу пять.
Таблица температуры Иоганна Хаслера. Слева направо: первый столбец — шкала Хаслера, второй — шкала Галена, следующие столбцы связаны с рецептами лекарств
Первое устройство, похожее на современный термометр, создал Галилео Галилей приблизительно в 1597 году. Вслед за этим ученые почти 200 лет искали универсальную, удобную и точную шкалу температур.
Например, в 1701 году Исаак Ньютон в опубликованной анонимно работе (в ней он уже использует слово gradus для обозначения единиц тепла) предлагат 18 реперных точек, часть из которых формирует геометрическую, а другая — арифметическую прогрессии. В градусах Ньютона точка замерзания воды равна 0 градусов, а температура человеческого тела — 12 градусов.
В том же году известный астроном Оле Ремер (первым измеривший скорость света) предложил свой вариант. Нулем своей шкалы он выбрал температуру соленой воды со льдом, а вот температуру кипения воды — снова это магическое число — он обозначил как 60 градусов. Эту шкалу позаимствовал знакомый Ремера, Габриэль Фаренгейт.
Фаренгейт избавился от неудобных дробей, возникавших при измерении температуры человеческого тела (22,5 градуса) и замерзания пресной воды (7,5 градуса), заменив их на 24 и 8 градусов соответственно. Вода стала кипеть при 64 градусах Фаренгейта.
Некоторое время он производил термометры с такой шкалой, но потом, в 1724 году, умножил ее на 4. По одной версии, Фаренгейт просто хотел сделать шкалу точнее, поэтому увеличил количество рисок на градуснике, по другой — он сделал это, чтобы увеличение температуры на один Фаренгейт приводило к увеличению объема ртути ровно на одну десятитысячную.
Так появилась знаменитая шкала Фаренгейта, которой люди пользуются и сегодня. Некоторое время она была лучшей из возможных, но затем ей смену пришел более совершенный вариант. Хотя жители США навряд ли согласились бы с нами.
Жозеф Николя Делиль пошел несколько другим путем. Он выбрал всего одну реперную точку, температуру кипения воды, и обозначил ее за ноль. Градуировать шкалу он решил по расширению ртути в термометре — понижение температуры, приводящее к уменьшению объема ртути на одну стотысячную, Делиль обозначил за один градус.
Температура замерзания воды в таком случае — 2400 градусов, шкала оказалась излишне мелкой, поэтому в 1738 году Иосия Вейтбрехт изменил ее. Он задал температуру замерзания воды в 150 градусов.
Такие термометры стали удобными и получили широкое распространение. Ими примерно сто лет пользовались в России, Ломоносов использовал термометр Делиля (правда, перевернув шкалу) в своих опытах.
Только в этот момент на сцене появляется Андерс Цельсий. В 1741 году он наносит на термометр Делиля свою шкалу — 0 градусов в точке кипения и 100 градусов в точке замерзания воды. Перевернули шкалу (скорее всего, это сделал Карл Линней) через год после смерти Цельсия (он умер в 1744 году от туберкулеза).
Кстати, к 1745 году уже существовал термометр с нулем в точке замерзания и сотней градусов в точке кипения воды. Он называется термометром Лиона, его изобретатель — французский физик Жан-Пьер Кристен.
Заслуга Цельсия в другом — он провел эксперименты, продемонстрировавшие, что температура плавления льда практически не зависит от давления. Более того, он с высокой точностью определил, как температура кипения воды изменяется в зависимости от атмосферного давления.
Цельсий предложил калибровать ноль своей температурной шкалы (в тот момент, точку кипения воды) по атмосферному давлению, определить которое можно по среднему уровню моря.
Эта калибровка наконец сделала термометры по-настоящему универсальными. Вероятно, именно поэтому прогноз погоды, который вы смотрели сегодня утром, был в градусах Цельсия.
Но стоградусную температурную шкалу назвали в честь Цельсия только в 1948 году. До этого она так и называлась — стоградусной температурной (centigrade temperature scale). Но во французском (где использовали грады) термин centigrade уже был занят в геометрии.
Чтобы избежать путаницы, Международное бюро мер и весов переименовало шкалу в честь Андерса Цельсия. Так градусы температуры стали градусами Цельсия.
Диаграмма перевода температур, на которой указаны основные температурные шкалы
Единицы размеров в CSS
Здесь будут рассматриваться только единицы размеров, которыми мы пользуемся чаще всего. Подробное описание можно найти в спецификации W3C Distance Units: the type.
Абсолютные единицы измерения
| cm | сантиметр | 1cm = 96px/2.54 ≈ 37,795px |
| mm | миллиметр | 1mm = 1/10 от 1cm |
| q | четверь миллиметра | 1q = 1/40 от 1cm = 0.25mm ≈ 0.945px |
| in | дюйм | 1in = 2.54cm = 96px |
| pc | пика | 1pc = 1/6 от 1in |
| pt | пункт, точка | 1pt = 1/72 от 1in |
| px | пиксель | 1px = 1/96 от 1in, 0.75 от pt |
Абсолютные единицы относительны друг для друга (соотношения в последней колонке), но все они привязаны к конкретным величинам.
Для печатных устройств сантиметры, миллиметры и дюймы должны быть равны своим обычным значениям, но для экранов это будет не так:
Я попыталась разными способами получить полоску длиной 10 сантиметров. Все полоски равны друг другу, но ни одна не равна 10 сантиметрам, если приложить линейку к экрану. Проверила на двух мониторах: на одном они короче, на другом — длиннее.
Позже появились ретиновые дисплеи с повышенной плотностью пикселей, и тогда CSS-пиксели, которые мы используем, перестали соответствовать физическим пикселям экрана, теперь это виртуальная единица, размер которой определяется устройством вывода. Для нас это не играет особой роли кроме как при работе с изображениями, когда для ретины нужно подготовить дополнительный набор картинок. Все размеры, заданные в пикселях, будут корректно отображены на экране вне зависимости от того, сколько физических пикселей для этого потребуется.
На сегодняшний момент соотношение физических единиц к точкам экрана утратило прежний смысл, но осталось зафиксированым в спецификации для сохранения обратной совместимости и упрощения конвертации одних единиц в другие.
При этом важно помнить, что раз CSS-пиксели уже не соответствуют физическим точкам экрана, сантиметры и дюймы при выводе на экран тоже не будут не соответствовать своим реальным размерам, об этом есть и в спецификации:
If the anchor unit is the pixel unit, the physical units might not match their physical measurements. Alternatively if the anchor unit is a physical unit, the pixel unit might not map to a whole number of device pixels.
То есть, если использовать дюймы для вёрстки веб-страниц, один дюйм всегда будет равен 96 пикселям, но никогда — реальной физической единице:
Таким образом, главное в абсолютных единицах — контекст использования:
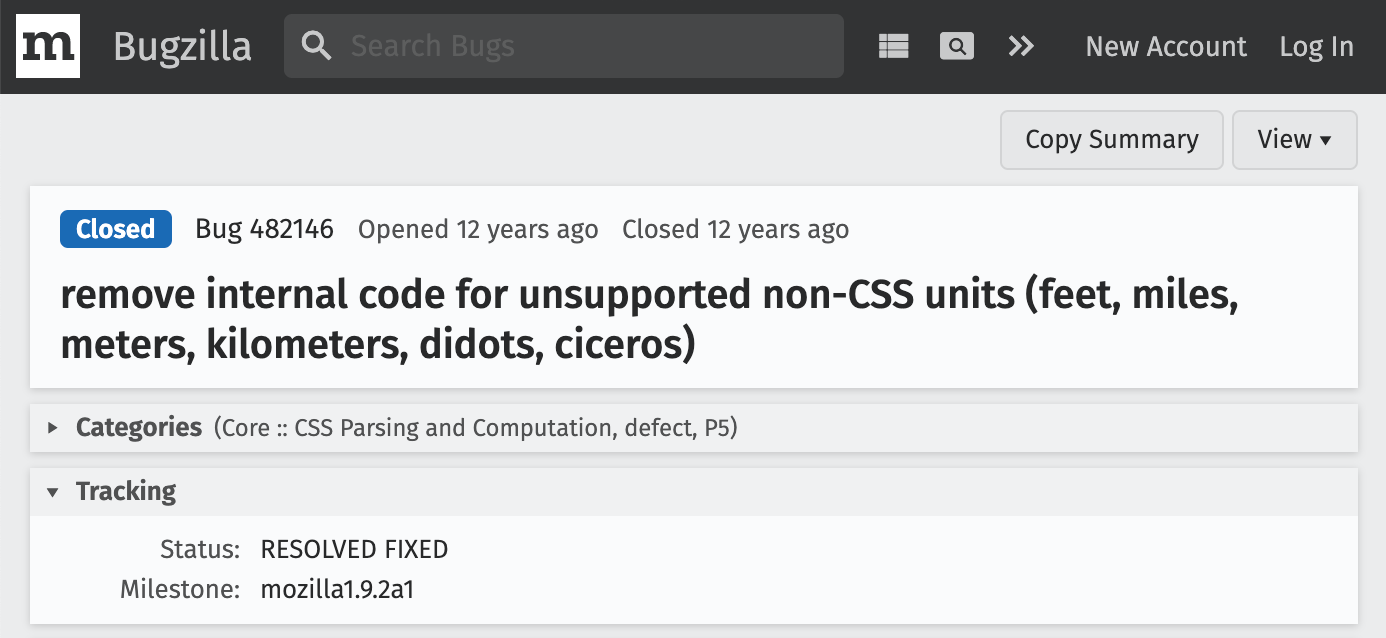
Пока копалась в истории единиц измерения, выяснилось, что во внутреннем коде Gecko когда-то была поддержка километров, удалили в 2009-м:
Пример такого использования я подсмотрела в этом демо. Открывайте осторожно, может повиснуть браузер. Попытка посмотреть стили в веб-инспекторе вешает его почти гарантированно, поэтому лучше посмотрите исходный код страницы. Скриншот:
Вес стилей демо — 4.5Mb, а если бы там вместо q были пиксели, стили весили бы на 300Kb больше.
Относительные единицы измерения
Относительные единицы измерения вычисляются на основе каких-то других величин: размера шрифта или размера экрана, и могут динамически меняться вместе с ними.
Единицы измерения, привязанные к шрифту
| em | размер шрифта элемента |
| ex | высота x в нижнем регистре |
| ch | ширина 0 (ZERO, U+0030) |
| rem | размер шрифта корневого элемента |
Чтобы увидеть это вживую, возьмем такой код:
Получилось вот что:
Размер em нигде не зафиксирован, и вычисляется в момент использования на основе размера шрифта родителя. Например, если задать размер шрифта вот таким образом:
а потом вложить несколько дивов один в другой, размер шрифта каждого следующего дива будет меньше предыдущего:
Об этом нужно помнить, если вы захотите задавать в em размеры переиспользуемых компонентов: при вкладывании элементов друг в друга вычисленное значение em может оказаться не тем, что хотелось бы получить.
ex точно также как и em наследует размер шрифта родителя:
Эрик Мейер предостерегает от попыток использовать ch для задания ширины контейнера в символах, потому что это не работает как ожидается. В демо ниже ширина каждого блока с текстом задана вот таким образом:
Если rem можно было бы переопределять в любом месте, текст бы увеличился, но этого не произошло:
Это позволяет делать компоненты, размеры которых привязаны к базовому размеру шрифта, но не зависят от вложенности элементов друг в друга.
Единицы измерения, привязанные к размерам экрана
| vw | 1% ширины вьюпорта |
| vh | 1% высоты вьюпорта |
| vmin | 1% от меньшего из vw и vh |
| vmax | 1% от большего из vw и vh |
Эти единицы предназначены для создания элементов, размер которых должен зависеть от размера окна (вьюпорта).
100vh — это высота вьюпорта, очень удобно для элементов, которые должны растягиваться на всю страницу. Вот пример простой галереи, где каждая картинка будет полностью занимать один экран независимо от размеров окна браузера:
Размеры картинок задаются вот таким образом:
Правда, тут есть проблема: 100vw — это ширина всего окна вместе с полосой прокрутки, а доступная для контента ширина окна полосу прокрутки не включает, из-за чего при попытке задать элементам ширину вьюпорта появится горизонтальный скролл:
Проблема с полосами прокрутки будет видна только в десктопных браузерах, потому что на мобильных скроллбар размещается поверх страницы и не занимает пространство.
Если вы верстаете на MacOS, и полосы прокрутки исчезают сами по себе, выберите в System Perefences/General опцию «Показывать всегда», это позволит верстать страницы сразу с учетом сколлбаров:
Используя vw и vh можно делать полностью резиновые элементы, которые будут сами подстраиваться под размер окна, например, так:
Лучше всего открыть это демо в отдельной вкладке и порастягивать окно браузера.
С помощью vmin можно сделать элемент, который всегда будет целиком помещаться в экран, сохраняя пропорции:
Это демо тоже лучше смотреть в отдельной вкладке, попробуйте порастягивать окно по вертикали и по горизонтали.
Пример с единицами вьюпорта ведёт себя совершенно логично, потому что масштабирование не меняет размер окна. Об этой особенности нужно помнить, если вы захотите использовать единицы вьюпорта для задания размера текста — пользователь не сможет сделать такой текст покрупнее.
В качестве решения предлагается примешивать единицы вьюпорта к относительным единицам измерения, привязанным к размеру шрифта, например, так:
Вживую можно потестить здесь, пример взят из этой статьи. Больше про управление размером шрифта с помощью единиц вьюпорта можно почитать тут.
За дополнение про особенности масштабирования спасибо @bekharsky.
У единиц, привязанных к размерам вьюпорта, могут быть проблемы с поддержкой в IE включая 11-й, поэтому обязательно проверяйте код в действующем браузере.
В спецификации описано немного больше единиц измерения, например:
Но в данный момент они нигде не поддерживаются, поэтому в статье не рассматриваются.
Спасибо Илье Стрельцыну за полезные ссылки.
Радианы в Градусов
Конвертировать из Радианы в Градусов. Введите сумму, которую вы хотите конвертировать и нажмите кнопку конвертировать.
| 1 Радианы = 57.2958 Градусов | 10 Радианы = 572.96 Градусов | 2500 Радианы = 143239.45 Градусов |
| 2 Радианы = 114.59 Градусов | 20 Радианы = 1145.92 Градусов | 5000 Радианы = 286478.9 Градусов |
| 3 Радианы = 171.89 Градусов | 30 Радианы = 1718.87 Градусов | 10000 Радианы = 572957.8 Градусов |
| 4 Радианы = 229.18 Градусов | 40 Радианы = 2291.83 Градусов | 25000 Радианы = 1432394.49 Градусов |
| 5 Радианы = 286.48 Градусов | 50 Радианы = 2864.79 Градусов | 50000 Радианы = 2864788.98 Градусов |
| 6 Радианы = 343.77 Градусов | 100 Радианы = 5729.58 Градусов | 100000 Радианы = 5729577.95 Градусов |
| 7 Радианы = 401.07 Градусов | 250 Радианы = 14323.94 Градусов | 250000 Радианы = 14323944.88 Градусов |
| 8 Радианы = 458.37 Градусов | 500 Радианы = 28647.89 Градусов | 500000 Радианы = 28647889.76 Градусов |
| 9 Радианы = 515.66 Градусов | 1000 Радианы = 57295.78 Градусов | 1000000 Радианы = 57295779.51 Градусов |
Встроить этот конвертер вашу страницу или в блог, скопировав следующий код HTML: