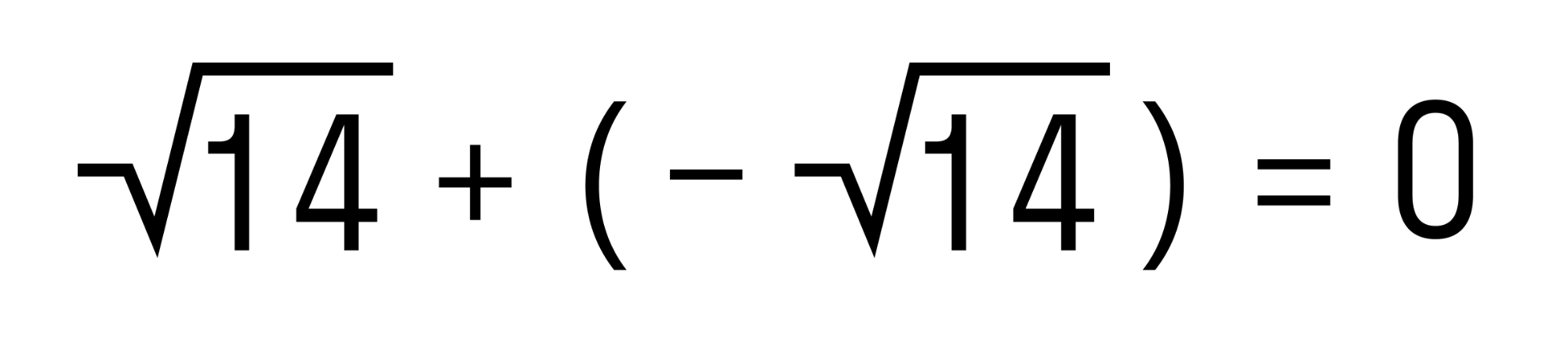Если знаки разные то что нужно делать

Сложение и вычитание целых чисел

Сложение

При сложении двух целых чисел с одинаковым знаком складываются их абсолютные величины и перед суммой ставится их общий знак.

Из данных примеров следует, что в результате сложения двух положительных чисел получится положительное число, а в результате сложения двух отрицательных чисел – отрицательное число.

При сложении двух целых чисел с разными знаками нужно взять их абсолютные величины и из большей вычесть меньшую, в результате ставится знак того числа, у которого абсолютная величина больше.

Другими словами, можно просто, не обращая внимания на знаки, вычесть из большего числа меньшее и у получившегося результата поставить знак большего числа:

Из данных примеров следует, что в результате сложения двух чисел с разными знаками может получится как положительное, так и отрицательное число.

Вычитание

Вычитание одного целого числа из другого можно заменить сложением, при этом уменьшаемое берётся со своим знаком, а вычитаемое с противоположным.

Из данных примеров следует, что, чтобы из одного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому.

При решении выражений, содержащих и сложение, и вычитание, можно сначала заменить вычитание сложением, затем отдельно сложить положительные и отрицательные слагаемые, а потом найти сумму получившихся чисел.

Решение: Заменим вычитание на сложение:

сгруппируем слагаемые по их знакам и сложим отдельно положительные и отрицательные числа:

(12 + 41) + ((-18) + (-9)) = 53 + (-27).

Теперь осталось только найти сумму двух получившихся результатов:

Источник

Сложение чисел с разными знаками

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные определения

Целые числа — это множество чисел, которые состоят из натуральных чисел, целых отрицательных чисел и нуля.

Положительные целые числа — это целые числа со знаком «плюс». Они всегда больше нуля. Примеры положительных целых чисел: 11, 500, 1387.

У каждого положительного числа есть число-близнец, которое отличается только тем, что перед ним стоит знак минус. Такие числа называются противоположными.

Противоположные числа не равны друг другу, но у них есть общее — модуль. Модуль у противоположных чисел одинаковый: у положительного числа он равен самому числу, а у отрицательного — противоположному, то есть положительному. Например:

Действительные числа — это числа, которые могут быть записаны в виде конечной или бесконечной десятичной дроби.

Рациональные числа — это числа, которые можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль.

Правило сложения чисел с разными знаками

Положительное число можно рассматривать как доход, а отрицательное — как расходы или долг. Чтобы понять, сколько мы заработали или потратили, нужно смотреть на модули этих чисел.

Например, родители выдали триста рублей на карманные расходы. Если в конце недели у нас осталось немного денег — значит расходов было меньше, чем дохож. А если нам пришлось попросить еще 50 рублей на наклейки — расходы привысили доход. Если же расходы равны доходам, то у нас будет нулевой остаток.

А теперь сформулируем правило сложения чисел с разными знаками.

Чтобы сложить положительное и отрицательное число, нужно:

Это правило сводит сложение чисел с разными знаками к вычитанию из большего положительного числа меньшее число. В результате сложения положительного и отрицательного числа может получиться: положительное число, отрицательное число или нуль.

Повторим еще раз. Чтобы сложить числа с разными знаками:

Алгоритм сложения чисел с разными знаками справедлива для целых чисел, для рациональных чисел и для действительных чисел.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Примеры сложения чисел с разными знаками

Сложение чисел с разными знаками требует внимательности и последовательности. Рассмотрим примеры по правилу выше:

Нам нужно сложить числа с разными знаками. Выполним все шаги по правилу сложения положительного и отрицательного числа.

Чтобы сложить рациональные числа с разными знаками, которые не являются целыми, их следует представить в виде обыкновенных или десятичных дробей.

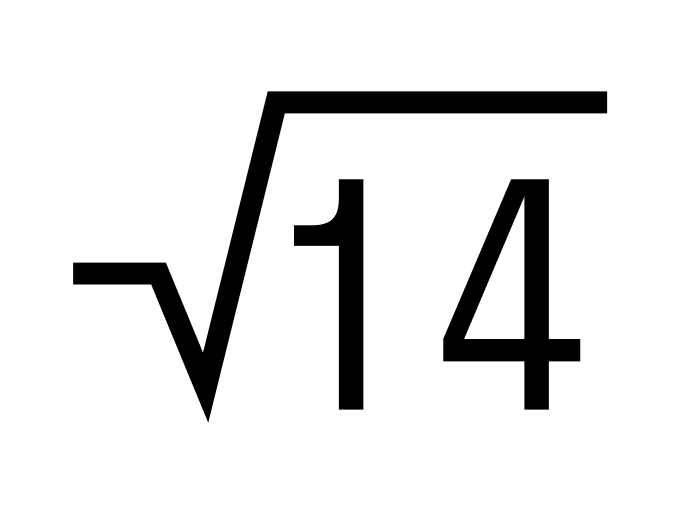
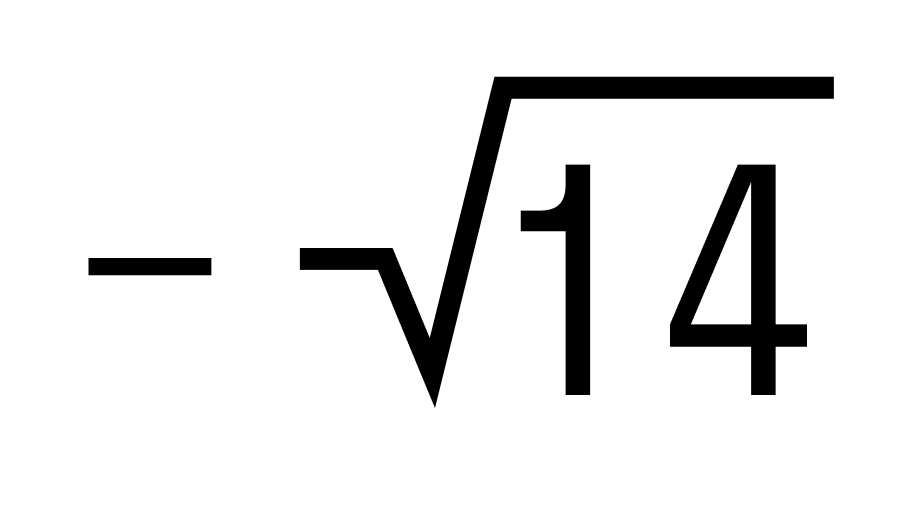
Пример 3. Чему равна сумма чисел и ?

Замечаем, что у складываемых чисел разные знаки, а их модули равны. Значит эти числа являются противоположными, а сумма противоположных чисел равна нулю.

Получается вот так:

Важно помнить, что при сложении действительных чисел с разными знаками результат можно записывать не в виде бесконечной десятичной дроби, а в виде числового выражения, которое содержит корни, степени, логарифмы и прочее.

Источник

Вычитание чисел с разными знаками: правила, примеры

Данная статья посвящена числам с разными знаками. Мы будем разбирать материал и пытаться выполнять вычитание между этими числами. В параграфе мы познакомимся с основными понятиями и правилами, которые пригодятся во время решения упражнений и задач. Также в статье представлены подробно разобранные примеры, которые помогут лучше понять материал.

Как правильно выполнять вычитание

Для того, чтобы лучше понять процесс вычитания, следует начать с основных определений.

Данное правило, которое применяется для вычитания чисел с разными знаками, позволяет работать как с положительными, так и с отрицательными числами. Также можно производить процесс вычитания из отрицательного числа из положительного, которое переходит в сложение.

Для того, чтобы закрепить полученную информацию, мы рассмотрим типичные примеры и на практике рассмотрим правило вычитания для чисел с разными знаками.

Примеры упражнений на вычитание

Закрепим материал, рассмотрев типичные примеры.

Для того, чтобы выполнять вычитание дробей, необходимо представлять числа в виде обыкновенных или десятичных дробей. Это зависит от того, с числами какого вида будет удобнее проводить вычисления.

Когда какое-либо число представлено в виде квадратного корня, логарифма, основной и тригонометрических функций, то зачастую результат вычитания может быть записан в виде числового выражения. Чтобы пояснить данное правило, рассмотрим следующий пример.

Значение полученного выражения может быть вычислено максимально точно только в том случае, если это необходимо. Для подробной информации можно изучить другие разделы, связанные с данной темой.

Источник

Математика

Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет

С этой картой можно накопить на мечту, жми ⇒

Именная карта банка для детей
с крутым дизайном, +200 бонусов

Закажи свою собственную карту банка и получи бонусы

План урока:

Сложение и вычитание отрицательных чисел

Давайте вспомним любимую многими сказку «Буратино» и разберем задачу с участием любимых персонажей.

Возвращаемся к решению задачи.

Теперь, правильно запишем и суммируем известные данные.

Рассмотрим еще одно задание.

Чтобы вычислить сумму двух значений со знаком «минус», достаточно суммировать их модули, и перед полученной цифрой записать «-».

Запомни! Если складываем два отрицательных числа, то суммируем их модули, а перед результатом сложения записываем «-».

Сложение чисел с разными знаками

Используем рассмотренный алгоритм при выполнении действий.

Суммируем-3 и 10. Для этого:

Помним, что большее значение модуля имеет отрицательное слагаемое (-28), поэтому перед результатом нужно будет поставить знак «минус». Теперь, находим разность большего и меньшего значения модуля (28-17) и записываем математическое выражение:

Учитывая рассмотренные примеры, можно сказать, что:

любое числовое значение от прибавления к нему положительного числа, всегда становится больше, а от прибавления отрицательного числа только меньше.

Докажем справедливость данного правила, вычислив выражение и сравнив уменьшаемое с полученной суммой:-150+50.

Чтобы найти значение выражения нужно определить модули (150 и 50), оставив знак«-» модуля большего слагаемого, от большего значения отнимаем меньшее:

Сравним найденное значение выражения (-100) с уменьшаемым (-150), используя правило сравнения чисел с отрицательным знаком:

При сравнении цифровых значений со знаком «минус», меньшим будет то, чей модуль больше.

-150 1 Сложить их модули, а перед результатом поставить знак «плюс»

Источник

Сложение чисел с разными знаками: правило, примеры

В этом материале мы расскажем, как правильно выполнять сложение отрицательного и положительного числа. Сначала мы приведем основное правило такого сложения, а потом покажем, как оно применяется при решении задач.

Основное правило сложения положительных и отрицательных чисел

Мы уже говорили ранее, что положительное число можно рассматривать как доход, а отрицательное – как убыток. Чтобы узнать величину дохода и расхода, надо смотреть на модули этих чисел. Если в итоге окажется, что наши расходы превышают доходы, то после их взаимного учета мы останемся должны, а если наоборот, то мы останемся в плюсе. Если же расходы равны доходам, то у нас будет нулевой остаток.

Используя приведенные выше рассуждения, можно вывести основное правило сложения чисел с разными знаками.

Для сложения положительного числа с отрицательным необходимо найти их модули и выполнить сравнение. Если значения окажутся равны, то мы имеем два слагаемых, которые являются противоположными числами, и их сумма будет нулевой. Если же они не равны, то нам надо учесть, что результат будет иметь тот же знак, что и большее число.

Таким образом, сложение в данном случае сводится к вычитанию из большего числа меньшего. Итог этого действия может быть разным: мы можем получить как положительное, так и отрицательное число. Нулевой результат тоже возможен.

Это правило распространяется на целые, рациональные и действительные числа.

Задачи на сложение положительного числа с отрицательным

Разберем, как применять на практике правило, озвученное выше. Возьмем для начала простой пример.

Решение

Если в условиях задачи стоят рациональные числа с разными знаками, не являющиеся при этом целыми, то для удобства расчетов нужно представить их в виде десятичных или обыкновенных дробей. Возьмем такую задачу и решим ее.

Решение

Первым делом переведем смешанное число в обыкновенную дробь. Если вы не помните, как это делается, перечитайте соответствующую статью.

Далее вычтем из большего модуля меньший (см. материал о том, как найти разность дробей с одинаковыми знаменателями):

Запишем весь ход решения:

Решение

Источник