Евклидова геометрия что это такое

Евклидова (элементарная) геометрия

Евклидова геометрия — это геометрическая теория, основанная на системе аксиом, которая была впервые изложена в третьем веке до нашей эры великим древнегреческим математиком Евклидом в грандиозном научном труде «Начала».

Система аксиом Евклида базируется на основных геометрические понятиях таких, как точка, прямая, плоскость, движение, а также на следующие отношения: «точка лежит на прямой на плоскости», «точка лежит между двумя другими».

В «Началах» Евклид представил следующую аксиоматику:

Тщательное изучение аксиоматики Евклида во второй половине XIX века показало её неполноту. В 1899 году Д. Гилберт предложил первую строгую аксиоматику евклидовой геометрии. Впоследствии еще не раз ученые предпринимали попытки усовершенствовать аксиоматику евклидовой геометрии. Кроме аксиоматики Гилберта, известными считаются: аксиоматики Тарского и аксиоматики Биргофа, которая состоит всего лишь из 4 аксиом.

В современной трактовке система аксиом Евклида может быть разделена на пять групп:

Евклидова геометрия стала результатом систематизации и обобщения наглядных представлений человека об окружающем мире. Углубленное проникновение в суть геометрии привело к более абстрактному пониманию науки. Более поздние достижения и открытие показали, что наши представления о пространстве являются априорными, то есть чисто умозрительные. Таким образом было поставлено под сомнение существование единственной геометрии. бурное развитие физики и астрономии, доказало, что евклидова геометрия описывает структуру окружающего пространства, но вовсе не способна описать свойства пространства, связанные с перемещениями тел со скоростями, близкими к световой. Русский математик Н. И. Лобачевский разработал новую неевклидову геометрию, которая приблизилась к реальному описанию физического пространства.

Источник

Евклидова геометрия

Евкли́дова геоме́трия (или элементарная геометрия) — геометрическая теория, основанная на системе аксиом, впервые изложенной в «Началах» Евклида (III век до н. э.).

Содержание

Основные сведения

Элементарная геометрия — геометрия, определяемая в основном группой перемещений (изометрий) и группой подобия. Однако содержание элементарной геометрии не исчерпывается указанными преобразованиями. Так, к элементарной геометрии также относят преобразование инверсии, вопросы сферической геометрии, элементы геометрических построений, теорию измерения геометрических величин и другие вопросы.

Элементарную геометрию часто называют евклидовой геометрией, так как первоначальное и систематическое её изложение, хотя и недостаточно строгое, было в «Началах» Евклида. Первая строгая аксиоматика элементарной геометрии была дана Гильбертом. Элементарная геометрия изучается в средней общеобразовательной школе.

Аксиоматика

Проблема полной аксиоматизации элементарной геометрии — одна из проблем геометрии, возникшая в Древней Греции в связи с критикой этой первой попытки построить полную систему аксиом так, чтобы все утверждения евклидовой геометрии следовали из этих аксиом чисто логическим выводом без наглядности чертежей.

В «Началах» Евклида была дана следующая аксиоматика:

Исследование системы аксиом Евклида во второй половине XIX века показало её неполноту.

В 1899 году Гильберт предложил первую достаточно строгую аксиоматику евклидовой геометрии. Попытки улучшения евклидовой аксиоматики предпринимались до Гильберта Пашем, Шуром, Пеано, Веронезе, однако подход Гильберта, при всей его консервативности в выборе понятий, оказался более успешным.

Существуют и другие современные аксиоматики, наиболее известные:

См. также

Литература

Полезное

Смотреть что такое «Евклидова геометрия» в других словарях:

ЕВКЛИДОВА ГЕОМЕТРИЯ — ЕВКЛИДОВА ГЕОМЕТРИЯ, система геометрии, основанная на АКСИОМАХ, сформулированных в книге ЕВКЛИДА «Начала». Исходя из набора самоочевидных положений (аксиом) и пользуясь жесткой логикой, Евклид пришел к ряду важных результатов. Его выводы… … Научно-технический энциклопедический словарь

ЕВКЛИДОВА ГЕОМЕТРИЯ — (элементарная геометрия) (см.) пространства, описываемая системой аксиом и постулатов, изложенных древнегреческим математиком и астрономом Евклидом (III в. до н. э.) в его главном труде «Начала». Древние понятия и преобразования, приведенные в… … Большая политехническая энциклопедия

ЕВКЛИДОВА ГЕОМЕТРИЯ — ЕВКЛИДОВА геометрия, геометрия, описывающая простейшие свойства физического пространства. Исходными объектами евклидовой геометрии являются точки, прямые, плоскости. Основные положения евклидовой геометрии сосредоточены в системе аксиом, первая… … Современная энциклопедия

ЕВКЛИДОВА ГЕОМЕТРИЯ — геометрия, систематическое построение которой было осуществлено в Началах Евклида. Возникновение Евклидовой геометрии связано с наглядными представлениями об окружающем нас мире (напр., прямые линии натянутые нити и т. п.) Длительный процесс… … Большой Энциклопедический словарь

Евклидова геометрия — ЕВКЛИДОВА ГЕОМЕТРИЯ, геометрия, описывающая простейшие свойства физического пространства. Исходными объектами евклидовой геометрии являются точки, прямые, плоскости. Основные положения евклидовой геометрии сосредоточены в системе аксиом, первая… … Иллюстрированный энциклопедический словарь

евклидова геометрия — геометрия, систематическое построение которой было осуществлено в «Началах» Евклида. Возникновение евклидовой геометрии связано с наглядными представлениями об окружающем нас мире (например, прямые линии натянутые нити и т. п.). Длительный… … Энциклопедический словарь

Евклидова геометрия — геометрия, систематическое построение которой было впервые дано в 3 в. до н. э. Евклидом. Система аксиом Е. г. опирается на следующие основные понятия: точка, прямая, плоскость, движение и следующие отношения: «точка лежит на прямой на… … Большая советская энциклопедия

ЕВКЛИДОВА ГЕОМЕТРИЯ — геометрия, систе матич. построение к рой было осуществлено в Началах Евклида. Возникновение Е. г. связано с наглядными представлениями об окружающем нас мире (напр., прямые линии натянутые нити и т. п.). Длит. процесс углубления наших… … Естествознание. Энциклопедический словарь

Евклидова геометрия — геометрия, построенная на базе аксиом абсолютной геометрии (являющейся общей частью как евклидовой, так и геометрии Лобачевского) и знаменитой аксиомы Евклида о параллельных (через точку А, не принадлежащую прямой а, в плоскости, определяемой… … Начала современного естествознания

Источник

Евклидова геометрия

Полезное

Смотреть что такое «Евклидова геометрия» в других словарях:

ЕВКЛИДОВА ГЕОМЕТРИЯ — ЕВКЛИДОВА ГЕОМЕТРИЯ, система геометрии, основанная на АКСИОМАХ, сформулированных в книге ЕВКЛИДА «Начала». Исходя из набора самоочевидных положений (аксиом) и пользуясь жесткой логикой, Евклид пришел к ряду важных результатов. Его выводы… … Научно-технический энциклопедический словарь

ЕВКЛИДОВА ГЕОМЕТРИЯ — (элементарная геометрия) (см.) пространства, описываемая системой аксиом и постулатов, изложенных древнегреческим математиком и астрономом Евклидом (III в. до н. э.) в его главном труде «Начала». Древние понятия и преобразования, приведенные в… … Большая политехническая энциклопедия

ЕВКЛИДОВА ГЕОМЕТРИЯ — ЕВКЛИДОВА геометрия, геометрия, описывающая простейшие свойства физического пространства. Исходными объектами евклидовой геометрии являются точки, прямые, плоскости. Основные положения евклидовой геометрии сосредоточены в системе аксиом, первая… … Современная энциклопедия

ЕВКЛИДОВА ГЕОМЕТРИЯ — геометрия, систематическое построение которой было осуществлено в Началах Евклида. Возникновение Евклидовой геометрии связано с наглядными представлениями об окружающем нас мире (напр., прямые линии натянутые нити и т. п.) Длительный процесс… … Большой Энциклопедический словарь

Евклидова геометрия — ЕВКЛИДОВА ГЕОМЕТРИЯ, геометрия, описывающая простейшие свойства физического пространства. Исходными объектами евклидовой геометрии являются точки, прямые, плоскости. Основные положения евклидовой геометрии сосредоточены в системе аксиом, первая… … Иллюстрированный энциклопедический словарь

Евклидова геометрия — (или элементарная геометрия) геометрическая теория, основанная на системе аксиом, впервые изложенной в «Началах» Евклида (III век до н. э.). Содержание 1 Основные сведения 2 Аксиоматика … Википедия

евклидова геометрия — геометрия, систематическое построение которой было осуществлено в «Началах» Евклида. Возникновение евклидовой геометрии связано с наглядными представлениями об окружающем нас мире (например, прямые линии натянутые нити и т. п.). Длительный… … Энциклопедический словарь

ЕВКЛИДОВА ГЕОМЕТРИЯ — геометрия, систе матич. построение к рой было осуществлено в Началах Евклида. Возникновение Е. г. связано с наглядными представлениями об окружающем нас мире (напр., прямые линии натянутые нити и т. п.). Длит. процесс углубления наших… … Естествознание. Энциклопедический словарь

Евклидова геометрия — геометрия, построенная на базе аксиом абсолютной геометрии (являющейся общей частью как евклидовой, так и геометрии Лобачевского) и знаменитой аксиомы Евклида о параллельных (через точку А, не принадлежащую прямой а, в плоскости, определяемой… … Начала современного естествознания

Источник

233,Евклид – отец геометрии (кратко)

? Здравствуйте, друзья! В статье «Евклид: краткая биография, открытия, факты, видео» — о жизни древнегреческого математика и философа. «Евклид» — в переводе с древнегреческого языка означает «добрая слава».

Краткая биография

Биография Евклида до конца не изучена, к примеру, до сих пор неизвестен год рождения. Известно, что он появился на свет в небольшом районе Афин и был платоновским учеником.

Подъем его научной работы пришелся на правление Птолемея Первого. Некоторые сведения о его жизни можно проследить по арабским рукописям и архимедовым письмам к друзьям. Так, по ним можно определить, что Евклид был сыном греческого ученого и жил около Тира в Сирии.

С малых лет получал знания о мире от своего отца, он же привил сыну любовь к естественным наукам, а затем Евклид поступил в школу Платона, где и обучился математическим основам.

Повзрослев, его пригласили в храм Мусейон (по другим данным он был одним из его основателей), в котором собирались видные ученые с поэтами. Тут были классы для занятий. Также храм был заполнен садами с башнями астрономии, помещениями для одиноких размышлений и большой библиотекой.

В Мусейоне он смог открыть школу с лучшими математиками и монументальный труд в области математики, в котором заложил планиметрические основы со стереометрией, теорией чисел, законами алгебры, методами нахождения площадей с объемами и др.

Фрагмент папируса с текстом «Начал» Евклида

Монументальный труд — публикация «Начала». Это серия из 13 книг, представляющая собой обработанные публикации древнегреческих математиков с пятого по четвертый век до нашей эры.

Кроме «Начал», было создано еще одно сочинение — «Данные», в котором были опубликованы основы по геометрическому анализу. Кроме того, александрийский ученый создал учебник, с помощью которого в то время и сейчас изучают астрономию, перспективу, отражение в зеркале, музыкальные интервалы и решают тригонометрические задачи.

Все оставшиеся годы жизни посвятил изучению естественных наук и математических законов, отчего его называют отцом геометрии. О других аспектах его жизни неизвестно до сих пор. Умер в Александрии.

Геометрия. Раздел математики

Раздел математики именуемый словом «геометрия» восходит к греческим «Земля» (гео) и «измерение» (метри). Как следует из названия данной дисциплины, грекам было нужно измерять элементарные природные формы. Практическое значение геометрии лежит в области землемерия и картографии, математических методов определения объема, площади и длины. Кроме этого, греческие ученые скоро поняли, что всякие формы подчиняются определенным закономерностям и правилам. Около 300 г. до н. э. греческий великий математик Евклид из Александрии собрал и детально обрисовал правила геометрии в труде «Начала», складывающемся из 13 книг. В нем он представил комплект определений, аксиом, теорем и математических доказательств, ставших основой геометрии как научной дисциплины. На изложенные в «Началах» положения опираются все математические дисциплины, развившиеся из геометрии. Вклад Евклида в математику настолько велик и глубок, что его называют «отцом геометрии».

Постулаты Евклида

Его главная книга «Элементы» (первоначально написанная на древнегреческом языке) стала базовой работой важных математических учений. Она разделена на 13 отдельных книг.

Гений Евклида состоял в том, чтобы взять в оборот множество разнообразных элементов математических идей и объединить их в один логический, последовательный формат.

Лемма Евклида, которая утверждает, что фундаментальное свойство простых чисел состоит в том, что если простое число делит произведение двух чисел, оно должно делить по крайней мере одно из этих чисел.

Что такое «евклидова геометрия»?

Свои знания в планиметрии и стереометрии гениальный мыслитель формулировал в виде аксиом и постулатов. Система аксиом касалась четырёх понятий: точки, прямой, плоскости, движения, а также взаимоотношения этих понятий между собой.

Для построения конкретных фигур на плоскости или в пространстве он разработал систему постулатов, предписывающих конкретные действия. Подобная система аксиом и постулатов в современности получила название «евклидова геометрия».

Постулаты и аксиомы из трудов “Начала” Евклида

Многие теоремы, приведенные в «Началах», были сформулированы не Евклидом. Вклад Евклида заключался в том, дабы привести их к единому стандарту изложения и единому комплекту первоначальных предположений либо аксиом. В их число входят пять известных универсальных аксиом Евклида.

Универсальные аксиомы Евклида

1) величины, равные одному и тому же, равны и между собой;

2) если к равным величинам прибавляются равные, то и целые величины будут равны;

3) если от равных величин отнимаются равные, то остатки будут равны;

4) совмещающиеся (совпадающие) друг с другом величины равны между собой;

5) целое больше части.

Пять постулатов Евклида звучат более «геометрически»:

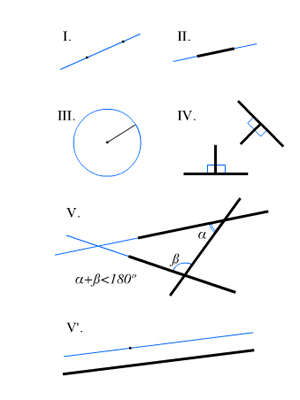
1) от всякой точки до всякой точки возможно провести участок прямой;

2) участок прямой возможно непрерывно продолжать по прямой;

3) из любой начальной точки участка прямой всяким радиусом может быть описана окружность, наряду с этим эта точка станет ее центром;

4) все прямые углы конгруэнтны (т. е. смогут быть преобразованы друг в друга);

5) если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых углов (равных 90°), то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых углов.

V постулат знаменит как постулат о параллельности. Позднее было доказано, что он недоказуем, что привело к появлению новых форм геометрии, основанных на другом комплекте аксиом.

«Начала» Евклида

Основное сочинение Евклида называется Начала. Книги с таким же названием, в которых последовательно излагались все основные факты геометрии и теоретической арифметики, составлялись ранее Гиппократом Хиосским, Леонтом и Февдием. Однако Начала Евклида вытеснили все эти сочинения из обихода и в течение более чем двух тысячелетий оставались базовым учебником геометрии. Создавая свой учебник, Евклид включил в него многое из того, что было создано его предшественниками, обработав этот материал и сведя его воедино.

Начала состоят из тринадцати книг. Первая и некоторые другие книги предваряются списком определений. Первой книге предпослан также список постулатов и аксиом. Как правило, постулаты задают базовые построения (напр., «требуется, чтобы через любые две точки можно было провести прямую»), а аксиомы — общие правила вывода при оперировании с величинами (напр., «если две величины равны третьей, они равны между собой»).

Евклид открывает врата Сада Математики. Иллюстрация из трактата Никколо Тартальи «Новая наука»

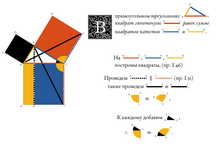
В I книге изучаются свойства треугольников и параллелограммов; эту книгу венчает знаменитая теорема Пифагора для прямоугольных треугольников. Книга II, восходящая к пифагорейцам, посвящена так называемой «геометрической алгебре». В III и IV книгах излагается геометрия окружностей, а также вписанных и описанных многоугольников; при работе над этими книгами Евклид мог воспользоваться сочинениями Гиппократа Хиосского. В V книге вводится общая теория пропорций, построенная Евдоксом Книдским, а в VI книге она прилагается к теории подобных фигур. VII—IX книги посвящены теории чисел и восходят к пифагорейцам; автором VIII книги, возможно, был Архит Тарентский. В этих книгах рассматриваются теоремы о пропорциях и геометрических прогрессиях, вводится метод для нахождения наибольшего общего делителя двух чисел (известный ныне как алгоритм Евклида), строятся чётные совершенные числа, доказывается бесконечность множества простых чисел. В X книге, представляющей собой самую объёмную и сложную часть Начал, строится классификация иррациональностей; возможно, что её автором является Теэтет Афинский. XI книга содержит основы стереометрии. В XII книге с помощью метода исчерпывания доказываются теоремы об отношениях площадей кругов, а также объёмов пирамид и конусов; автором этой книги по общему признанию является Евдокс Книдский. Наконец, XIII книга посвящена построению пяти правильных многогранников; считается, что часть построений была разработана Теэтетом Афинским.

В дошедших до нас рукописях к этим тринадцати книгам прибавлены ещё две. XIV книга принадлежит александрийцу Гипсиклу (ок. 200 г. до н. э.), а XV книга создана во время жизни Исидора Милетского, строителя храма св. Софии в Константинополе (начало VI в. н. э.).

Начала предоставляют общую основу для последующих геометрических трактатов Архимеда, Аполлония и других античных авторов; доказанные в них предложения считаются общеизвестными. к Началам в античности составляли Герон, Порфирий, Папп, Прокл, Симпликий. Сохранился комментарий Прокла к I книге, а также комментарий Паппа к X книге (в арабском переводе). От античных авторов комментаторская традиция переходит к арабам, а потом и в Средневековую Европу.

В создании и развитии науки Нового времени Начала также сыграли важную идейную роль. Они оставались образцом математического трактата, строго и систематически излагающего основные положения той или иной математической науки.

Алгоритм Евклида

Используя лемму Евклида, эта теорема утверждает, что каждое целое число больше единицы либо само по себе простое число, либо произведение простых чисел и что существует определенный порядок простых чисел.

«Если два числа, умножая одно на другое, составляют некоторое число, и любое число, которое делится на их произведение, также будет делиться на каждое из исходных чисел».

Евклидов алгоритм — эффективный метод вычисления наибольшего общего делителя (НОД) двух чисел, наибольшего числа, которое делит их оба, не оставляя остатка.

Достижения Евклида

Основная масса трудов учёного была написана по математике:

Известны труды учёного по смежным дисциплинам – музыке, астрономии, оптике:

Арабские учёные считают этого математика автором некоторых работ по механике и определению удельного веса тел.

В этом видео дополнительная и интересная информация к статье «Евклид: краткая биография, открытия, факты, видео»

? Друзья, если вам понравилась статья «Евклид: краткая биография, открытия, факты», поделитесь в социальных сетях.

Евклид и античная философия

Уже со времён пифагорейцев и Платона арифметика, музыка, геометрия и астрономия (так называемые «математические» науки; позже Боэцием названные квадривием) рассматривались в качестве образца систематического мышления и предварительной ступени для изучения философии. Не случайно возникло предание, согласно которому над входом в платоновскую Академию была помещена надпись «Да не войдёт сюда не знающий геометрии».

Геометрические чертежи, на которых при проведении вспомогательных линий неявная истина становится очевидной, служат иллюстрацией для учения о припоминании, развитого Платоном в Меноне и других диалогах. Предложения геометрии потому и называются теоремами, что для постижения их истины требуется воспринимать чертёж не простым чувственным зрением, но «очами разума». Всякий же чертёж к теореме представляет собой идею: мы видим перед собой эту фигуру, а ведём рассуждения и делаем заключения сразу для всех фигур одного с ней вида.

Некоторый «платонизм» Евклида связан также с тем, что в Тимее Платона рассматривается учение о четырёх элементах, которым соответствуют четыре правильных многогранника (тетраэдр — огонь, октаэдр — воздух, икосаэдр — вода, куб — земля), пятый же многогранник, додекаэдр, «достался в удел фигуре вселенной». В связи с этим Начала могут рассматриваться как развёрнутое со всеми необходимыми посылками и связками учение о построении пяти правильных многогранников — так называемых «платоновых тел», завершающееся доказательством того факта, что других правильных тел, кроме этих пяти, не существует.

Для аристотелевского учения о доказательстве, развитого во Второй аналитике, Начала также предоставляют богатый материал. Геометрия в Началах строится как выводная система знаний, в которой все предложения последовательно выводятся одно за другим по цепочке, опирающейся на небольшой набор начальных утверждений, принятых без доказательства. Согласно Аристотелю, такие начальные утверждения должны иметься, так как цепочка вывода должна где-то начинаться, чтобы не быть бесконечной. Далее, Евклид старается доказывать утверждения общего характера, что тоже соответствует любимому примеру Аристотеля: «если всякому равнобедренному треугольнику присуще иметь углы, в сумме равные двум прямым, то это присуще ему не потому что он равнобедренный, а потому что он треугольник» (An. Post. 85b12).

Геометрия и компьютерная графика

Компьютерная анимация (CGI) преображает сложные природные формы (такие, как лицо) в комплект несложных форм. Так, сложный объект создаётся за счет комбинации несложных объектов и может изменяться в следствии трансформации их геометрии. В базе данной идеи — изучения математиков, например, французско-американского ученого Бенуа Мандельброта, который в 1974 г. продемонстрировал, что естественные формы подчиняются правилам фрактальной размерности (неэвклидова геометрия), а в рамках классической евклидовой геометрии смогут быть измерены только примерно.

Компьютерная графика на основе фракталов Мандельброта

О том как знание математики позволяет заработать на майнинге криптовалюты.

Tags: «Начала» Евклида геометрия история математики

Псевдо-Евклид

Евклиду приписываются два важных трактата об античной теории музыки: «Гармоническое введение» («Гармоника») и «Деление канона» (лат. Sectio canonis). Традиция приписывать «Деление канона» Евклиду идёт ещё от Порфирия. В старинных рукописях «Гармоники» авторство приписывается Евклиду, некоему Клеониду, а также александрийскому математику Паппу. Генрих Мейбомrude (1555—1625) снабдил «Гармоническое введение» обстоятельными примечаниями, и вместе с «Делением канона» приписал их к трудам Евклида.

При последующем подробном анализе этих трактатов было определено, что первый написан в аристоксеновской традиции (например, в нём все полутоны считаются равными), а второй по стилю — явно пифагорейский (например, отрицается возможность деления тона ровно пополам). Стиль изложения «Гармонического введения» отличается догматизмом и непрерывностью, стиль «Деления канона» несколько схож с «Началами» Евклида, поскольку содержит теоремы и доказательства.

После критической публикации «Гармоники» знаменитым немецким филологом Карлом Яном (1836—1899) этот трактат стали повсеместно приписывать Клеониду и датировать II в. н.э. В русском переводе (с комментариями) его впервые издал Г. А. Иванов (Москве, 1894). «Деление канона» ныне одна часть исследователей считает аутентичным сочинением Евклида, а другая — анонимным сочинением в традициях Евклида. Последние по времени русские переводы «Деления канона» опубликованы (в версии Порфирия) В.Г.Цыпиным и (в версии Боэция) С.Н.Лебедевым. Критическое издание оригинального текста «Деления канона» выполнил в 1991 г. А.Барбера.

Достижения Евклида

Достижения Евклида имели огромное значение для мировой истории, математики и других наук.

Он был первым, кто:

Математика

Евклид — отец математики. Он сформулировал теоремы по планиметрии, упростил понимание теоремы Пифагора и теоремы о сумме углов треугольника, прописал свойства правильных многоугольников и законы построения правильных пятнадцатиугольников, указал, как применима алгебры в жизни и каковы ее основные теории, вписал теорию о целом и рациональном числе, рассмотрел квадратичную иррациональность, заложил основы стереометрической науки, доказал теоремы, касающиеся площади круга с объемом шара, вывел отношение объема пирамид с конусами, призмами и цилиндрами.

Другие науки

Помимо математики, ученый работал с оптикой, астрономией, логикой и музыкой. Так, в оптике он дал сведения об оптической перспективе, зеркальных искажениях и отражениях световых лучей в зеркале.

Тексты и переводы

Старые русские переводы

Средневековые армянские переводы

В XI веке н.э. Григор Магистрос перевел с греческого на армянский «Начала» Евклида. Более обширный перевод Евклида сделан в позднем средневековье и приписывается автору XVII века Григору Кесараци.

Современные издания сочинений Евклида

Интересные факты из жизни

Несколько любопытных фактов из биографии Евклида:

В целом, Евклид является отцом геометрии, и он не случайно так называется. Он первым сделал сложное понятным и дал толчок развитию естественных наук. Его книги неоценимы по значимости и применяются сегодня в области математических и геометрических наук во всем мире.

Литература

Фрагмент из русского перевода «Начал Евлкида» Бирна.

Источник