За счет чего происходит дискретизация по времени

Цифровое представление аналогового аудиосигнала. Краткий ликбез

Дорогие читатели, меня зовут Феликс Арутюнян. Я студент, профессиональный скрипач. В этой статье хочу поделиться с Вами отрывком из моей презентации, которую я представил в университете музыки и театра Граца по предмету прикладная акустика.

Рассмотрим теоретические аспекты преобразования аналогового (аудио) сигнала в цифровой.
Статья не будет всеохватывающей, но в тексте будут гиперссылки для дальнейшего изучения темы.

Чем отличается цифровой аудиосигнал от аналогового?

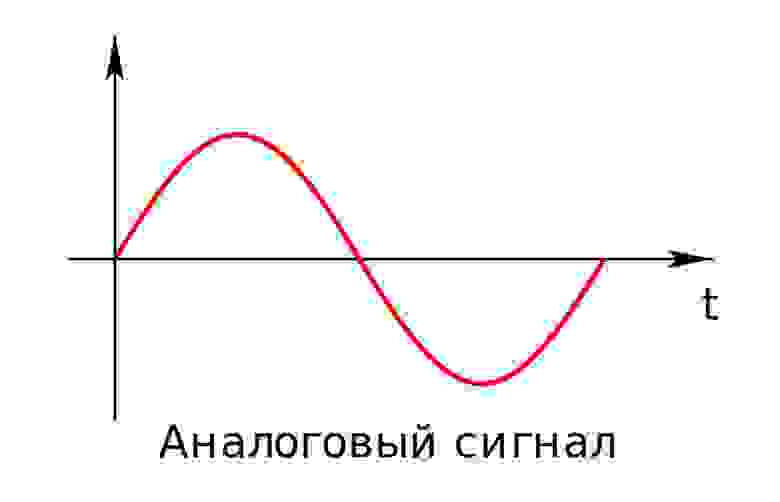
Аналоговый (или континуальный) сигнал описывается непрерывной функцией времени, т.е. имеет непрерывную линию с непрерывным множеством возможных значений (рис. 1).

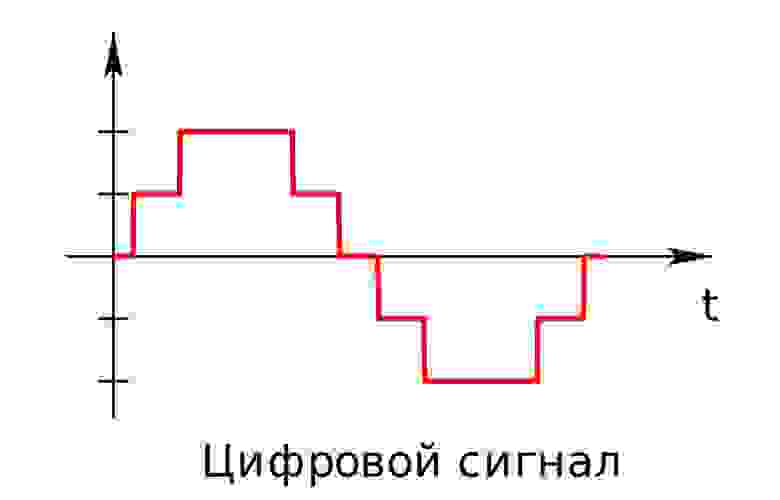
Цифровой сигнал — это сигнал, который можно представить как последовательность определенных цифровых значений. В любой момент времени он может принимать только одно определенное конечное значение (рис. 2).

Аналоговый сигнал в динамическом диапазоне может принимать любые значения. Аналоговый сигнал преобразуется в цифровой с помощью двух процессов — дискретизация и квантование. Очередь процессов не важна.

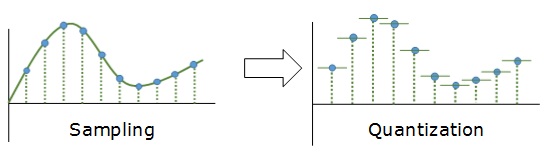
Дискретизацией называется процесс регистрации (измерения) значения сигнала через определенные промежутки (обычно равные) времени (рис. 3).

Квантование — это процесс разбиения диапазона амплитуды сигнала на определенное количество уровней и округление значений, измеренных во время дискретизации, до ближайшего уровня (рис. 4).

Дискретизация разбивает сигнал по временной составляющей (по вертикали, рис. 5, слева).
Квантование приводит сигнал к заданным значениям, то есть округляет сигнал до ближайших к нему уровней (по горизонтали, рис. 5, справа).

Эти два процесса создают как бы координатную систему, которая позволяет описывать аудиосигнал определенным значением в любой момент времени.
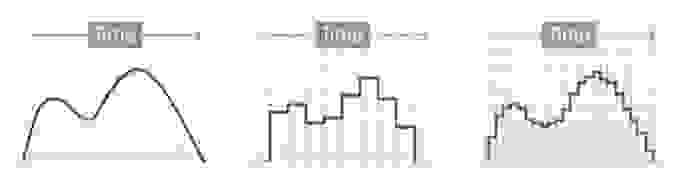
Цифровым называется сигнал, к которому применены дискретизация и квантование. Оцифровка происходит в аналого-цифровом преобразователе (АЦП). Чем больше число уровней квантования и чем выше частота дискретизации, тем точнее цифровой сигнал соответствует аналоговому (рис. 6).

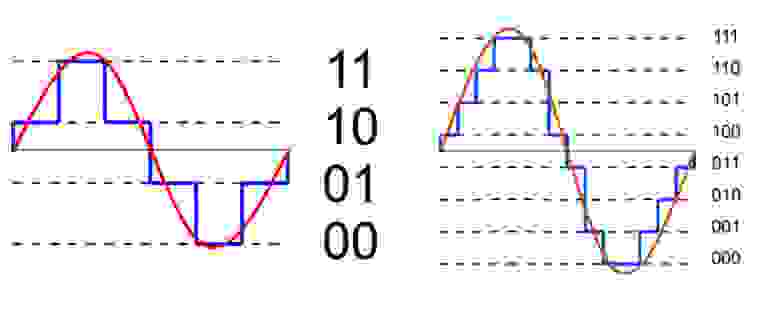
Уровни квантования нумеруются и каждому уровню присваивается двоичный код. (рис. 7)

Количество битов, которые присваиваются каждому уровню квантования называют разрядностью или глубиной квантования (eng. bit depth). Чем выше разрядность, тем больше уровней можно представить двоичным кодом (рис. 8).

Данная формула позволяет вычислить количество уровней квантования:

Если N — количество уровней квантования,
n — разрядность, то

Обычно используют разрядности в 8, 12, 16 и 24 бит. Несложно вычислить, что при n=24 количество уровней N = 16,777,216.

При n = 1 аудиосигнал превратится в азбуку Морзе: либо есть «стук», либо нету. Существует также разрядность 32 бит с плавающей запятой. Обычный компактный Аудио-CD имеет разрядность 16 бит. Чем ниже разрядность, тем больше округляются значения и тем больше ошибка квантования.

Ошибкой квантований называют отклонение квантованного сигнала от аналогового, т.е. разница между входным значением и квантованным значением ()

Большие ошибки квантования приводят к сильным искажениям аудиосигнала (шум квантования).

Чем выше разрядность, тем незначительнее ошибки квантования и тем лучше отношение сигнал/шум (Signal-to-noise ratio, SNR), и наоборот: при низкой разрядности вырастает шум (рис. 9).

Разрядность также определяет динамический диапазон сигнала, то есть соотношение максимального и минимального значений. С каждым битом динамический диапазон вырастает примерно на 6dB (Децибел) (6dB это в 2 раза; то есть координатная сетка становиться плотнее, возрастает градация).

Ошибки квантования (округления) из-за недостаточного количество уровней не могут быть исправлены.

50dB SNR
примечание: если аудиофайлы не воспроизводятся онлайн, пожалуйста, скачивайте их.

Теперь о дискретизации.

Как уже говорили ранее, это разбиение сигнала по вертикали и измерение величины значения через определенный промежуток времени. Этот промежуток называется периодом дискретизации или интервалом выборок. Частотой выборок, или частотой дискретизации (всеми известный sample rate) называется величина, обратная периоду дискретизации и измеряется в герцах. Если
T — период дискретизации,
F — частота дискретизации, то

Чтобы аналоговый сигнал можно было преобразовать обратно из цифрового сигнала (точно реконструировать непрерывную и плавную функцию из дискретных, «точечных» значении), нужно следовать теореме Котельникова (теорема Найквиста — Шеннона).

Теорема Котельникова гласит:

Если аналоговый сигнал имеет финитный (ограниченной по ширине) спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчетам, взятым с частотой, строго большей удвоенной верхней частоты.

Вам знакомо число 44.1kHz? Это один из стандартов частоты дискретизации, и это число выбрали именно потому, что человеческое ухо слышит только сигналы до 20kHz. Число 44.1 более чем в два раза больше чем 20, поэтому все частоты в цифровом сигнале, доступные человеческому уху, могут быть преобразованы в аналоговом виде без искажении.

Но ведь 20*2=40, почему 44.1? Все дело в совместимости с стандартами PAL и NTSC. Но сегодня не будем рассматривать этот момент. Что будет, если не следовать теореме Котельникова?

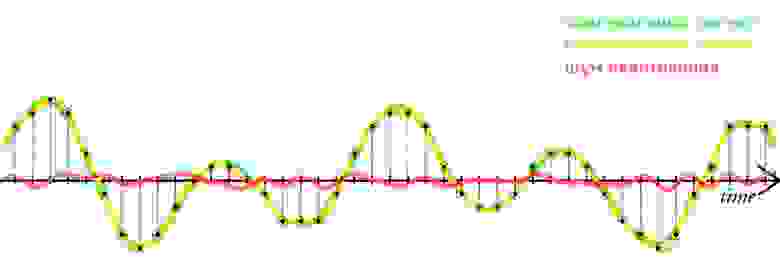
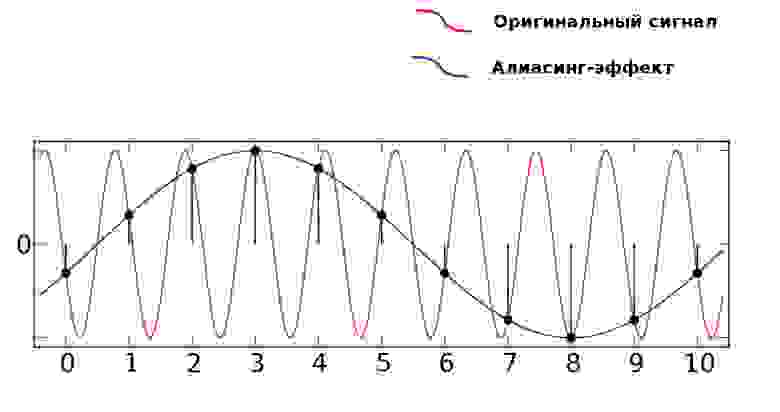
Когда в аудиосигнале встречается частота, которая выше чем 1/2 частоты дискретизации, тогда возникает алиасинг — эффект, приводящий к наложению, неразличимости различных непрерывных сигналов при их дискретизации.

Как видно из предыдущей картинки, точки дискретизации расположены так далеко друг от друга, что при интерполировании (т.е. преобразовании дискретных точек обратно в аналоговый сигнал) по ошибке восстанавливается совершенно другая частота.

Аудиопример 4: Линейно возрастающая частота от

100 до 8000Hz. Частота дискретизации — 16000Hz. Нет алиасинга.

Аудиопример 5: Тот же файл. Частота дискретизации — 8000Hz. Присутствует алиасинг

Пример:
Имеется аудиоматериал, где пиковая частота — 2500Hz. Значит, частоту дискретизации нужно выбрать как минимум 5000Hz.

Следующая характеристика цифрового аудио это битрейт. Битрейт (bitrate) — это объем данных, передаваемых в единицу времени. Битрейт обычно измеряют в битах в секунду (Bit/s или bps). Битрейт может быть переменным, постоянным или усреднённым.

Следующая формула позволяет вычислить битрейт (действительна только для несжатых потоков данных):

Битрейт = Частота дискретизации * Разрядность * Количество каналов

Например, битрейт Audio-CD можно рассчитать так:
44100 (частота дискретизации) * 16 (разрядность) * 2 (количество каналов, stereo)= 1411200 bps = 1411.2 kbit/s

При постоянном битрейте (constant bitrate, CBR) передача объема потока данных в единицу времени не изменяется на протяжении всей передачи. Главное преимущество — возможность довольно точно предсказать размер конечного файла. Из минусов — не оптимальное соотношение размер/качество, так как «плотность» аудиоматериала в течении музыкального произведения динамично изменяется.

При кодировании переменным битрейтом (VBR), кодек выбирает битрейт исходя из задаваемого желаемого качества. Как видно из названия, битрейт варьируется в течение кодируемого аудиофайла. Данный метод даёт наилучшее соотношение качество/размер выходного файла. Из минусов: точный размер конечного файла очень плохо предсказуем.

Усреднённый битрейт (ABR) является частным случаем VBR и занимает промежуточное место между постоянным и переменным битрейтом. Конкретный битрейт задаётся пользователем. Программа все же варьирует его в определенном диапазоне, но не выходит за заданную среднюю величину.

При заданном битрейте качество VBR обычно выше чем ABR. Качество ABR в свою очередь выше чем CBR: VBR > ABR > CBR.

ABR подходит для пользователей, которым нужны преимущества кодирования VBR, но с относительно предсказуемым размером файла. Для ABR обычно требуется кодирование в 2 прохода, так как на первом проходе кодек не знает какие части аудиоматериала должны кодироваться с максимальным битрейтом.

Существуют 3 метода хранения цифрового аудиоматериала:

Несжатый (RAW) формат данных

Другой формат хранения несжатого аудиопотока это WAV. В отличие от RAW, WAV содержит заголовок файла.

Аудиоформаты с сжатием без потерь

Принцип сжатия схож с архиваторами (Winrar, Winzip и т.д.). Данные могут быть сжаты и снова распакованы любое количество раз без потери информации.

Как доказать, что при сжатии без потерь, информация действительно остаётся не тронутой? Это можно доказать методом деструктивной интерференции. Берем две аудиодорожки. В первой дорожке импортируем оригинальный, несжатый wav файл. Во второй дорожке импортируем тот же аудиофайл, сжатый без потерь. Инвертируем фазу одного из дорожек (зеркальное отображение). При проигрывании одновременно обеих дорожек выходной сигнал будет тишиной.

Это доказывает, что оба файла содержат абсолютно идентичные информации (рис. 11).

Кодеки сжатия без потерь: flac, WavPack, Monkey’s Audio…

При сжатии с потерями

акцент делается не на избежание потерь информации, а на спекуляцию с субъективными восприятиями (Психоакустика). Например, ухо взрослого человек обычно не воспринимает частоты выше 16kHz. Используя этот факт, кодек сжатия с потерями может просто жестко срезать все частоты выше 16kHz, так как «все равно никто не услышит разницу».

Другой пример — эффект маскировки. Слабые амплитуды, которые перекрываются сильными амплитудами, могут быть воспроизведены с меньшим качеством. При громких низких частотах тихие средние частоты не улавливаются ухом. Например, если присутствует звук в 1kHz с уровнем громкости в 80dB, то 2kHz-звук с громкостью 40dB больше не слышим.

Этим и пользуется кодек: 2kHz-звук можно убрать.

Кодеки сжатия с потерям: mp3, aac, ogg, wma, Musepack…

Источник

Дискретизация по времени

Дискретизация по времени

Аналоговый сигнал, являющийся исходным материалом для АЦП (аналогово-цифровой преобразователь), представляет собой непрерывный сигнал, описывающий изменения амплитуды и частоты звукового давления в течении времени. Чтобы преобразовать аналогововый сигнал в цифровую форму, необходимо произвести его дискретизацию, т.е. разбить на отдельные (дискретные) элементы, как по амплитуде, так и по времени.

Ответственность за дискретизацию по времени берет на себя тактовый генератор, определяющий периодичность, с которой производятся дискретные замеры. Эту периодичность называют частотой дискретизации, которая определяет частоту (количество) производимых замеров в секунду и измеряется в Герцах (Hz), а точнее в тысячах Герц (KHz). Замеры должны производится в определенные и точные моменты времени, отклонение от которых вызывает эффект известный под названием джиттер.

Шагом дискретизации называют время между замерами. Шаг всегда будет составлять 1/частоту дискретизации. Например, стандартная частота дискретизации аудио на CD составляет 44.1 KHz. Это означает, что замер мгновенных значений амплитуды производится 44,100 раз в секунду, а шаг дискретизации при этом равен 1 ÷ 44.100 = 0.022 миллисекунды. Другими словами, замер амплитуды производится каждые 0.022 миллисекунды. На первый взгляд это кажется невероятно быстро, но если учесть, что при частоте 20 KHz акустическая волна изменяет свою полярность 40.000 раз в секунду, то становится понятно, что такая частота дискретизации является абсолютной необходимостью.

В результате дискретизации по амплитуде, каждое замерянное значение регистрируется в виде ряда (слова) нулей и единиц в соответствии с постулатами бинарной системы. Это означает, что в одной секунде цифрового аудио CD качества записаны 44,100 таких слов, характеризующих значение амплитуды исходного аналогового сигнала во время каждого дискретного (отдельного) замера.

Например, если провести преобразование постоянного тока (DC) в цифровую форму, то все измерянные и зарегистрированные значения будут абсолютно идентичны, так как от самого первого и до самого последнего измерения никаких изменений амплитуды не происходило.

Однако со звуком дела обстоят иначе. Даже самая низкая частота, воспринимаемая человеческим слухом (20 Hz), меняет полярность 40 раз в секунду (в каждом цикле происходит изменение полярности – положительная и отрицательная фазы). Наивысшая же частота, доступная восприятию нашего слухового аппарата, изменяет полярность 40.000 раз в секунду. Отсюда можно сделать вывод, что для того, чтобы корректно передать всю частотную информацию, содержащуюся в сигнале, необходимо произвести замер значения амплитуды как минимум один раз в каждой его фазе, то есть как минимум 40.000 раз, если исходить из предположения, что в сигнале содержатся частоты до 20 KHz. Иначе возникает эффект Aliasing, который вносит сущственные искажения в оцифрованный аудио сигнал. Чтобы этого избежать необходимо соблюсти несколько правил. Это подводит нас к теореме Котельникова (известна также как теорема Найквиста).

Стоит добавить, что наиболее распространнеными являются следующие частоты дискретизации: 44.1 KHz, 48 KHz, 88.2 KHz, 96 KHz и 192 KHz. Чем выше частота дискретизации, тем более детально будет представлен исходный сигнал, однако будет требовать больших рессурсов процессора, при последующей обработке. Это объясняется тем, что за ту же единицу времени будет необходимо обсчитывать большее количество информации. Если при частоте 44.1 KHz в секундном отрезке записано 44100 дискретных значений амплитуды, то при частоте 192 KHz, на том же отрезке в секунду будет записано 192000 дискретных значений. Разница на лицо! Не стоит забывать и о том, что при использовании высоких частот дискретизаци растет и объем ъолученного файла. Так, например, если при 44.1 KHz/ 16 bit одна минута моно сигнала будет иметь объем около 5 Mb, то при 88.2 KHz, ровно в два раза больше, то есть около 10 Mb.

Источник

Квантование аналогового сигнала по времени

На рисунке 1 приведены основные требования к устройствам дискретизации аналогового сигнала. Дискретизация непрерывных аналоговых данных должна осуществляться с интервалом времени t_д = 1/f_д. При разработке цифрового устройства этот период должен тщательно выбираться для реализации точного представления первоначального аналогового сигнала в цифровой форме.

КРИТЕРИИ ДИСКРЕТИЗАЦИИ ПО КОТЕЛЬНИКОВУ

Рисунок 1 Критерии неискажающей дискретизации аналогового сигнала.

Очевидно, что чем больше будет взято отсчетов аналогового сигнала на интервале времени (больше выбранная частота дискретизации), тем более точным будет представление этого сигнала в цифровом виде. При уменьшении количества отсчетов в единицу времени (уменьшении частоты дискретизации) можно достигнуть предела, после которого преобразованный в цифровую форму сигнал будет искажен до такой степени, что будет невозможно восстановить его в первоначальном виде.

Иными словами, в соответствии с теоремой Котельникова требуется, чтобы частота дискретизации аналогового сигнала была, по крайней мере, вдвое больше полосы полезного сигнала, иначе информация об исходном виде аналогового сигнала будет потеряна. Если выбрать частоту дискретизации меньше (а в большинстве практических устройства и равной) удвоенной полосы частот преобразуемого аналогового сигнала, то возникает эффект, известный как наложение (заворот) спектра (aliasing).

Обычно анализ аналоговых цепей производится при помощи синусоидального сигнала. На нем проще понять физический смысл явлений, возникающих в исследуемом блоке. Так как дискретизатор является аналоговым устройством, то воспользуемся этим методом и мы. Для понимания физического смысла наложения спектра, рассмотрим эффекты, возникающие при дискретизации синусоидального сигнала. Эти эффекты мы проанализируем, как во временном, так и в частотном представлении исследуемого сигнала.

В качестве примера, иллюстрирующего эффект наложения спектра (заворота спектра), на рисунке 2 приведена временная диаграмма синусоидального сигнала, дискретизированного по времени идеальным дискретизатором.

Рисунок 2. Влияние стробоскопического эффекта во временной области, приводящее к наложению спектров входного сигнала.

В приведенном на этом рисунке примере, частота дискретизации f_д выбрана лишь ненамного выше частоты входного аналогового сигнала f_в. То есть мы нарушили теорему Котельникова! Обратите внимание, что в результате дискретизации, мы получили отсчеты сигнала, частота которого равна разности частот дискретизации и исходного сигнала f_д – f_a. То есть мы наблюдаем низкочастотный образ реального сигнала. Этот эффект известен в технике как стробоскопический эффект.

На рисунке 3 приведено частотное представление той же самой ситуации. На этом рисунке четко видно, что на выходе идеального дискретизатора появляется не только низкочастотная составляющая с частотой f_д – f_a, но и f_д + f_a, 2×f_д – f_a, 2×f_д + f_a и т.д.

Рисунок 3. Спектр дискретизированного аналогового сигнала

Полоса сигнала по Котельникову определяется как спектр от постоянного тока до f_д/2. Частотный спектр на входе дискретизатора разделяется на бесконечное число зон. Полоса частот каждой зоны составляет 0,5f_д. На практике, идеальный дискретизатор перемещает все высокочастотные образы сигнала в полосу частот от 0 до f_д/2, и накладывает их на сигнал, присутствующий в первой зоне частот Котельникова.

Теперь рассмотрим случай, когда частота полезного сигнала выходит за пределы первой зоны Котельникова. При частоте сигнала, немного ниже частоты дискретизации, временная диаграмма приведена на рисунке 2. Этот случай тоже можно проиллюстрировать рисунком 3, однако на этот раз в качестве входного сигнала следует рассматривать сигнал во второй зоне Котельникова, а компонента сигнала в первой зоне возникает после процесса дискретизации.

Обратите внимание, что, несмотря на то, что сигнал находится вне первой зоны Найквиста, его продукт преобразования f_д – f_a попадает внутрь этой зоны. Возвращаясь к рисунку 3, становится ясно, что, если мешающий сигнал появляется на любом из образов частоты f_a, то он тут же переносится на частоту f_a, приводя, таким образом, к появлению мешающего частотного компонента в первой зоне Котельникова.

Такой процесс подобен работе аналогового смесителя. Это означает, что перед устройством дискретизации сигнала обязательно требуется аналоговая фильтрация, подавляющая компоненты этого сигнала, частоты которых находятся вне полосы первой зоны Котельникова и после дискретизации попадают в ее пределы. Требования к амплитудно-частотной характеристике аналогового фильтра на входе дискретизатора будут зависеть от того, как близко частота внеполосного сигнала отстоит от f_д/2, а также величиной требуемого подавления. Эти вопросы мы рассмотрим позднее в главе, посвященной фильтрам, предназначенным для устранения эффекта наложения спектров.

Понравился материал? Поделись с друзьями!

Вместе со статьей «Квантование (дискретизация) аналогового сигнала по времени» читают:

Источник

За счет чего происходит дискретизация по времени

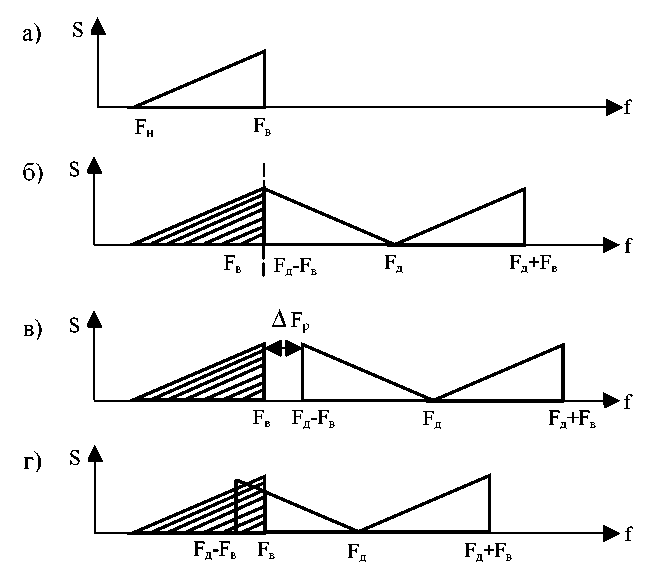
оБ ТЙУ. 24 РПЛБЪБО РТЙНЕТ ТБУЮЕФБ УРЕЛФТБМШОПК РМПФОПУФЙ. еУМЙ Ч УРЕЛФТЕ ЙНЕАФУС ЮБУФПФЩ F_n$»> (ТЙУ. 24, Б ), ФП ЗТБЖЙЛ ЙУФЙООПК УРЕЛФТБМШОПК РМПФОПУФЙ ВХДЕФ ЙУЛБЦЕО ЧУМЕДУФЧЙЕ УЧЕТФЩЧБОЙС ЮБУФПФ (ТЙУ. 24, В ).

: тЙУ. 24. уРЕЛФТБМШОБС РМПФОПУФШ РТПГЕУУБ ( Б ) Й УРЕЛФТБМШОБС РМПФОПУФШ ЬФПЗП ЦЕ РТПГЕУУБ, ЧЩЮЙУМЕООБС РП ДЙУЛТЕФОПНХ ЧТЕНЕООПНХ ТСДХ У ЮБУФПФПК ДЙУЛТЕФЙЪБГЙЙ ( В ).

ЪДЕУШ INT ПЪОБЮБЕФ ПЛТХЗМЕОЙЕ ДП ГЕМПК ЮБУФЙ ЮЙУМБ. пЫЙВЛБ ЛЧБОФПЧБОЙС ТБЧОБ

оБ РТБЛФЙЛЕ ПЫЙВЛБ ЛЧБОФПЧБОЙС ОБНОПЗП НЕОШЫЕ ДТХЗЙИ ПЫЙВПЛ, ЧПЪОЙЛБАЭЙИ Ч РТПГЕУУЕ УВПТБ Й ПВТБВПФЛЙ ДБООЩИ. пДОБЛП, ЕУМЙ ОЕРТЕТЩЧОЩК ЧИПДОПК УЙЗОБМ ЪБОЙНБЕФ НБМХА ДПМА ЫЛБМЩ ЛЧБОФПЧБОЙС, ФП ПЫЙВЛБ ЛЧБОФПЧБОЙС ВХДЕФ УХЭЕУФЧЕООПК. рПЬФПНХ ЧУЕЗДБ УМЕДХЕФ УФТЕНЙФШУС Л ФПНХ, ЮФПВЩ ДЙБРБЪПО ЙЪНЕОЕОЙС ЪОБЮЕОЙК ОЕРТЕТЩЧОПЗП РТПГЕУУБ ЪБОЙНБМ ЛБЛ НПЦОП ВПМШЫХА ЮБУФШ ЫЛБМЩ ЛЧБОФПЧБОЙС.

рПНЙНП ТБУУНПФТЕООЩИ ПЫЙВПЛ ДЙУЛТЕФЙЪБГЙЙ Й ЛЧБОФПЧБОЙС ХЛБЦЕН ДТХЗЙЕ ОБЙВПМЕЕ УХЭЕУФЧЕООЩЕ ПЫЙВЛЙ, ЛПФПТЩЕ НПЗХФ ЧПЪОЙЛБФШ Ч бгр:

— БРЕТФХТОБС ПЫЙВЛБ, ЧПЪОЙЛБАЭБС ЙЪ-ЪБ ФПЗП, ЮФП ЛБЦДЩК ПФУЮЕФ ЧЩРПМОСЕФУС ОБ РТПФСЦЕОЙЙ ОЕЛПФПТПЗП ПФТЕЪЛБ ЧТЕНЕОЙ, Б ОЕ НЗОПЧЕООП;

— ДТЕВЕЪЦБОЙЕ, СЧМСАЭЕЕУС УМЕДУФЧЙЕН ФПЗП, ЮФП ЙОФЕТЧБМ ЧТЕНЕОЙ НЕЦДХ УПУЕДОЙНЙ ПФУЮЕФБНЙ НПЦЕФ НЕОСФШУС УМХЮБКОЩН ПВТБЪПН;

— ОЕМЙОЕКОЩЕ ЙУЛБЦЕОЙС, ЛПФПТЩЕ НПЗХФ ЧПЪОЙЛБФШ РП ТБЪОЩН РТЙЮЙОБН, ОБРТЙНЕТ, ЧУМЕДУФЧЙЕ РМПИПК РПДЗПОЛЙ ДЕФБМЕК УЙУФЕНЩ ЙМЙ ОЕФПЮОПК ЗТБДХЙТПЧЛЙ;

— РТЙ ПДОПЧТЕНЕООПН РТЕПВТБЪПЧБОЙЙ Ч ОЕУЛПМШЛЙИ ЛБОБМБИ ОБМЙЮЙЕ ЙОФЕТЧБМБ ЧТЕНЕОЙ НЕЦДХ УПУЕДОЙНЙ ПРТПУБНЙ Ч ТБЪМЙЮОЩИ ЛБОБМБИ РТЙЧПДЙФ Л РПСЧМЕОЙА НЕЦЛБОБМШОПК ЧТЕНЕОО К ПЫЙВЛЙ Ч ПФУЮЕФБИ, ЛПФПТБС НПЦЕФ ПЛБЪБФШУС УХЭЕУФЧЕООПК ДМС ВЩУФТП НЕОСАЭЙИУС УЙЗОБМПЧ. рПСЧМЕОЙС ЬФПК ПЫЙВЛЙ НПЦОП ЙЪВЕЦБФШ, ЕУМЙ ЙУРПМШЪПЧБФШ Ч бгр ЪБРПНЙОБАЭЙЕ УИЕНЩ, Ч ЛПФПТЩЕ ДБООЩЕ ЙЪ ЧУЕИ ЛБОБМПЧ РПУФХРБАФ ПДОПЧТЕНЕООП Й ИТБОСФУС ФБН ДП НПНЕОФБ ПРТПУБ УППФЧЕФУФЧХАЭЕЗП ЛБОБМБ ЛПННХОЙЛБФПТПН.

Источник

Дискретизация сигнала во времени

В системе передачис временнымразделением каналов (ВРК) исходный непрерывный сигнал каждого канала подвергается преобразованного в последовательность коротких импульсов, закон изменения амплитуды которых соответствует исходному сигналу. Такой процесс можно представить модуляцией, исходным сигналом, импульсной несущей. Устройство обеспечивающее такое преобразование, называются амплитудно–импульсными модуляторами.

В промежутках между импульсами одного канала размещаются импульсы др. каналов.

В процессе формирования АИМ сигнала осуществляется дискретизация непрерывного (аналогового) сигнала во времени в соответствии с теоремой дискретизации (теоремой В.А.Котельникова): любой непрерывный сигнал, ограниченный по спектру верхней частотой Fв полностью определяется последовательностью своих дискретных отсчетов, взятых через промежуток времени Т_д=1/2 Fв, называемый периодом дискретизации. В соответствии с ним частота дискретизации, т.е. следования дискретных отсчетов, выбирается из условия Fд > 2Fв. Поскольку все реально существующие непрерывные сигналы связи представляют собой случайные процессы с бесконечно широким спектром, причем основная энергия со­средоточена в относительно узкой полосе частот, перед дискретизацией необходимо с помощью фильтра нижних частот ограничить спектр сигнала некоторой частотой Fb- Для телефонных сигналов необходимо использовать ФНЧ с частотой среза Fb=3,4 кГц. Поэтому частота дискретизации для телефонных сигналов выбрана 8 кГц.

Виды АИМ модуляции.

Различают сигналы АИМ 1-го и 2-го рода. АИМ сигнал 1-го рода является результатом дискретизации непрерывного сигнала на интервалах Котельникова. При этом вершина каждого импульса меняется в соответствии с изменением мгновенного значения сигнала.

Такой сигнал не может быть использован для последующего кодирования, т.к. изменения амплитуды импульса в процессе кодирования исказит кодовую комбинацию. Для этого отсчетное значение импульса на интервале кодирования остается неизменным. Такой сигнал называется сигналом АИМ-2 рода.

Для получения этого сигнала достаточно запомнить мгновенное значение импульса в начале отсчета и удерживать его в памяти в течение всего времени t_u.

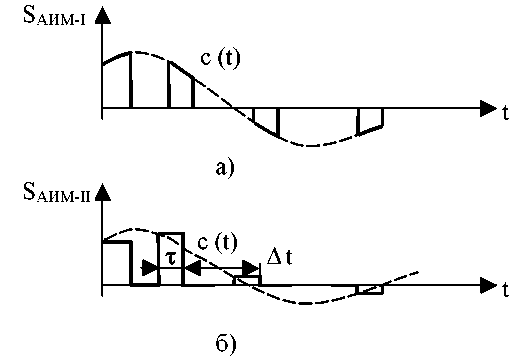
На рисунке 3.2 представлены сигналы АИМ1 и АИМ 2 рода.

Рисунок 3.2. К пояснению принципов формирования АИМ-I и АИМ-II

Различие между сигналами АИМ-I и АИМ-II оказывается существенным, если длительность импульсов τ сравнима с периодом их следования Т.

Поскольку все реально существующие непрерывные сигналы связи представляют собой случайные процессы с бесконечно широким спектром, причем основная энергия сосредоточена в относительно узкой полосе частот, перед дискретизацией на передаче необходимо с помощью фильтра нижних частот ограничить спектр канала некоторой частотой F_в. Для ТФ сигналов необходимо использовать ФНЧ с частотой среза F_в= 3,4кГц.

Рисунок 3.3. Влияние частоты дискретизации на возможность восстановления сигнала с помощью фильтра

Рис.3.4. Принципы равномерного (а) и неравномерного квантования (б)

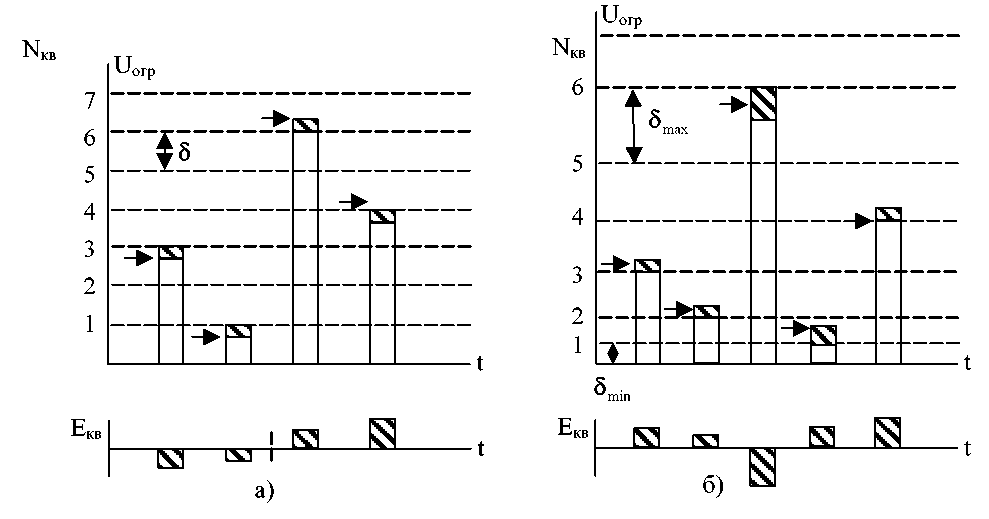
Рисунок 3.5. Амплитудные характеристики квантующих устройств

Характеристика квантования (рис.3.5) имеет две зоны: квантования при |U_вх| |U_огр|. Зона квантования является рабочей областью характеристики. В ее пределах осуществляется квантование сигнала. Чтобы не возникали шумы ограничения, применяют специальные меры, предотвращающие перегрузку квантования, т.к. возникающие шумы ограничения имеют мощность значительно превышают мощность шумов квантования.

Основной недостаток равномерного квантования заключается в следующем. Поскольку мощность шумов квантования не зависит от величины сигнала, защищенность от шумов квантования, определяемая как А₃= 10lgP/Pоказывается небольшой для сигналов с малыми уровнями (слабых сигналов) и возрастает при увеличении уровня сигнала (рис.3.4). Для того чтобы выполнить требование к защищенности А_3кв, необходимо уменьшить шаг квантования, т.е. увеличить число разрешенных уровней. При уменьшении ∆в 2 раза мощность шумов квантования уменьшается в 4 раза, а защищенность А₃ возрастает на 6 дБ.

Для тахпо амплитуде сигнала защищенность от шумов квантования А_3квmax = 6m— 9,2дБ, а для слабых сигналов А_3квmin = 6m— 42,2дБ.

Если требуется обеспечить защищенность от шумов квантования во всем динамическом диапазоне сигнала не менее А_3кв.тр= 30дБ, то оказывается, что потребуется

m= 12(4096N_кв). При этом защищенность для сигналов тахс амплитудой (сильных) будет более чем на 30 дБ превышать А_3кв.тр.

Большое число разрядов в коде (т = 12) при равномерном квантовании приводит к усложнению аппаратуры и неоправданному увеличению тактовой частоты. Устранить указанный существенный недостаток можно, осуществляя неравномерное квантование, которое используется в современных ЦСП. Для слабых сигналов шаг квантования выбирается и постепенно увеличивается, достигая максимальных значений для сильных сигналов (рис. 3.4б).

Источник