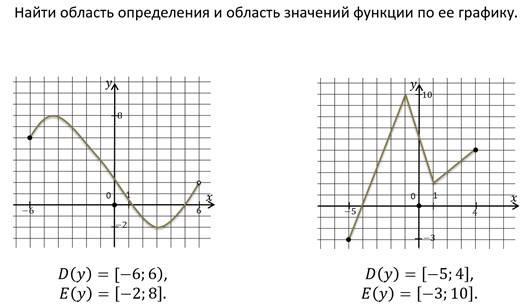
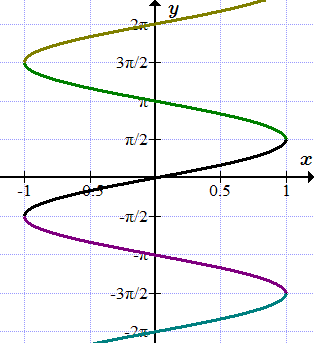Дайте определение функции что называется областью определения и областью значений
Что такое Функция?
7 класс, 11 класс, ЕГЭ/ОГЭ
Понятие функции
Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.
1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.
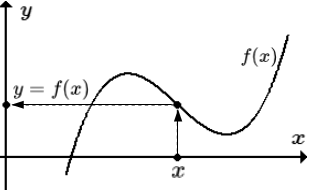
Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.
Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.
2. Функция — это определенное действие над переменной.
Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.
В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:
В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.
3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.
Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида
область определения выглядит так:
И записать это можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.
В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.
Функция. Область определения и область значений функции.
§ 1. Функции и их свойства.
п. 1. Функция. Область определения и область значений функции.
Функцией называется такая зависимость переменной у от переменной х, что каждому значению переменной х соответствует только одно значение переменной у. Переменная х называется независимой (или аргументом), а переменная у – зависимой (или значением функции).
Каждая функция имеет область определения и область значений. Разберёмся, что это такое.
Областью значений функции называется множество всех значений, которые может принимать зависимая переменная у (значение функции). Обозначается она так: .
Нахождение области значений функции задача не из простых. Её можно находить алгебраическим способом, а можно графическим. Пока мы будем использовать графический способ. Для этого необходимо построить график заданной функции и по графику определить, какие значения может принимать зависимая переменная.
Графиком функции называется множество точек на координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции. (Напомним, что абсцисса – это координата х, ордината – координата у).
Поскольку, по определению функции, каждому значению аргумента соответствует только одно значение функции, то для графика соблюдается такое же правило: каждой абсциссе графика соответствует только одно значение ординаты.
Например,
Вспомним функции, которые мы изучали в 7 и 8 классе.
Понятие функции. Область определения и область значений.
Каждая функция имеет область определения и область значений. Разберёмся, что это такое.
Областью значений функции называется множество всех значений, которые может принимать зависимая переменная у (значение функции). Обозначается она так: .
Как находить область значений функции мы рассмотрим, когда будем изучать тему «Графики функций».
Поезд находится на расстоянии 50 км от города и удаляется от него со скоростью 40 км/ч. Задайте функцию зависимости расстояния (км) от между городом и поездом от времени (ч) движения поезда.
Поезд находится на расстоянии 70 км от города и удаляется от него со скоростью 50 км/ч. Задайте функцию зависимости расстояния (км) от между городом и поездом от времени (ч) движения поезда.
Периметр прямоугольника равен 16 см, длина одной его стороны равна х см. Задайте функцию зависимости площади от стороны х.
Периметр прямоугольника равен 24 см, длина одной его стороны равна х см. Задайте функцию зависимости площади от стороны х.
Расстояние между поездами 150 км, и они удаляются друг от друга, двигаясь в противоположных направлениях, со скоростями 40 км/ч и 50 км/ч. Задайте функцию зависимости расстояния (км) между поездами от времени (ч) движения поездов.
Расстояние между поездами 180 км, и они удаляются друг от друга, двигаясь в противоположных направлениях, со скоростями 50 км/ч и 60 км/ч. Задайте функцию зависимости расстояния (км) между поездами от времени (ч) движения поездов.
Найдите область определения функций:
Задайте формулой функцию, если известно, что:
значения функции противоположны значениям аргумента;
значения функции в 2 раза больше значений аргумента;
значения функции на 3 меньше, чем удвоенные значения аргумента;
значения функции равны значениям аргумента;
значения функции в 2 раза меньше значений аргумента;
значения функции на 1 больше, чем утроенные значения аргумента.
Определение функции
Определение функции
Сложные функции
Действительные функции
В математическом анализе большую роль играют числовые функции.
Числовая функция – это функция, значениями которой являются действительные или комплексные числа.
Действительная или вещественная функция – это функция, значениями которой являются действительные числа.
Максимум и минимум
Действительные числа имеют операцию сравнения. Поэтому множество значений действительной функции может быть ограниченным и иметь наибольшее и наименьшее значения.
Верхняя и нижняя грани
Монотонные функции
Многозначные функции
Как следует из определения функции, каждому элементу x из области определения, ставится в соответствие только один элемент из множества значений. Но существуют такие отображения, в которых элемент x имеет несколько или бесконечное число образов.
Многозначная функция – это совокупность функций, определенных на некотором множестве.
Ветвь многозначной функции – это одна из функций, входящих в многозначную функцию.
Однозначная функция – это функция.
Сужение и продолжение функции
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Понятие функции. Область определения и область значений функции. Свойства функций
Урок 38. Подготовка к ОГЭ по математике 9 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Понятие функции. Область определения и область значений функции. Свойства функций»
· вспомнить основные сведения о координатной плоскости, функции;
· повторить основные свойства функции.
Начнём мы с вами с координатной плоскости.
Таким образом, мы задали на плоскости прямоугольную систему координат.
Плоскость, на которой задана система координат, называют координатной плоскостью.
Повторим определение функции.
Зависимость одной переменной у от переменной х, при которой каждому значению переменной х из определённого множества D соответствует одно определённое значение у, называется функцией от переменной х.
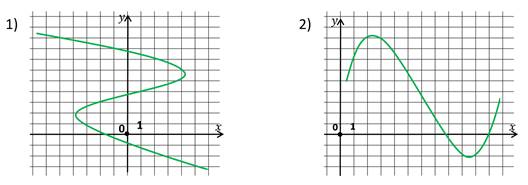
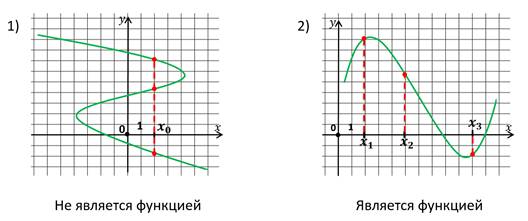
Перед нами графики двух зависимостей.
Мы должны определить, какая из них является функцией, а какая нет. В определении сказано, что только та зависимость является функцией, у которой каждому значению аргумента соответствует единственное значение функции. Давайте посмотрим на первый график.
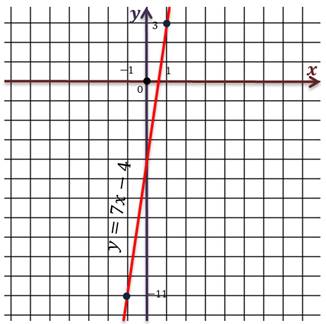
В общем виде любую функцию можно записать так y = f(x). Например, для функции y= 7x – 14 можно записать, что f(x) = 7x – 14, это одно и тоже. Под буквой f понимают некоторый набор действий над переменной x, в данном случае умножение на 7 и вычитание 14.
Переменную x называют независимой или аргументом функции, а y — зависимой (она зависит от x).
Понятно, что функция может принимать различные значения в зависимости от значения аргумента. Найдём значение каждой функции при заданном значении аргумента.
Вы заметили, что в этом задании функции и аргументы названы разными буквами. Действительно, функцию и аргумент можно называть любой буквой латинского или греческого алфавитов.
Сейчас попробуем выяснить, как же получается график функции, и дадим определение этому понятию.
f(1) = 7 · 1 – 4 = 7 – 4 =3
Получаем точку с координатами (1; 3).
Проведём прямую через полученные точки. Мы изобразили график функции y = 7x – 4.
Взяв некоторое x, мы получаем соответствующее y. Эти значения и являются координатами точек графика. Если перебрать все возможные значения x, то мы получим множество точек, изображение которых на координатной плоскости и называют графиком.
Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — значениям функции, называют графиком функции.
Существует три способа задания функции.
Функция может быть задана формулой.
Например, f(x) = 5x + 1.
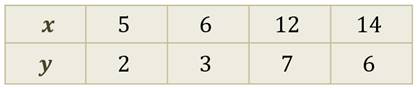
Функция может быть задана таблицей значений аргумента и функции.
Здесь сразу указаны координаты точек графика функции.
Функция можно задать словесно.
Например, каждому натуральному числу x, из отрезка [10; 20], поставлен в соответствие остаток от деления этого числа на пять. Построить график такой функции не составит труда. Для этого составим таблицу значений аргумента и функции.
Аргументами этой функции будут натуральные числа из отрезка от десяти до двадцати. А значениями функции будут остатки от деления соответствующих аргументов на пять.
Теперь давайте поговорим об основных свойствах функции.
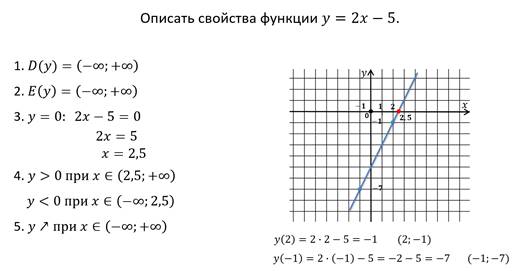
Первое свойство о котором мы поговорим – это область определения.
Все значения аргумента, т.е. переменной x образуют область определения функции (пишут D(f)),
Следующее свойство – область значений функции. Все значения зависимой переменной, т.е. y, — область значений функции (пишут E(f)). В скобках указывают букву, которой названа функция.
Область определения можно находить не только по графику функции, но и по формуле, с помощью которой задана функция.
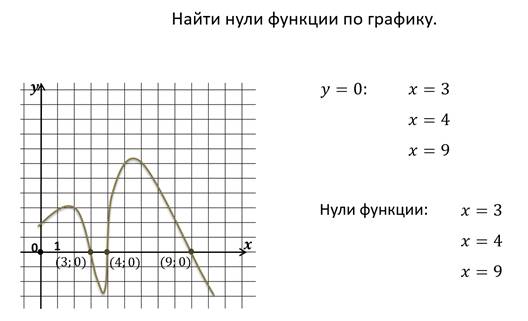
Следующее свойство, которое мы рассмотрим – нули функции.
Значения аргумента, при которых функция принимает значение, равное нулю, называют нулями функции.
В данном случае функция задана графически и мы определили нули функции по графику. Нули функции можно находить по формуле, с помощью которой задана функция.
Стоит обратить внимание на то, что не каждая функция имеет нули.
На графике это будет выглядеть так.
График не пересекает ось икс ни в одной точке.
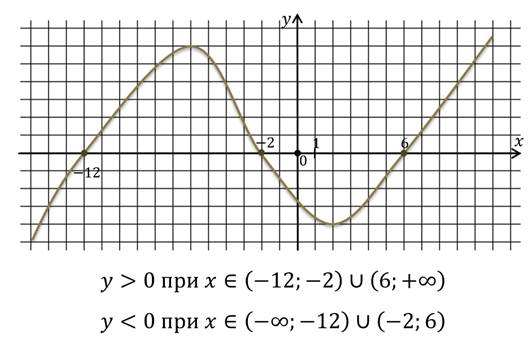
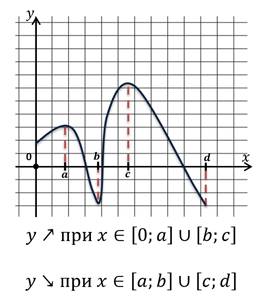
Теперь поговорим о промежутках знакопостоянства функции.
Промежутки знакопостоянства функции — это такие промежутки из области определения, на которых данная функция принимает значения только одного знака, либо положительные, либо отрицательные.
Выполните задание. Запишите промежутки знакопостоянства функции.
Осталось рассмотреть ещё одно свойство. Промежутки монотонности функции.
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции.
Функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Промежутками монотонности называют такие промежутки из области определения, на которых функция либо возрастает, либо убывает.
Найдём промежутки монотонности данной функции.
Выполним задание, где нужно описать свойства функции.
Сегодня на уроке мы повторили такие понятия как координатная плоскость, функция, график функции, повторили основные свойства функции.