Дайте определение модуля сдвига в чем состоит физический смысл этой величины
Модуль сдвига
В материаловедении модулем сдвига (обозначается буквой G или μ), называется отношение касательного напряжения к сдвиговой деформации






Модуль сдвига измеряется в ГПа (гигапаскалях).
| Материал | Значение модуля сдвига (ГПа) (при комнатной температуре) |
|---|---|
| Алмаз | 478. |
| Сталь [1] | 79.3 |
| Медь [1] | 44.7 |
| Титан | 41.4 |
| Стекло | 26.2 |
| Алюминий [1] | 25.5 |
| Полиэтилен | 0.117 |
| Резина | 0.0006 |
Модуль сдвига — одна из нескольких величин, характеризующих упругие свойства материала. Все они возникают в обобщённом законе Гука:
Модуль сдвига связан с модулем Юнга через коэффициент Пуассона:
где 
Волны
В однородных изотропных средах, существует два типа упругих волн: продольные волны и поперечные волны. Скорости продольной 

См. также
Ссылки
Модуль объёмной упругости (





Полезное
Смотреть что такое «Модуль сдвига» в других словарях:
Модуль сдвига — характеристика деформируемости, определяемая отношением интенсивности касательных напряжений к интенсивности деформаций сдвига. Остальные термины, используемые в настоящем стандарте, приведены в ГОСТ 25100. Источник: ГОСТ 30416 96: Грунты.… … Словарь-справочник терминов нормативно-технической документации
Модуль сдвига — – характеристика сопротивления материала изменению его формы при сохранении объема, численно равная отношению касательного напряжения, возникающего при чистом сдвиге, к соответствующей ему упругой деформации сдвига. [ГОСТ 23404 86] Модуль… … Энциклопедия терминов, определений и пояснений строительных материалов
модуль сдвига — Модуль 2., характеризующий сопротивление упругого материала деформациям сдвига [Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)] Тематики строительная механика, сопротивление материалов EN shear modulus DE… … Справочник технического переводчика
МОДУЛЬ СДВИГА G — определяет способность тел (г. п., м лов) сопротивляться изменению формы при сохранении их объема; равен отношению касательного напряжения t к величине угла сдвига v, определяющего искажение прямого угла между плоскостями, по которым действует… … Геологическая энциклопедия
Модуль сдвига (G) — Shear modulus Модуль сдвига (G). Отношение касательного напряжения к соответствующей деформации сдвига для касательных напряжений, меньших предела пропорциональности материала. Значения модуля сдвига обычно определяются испытанием на кручение.… … Словарь металлургических терминов
модуль сдвига — šlyties modulis statusas T sritis Standartizacija ir metrologija apibrėžtis Liestinio įtempio ir santykinės šlyjamosios deformacijos dalmuo, t. y. G = τ/γ ; čia τ – liestinis įtempis, γ – santykinė šlyjamoji deformacija. atitikmenys: angl.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
модуль сдвига — šlyties modulis statusas T sritis fizika atitikmenys: angl. modulus of rigidity; shear modulus vok. Gleitmodul, m; Schermodul, m; Schubmodul, m rus. модуль сдвига, m pranc. module de cisaillement, m; module de rigidité, m; module d’élasticité au… … Fizikos terminų žodynas
МОДУЛЬ СДВИГА — модуль 2., характеризующий сопротивление упругого материала деформациям сдвига (Болгарский язык; Български) модул на хлъзгане (Чешский язык; Čeština) modul pružnosti ve smyku (Немецкий язык; Deutsch) Schubmodul (Венгерский язык; Magyar) csúszási… … Строительный словарь
расчетное значение жесткости (модуль упругости или модуль сдвига) при пожаре — Sd,fi — [Англо русский словарь по проектированию строительных конструкций. МНТКС, Москва, 2011] Тематики строительные конструкции Синонимы Sd,fi EN design stiffness property (modulus of elasticity of shear modulus) in the fire situation … Справочник технического переводчика
динамический модуль сдвига при постоянной намагниченности — Отношение комплекса сдвигового механического напряжения к комплексу относительной деформации сдвига, вызывающей эти напряжения в образце из магнитного материала при постоянной намагниченности. Примечание При этом одна из величин механическое… … Справочник технического переводчика
Лекционный материал по теме №5
Описание
В лекции рассматриваются следующие темы:
Упругие параметры физических тел. Понятия о напряжениях и деформациях. Объемные деформации горных пород. Модуль сжатия и модуль сдвига. Модуль Юнга и коэффициент Пуассона. Коэффициенты Ламе. Закон Гука. Способы и единицы измерения упругих модулей горных пород (статические и динамические методы). Динамические характеристики упругих сред. Анизотропия параметров упругости. Скорости упругих волн и упругие модули химических элементов и минералов. Скорости упругих волн в магматических и метаморфических породах. Скорости упругих волн в пористых осадочных породах. Модели распространения упругих волн в осадочных породах. Зависимость скоростей от давления и температуры. Модели многофазных сред поглощения упругих волн.
Оглавление
1. Упругие параметры физических тел
Упругость – свойство вещества оказывать влияющей на него силе механическое сопротивление и принимать после её спада исходную форму. Противоположность упругости называется пластичность.
Упругость тел – одна из основных физических констант, связанная с внутренним строением вещества.
Упругость характеризует свойство веществ сопротивляться изменению их объема и формы (твердые тела) или только объема (жидкости, газы) под воздействием механических напряжений, что обуславливается возрастанием внутренней энергии веществ.
При упругих деформациях вещество восстанавливает свои первоначальные объем и форму после прекращения действия сил, вызывающих их деформацию. В простейших случаях малых деформаций зависимость линейная – и действует закон Гука, на котором основана теория упругости. Согласно этой теории малые деформации пропорциональны приложенной нагрузке:

где Δl/l и Δd/d –относительная продольная и поперечная деформация; F— приложенная к телу нагрузка в кг, S – площадь поперечного сечения тела в м 2 ; F/S – напряжение.
1.1. Модуль Юнга и коэффициент Пуасона
Количественными характеристиками упругих свойств являются модули упругости.
1) модуль Юнга E (модуль продольной упругости) – это отношение нормального напряжения к относительному удлинению, вызванному этим напряжением в направлении его действия. Модуль Юнга характеризует способность тел сопротивляться деформации растяжения или сжатия:

2) коэффициент Пуассона σП (коэффициент поперечного сжатия) – отношение поперечного сжатия тела при одноосном растяжении к продольному удлинению. Коэффициент Пуассона равен абсолютному значению отношения относительной поперечной деформации тела к относительной продольной деформации:


В твердых породах коэффициент Пуассона изменяется от 0,1- до 0,4. Чем больше значение коэффициента Пуассона, тем больше порода может деформироваться. Более однородные по минеральному составу породы характеризуются более низкими значениями коэффициента Пуассона.
1.2. константа Ламе и модуль сдвига

где K модуль объемного сжатия.
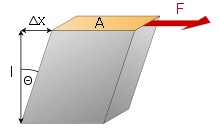
4 ) модуль сдвига G. Модуль сдвига определяет способность тел сопротивляться изменению формы при сохранении их объема:

где r – касательное напряжение; α – угол сдвига.
Модуль сдвига численно равен другой константе Ламе:

1.3. Скорости упругих волн
В телах под действием механических напряжений возникают деформации и генерируются разные по природе упругие колебания (волны) продольные p и поперечные s. Продольные волны являются результатом деформации типа сжатия – растяжения, поперечные – сдвига. В свободных газах и жидкостях возникают только продольные волны и отсутствуют поперечные.
Скорость упругих волн равна отношению длины пути соответствующей волны к времени пробега этого пути:


Для геофизиков большое значение имеют скорости, которые связаны с модулями упругости и плотностью.
Скорость продольных упругих волн или упругих колебаний, возникающих вследствие деформаций растяжение-сжатие в любой среде:

Скорость поперечных волн или упругих колебаний, возникающих вследствие деформаций сдвига в твердой среде:

Скорости vp и vs в принципе независимые величины. Связь между ними осуществляется через коэффициент Пуассона:

При сейсморазведочных работах вычисляют ряд скоростных параметров разреза: граничную, пластовую, среднюю, эффективную и лучевую скорости.
2. Динамические характеристики упругих сред
Распространение упругих колебаний сопровождается затуханием их амплитуды по мере удаления от источника. Амплитуда A гармонической волны с частотой w убывает с расстоянием l в однородной поглощающей среде по закону:

3. Скорости уругих волн и упругие характеристики химических элементов и минералов
По упругим характеристикам химические элементы весьма неоднородны. В упругой характеристике элементов играют роль их электронная оболочка, которая является упругой средой, и ядра атомов, обладающие различной массой. Упругие модули в элементах изменяются в зависимости от величины атомного радиуса элемента и его атомной массы.
Значения E, G, K, n получены для важнейших породообразующих минералов осадочных, магматических и метаморфических пород, а также для рудных минералов и чистых самородных металлов.
По модулям E, G и K минералы подразделяются на четыре группы:
Данные о скорости распространения продольных упругих волн в элементах были получены экспериментально или рассчитаны по модулям упругости.
Наблюдается корреляция с плотностью и атомными радиусами в пределах периода. Скорость увеличивается в элементах первой половины каждого периода и уменьшается в элементах второй половины каждого периода. Наибольшая зависимость скорости от атомного радиуса установлена у sp—элементов с большим размерами атомов. Зависимость скорости у sp-элементов от атомной массы – незначительна. Для d—элементов скорость в основном определяется атомной массой вещества. Скорость уменьшается при увеличении массы вещества. Это справедливо и для скоростей продольных волн и для скоростей поперечных волн. Поскольку они связаны соотношением 
Упругие свойства минералов определяются характеристиками их внутреннего строения. Наиболее информативной характеристикой является плотность упаковки атомов ω в единице объема вещества. Параметр ω обратно пропорционален атомному радиусу. Чем больше плотность упаковки, тем меньше атомный радиус. Значение параметра вычисляется по формуле (Н.З.Евзикова, Ю.В.Казицин, В.А. Рудник):

Скорость упругих волн увеличивается с ростом плотности упаковки и уменьшается с ростом средней атомной массы, являющейся мерой инерционности вещества.
Скорость продольных волн в минералах изменяется от 2000 до 18000 м/с, поперечных от 1100 до 10000 м/с. Низкие скорости характерны для самородных металлов (золото, платина), высокие – для алюмосиликатных и окисных безжелезистых минералов (топаз, шпинель, корунд), наибольшая скорость упругих волн установлена в алмазе.
Характер изменения скорости упругих волн в элементах, минералах и горных породах имеет два типа связи между скоростью продольных волн и плотностью твердых образований:


Уравнение связи между σ и vP в образованиях первого типа имеет вид:

Ко второму типу относятся тяжелые металлы, сульфиды, окисные рудные минералы и самородные металлы, состоящие преимущественно из элементов со структурой типа d. В этих элементах и минералах существенное слияние на физические параметры оказывает атомная масса. Модуль Юнга и модуль сдвига, скорость упругих волн уменьшается с ростом плотности. В минералах второго типа наблюдается некоторое уменьшение плотности упаковки атомов в веществе и значительное увеличение их средней атомной массы (от 20 до 200 а.е.м).
Таким образом, наиболее информативными характеристиками для определения упругих свойств элементов являются плотность упаковки и атомная масса. В общем виде зависимость скорости упругих волн может быть представлена выражением:

4. Скорости упругих волн в магматических и метаморфических породах
Упругие характеристики магматических и метаморфических пород определяются в значительной мере:
Основными химическими компонентами горных пород являются окислы кремния, калия, натрия, алюминия, кальция, магния и железа. Наименьшей скоростью упругих волн характеризуются породы, обогащение такими легкими окислами, как окислы кремния, калия, натрия. С уменьшением их содержания в породах возрастает содержание окислов кальция, магния, железа. Для ассоциаций горных пород, сложенных малоупругими минералами кислого состава (кварц, калиевой полевой шпат, альбит, олигоклаз) характерны минимальные скорости упругих волн. Максимальными скоростями обладают горные породы, представленные высокоупругими минералами основного состава (лабрадор, амфибол, пироксен, оливин). Таким образом, скорость упругих волн увеличивается с увеличением основности. То есть в ряду гранит-габбро-перидотит наблюдается возрастание средней скорости продольных и поперечных волн с ростом основности.
Однако следует заметить, что на упругие свойства горных пород воздействует множество факторов и не существует однозначной связи между геологическим определением породы и ее скоростной характеристикой. Породы сложенные одними и теми же минеральными ассоциациями могут отличаться по своим скоростям, так же как и совершенно разные породы могут иметь одинаковые значения скоростей. Поэтому обычно указываются пределы вероятных скоростей.
Наиболее часто встречающиеся в магматических породах величины VP и VS составляют соответственно:
гранитоиды 5,4-6,1 км/с и 2,9-3,5 км/с;
диориты 6,1-6,2 и 3,4-3,7 км/с;
анортозиты и габброиды 6-7,2 км/с и 3,5-4,1 км/с;
гипербазиты 7,4-8,2 км/с и 4-4,6 км/с.
То же наблюдается и в метаморфических породах:
гнейсы 5,6-5,9 км/с и 2,7-3,7км/с;
амфиболиты 6,2-6,8 км/с и 3,6-4 км/с;
гранулиты среднего и основного состава 6,2-6,8 км/с,
эклогиты 7,2-7,8 км/с и 4,1-4,4 км/с.
Для эффузивных пород характерен широкий диапазон значений скоростей, обусловленный различной пористостью, первоначальной структуры пород и их последующим диагенезом.
Для метаморфических пород в целом также наблюдается зависимость скорости упругих волн от минерального состава основности пород. При региональном метаморфизме скорость упругих волн возрастает от низших стадий метаморфизма к высшим за счет уплотнения пород. Причем, в кислых породах скорость упругих колебаний увеличивается на 3-5%, у пород основного состава возрастание скорости может достигать 15-25 %.
Автометаморфизм приводит к снижению скорости упругих колебаний. Процесс серпентинизации сопровождается разложением высокоупругого оливина с образованием структурно-рыхлого серпентина. Скорость снижается с 8,2 км/с до 5,5 км/с. При амфиболизации габбро-норитов и гипербазитов образуется амфиболы плагиоклазы, структурно-рыхлые хлориты, серициты, эпидоты, что также уменьшает скорость продольных волн. В неизмененных гипербазитах скорость продольных волн достигает 8,2 км/с. Скорость амфиболизированных гипербазитов равна 7,6км/с.
Процессы ультраметаморфизма приводят к уменьшению скорости упругих волн. Величина скорости продольных волн при чарнокитизации и гранитизации уменьшается до 5,5-6 км/с.
Существенное влияние на скоростные характеристики оказывают гипергенные процессы, приводящие к росту трещиноватости и образованию структурно-рыхлых минералов. Породы кислого состава в большей степени подвержены процессам выветривания. Уменьшение скорости упругих волн может при этом достигать 200-300%.
Анизотропия упругих свойств магматических и метаморфических пород обусловлена закономерных расположением порового пространства и минеральных зерен, а также кристаллической решеткой минералов. Значения скорости распространения продольных волн вдоль слоистости выше, чем измеренные перпендикулярно направлению слоистости. Коэффициент анизотропии для продольных волн достигает значений 1,2-1,3 и обычно превышает значение анизотропии для поперечных волн. Изверженные породы с массивной структурой характеризуются слабой анизотропией. Значение коэффициента анизотропии составляет 1,0-1,06. Наибольшие значения коэффициентов анизотропии наблюдаются в метаморфических породах, обладающих гнейсовидной и сланцевой текстурой. В частности биотитовые и биотит-амфиболовые гнейсы характеризуются значениями коэффициентов анизотропии 1,02-1,19, а высокоглиноземные гнейсы 1,04-1,23.
Скорости продольных волн в уплотненных осадочных породах (метаморфизованные песчаники, кристаллические известняки, доломиты) практически не отличается от скорости продольных волн, измеренных в магматических и метаморфических породах при одной и той же плотности.
5. Скорости упругих волн в осадочных породах
Упругие свойства осадочных пород определяются составом, пористостью, диагенезом пород и свойствами порового заполнителя. В общем случае скорость продольных волн в осадочных породах изменяется от 0,3 до 6,9 км/с. Отношение vP/vS различна у различных пород: в глине 0,07-0,6, в лессе 0,3-0,6, в песке 0,1-0,3. Модуль Юнга изменяется от 3 ГПа в глине до 165 ГПа в доломите. Коэффициент Пуассона изменяется в пределах 0,1-0,45.
Максимальные скорости упругих волн и модулей упругости отмечаются в уплотненных карбонатных породах, меньше величины этих параметров наблюдаются в уплотненных песчано-глинистых и гидрохимических образованиях. Зависимость между vP и σ для осадочных пород выведена М.Л.Озерской (1965):

По предложенному выражению составлены палетки со значениями vPmin, vPmax, σmax.
При пористости 1-2% скорости упругих волн в осадочных породах близки к скоростям в магматических и метаморфических породах кислого состава. В ряде случаев скорости упругих волн в доломитах сравнима со скоростями в габброидах.
Существует ряд теоретических и экспериментальных зависимостей, позволяющих оценить влияние пористости, трещиноватости, типа заполнителя пустот в породах на скорость продольных волн. Широко применяется уравнение «среднего времени», связывающего время распространения волны в объеме распространения волны в заполнителе порового пространства и минеральном скелете:

Осадочные породы – преимущественно анизотропные среды. Анизотропия скоростей упругих волн обуславливается слоистостью и направлением трещиноватости пород. Особенно ярко выражено явление анизотропии для образований с тонким переслаиванием в них глинистых пород. Коэффициент анизотропии продольных волн в этих случаях может достигать 1,2-1,3.
Фактором, влияющим на скорость упругих волн в осадочных породах, является тип заполняющего породу флюида. Насыщение порового пространства среды жидкостью, химически не взаимодействующей с минеральным скелетов породы, обуславливает увеличение скорости упругих волн. При насыщении песчаников и алевролитов раствором соли NaCl не приводящим к большому эффекту размокания присутствующих в породе глинистых минералов, скорость продольных волн увеличивается с 5-10 до 100 –120%. Влияние насыщающей жидкости на скорость связано с пористостью породы, то количественно эффект насыщения пропорционален коэффициенту пористости породы.
Насыщение глин и глинистых песчаников водой приводит к разбуханию глинистых минералов, потере связанности породы и уменьшение скорости.
Резкое возрастание сейсмических скоростей в породе вызывает замерзание воды, находящиеся в порах, кавернах, трещинах. Так как скорость продольных волн во льду почти в 2,5 раза выше, чем в воде. Поэтому скорость может возрастать на 1- 2 км/с.
Скорость увеличивается с возрастом пород, глубиной залегания, степенью цементации. Увеличение скорости с глубиной происходит из-за роста горного давления. Поскольку уменьшается пористость пород, увеличивается модуль Юнга и, соответственно, увеличивается скорость продольных волн. Это явление наиболее выражено для терригенных пород, которые отличаются высокой начальной скоростью. В карбонатных отложениях это свойство проявляется слабо, и практически не заметно для хемогенных осадков.
Переход осадочных пород из газонасыщенного в водонасыщенное состояние сопровождается изменением упругих модулей. Модуль Юнга в низкопористых образцах увеличивается до 100-120%. Модуль сдвига может как увеличиваться (на 20-30%), так и уменьшаться (до 20%).
Экспериментально установлен рост процесса поглощения α с увеличением пористости пород. Установлен рост значений αP и αS с увеличением глинистости осадочных образований.
Большое значение имеют термодинамические условия залегания нефти и газа. С повышением температуры скорость распространения упругих волн уменьшается, причем наиболее ярко в нефтенасыщенных породах (до 30%) по сравнению с газо- и водонасыщенными. Увеличение давления (глубины), наоборот, ведет к повышению скорости.
6. Методы изучения упругих свойств
Методы измерения упругих свойств можно подразделить на две большие группы, относимые к измерениям в естественном залегании и в лабораторных условиях.
Упругие модули горных пород измеряются двумя методами: статическим (изотермические) и динамическим (адиабатические модули).
Статический метод применяется для определения:
Статистические способы определения статических деформаций основываются на наблюдениях ориентированных кристаллических образцов. Для этого используют крупные образцы в виде стержней или пластин. Длина стержня должна быть значительно больше, чем размеры поперечного сечения. Полученные величины деформаций используют для расчета значений упругих параметров вещества.
Во всех случаях измерение упругих параметров сводится к непосредственному измерению деформации сжимаемых образцов тензометрами различной конструкции.
С помощью динамического метода измеряют различные виды упругих волн в веществе и их затухание. Различают:
Для определения упругой характеристики горных пород в естественном залегании применяют вертикальное сейсмическое профилирование (ВСП), сейсмический каротаж (СК), акустический каротаж и полевые сейсмические методы. Ценные сведения о скоростных характеристиках дают сейсмические исследования методом преломленных и отраженных волн, особенно в районах, где общие черты геологического строения достаточно хорошо известны.