Дайте понятия аутентификации и цифровой подписи в чем состоит их сущность
Что такое Аутентификация: Методы и Элементы
Узнайте больше о том, для чего нужна аутентификация, и ознакомьтесь с её методами
Аутентификация (англ. authentication) — это основа безопасности любой системы, которая заключается в проверке подлинности данных о пользователе сервером.
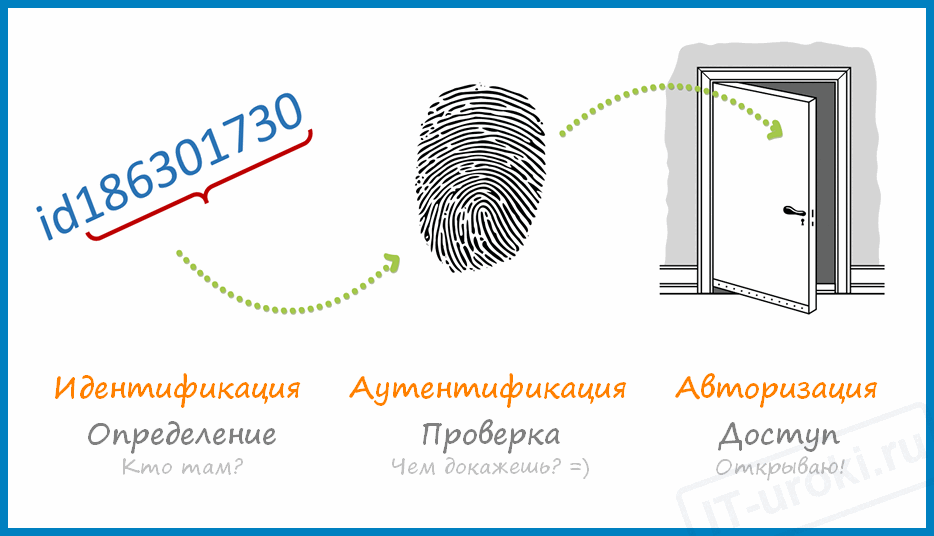
Она не тождественна идентификации и авторизации. Эти три термина являются элементами защиты информации. Первая стадия — идентификация. На ней происходит распознавание информации о пользователе, например, логин и пароль. Вторая стадия — аутентификация. Это процесс проверки информации о пользователе. Третья стадия — авторизация. Здесь происходит проверка прав пользователя и определяется возможность доступа.
Содержание
Зачем нужна аутентификация
Аутентификация нужна для доступа к:
Элементы аутентификации
Методы аутентификации
Парольные
Самый распространенный метод. Аутентификация может проходить по одноразовым и многоразовым паролям. Многоразовый пароль задает пользователь, а система хранит его в базе данных. Он является одинаковым для каждой сессии. К ним относятся PIN-коды, слова, цифры, графические ключи. Одноразовые пароли — разные для каждой сессии. Это может быть SMS с кодом.
Комбинированные
Этот метод говорит сам за себя. Аутентификация происходит с использованием нескольких методов, например, парольных и криптографических сертификатов. Он требует специальное устройство для считывания информации.
Биометрические
Это самый дорогостоящий метод аутентификации. Он предотвращает утечку или кражу персональной информации. Проверка проходит по физиологическим характеристикам пользователя, например, по отпечатку пальца, сетчатке глаза, тембру голоса и даже ДНК.
Информация о пользователе
Она используется для восстановления логина или пароля и для двухэтапной аутентификации, чтобы обеспечить безопасность. К этому методу относится номер телефона, девичья фамилия матери, год рождения, дата регистрации, кличка питомца, место проживания.
Пользовательские данные
Этот метод основывается на геоданных о местоположении пользователя с использованием GPS, а также использует информацию о точках доступа беспроводной связи. Недостаток заключается в том, что с помощью прокси-серверов можно подменить данные.
Классификация видов аутентификации
В зависимости от количества используемых методов
В зависимости от политики безопасности систем и уровня доверия
Чтобы защитить владельца сайта от злоумышленников, используют криптографические протоколы аутентификации.
Типы протоколов обусловлены тем, где происходит аутентификация — на PC или в сети.
Аутентификация на PC
Аутентификация в сети
Ресурсы
Также искали с «Аутентификация»
Оценка: 4 / 5 (18)
Начните пользоваться сервисом SendPulse прямо сегодня
Если вам интересно, что такое «✅ Аутентификация: Определение, Методы, Виды», вам может быть интересен наш сервис рассылок.
Идентификация, аутентификация и авторизация — в чем разница?
Объясняем на енотах, в чем разница между идентификацией и авторизацией, а также зачем нужна аутентификация, тем более двухфакторная.
Это происходит с каждым из нас, причем ежедневно: мы постоянно идентифицируемся, аутентифицируемся и авторизуемся в разнообразных системах. И все же многие путают значение этих слов и часто употребляют термин «идентификация» или «авторизация», когда на самом деле речь идет об аутентификации.
Ничего такого уж страшного в этом нет — пока идет бытовое общение и обе стороны диалога по контексту понимают, что в действительности имеется в виду. Но всегда лучше знать и понимать слова, которые употребляешь, а то рано или поздно нарвешься на зануду-специалиста, который вынет всю душу за «авторизацию» вместо «аутентификации», кофе среднего рода и такое душевное, но неуместное в серьезной беседе слово «ихний».
Идентификация, аутентификация и авторизация: серьезные определения
Итак, что же значат термины «идентификация», «аутентификация» и «авторизация» — и чем соответствующие процессы отличаются друг от друга? Для начала проконсультируемся с «Википедией»:
Объясняем идентификацию, аутентификацию и авторизацию на енотах
Выше было очень много умных слов, теперь давайте упростим до конкретных примеров. Скажем, пользователь хочет войти в свой аккаунт Google. Google подходит лучше всего, потому что там процедура входа явным образом разбита на несколько простейших этапов. Вот что при этом происходит:
Аутентификация без предварительной идентификации лишена смысла — пока система не поймет, подлинность чего же надо проверять, совершенно бессмысленно начинать проверку. Для начала надо представиться.
Идентификация без аутентификации — это просто глупо. Потому что мало ли кто ввел существующий в системе логин! Системе обязательно надо удостовериться, что этот кто-то знает еще и пароль. Но пароль могли подсмотреть или подобрать, поэтому лучше подстраховаться и спросить что-то дополнительное, что может быть известно только данному пользователю: например, одноразовый код для подтверждения входа.
А вот авторизация без идентификации и тем более аутентификации очень даже возможна. Например, в Google Документах можно публиковать документы так, чтобы они были доступны вообще кому угодно. В этом случае вы как владелец файла увидите сверху надпись, гласящую, что его читает неопознанный енот. Несмотря на то, что енот совершенно неопознанный, система его все же авторизовала — то есть выдала право прочитать этот документ.
А вот если бы вы открыли этот документ для чтения только определенным пользователям, то еноту в таком случае сперва пришлось бы идентифицироваться (ввести свой логин), потом аутентифицироваться (ввести пароль и одноразовый код) и только потом получить право на чтение документа — авторизоваться.
А уж если речь идет о содержимом вашего почтового ящика, то Google никогда и ни за что не авторизует неопознанного енота на чтение вашей переписки — если, конечно, он не идентифицируется с вашим логином и не аутентифицируется с вашим паролем. Но тогда это уже не будет неопознанный енот, поскольку Google однозначно определит этого енота как вас.
Теперь вы знаете, чем идентификация отличается от аутентификации и авторизации. Что еще важно понимать: аутентификация — пожалуй, самый важный из этих процессов с точки зрения безопасности вашего аккаунта. Если вы ленитесь и используете для аутентификации только слабенький пароль, то какой-нибудь енот может ваш аккаунт угнать. Поэтому:
Проблема аутентификации данных и электронная цифровая подпись
При обмене электронными документами по сети связи существенно снижаются затраты на обработку и хранение документов, убыстряется их поиск. Но при этом возникает проблема аутентификации автора документа и самого документа, т.е. установления подлинности автора и отсутствия изменений в полученном документе. В обычной (бумажной) информатике эти проблемы решаются за счет того, что информация в документе и рукописная подпись автора жестко связаны с физическим носителем (бумагой). В электронных документах на машинных носителях такой связи нет.
Целью аутентификации электронных документов является их защита от возможных видов злоумышленных действий, к которым относятся:
Эти виды злоумышленных действий могут нанести существенный ущерб банковским и коммерческим структурам, государственным предприятиям и организациям, а также частным лицам, применяющим в своей деятельности компьютерные информационные технологии.
При обработке документов в электронной форме совершенно непригодны традиционные способы установления подлинности по рукописной подписи и оттиску печати на бумажном документе. Принципиально новым решением является электронная цифровая подпись (ЭЦП).
Электронная цифровая подпись используется для аутентификации текстов, передаваемых по телекоммуникационным каналам. Функционально она аналогична обычной рукописной подписи и обладает ее основными достоинствами:
· удостоверяет, что подписанный текст исходит от лица, поставившего подпись;
· не дает самому этому лицу возможности отказаться от обязательств, связанных с подписанным текстом;
· гарантирует целостность подписанного текста.
Цифровая подпись представляет собой относительно небольшое количество дополнительной цифровой информации, передаваемой вместе с подписываемым текстом.
Каждая подпись содержит следующую информацию:
· срок окончания действия ключа данной подписи;
· информацию о лице, подписавшем файл (Ф.И.0., должность, краткое наименование фирмы);
· идентификатор подписавшего (имя открытого ключа);
· собственно цифровую подпись.
Система ЭЦП включает две процедуры:
1) процедуру постановки подписи;
2) процедуру проверки подписи.
При формировании ЭЦП отправитель прежде всего вычисляет хэш-функцию h(М) подписываемого текста М. Вычисленное значение хэш-функции h(М) представляет собой один короткий блок информации m, характеризующий весь текст М в целом. Затем число m шифруется секретным ключом отправителя. Получаемая при этом пара чисел представляет собой ЭЦП для данного текста М.
При проверке ЭЦП получатель сообщения снова вычисляет хэш-функцию m = h(М)принятого по каналу текста М, после чего при помощи открытого ключа отправителя проверяет, соответствует ли полученная подпись вычисленному значению m хэш-функции.
Принципиальным моментом в системе ЭЦП является невозможность подделки ЭЦП пользователя без знания его секретного ключа подписывания.
В качестве подписываемого документа может быть использован любой файл. Подписанный файл создается из неподписанного путем добавления в него одной или более электронных подписей.
Использование хэш-функций
Поскольку подписываемые документы — переменного (и как правило достаточно большого) объёма, в схемах ЭП зачастую подпись ставится не на сам документ, а на его хэш.
Для вычисления хэша используются криптографические хэш-функции, что гарантирует выявление изменений документа при проверке подписи. Хэш-функции не являются частью алгоритма ЭП, поэтому в схеме может быть использована любая надёжная хэш-функция.
Использование хэш-функций даёт следующие преимущества:
· Вычислительная сложность. Обычно хэш цифрового документа делается во много раз меньшего объёма, чем объём исходного документа, и алгоритмы вычисления хэша являются более быстрыми, чем алгоритмы ЭП. Поэтому формировать хэш документа и подписывать его получается намного быстрее, чем подписывать сам документ.
· Совместимость. Большинство алгоритмов оперирует со строками бит данных, но некоторые используют другие представления. Хэш-функцию можно использовать для преобразования произвольного входного текста в подходящий формат.
· Целостность. Без использования хэш-функции большой электронный документ в некоторых схемах нужно разделять на достаточно малые блоки для применения ЭП. При верификации невозможно определить, все ли блоки получены и в правильном ли они порядке.
Использование хэш-функции не обязательно при электронной подписи, а сама функция не является частью алгоритма ЭП, поэтому хэш-функция может использоваться любая или не использоваться вообще.
В большинстве ранних систем ЭП использовались функции с секретом, которые по своему назначению близки к односторонним функциям. Такие системы уязвимы к атакам с использованием открытого ключа (см. ниже), так как, выбрав произвольную цифровую подпись и применив к ней алгоритм верификации, можно получить исходный текст. ] Чтобы избежать этого, вместе с цифровой подписью используется хэш-функция, то есть, вычисление подписи осуществляется не относительно самого документа, а относительно его хэша. В этом случае в результате верификации можно получить только хэш исходного текста, следовательно, если используемая хэш-функция криптографически стойкая, то получить исходный текст будет вычислительно сложно, а значит атака такого типа становится невозможной.
Симметричная схема
Симметричные схемы ЭП менее распространены чем асимметричные, так как после появления концепции цифровой подписи не удалось реализовать эффективные алгоритмы подписи, основанные на известных в то время симметричных шифрах. Первыми, кто обратил внимание на возможность симметричной схемы цифровой подписи, были основоположники самого понятия ЭП Диффи и Хеллман, которые опубликовали описание алгоритма подписи одного бита с помощью блочного шифра. [2] Асимметричные схемы цифровой подписи опираются на вычислительно сложные задачи, сложность которых еще не доказана, поэтому невозможно определить, будут ли эти схемы сломаны в ближайшее время, как это произошло со схемой, основанной на задаче об укладке ранца. Также для увеличения криптостойкости нужно увеличивать длину ключей, что приводит к необходимости переписывать программы, реализующие асимметричные схемы, и в некоторых случаях перепроектировать аппаратуру. [7] Симметричные схемы основаны на хорошо изученных блочных шифрах.
В связи с этим симметричные схемы имеют следующие преимущества:
· Стойкость симметричных схем ЭП вытекает из стойкости используемых блочных шифров, надежность которых также хорошо изучена.
· Если стойкость шифра окажется недостаточной, его легко можно будет заменить на более стойкий с минимальными изменениями в реализации.
Однако у симметричных ЭП есть и ряд недостатков:
· Нужно подписывать отдельно каждый бит передаваемой информации, что приводит к значительному увеличению подписи. Подпись может превосходить сообщение по размеру на два порядка.
· Сгенерированные для подписи ключи могут быть использованы только один раз, так как после подписывания раскрывается половина секретного ключа.
Из-за рассмотренных недостатков симметричная схема ЭЦП Диффи-Хелмана не применяется, а используется её модификация, разработанная Березиным и Дорошкевичем, в которой подписывается сразу группа из нескольких бит. Это приводит к уменьшению размеров подписи, но к увеличению объема вычислений. Для преодоления проблемы «одноразовости» ключей используется генерация отдельных ключей из главного ключа. [7]
Асимметричная схема
Асимметричные схемы ЭП относятся к криптосистемам с открытым ключом. В отличие от асимметричных алгоритмов шифрования, в которых шифрование производится с помощью открытого ключа, а расшифровка — с помощью закрытого, в схемах цифровой подписи подписание производится с применением закрытого ключа, а проверка подписи — с применением открытого.
Схема, поясняющая алгоритмы подписи и проверки
Общепризнанная схема цифровой подписи охватывает три процесса:
· Генерация ключевой пары. При помощи алгоритма генерации ключа равновероятным образом из набора возможных закрытых ключей выбирается закрытый ключ, вычисляется соответствующий ему открытый ключ.
· Формирование подписи. Для заданного электронного документа с помощью закрытого ключа вычисляется подпись.
· Проверка (верификация) подписи. Для данных документа и подписи с помощью открытого ключа определяется действительность подписи.
Для того, чтобы использование цифровой подписи имело смысл, необходимо выполнение двух условий:
· Верификация подписи должна производиться открытым ключом, соответствующим именно тому закрытому ключу, который использовался при подписании.
· Без обладания закрытым ключом должно быть вычислительно сложно создать легитимную цифровую подпись.
Следует отличать электронную цифровую подпись от кода аутентичности сообщения (MAC).
Виды асимметричных алгоритмов
Как было сказано выше, чтобы применение ЭП имело смысл, необходимо, чтобы вычисление легитимной подписи без знания закрытого ключа было вычислительно сложным процессом.
Обеспечение этого во всех асимметричных алгоритмах цифровой подписи опирается на следующие вычислительные задачи:
· Задачу дискретного логарифмирования (EGSA)
· Задачу факторизации, то есть разложения числа на простые множители (RSA)
Алгоритмы ЭП подразделяются на: обычные цифровые подписи и на цифровые подписи с восстановлением документа
При верификации цифровых подписей с восстановлением документатело документа восстанавливается автоматически, его не нужно прикреплять к подписи.
Обычные цифровые подписи требуют присоединение документа к подписи.
Все алгоритмы, подписывающие хэш документа, относятся к обычным ЭП.
К ЭП с восстановлением документа относится, в частности, RSA.
Схемы электронной подписи могут быть одноразовыми и многоразовыми.
В одноразовых схемах после проверки подлинности подписи необходимо провести замену ключей.
В многоразовых схемах замена ключей не требуется.
Детерминированные ЭП при одинаковых входных данных вычисляют одинаковую подпись.
Реализация вероятностных алгоритмов более сложна, так как требует надежный источник энтропии, но при одинаковых входных данных подписи могут быть различны, что увеличивает криптостойкость.
В настоящее время многие детерминированные схемы модифицированы в вероятностные.
В некоторых случаях, таких как потоковая передача данных, алгоритмы ЭП могут оказаться слишком медленными. В таких случаях применяется быстрая цифровая подпись. Ускорение подписи достигается алгоритмами с меньшим количеством модульных вычислений и переходом к принципиально другим методам расчета.
Перечень алгоритмов ЭП
Асимметричные схемы:
· FDH (Full Domain Hash), вероятностная схема RSA-PSS (Probabilistic Signature Scheme), схемы стандарта PKCS#1 и другие схемы, основанные на алгоритме RSA
· Американские стандарты электронной цифровой подписи: DSA, ECDSA (ECDSA на основе аппарата эллиптических кривых)
· Российские стандарты электронной цифровой подписи: ГОСТ Р 34.10-94 (в настоящее время не действует), ГОСТ Р 34.10-2012
· Украинский стандарт электронной цифровой подписи ДСТУ 4145-2002
· Белорусский стандарт электронной цифровой подписи СТБ 1176.2-99
· Pointcheval-Stern signature algorithm
· Вероятностная схема подписи Рабина
· Схема BLS (Boneh-Lynn-Shacham)
· Схема GMR (Goldwasser-Micali-Rivest)
На основе асимметричных схем созданы модификации цифровой подписи, отвечающие различным требованиям:
· Групповая цифровая подпись
· Неоспоримая цифровая подпись
· «Слепая» цифровая подпись и справедливая «слепая» подпись
· Конфиденциальная цифровая подпись
· Цифровая подпись с доказуемостью подделки
· Доверенная цифровая подпись
· Разовая цифровая подпись
Выводы
В последнее время все чаще возникает вопрос о замене в системах передачи и обработки информации рукописной подписи, подтверждающей подлинность того или иного документа, ее электронным аналогом — электронной цифровой подписью (ЭЦП). Ею могут скрепляться всевозможные электронные документы, начиная с различных сообщений и кончая контрактами. ЭЦП может применяться также для контроля доступа к особо важной ин- формации. К ЭЦП предъявляются два основных требования: высокая сложность фальсификации и легкость проверки.
Для реализации ЭЦП можно использовать как классические криптографические алгоритмы, так и асимметричные, причем именно последние обладают всеми свойствами, необходимыми для ЭЦП.
Однако ЭЦП чрезвычайно подвержена действию обобщенного класса программ «троянский конь» с преднамеренно заложенными в них потенциально опасными последствиями, активизирующимися при определенных условиях. Например, в момент считывания файла, в котором находится подготовленный к подписи документ, эти программы могут изменить имя подписывающего лица, дату, какие-либо данные (например, сумму в платежных документах) и т.п.
Поэтому при выборе системы ЭЦП предпочтение безусловно должно быть отдано ее аппаратной реализации, обеспечивающей надежную защиту информации от несанкционированного доступа, выработку криптографических ключей и ЭЦП.
Цифровые подписи на основе шифрсистем с открытыми ключами
Идея использования систем шифрования с открытыми ключами для
построения систем цифровой подписи как бы заложена в постановке задачи.
Действительно, пусть имеется пара преобразований (Е, D), первое из которых
зависит от открытого ключа, а второе — от секретного. Для того чтобы
вычислить цифровую подпись S для сообщения, владелец секретного ключа
может применить к сообщению М второе преобразование D: S = D(M). В
таком случае вычислить подпись может только владелец секретного ключа, в
то время как проверить равенство E(S) = М может каждый. Основными
требованиями к преобразованиям Е и D являются:
— выполнение равенства М = E(D(M)) для всех сообщений М;
— невозможность вычисления значения D(M) для заданного
сообщения М без знания секретного ключа.
Отличительной особенностью предложенного способа построения
цифровой подписи является возможность отказаться от передачи самого
подписываемого сообщения М, так как его можно восстановить по значению
подписи. В связи с этим подобные системы называют схемами цифровой
подписи с восстановлением текста.
Заметим, что если при передаче сообщение дополнительно шифруется
с помощью асимметричного шифра, то пара преобразований (Е, D),
используемая в схеме цифровой подписи, должна отличаться от той, которая
используется для шифрования сообщений. В противном случае появляется
возможность передачи в качестве шифрованных ранее подписанных
сообщений. При этом более целесообразно шифровать подписанные данные,
чем делать наоборот, то есть подписывать шифрованные данные, поскольку в
первом случае противник получит только шифртекст, а во втором — и
открытый, и шифрованный тексты.
Очевидно, что рассмотренная схема цифровой подписи на основе пары
преобразований (Е, D) удовлетворяет требованию невозможности подделки,
в то время как требование невозможности создания подписанного сообщения
не выполнено: для любого значения S каждый может вычислить значение М
= E(S) и тем самым получить подписанное сообщение.
Требование невозможности подмены сообщения заведомо
выполняется, так как преобразование Е взаимно однозначно.
Для защиты от создания злоумышленником подписанного сообщения
можно применить некоторое взаимно-однозначное отображение R :M a M
вносящее избыточность в представление исходного сообщения, например,
его длины, а затем уже вычислять подпись S = D(M
злоумышленник, подбирая S и вычисляя значения M
сталкиваться с проблемой отыскания таких значений M
существует прообраз М. Если отображение R выбрано таким, что число
возможных образов M
значительно меньше числа всех возможных
последовательностей той же длины, то задача создания подписанного
сообщения будет сложной.
Другой подход к построению схем цифровых подписей на основе
систем шифрования с открытым ключом состоит в использовании
бесключевых хеш-функций. Для заданного сообщения М сначала
вычисляется значение хеш-функции h(M), а затем уже значение подписи S =
D(h(M)). Ясно, что в таком случае по значению подписи уже нельзя восста-
новить сообщение. Поэтому подписи необходимо передавать вместе с
сообщениями. Такие подписи получили название цифровых подписей с
дополнением. Заметим, что системы подписи, построенные с использованием
бесключевых хеш-функций, заведомо удовлетворяют всем требованиям,
предъявляемым к цифровым подписям. Например, невозможно создание
сообщения с известным значением подписи, поскольку бесключевая хеш-
функция должна быть однонаправленной.
В качестве системы шифрования с открытыми ключами можно
использовать, например, систему RSA.
Цифровая подпись Фиата — Шамира
Рассмотрим подход к построению схемы цифровой подписи,
основанной на сложности задач факторизации больших целых чисел и
извлечения квадратного корня в кольце вычетов. Идея построения схемы
принадлежит А. Фиату и А. Шамиру. Приведем одну из модификаций схемы,
предложенную ими совместно с У. Фейджем. В ней реализуется цифровая
подпись с дополнением.
Пусть h — некоторая хеш-функция, преобразующая исходное
сообщение в битовую строку длины т. Выберем различные простые числа р
ключом объявляется набор чисел b1,b2. bm ∈ Zn, где
Алгоритм вычисления цифровой подписи для сообщения М состоит в
выполнении следующих действий:
2. Вычислить и = r2 mod п ; 3. Вычислить h(M,u) =s=(sl,s2. sm);
4. Вычислить Π=mist r ai n i1mod ;
5. Подписью для сообщения М положить пару (s, t).
Алгоритм проверки подписи состоит в выполнении следующих
1. По открытому ключу b1, b2. bт mod n и значению t вычислить
Π= m w t b i n
2. Вычислить h(M,w) = s’;
3. Проверить равенство s = s’. Достоинствами описанной схемы
являются возможность выработки цифровых подписей для нескольких
различных сообщений с использованием одного секретного ключа, а также
сравнительная простота алгоритмов вычисления и проверки подписи.
Например, для схемы цифровой подписи, основанной на алгоритме RSA,
соответствующие алгоритмы требуют выполнения значительно большего
числа умножений. Попытка компрометации этой схемы сталкивается с не-
обходимостью решения сложной задачи нахождения квадратных корней по
Недостатком схемы является большая длина ключа, которая
определяется числом т. Если двоичная запись числа п содержит l знаков, то
длина секретного ключа составляет ml бит, а открытого ключа — (т +1)l бит.
При этом необходимо учитывать, что для обеспечения достаточной
стойкости данной схемы цифровой подписи числа l и т должны иметь в
своей двоичной записи несколько сотен бит.
Подписи EIGamal
Чтобы подписать сообщение М, сначала выбирается случайное число k,
взаимно простое с р-1. Затем вычисляется
и с помощью расширенного алгоритма Эвклида находится b в
Подписью является пара чисел: а и b. Случайное __________значение k должно
храниться в секрете. Для проверки подписи нужно убедиться, что
yaab mod p = gM mod p
Каждая подпись или шифрование EIGamal требует нового значения k,
и это значение должно быть выбрано случайным образом. Если когда-нибудь
злоумышленник раскроет k, используемое отправителем, он сможет раскрыть
закрытый ключ отправителя х. Если злоумышленник когда-нибудь сможет
получить два сообщения, подписанные или зашифрованные с помощью
одного и того же k, то он сможет раскрыть х, даже не зная значение k.
Подписи EIGamalНапример, выберем p = 11 и g = 2, а закрытый ключ х = 8. Вычислим
у = gx modp = 28 mod 11=3
Открытым ключом являются у = 3, g = 2 и p = 11. Чтобы подписать М=
5, сначала выберем случайное число k=9. Убеждаемся, что НОД(9, 10)= 1.
а = gk mod p = 29 mod 11=6
и с помощью расширенного алгоритма Эвклида находим b:
5 = (8*6 + 9*b) mod 10
Решение: b = 3, а подпись представляет собой пару: а = 6 и b = 3.
Для проверки подписи убедимся, что
yaab mod p = gM mod p
36 63 mod 11=25 mod 11
Томас Бет (Thomas Beth) изобрел вариант схемы EIGamal, подходящий
для доказательства идентичности. Существуют варианты для проверки под-
линности пароля и для обмена ключами. И еще тысячи и тысячи других.
DSA представляет собой вариант алгоритма подписи ElGamal.
Алгоритм использует следующие параметры:
р = простое число длиной L битов, где L принимает значение, кратное 64, в диапазоне от 512 до 1024. (В первоначальном стандарте размер р был
фиксирован и равен 512 битам. Это вызвало множество критических
Mod p больше 1.
х = число, меньшееq.
y = gx mod p.
В алгоритме также используется однонаправленная хэш-функция:
Н(т). Стандарт определяет использование SHA.
Первые три параметра, р, q и g, открыты и могут быть общими для
подписать сообщение, т:
(1)Отправитель генерирует случайное число k, меньшее q
r = (gk mod p) mod q
s = (k-1 (Н(т) + xr)) mod q
Подписью служат параметры r и s, она посылает их получателю.
(3) Получатель проверяет подпись, вычисляя
w = s-1 mod q
u1 = (Н(т) * w) mod q
u2 = (rw) mod q
v = ((gu1 *yu2) mod p) mod q
Если v = r, то подпись правильна.
Алгоритм цифровой подписи ГОСТ Р 34.10-94
Алгоритм основан на DSA, и использует следующие параметры
р = простое число, длина которого либо между 509 и 512 битами, либо
до 256 битов. а = любое число, меньшее р-1, для которого aq mod p = 1.
х = число, меньшее q. у = ах mod p.
Этот алгоритм также использует однонаправленную хэш-функцию:
Н(х). Стандарт определяет использование хэш-функции ГОСТ Р 34.11-94,
основанной на симметричном алгоритме ГОСТ 28147-89.
Первые три параметра, p, q и а, открыты и могут использоваться
Чтобы подписать сообщение т
(1) Отправитель генерирует случайное число k, меньшее q
(2) Отправитель генерирует
I = (a* mod p) mod q
s = (ct + k(H(m))) mod q
r = (ak mod p) mod q
s = (xr + k(H(m))) mod q
Если H(m) mod q =0, то значение хэш-функции устанавливается
равным 1. Если r =0, то выберите другое значение k и начните снова.
Подписью служат два числа: r mod 2256 и s mod 2256, отправитель посылает их
(3) Получатель проверяет подпись, вычисляя v = H(m)q-2 mod q
Если и = r, то подпись правильна.
Различие между этой схемой и DSA в том, что в DSA s = (k-1 (H(m) +
xr)) mod q, что дает другое уравнение проверки.
Деревья цифровых подписей
Ральф Меркл предложил систему цифровых подписей, основанную на
криптографии с секретным ключом, создающей бесконечное количество
одноразовых подписей, используя древовидную структуру. Основной идеей
этой схемы является поместить корень дерева в некий открытый файл,
удостоверяя его таким образом. Корень подписывает одно сообщение и
удостоверяет подузлы дерева. Каждый из этих узлов подписывает одно
сообщение и удостоверяет свои подузлы, и так далее.
Подпись документа с помощью криптографии с открытыми ключами
Существуют алгоритмы с открытыми ключами, которые можно
закрытый ключ. Зашифруйте документ своим закрытым ключом, и вы
который невозможно использовать для шифрования. Эта идея впервые была
изобретена Диффи и Хеллманом и в дальнейшем была расширена и
углублена в других работах. Основной протокол прост:
(1) Отправитель шифрует документ своим закрытым ключом, таким
образом, подписывая его.
(2) Отправитель посылает подписанный документ получателю.
(3) Получатель расшифровывает документ, используя открытый ключ
отправителя, таким образом проверяя подпись.
Такая подпись соответствует всем требованиям:
1. Эта подпись достоверна. Когда получатель расшифровывает
сообщение с помощью открытого ключа отправителя, происходит проверка
2. Эта подпись неподдельна. Только отправитель знает свой закрытый
3. Эту подпись нельзя использовать повторно. Подпись является
функцией документа и не может быть перенесена на другой документ.
4. Подписанный документ нельзя изменить. После любого изменения
документа подпись не сможет больше подтверждаться открытым ключом
5. От подписи невозможно отказаться.
Метки времени
На самом деле, при определенных условиях получатель может
повторно использовать документ и подпись совместно.
Поэтому в цифровые подписи часто включают метки времени. Дата и
время подписания документа добавляются к документу и подписываются
вместе со всем содержанием сообщения. Таким образом, использовать
документа повторно становится невозможно.
Подпись документа с помощью криптографии с открытыми ключами и
однонаправленных хэш-функций
На практике алгоритмы с открытыми ключами часто недостаточно
эффективны для подписи больших документов. Для экономии времени
протоколы цифровой подписи нередко используют вместе с
однонаправленными хэш-функциями. Отправитель подписывает не
документ, а значение хэш-функции для данного документа. В этом протоколе
однонаправленная хэш-функция и алгоритм цифровой подписи
(1) Отправитель получает значение однонаправленной хэш-функции
(2) Отправитель шифрует это значение своим закрытым ключом, таким
образом подписывая документ.
(3) Отправитель посылает получателю документ и подписанное
(4) Получатель получает значение однонаправленной хэш-функции для
документа, присланного отправителем. Затем, используя алгоритм цифровой
подписи, он расшифровывает подписанное значение хэш-функции с
помощью открытого ключа отправителя. Если подписанное значение хэш-
функции совпадает с рассчитанным, подпись правильна.
Скорость заметно возрастает и, так как вероятность получить для двух
различных документов одинаковое 160-битное значение хэш-функции
cоставляет только один шанс из 2160, можно безопасно приравнять подпись
значения хэш-функции и подпись документа. Должна использоваться только
однонаправленная хэш-функция, иначе создать разные документы с одним и
тем же значением хэш-функции нетрудно, и подпись одного документа
приведет к ошибочной подписи сразу многих документов.
У протокола есть и другие выгоды. Во-первых, подпись может быть
отделена от документа. Во-вторых, значительно уменьшаются требования к
объему памяти получателя, в котором хранятся документы и подписи. Ар-
хивная система может использовать этот протокол для подтверждения
существования документов, не храня их содержания. В центральной базе
данных могут храниться лишь значения хэш-функции для файлов. Вовсе не
нужно просматривать файлы, пользователи помещают свои значения хэш-
функции в базу данных, а база данных хранит эти значения, помечая их
временем получения документа. Если в будущем возникнет какое-нибудь
разногласие по поводу автора и времени создания документа, база данных
сможет разрешить его при помощи хранящегося в ней значения хэш-