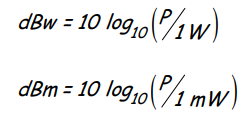Дбн гц что это

СОДЕРЖАНИЕ

Определения

Рассмотрим следующий бесшумный сигнал:

Фазовый шум добавляется к этому сигналу путем добавления к сигналу случайного процесса, представленного символом φ, следующим образом:

Преобразования джиттера

джиттер (секунды ) знак равно фазовая ошибка ( ∘ ) 360 ∘ × частота (герц) <\ displaystyle <\ text >) = <\ frac <<\ text <фазовая ошибка (>> <> ^ <\ circ><\ text <)>>> <360 ^ <\ circ>\ раз <\ text <частота (герц)>>>>>

При отсутствии шума 1 / f в области, где фазовый шум имеет наклон –20 дБн / декаду ( уравнение Лисона ), среднеквадратичное дрожание цикла может быть связано с фазовым шумом следующим образом:

L ( ж ) знак равно ж ос 3 σ c 2 ж 2 <\ displaystyle <\ mathcal > \ left (f \ right) = <\ frac > ^ <3>\ sigma _ ^ <2>> >>>

Измерение

Системы измерения фазового шума являются альтернативой анализаторам спектра. Эти системы могут использовать внутренние и внешние эталоны и позволяют измерять как остаточный (аддитивный), так и абсолютный шум. Кроме того, эти системы могут выполнять измерения с низким уровнем шума, близким к несущей.

Спектральная чистота

Синусоидальный выходной сигнал идеального генератора представляет собой единственную линию в частотном спектре. Такая идеальная спектральная чистота недостижима в практическом генераторе. Расширение спектральной линии, вызванное фазовым шумом, должно быть минимизировано в гетеродинном генераторе супергетеродинного приемника, потому что это противоречит цели ограничения частотного диапазона приемника фильтрами в усилителе промежуточной частоты.

Источник

дБ, дБм, дБВт, дБн Основы: в чем разница между ними?

В ВЧ- и СВЧ-измерениях обычно используются такие единицы, как дБ, дБм, дБн и дБВт. Эти термины могут показаться запутанными, но на самом деле они довольно хороши. легко понять.

В этой короткой статье мы рассмотрим разницу между этими терминами и навсегда разрешите эту путаницу!

Итак, вот уравнение, о котором нужно помнить:

дБ = 10 log (Power2 / Power1) （Power2 / Power1 безразмерно! ）

Это относительное значение между двумя уровнями мощности.

О: Многие значения безразмерны, например, отношения и коэффициенты.

2. дБм или децибел относительно уровня мощности 1 мВт

Это абсолютное значение (поскольку оно измеряется относительно фиксированного ссылка).

дБ = 10 log (мощность2 / 1 мВт)

Мощность в РЧ-измерениях обычно выражается в дБмВт.

Так какая же мощность в дБм при 1 мВт? Конечно 0 дБм!

Следовательно, dBw и dBm выражают Prelative как 1 Вт и 1 мВт соответственно！

Примечание: Аргументом функции log10 является коэффициент (т. Е. Безразмерный).

Например,
20 дБм означает 100 x 1 мВт = 100 мВт
3 дБВт означает 2 x 1 Вт = 2 Вт

Будьте осторожны при вычислениях с децибелами!

Стандартные значения в дБ
Обратите внимание, что 10 log10 (10) = 10.
Поэтому говорят, что усилитель с коэффициентом усиления G = 10 имеет усиление 10 дБ.

3. дБВт или децибел относительно уровня мощности 1 Вт.

дБВт не сильно отличается от дБм с той лишь разницей, что мы просто используйте 1 Вт в качестве эталона вместо 1 мВт в дБмВт.

дБ = 10 log (мощность2 / 1 Вт)

Это абсолютная величина.

4. дБн или децибел относительно уровня мощности несущей

Обычно это используется для указания таких параметров, как SFDR (Spurious Free Dynamic Range), гармоники и т. Д., Которые имеют большее значение, когда мощность основной несущей в перспективе

+30 дБм = 1 Вт = 0 дБВт

Я считаю, что вы, ребята, можете отличить дБ, дБм, дБВт, дБн.

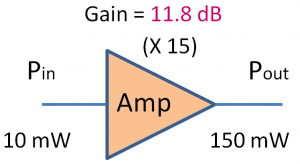
Q1. Подайте 10 мВт на РЧ-усилитель, и измеренная мощность составит 150 мВт. Каков коэффициент усиления в дБ этого усилителя?

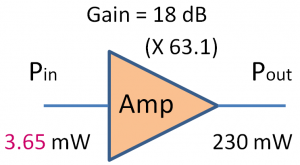
Q2. Коэффициент усиления ВЧ усилителя составляет 18 дБ, если измеренная выходная мощность составляет 230 мВт, то какова входная мощность?

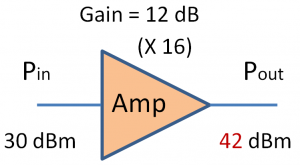
Q3. Насколько 12 дБ больше 30 дБмВт?

Ответ 1
Поскольку Pin = 10 мВт и Pout = 150 мВт
Усиление (дБ) = 10log (150/10) = 11.8 дБ

Ответ 2
* Поскольку Pout = 230 мВт и усиление = 18 дБ
* 10log (230 / Pin) = 18 дБ
* Журнал (230 / контактный) = (18/10) = 1.8
* 101.8 = 230 / контактный
*Therefore, Pin=230/(101.8)=230/63.1=3.65 mW

И мы можем удобно сказать,

30 дБм (1 Вт) + 12 дБ (x 16) = 42 дБм (16 Вт)

Правильно ли вы поняли your Жду вашего комментария!

Источник

О децибелах для радиоинженеров

Узнайте о децибелах и их вариациях в контексте радиочастотного проектирования и тестирования.

Радиотехника, как и все научные дисциплины и подразделы, включает в себя довольно много специализированной терминологии. Одним из наиболее важных слов, которые вам понадобятся при работе в мире радиочастот, является «дБ» (и некоторые его варианты). Если вы глубоко закрепились в проектировании радиочастотных систем, то можете обнаружить, что слово «дБ» становится вам таким же знакомым, как и ваше собственное имя.

Как вы, наверное, знаете, дБ означает децибел. Это логарифмическая единица, которая обеспечивает удобный способ работы с отношениями, такими как отношение между амплитудами входного и выходного сигналов.

Отношение напряжений сигналов на выходе и входе усилителя

Мы не будем описывать общую информацию о децибелах, потому что она уже доступна на этой странице учебника «Основы электроники и схемотехники». Вместо этого мы сосредоточимся на практических аспектах децибелов в конкретном контексте радиочастотных систем.

Относительный, не абсолютный

Легко забыть, что дБ является относительной единицей. Вы не можете сказать: «Выходная мощность составляет 10 дБ».

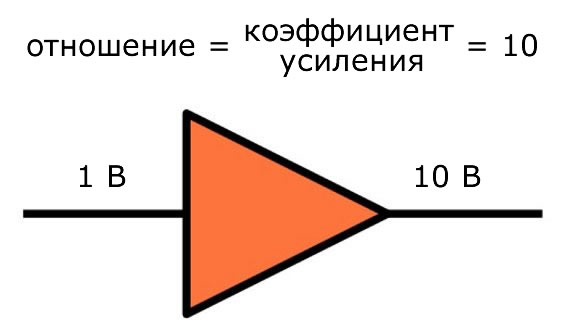
Напряжение является абсолютной величиной, потому что мы всегда говорим о разности потенциалов между двумя точками; обычно мы имеем в виду потенциал одного узла относительно узла земли 0 В. Ток также является абсолютной величиной, поскольку единица измерения (ампер) включает в себя определенное количество заряда в течение определенного количества времени. Децибел, напротив, это единица измерения, которая включает в себя логарифм отношения между двумя числами. Ярким примером является коэффициент усиления усилителя: если мощность входного сигнала равна 1 Вт, а мощность выходного сигнала равна 5 Вт, мы имеем коэффициент 5:

\[10 \log_ <10>\left( < P_<вых>\over P_ <вх>> \right) = 10 \log_ <10>(5) \approx 7 дБ\]

Таким образом, этот усилитель обеспечивает усиление по мощности 7 дБ, то есть соотношение между мощностью выходного сигнала и мощностью входного сигнала может быть выражено как 7 дБ.

Почему дБ?

Конечно, можно было бы проектировать и тестировать радиочастотные системы без использования дБ, но на практике дБ используются везде. Одно из преимуществ заключается в том, что шкала дБ позволяет выражать очень большие отношения без использования очень больших чисел: усиление по мощности в 1 000 000 раз составляет всего 60 дБ. Кроме того, при использовании дБ легко вычисляется общий коэффициент усиления или потерь в цепи прохождения сигнала, поскольку отдельные значения в дБ просто складываются (тогда как, если бы мы работали с обычными отношениями, нам потребовалось бы умножение).

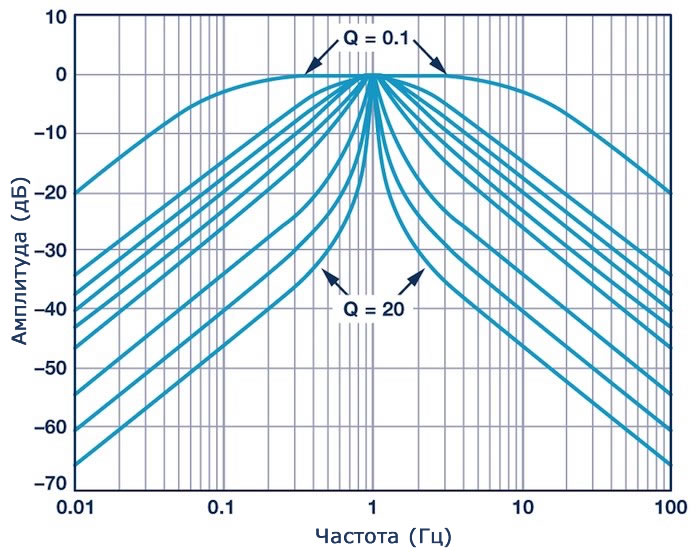
Еще одно преимущество – это то, что мы знаем из нашего опыта работы с фильтрами. Радиочастотные системы вращаются вокруг частот и различных способов генерации, управления или воздействия на эти частоты с помощью компонентов и паразитных элементов схемы. Шкала в дБ в подобном контексте удобна, потому что графики частотных характеристик интуитивно понятны и визуально информативны, когда ось частот использует логарифмический масштаб, а ось амплитуды использует шкалу в дБ.

Диаграмма Боде, показывающая амплитудно-частотные характеристики различных полосовых фильтров

Когда дБ абсолютны?

Мы установили, что дБ является отношением и, следовательно, не может описывать абсолютные значения мощности и амплитуды сигнала. Однако было бы неудобно постоянно переключаться между значениями в дБ и не в дБ, и, возможно, именно поэтому радиоинженеры ввели единицу измерения дБм (dBm).

Мы можем избежать проблемы «только отношение», просто создав новую единицу измерения, которая всегда будет содержать опорное значение. В случае дБм опорное значение равно 1 мВт. Таким образом, если у нас есть сигнал 5 мВт, и мы хотим оставаться в области дБ, мы можем выразить мощность этого сигнала как 7дБм:

\[10 \log_ <10>\left( < 5 мВт \over 1 мВт >\right) = 10 \log_ <10>(5) \approx 7 дБм\]

Вы определенно хотите ознакомиться с концепцией дБм. Это стандартная единица, используемая в реальной разработке радиочастотных систем, и она очень удобна, когда вы, например, вычисляете энергетический баланс линии связи, поскольку усиления и потери, выраженные в дБ, могут просто складываться и вычитаться из выходной мощности, выраженной в дБм.

Существует также единица дБВт (dBW); в качестве опорного значения она использует 1 Вт вместо 1 мВт. В настоящее время большинство радиоинженеров работает с относительно маломощными системами, и это, вероятно, объясняет, почему дБм встречается чаще.

Больше вариаций дБ

Две других единицы измерения, основанных на дБ, – это дБн (dBc) и дБи (dBi).

Вместо фиксированного значения, такого как 1 мВт, дБн (dBc) использует в качестве опорного сигнала уровень несущей сигнала. Например, фазовый шум (смотрите второй раздел данной главы) выражается в единицах дБн/Гц (dBc/Hz); первая часть этой единицы измерения указывает, что мощность фазового шума на определенной частоте измеряется относительно мощности несущей (в этом случае «несущая» относится к мощности сигнала на номинальной частоте).

Идеализированная точечная антенна принимает определенное количество энергии от схемы передатчика и равномерно излучает ее во всех направлениях. Считается, что эти «изотропные» антенны имеют нулевой коэффициент усиления и нулевые потери.

Однако, другие антенны могут быть сконструированы таким образом, чтобы концентрировать излучаемую энергию в определенных направлениях, и в этом смысле антенна может иметь «усиление». Антенна на самом деле не добавляет мощности к сигналу, но эффективно увеличивает переданную мощность путем концентрации электромагнитного излучения в соответствии с направлением системы связи (очевидно, что более практично, когда разработчик антенны знает пространственную взаимосвязь между передатчиком и приемником).

Здесь вы можете увидеть неравномерное распределение излучаемой энергии, которая приводит к усилению в прямом направлении (т.е., 0°)

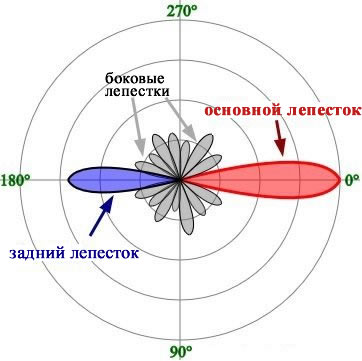
Единица измерения дБи (dBi) позволяет производителям антенн указывать «коэффициент усиления», который использует популярную шкалу дБ. Как всегда, когда мы работаем с дБ, нам необходимо отношение, а в случае с дБи (dBi) коэффициент усиления антенны выражается через опорное усиление изотропной антенны.

Некоторые антенны (например, те, которые сопровождаются параболическим зеркалом, «тарелкой») имеют значительный коэффициент усиления, и поэтому они могут внести нетривиальный вклад в расстояние и производительность радиочастотной системы.

Источник

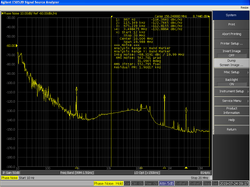
Фазовый шум в анализаторе спектра: как спуститься ниже –120 дБн/Гц на отстройке 10 кГц в диапазоне частот до 14 ГГц, или Борьба за децибелы

Что такое фазовый шум?

Фазовый шум— это один из важнейших
критериев оценки частотной стабильности
любого источника сигнала (генератора). Частотная стабильность генератора является качественным показателем того, насколько точно данный генератор может воспроизводить
одну и ту же выходную частоту в заданном
временном интервале. Любой источник сигнала (генератор) будет иметь определенную
стабильность (или, наоборот, нестабильность) генерации выходной частоты. Данная
стабильность бывает двух видов: долговременная и кратковременная. Долговременная
стабильность описывает флуктуации частоты, которые имеют место в течение длительного временного интервала: отношение ухода частоты к ее номинальному значению за
день, месяц, год. Кратковременная стабильность — это изменения в номинальном значении выходной частоты за временной промежуток, который измеряется секундами.

Математически идеальный синусоидальный сигнал описывается как:

где V₀ — номинальная амплитуда сигнала;
2πf₀t — величина, описывающая линейное
приращение фазы; f₀ — номинальная частота сигнала.

Однако реальный сигнал правильнее моделировать как (рис. 1):

где ε(t) — амплитудные флуктуации; Δφ(t) — флуктуации фазы.

Рис. 1. РЧ-сигналы в частотной и временной области:
а) идеальный сигнал V(t) = V0sin(2πf0t); б) реальный сигнал V(t) = [V0+ε(t)] sin[2πf0t+Δφ(t)]

Есть два типа фазовых флуктуаций — детерминированные и стохастические. Детерминированные флуктуации представляют собой
дискретные сигналы на определенных отстройках от несущей частоты. Эти сигналы могут быть четко соотнесены с определенными
факторами применительно к данному источнику сигнала, например, частота линии питания, частота вибрации, комбинационные продукты смешения. Стохастические флуктуации
имеют случайную природу, и именно их обычно называют фазовым шумом. Причиной таких флуктуаций является тепловой шум, дробовый шум ифликкер-шум в полупроводниковых элементах. Для количественной оценки
фазового шума источника используется оценка девиации частоты или фазы в частотной либо временной области. Поскольку между частотой и фазой существует четкая взаимосвязь,
то все термины, которые характеризуют флуктуации частоты и фазы (например, фазовый
шум и джиттер), также взаимосвязаны.

Фундаментальным определением фазового шума является спектральная плотность
мощности (СПМ) фазовых флуктуаций S_φ
в заданной полосе частот, данная величина
имеет размерность рад 2 /Гц:

где f_m — частота отстройки от несущей;
Δφ_СКЗ — среднеквадратическое значение
флуктуации фазы; BW— полоса, используемая при измерении Δφ_СКЗ.

Другим термином, который очень часто используется для характеристики фазового шума, является спектральная плотность мощности фазового шума в одиночной боковой полосе L(f_m). Данная величина связана с S_φ(f_m)
путем простой аппроксимации, которая верна при условии, что общая пиковая девиация
фазы оказывается много меньше, чем 1 рад:

Величина L(f_m) легче всего соотносится со
спектральным распределением мощности РЧ-и СВЧ-сигналов, которые мы обыкновенно
наблюдаем на анализаторе спектра. Согласно определению Международного института радиоинженеров (IEEE), спектральная
плотность мощности фазовых шумов в одиночной боковой полосе равна:

где P_SSB — спектральная плотность шума на
заданной отстройке от несущей в одиночной
боковой полосе, пересчитанная в полосу 1 Гц;
P_TOTAL — полная мощность сигнала.

Величина L(f_m) обыкновенно представляется в логарифмическом масштабе в децибелах относительно несущей (или относительно сигнала) на Гц (дБн/Гц или дБс/Гц).

При использовании L(f_m) следует помнить,
что данная величина служит корректным критерием оценки фазового шума, если выполняется правило «малого угла», то есть если пиковая девиация фазы ЧастотаСПМ фазового шума, дБн/Гцотстройка
100 Гцотстройка
1 кГцотстройка
10 кГцотстройка
100 кГцХороший уровень фазовых шумов
(генераторы Anritsu MG369xB,
Agilent PSG, Rohde & Schwarz SMF100A,
анализаторы спектра Agilent PSA, 8560EC, Advantest R3273,
Rohde & Schwarz FSEM30/FSEK30/ESIB26/ESIB40)Частота 4 ГГц–(90–95)–(110–115–(118–120)–(120–125)Частота 10 ГГц–(85–90)–(105–110)–(110–115)–(118–123)Сверхнизкий уровень фазовых шумов
(генераторы Agilent N5508A (70428A), Aeroflex FS5000,
анализаторы спектра Rohde & Schwarz
FSU/FSQ/FSUP/ESU/FSMR*)Частота 4 ГГц–(95–100)–(120–125)–(128–130)–(130–135)Частота 10 ГГц–(90–95)–(115–120)–(120–125)–(125–130)

Для понимания разницы в параметрах фазового шума генераторов и анализаторов спектра следует иметь в виду, что первые гетеродины анализаторов спектра при подаче на
вход частоты 1 ГГц обыкновенно настроены
на 4–5 ГГц (поскольку их первая ПЧ в диапазоне трехкратного преобразования всегда находится выше по частоте, чем сигнал РЧ).
Именно поэтому в диапазоне до 3–4 ГГц фазовые шумы синтезированного генератора
всегда лучше шумов анализатора спектра одного класса. На частотах выше 3–4 ГГц (там,
где анализаторы спектра используют ПЧ порядка 300–450 МГц и ЖИГ-фильтр для подавления зеркального канала) фазовые шумы анализатора спектра и генератора одного
класса обычно оказываются сопоставимыми.

Различные схемы построения
синтезированных генераторов
и гетеродинов с точки зрения
получения оптимальных
фазовых шумов

Каким образом могут быть получены низкие фазовые шумы? Какие схемы построения
следует признать оптимальными, а какие нет?
Мы попытаемся ответить на данные вопросы. При этом будем опираться на опыт анализа различных типов архитектур синтезированных генераторов (гетеродинов) ведущих зарубежных компаний, а также на опыт
разработки собственных малошумящих
и сверхмалошумящих синтезированных генераторов (гетеродинов), который был получен ЗАО ПФ «ЭЛВИРА» за десятилетие
производства различных моделей анализаторов спектра СК4-БЕЛАН.

Синтезированный гетеродин анализатора
спектра должен в идеале удовлетворять трем
требованиям:

Обыкновенно те же самые требования
предъявляются и к синтезированному генератору. Следует отметить, что теоретически
минимальные фазовые шумы и самую высокую скорость перестройки будут иметь генераторы, построенные на основе прямого аналогового синтеза. Однако решение задачи получения узкого шага по частоте и малых
комбинационных составляющих в синтезаторе, построенном по принципу прямого
синтеза, предполагает очень высокую конечную стоимость прибора. Для приложений,
когда нужна симуляция сверхчистых и сверхскоростных сигналов (то есть когда речь идет
о генераторе), высокая стоимость иногда оказывается, тем не менее, приемлемой. Если же
речь идет о построении первых гетеродинов
для анализаторов спектра, то от прямого аналогового синтеза, как правило, отказываются.
По крайней мере, коммерчески доступные
анализаторы спектра, имеющие в качестве гетеродина синтезатор, выполненный по принципу прямого синтеза, автору данной статьи
неизвестны. Классические схемы построения
гетеродина в анализаторе спектра подразумевают ту или иную комбинацию методов
косвенного и прямого цифрового синтеза.
Именно о таких схемах и об их оптимизации
и пойдет речь далее.

Традиционная архитектура анализатора
спектра представляет собой супергетеродинный приемник с трехкратным преобразованием частоты. При этом первый гетеродин — это гетеродин, перестраиваемый в достаточно широкой полосе частот, а второй и третий — генераторы на точку. Фазовые шумы
анализатора спектра будут определяться шумами этих трех гетеродинов. Достичь хороших фазовых шумов в генераторе на одну частотную точку, в принципе, не представляет особых сложностей. Гораздо более сложной и актуальной задачей является создание
первого гетеродина, то есть синтезированного генератора с перестройкой порядка нескольких гигагерц, высокой дискретностью
(доли герц) и низкими фазовыми шумами.
Кроме того, решение этой задачи является,
по сути, отправной точкой для создания измерительного синтезированного СВЧ-генератора. Итак, как же получить искомые параметры в перестраиваемом синтезированном генераторе?

Сердцем любого синтезированного гетеродина является генератор, перестраивающийся
в широкой полосе частот (обычно в пределах
октавы, иногда до трех октав). До недавнего
времени этому требованию удовлетворяли генераторы с перестройкой на железо-иттриевом гранате, в последнее время появились
и широкополосные ГУНы (генераторы, управляемые напряжением) с октавной полосой перестройки, эквивалентной диапазону ЖИГ-генераторов или приближающейся к нему.

В концептуальном виде ядро СВЧ-генератора представлено на рис. 6.

Рис. 6. Ядро генератора

СПМ фазовых шумов в одиночной боковой полосе СВЧ-генератора может быть определена следующей формулой:

где G— коэффициент усиления активного элемента; F — фактор шума активного элемента;
k — постоянная Больцмана 1,38×10 –23 Дж/К;
t — температура; P — мощность, рассеиваемая на резонаторе; Q — нагруженная добротность резонатора; f₀ — номинальная выходная частота; f_a — частота отстройки, где начинается фликкер-ЧМ активного элемента;
f — частота отстройки.

Рис. 7. Схематичное представление фазовых шумов генератора

Из анализа формулы (16) становится очевидным, какие преимущества схемы синтезаторов на основе ЖИГ-генераторов имеют
по сравнению со схемами на основе ГУНов.
Поскольку ЖИГ-генераторы могут иметь добротность до 4000 на частоте 10 ГГц (по сравнению с добротностью от 30 до 300 у ГУНов
на более низких частотах 4–5 ГГц), то очевидно, что их фазовые шумы будут лучше на порядок. Некоторые ЖИГ-генераторы, разработанные в последние годы и использующие
в качестве активных элементов кремниевые
биполярные транзисторы, имеют фазовые
шумы на отстройке 100 кГц от несущей 18 ГГц
в –130 дБн/Гц (!), которые при смещении в зону дальних отстроек продолжают уменьшаться в соотношении 25 дБ на декаду. Данный
параметр пока недостижим для широкополосных ГУНов, лучшие из которых имеют
фазовый шум в –105 дБн/Гц на отстройке
100 кГц от несущей 4–5 ГГц. Следует помнить,
что ЖИГ-генераторы обыкновенно имеют
хорошие шумы на отстройках более 100 кГц
от несущей, ГУНы с аналогичной перестройкой удовлетворительные шумы имеют на отстройках более 500 кГц— 1 МГц от несущей.
Вблизи несущей (отстройки менее 100 кГц)
фазовые шумы оказываются неудовлетворительными как у ЖИГов, так и ГУНов, а их частотная нестабильность может достигать нескольких мегагерц (у ГУНов десятки мегагерц) для несущих порядка 4–5 ГГц. Это
означает, что для построения синтезированного гетеродина с узким шагом ЖИГ-генератор или ГУН нужно стабилизировать при помощи системы ФАПЧ. Простейшая схема — это однопетлевой синтезатор с ФАПЧ. Типичный однопетлевой синтезатор ФАПЧ включает в себя перестраиваемый генератор —
ГУН или ЖИГ-генератор, сигнал которого
после требуемого снижения по частоте подается на один из входов фазового детектора,
как показано на рис. 8.

Рис. 8. Простейший однопетлевой синтезатор

На другой вход фазового детектора подается опорный сигнал. Данный сигнал может
быть фиксированной частоты (в этом случае
используется делитель с переменным коэффициентом деления), или он может перестраиваться в некоторой (более узкой по сравнению с диапазоном ЖИГ-генератора или
ГУНа) полосе частот с высокой дискретностью. В последнем случае используется делитель с фиксированным коэффициентом деления. В первом случае разрешение по частоте нашего синтезированного генератора будет
определять частота фиксированного опорного сигнала, во втором случае — шаг перестраиваемого опорного генератора, помноженный на фиксированный коэффициент деления. Фазовый детектор сравнивает сигналы
на обоих входах и генерирует сигнал ошибки, который после фильтрации и усиления
(при необходимости) подстраивает частоту
ЖИГ/ГУН к f = F_REF×N, где F_REF — частота
опорного сигнала на входе фазового детектора. Главным преимуществом любой схемы на
основе ФАПЧ является более чистый спектр
выходного сигнала. Результирующий фазовый шум синтезатора в пределах полосы пропускания фильтра ФАПЧ равен:

Рис. 9. Формирование фазовых шумов в синтезаторе с ФАПЧ

На рис. 9 видно, что изначально ЖИГ-генератор и ГУН будут иметь оптимальные
петли ФАПЧ разной ширины (оптимальная
петля ГУН всегда шире). Область, закрашенная оранжевым цветом, — это та зона, где
ГУН всегда будет проигрывать ЖИГ-генератору при опорах со спектром одинаковой
чистоты. Таким образом, можно утверждать,
что наименьшие фазовые шумы в синтезаторе ФАПЧ для одинаковой опоры могут
быть получены на основе ЖИГ-генератора.
Синтезаторы на основе ГУН предпочтительнее в тех случаях, где ключевыми параметрами являются скорость перестройки и малое потребление. Неслучайно, что в последнее время стали появляться синтезаторы на
основе ГУНов, например Agilent N5183A или
Anritsu MG37022A. Однако применительно
к классу таких измерительных приборов,
как анализаторы спектра СВЧ-диапазона,
надо помнить о том, что скорость перестройки первого гетеродина является не последним ограничителем скорости: для подавления зеркального канала в СВЧ анализаторе спектра обычно используется ЖИГ-фильтр, который будет иметь скорость
перестройки, характерную для структур, работающих на основе ферромагнитного резонанса, то есть для ЖИГ-генератора. Иными словами, в анализаторе спектра СВЧ-диапазона использование ГУНа ухудшит
фазовые шумы, но в конечном счете не увеличит скорость. Это, правда, не касается тех
анализаторов, которые используют только
трехкратное преобразование по частоте.
Для таких анализаторов спектра использование ГУНа может привести к увеличению
скорости, а использование чистой опоры
позволит добиться сбалансированных параметров по фазовому шуму. Недостаток
таких анализаторов — это их ограниченный
частотный диапазон, как правило, не более
8 ГГц, обусловленный необходимостью увеличивать частоту первой ПЧ. Повторим, что
при одинаковой сложности схемы с точки
зрения фазовых шумов схемы на ЖИГ-генераторе всегда будут выигрышными. Поэтому говорить, в основном, мы будем
именно о них.

Приведенная на рис. 8 схема используется
в бюджетном анализаторе спектра СК4-БЕЛАН
(9 кГц – 2,2 ГГц). Первый гетеродин СК4-БЕЛАН
(ЖИГ-генератор, перестраиваемый в полосе
частот 2450–4650 МГц) делится на 256 до частот 9,57–18,16 МГц и подается на фазовый
детектор. На другой вход фазового детектора заводится опорный сигнал с синтезатора
прямого синтеза (DDS AD9850), перестраиваемого с шагом 0,01 Гц в тех же пределах.
В результате мы получаем синтезированный
гетеродин, перестраиваемый с шагом 10 Гц
(данная величина взята с запасом) в диапазоне частот 2,45–4,65 ГГц. Какие недостатки
есть у данной схемы? Первый недостаток очевиден: из-за использования высокого коэффициента деления со значением 256 шумы
в петле возрастают на 48 дБ относительно шумов L(f_m)_PD. Кроме того, шумы L(f_m)_PD не оптимизированы (выбраны бюджетный частотно-фазовый детектор (ЧФД) и делитель, синтезатор прямого синтеза (DDS) тактируется не
самым чистым сигналом), в результате чего
мы имеем в петле фазовый шум в –65 дБн/Гц.
Поэтому петля в СК4-БЕЛАН выбирается узкой, для того чтобы определяющими шумами для отстроек 10 кГц и далее являлись шумы ЖИГ-генератора (а на отстройке 10 кГц
шумы ЖИГ-генератора оставляют желать
лучшего). Данное решение, кроме того, продиктовано и тем соображением, что синтезатор прямого синтеза DDS при перестройке
в указанном диапазоне частот имеет случайные дискретные составляющие (spurious)
на уровне –80 дБ. В петле эти составляющие
умножаются на 20logN и возрастут на 48 дБ.
Поэтому петлю целесообразно делать узкой,
чтобы ослабить дискретные паразитные отклики фильтром низких частот петли ФАПЧ.
Подчеркнем, что описанное решение не является оптимальным с точки зрения фазовых
шумов и рассчитано на пользователей, которым нужен бюджетный анализатор спектра
со скромными параметрами.

Из изложенного выше видно, что ставить
делитель в петле — отнюдь не самое грамотное решение. Каким же другим способом
можно захватить ЖИГ-генератор? Наиболее
грамотное решение заключается в использовании для построения первого гетеродина
комбинации смешения и системы ФАПЧ
(рис. 10). Все анализаторы спектра с хорошими характеристиками фазовых шумов используют данный принцип. Рассмотрим данное решение более подробно на примере частотного синтеза в СК4-БЕЛАН 32 с опцией
003 (улучшенные фазовые шумы).

Рис. 10. Схема на основе комбинации смешения и ФАПЧ

Предположим, что у нас есть ЖИГ-генератор, настроенный на частоту 5 ГГц и дрейфующий в пределах 1 МГц (то есть частоту
которого мы можем выставить в пределах
±500 кГц). Если присутствует чистый сигнал
на частоте, например, 5,01 ГГц, то, подав данный сигнал на РЧ-вход смесителя, а сигнал
ЖИГ-генератора на его гетеродинный (LO)
вход, на выходе ПЧ-смесителя получим разностную частоту 10 МГц (данная величина
выбирается разработчиком). Затем данная
частота может быть подана на один из входов ЧФД, на другой вход можно будет подать
ту же самую частоту, например, с синтезатора
прямого синтеза, используемого в качестве
опоры. ЧФД станет вырабатывать сигнал
ошибки, который будет подстраивать ЖИГ-генератор по частоте и фазе. Откуда же взять
спектрально чистый сигнал на частоте 5,01 ГГц?
Не будем забывать и о том, что данный сигнал нам необходимо иметь во всем диапазоне частот ЖИГ-генератора, пусть и с грубым
шагом. Выход — использование генератора
гармоник, который даст грубую сетку опорных частот. Генератор гармоник — это устройство, как правило, реализуемое на основе
диода с накоплением заряда. На вход данного устройства подается полуволновой синус
высокой мощности (порядка 500–650 мВт),
а на выходе мы имеем спектр гармоник вида sinx/x, где первый ноль будет определяться длительностью импульса (чем короче импульс, тем более широкий диапазон перекрывается гармониками с равномерным
коэффициентом передачи). Перестраивая
ЖИГ-генератор, мы будем «бежать» по гармоникам, полученным при помощи генератора гармоник, выделять разностную частоту и захватывать с ее помощью ЖИГ-генератор. Расстояние по частоте от одной
гармоники до другой будем перекрывать, варьируя частоту опорного генератора, который сравнивается с разностной частотой. Это
связано с тем, что, изменяя частоту DDS, который в качестве опорного сигнала подается на ЧФД, мы перестраиваем и захваченный
ЖИГ-генератор. При этом шаг перестройки
ЖИГ-генератора определяется минимальным шагом синтезатора прямого синтеза
(для современных DDS это тысячные доли
герца), а полоса такой перестройки — диапазоном рабочих частот DDS. Следует отметить, что полосу перестройки DDS необходимо ограничивать, для того чтобы избежать
попадания на фазовый детектор случайных
дискретных составляющих, которые имеют
максимальный уровень на частотах, кратных
тактовой (1/2, 1/3, 1/4, 1/8).

Отсюда следуют несколько выводов:

Диапазон частот перестройки такого генератора нужно выбирать следующим образом: гармоника n от конечной частоты ГУНа
должна быть выше по частоте гармоники n+1
от начальной частоты ГУНа.

Пример: в СК4-БЕЛАН 32 ЖИГ-генератор
перестраивается от 4421,4 до 7621,4 МГц.
На умножитель для формирования грубой сетки частот подается сигнал с ГУНа 400–440 МГц
с шагом 1 МГц. В начале диапазона частот
ЖИГ-генератора мы работаем по 11-й гармонике. Когда подаем на вход умножителя последнюю частоту ГУНа 440 МГц, то получаем гармонику на частоте 4840 МГц. Затем переходим на 12-ю гармонику и при подаче на
умножитель первой частоты ГУНа 400 МГц
получаем 4800 МГц. В результате диапазоны,
перекрываемые 11-й гармоникой от 440 МГц
и 12-й от 400 МГц, накладываются или «сшиваются», и мы получаем сетку частот без пропусков, где шаг между гармониками меняется от 11 до 18 МГц. Как нетрудно заметить,
расстояние в 11–18 МГц легко перекрыть при
помощи DDS без значительных случайных
дискретных составляющих. Обращаем внимание, что чем выше номер гармоники, тем
шире будет участок наложения гармоник.
А вот если бы мы выбрали последней частотой ГУНа, например, 420 МГц, то на 11-й
гармонике могли бы дойти только до частоты 4620 МГц, 12-я гармоника от 400 МГц
давала бы те же 4800 МГц, а в частотном диапазоне образовалась бы «дыра» в 180 МГц,
где бы не было захвата ЖИГ-генератора,
поскольку диапазон в 180 МГц пройти с узким шагом на DDS без «спуров» в диапазоне от –45 до 50 дБн не представляется возможным.

Итак, архитектура первого синтезированного гетеродина в анализаторе спектра с малыми шумами нам теперь ясна:

Какие же эффективные фазовые шумы
получаются в анализаторе при использовании частотного синтеза на основе косвенного синтеза с ФАПЧ, описанного выше? Рассмотрим фазовые шумы всех гетеродинов
прибора. Первый гетеродин СК4-БЕЛАН 32
с опцией 003 имеет фазовый шум, показанный на рис. 11.

Рис. 11. Фазовый шум первого гетеродина СК4-БЕЛАН 32/003 на частоте 4521,4 МГц
(соответствует входной частоте 100 МГц на анализаторе)

Второй гетеродин СК4-БЕЛАН 32/003 имеет частоту 4 ГГц и фазовый шум, показанный
на рис. 12.

Источник