Декартово произведение что это
Декартово (прямое) произведение множеств
ДЕКАРТОВО ПРОИЗВЕДЕНИЕ МНОЖЕСТВ. СООТВЕТСТВИЯ, ФУНКЦИИ, ОТНОШЕНИЯ
ЦЕЛЬ ЛЕКЦИИ – изучение свойств декартова произведения множеств, и связанных с ним соответствий, функций и отношений.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Помимо рассмотренных в первой лекции традиционных операций над множествами существуют и другие действия с множествами, которые позволяют решать много задач, имеющих практическое применение. В частности, к таким действиям относится декартово (прямое) произведение множеств. Свое название декартово произведение получило оттого, что предложенное Декартом координатное представление точек плоскости, являлось исторически первым примером прямого произведения.
Декартово (прямое) произведение множеств
Декартово (прямое) произведение множеств Х и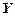 
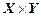
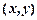
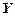
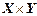
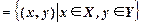
– это множество, обозначаемое 
, элементами которого являются упорядоченные пары 
, первая компонента которых принадлежит множеству Х, а вторая множеству .
.
Согласно определению элементами прямого произведения множеств являются упорядоченные пары, составленные из элементов исходных множеств. В этих парах первый элемент (компонента) всегда принадлежит первому множеству, а второй элемент (компонента) второму. Порядок множеств определяется исходной записью и, если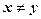 
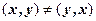
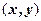
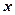
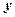
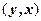
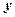
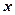
, то 
, так как в упорядоченной паре 
компонента 
имеет номер 1, а компонента 
– номер 2, но в упорядоченной паре 
: – номер 1, а – номер 2.
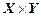
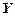
Множество содержит mn элементов, где m и n – количество элементов Хи соответственно.
Геометрическое представление этого множества приведено на рис. 2.1, а.
Пример 2.2. Пусть A и B – отрезки вещественной оси. Прямое произведение изобразится заштрихованным прямоугольником, показанным на рис. 2.1, б.
Пример 2.3. Найти декартово произведение множеств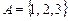 
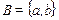
и 
.
Решение. A × B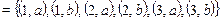 
.
Порядок перечисления элементов безразличен, важен только порядок элементов в паре (упорядоченная пара).
B × A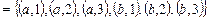 
.
Из приведенных примеров видно, что свойства прямого произведения отличаются от свойств обычного произведения в арифметическом смысле. В частности, прямое произведение изменяется при изменении порядка сомножителей, то есть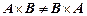 
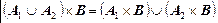
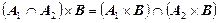
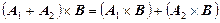
, следовательно, декартово произведение не коммутативно. При этом он не только не коммутативно, но и не ассоциативно, но дистрибутивно относительно объединения, пересечения и симметрической разности множеств
;
;
.
Прямое произведение множеств – операция многоместная
.
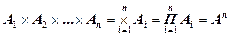
В результате получаются множества, состоящие из упорядоченной последовательности вида
, где 
; 
;…; 
.
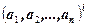
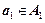
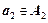
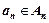
Такие последовательности называются кортежами или векторами.
Кортеж длины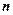 
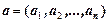
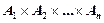
– конечная последовательность элементов 
, в которой каждый элемент занимает определенное место в соответствии с записью исходных множеств 
декартова произведения.
Сами элементы при этом называются компонентами (координатами) кортежа, которые нумеруются слева направо (первая компонента, вторая компонента и т.д.).
Примеры кортежей: множество людей, стоящих в очереди, числа, выражающие координаты точки на плоскости и т.п. Во всех этих множествах место каждого элемента является вполне определенным и не может быть произвольно изменено.
Основные отличия понятий кортежа (вектора) и множества заключаются в следующем:
1) в множестве порядок элементов не играет роли, а кортежи, отличающиеся порядком элементов, различны, даже в случае, когда они имеют одинаковый состав;
2) в множестве все элементы различны, а в кортеже координаты могут повторяться.
Таким образом, в отличии от обычного множества в кортеже (векторе) могут быть одинаковые компоненты: два одинаковых слова в фразе, одинаковые численные значения координат точки на плоскости и т.п.
Таким образом, декартово произведение позволяет получать вектора любых размерностей. Эта операция отличается от операций объединения и пересечения тем, что в результате перемножения прямым способом получаются объекты, содержащие элементы, отличающиеся по своей природе от элементов исходных множеств.
Если перемножить n раз одно и то же множество, то получится множество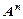 
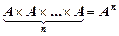
, называемое степенью множества
.
Степенью декартового произведения называется число множеств n, входящих в это декартово произведение.
Поиск декартова произведения с помощью LINQ
Постановка вопроса: как найти декартово произведение произвольного количества последовательностей с помощью LINQ?
С помощью LINQ вы можете составить декартово произведение любого количества последовательностей достаточно просто, если вы изначально знаете, с каким количеством будете работать:
public static IEnumerable IEnumerable T >> CartesianProduct T > ( this IEnumerable IEnumerable T >> sequences )
Что ж, есть причина использовать индукцию; эта идея практически никогда не подводит при работе с рекурсивно определенными структурами данных.
from old in oldProduct
from item in sequence
И теперь у нас есть благополучный индукционный переход. Если oldProduct — любое декартово произведение, то мы можем вычислить его комбинацию с другой последовательностью, чтобы получить новое декартово произведение.
Давайте соберем все это вместе:
static IEnumerable IEnumerable T >> CartesianProduct T > ( this IEnumerable IEnumerable T >> sequences )
IEnumerable IEnumerable T >> result = new [ ] < Enumerable. Empty T >( ) > ;
foreach ( var sequence in sequences )
var s = sequence ; // нельзя замыкаться на переменную цикла
// индукционный переход: используем SelectMany, чтобы построить новое произведение из старого
from seq in result
select seq. Concat ( new [ ] < item >) ;
В данном случае мы начнем с пустым произведением в качестве аккумулятора, и каждый раз мы будем «добавлять» к нему путем комбинирования текущей последовательности с произведением предыдущих. На каждом шаге алгоритма, аккумулятор равен декартовому произведению уже просмотренных последовательностей.
static IEnumerable IEnumerable T >> CartesianProduct T > ( this IEnumerable IEnumerable T >> sequences )
IEnumerable IEnumerable T >> emptyProduct = new [ ] < Enumerable. Empty T >( ) > ;
return sequences. Aggregate (
from accseq in accumulator
from item in sequence
select accseq. Concat ( new [ ] < item >) ) ;
И напоследок несколько слов для разбирающихся. Помните, результат LINQ-запроса есть запрос, который предоставит результаты по требованию, а не результаты непосредственно. Когда мы строим этот аккумулятор, мы вообще-то не вычисляем декартово произведение. Мы строим большой сложный запрос, который при запуске выдаст декартово произведение. Запрос строится энергично, но выполняться будет лениво.
От переводчика
Эрик обошел в своем посте конкретное название идиомы, которую он использовал, а именно свертки. Впрочем, на эту тему на Хабрахабре уже были посты. Интересующийся может найти отличный перевод «Катаморфизм в F#».
В сумме свертка, пайплайны и списочные выражения дадут вот такой красивый код:
Лекция 2. Декартово произведение. Мощность множества
п.2. Декартово произведение. Мощность множества.
2.1. Декартово произведение множеств.
Упорядоченная пара 
интуитивно определяется как совокупность, состоящая из двух элементов x и y, расположенных в определенном порядке. Две пары 
и 
считаются равными тогда и только тогда, когда x=u и y=v.
Определение 2.1. Пусть A и B – два множества. Прямым (декартовым) произведением двух множеств A и B называется множество всех упорядоченных пар, в котором первый элемент каждой пары принадлежит A, а второй принадлежит B:
Пример. Пусть 
и 
. Тогда
.
.
Пример. На координатной плоскости построить следующее множество:
Решение. Первое множество помещаем на оси OX, второе на оси OY. Множество всех пар, т. е. декартово произведение, изображается точками заштрихованного прямоугольника, но без левой и нижней стороны.
. Метод координат ввел в употребление Рене Декарт (), отсюда и название «декартово произведение».
.
.
и вообще 
.
( 
– первая буква древнееврейского алфавита, называемая «алеф», символ 
читается: «алеф-нуль»). В частности |N|=
.
. Следующую теорему примем без доказательства.
– конечные попарно непересекающиеся множества, т. е. 
. Тогда
(2.3.1.)
. Тогда
(2.3.2.)
и множества S1, S2 и S3 попарно непересекающиеся, то
.
, которые могут иметь непустые пересечения между собой, т. е. объединение может быть не разбиением. В общем случае имеет место следующая теорема, которую нетрудно доказать методом математической индукции. 
, справедлива формула включений и исключений.
(2.3.3.)
.
.
.
.
.
. Множество X1ÇX3 – множество положительных целых чисел, которые делятся на 2 или 5. Число элементов или мощность этого множества равно 
. Множество X2ÇX3 – множество положительных целых чисел, которые делятся на 3 или 5. Число элементов или мощность этого множества равно 
.
.
. Элементы универсума нумеруются:
– это i-й разряд кода C.