Десятичная система исчисления что это
Десятичная система счисления
Система счисления — это способ записи (представление) чисел с помощью определённого набора письменных знаков.
Десятичная система счисления — это позиционная система счисления, в которой для записи чисел используют десять знаков:
1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Знаки, употребляемые для записи чисел, называются цифрами.
В десятичной системе значение одной и той же цифры зависит от её позиции в записи числа. Для примера возьмём число 777, которое состоит из трёх одинаковых цифр. В этом числе первая слева цифра означает семь сотен, вторая — семь десятков, а третья — семь единиц. Так как значение цифры зависит от её позиции в записи числа, десятичную систему счисления также называют позиционной.
Позиционной называют такую систему счисления, в которой значение цифры зависит от её позиции в записи числа.
Числа, которые записаны с помощью одной цифры, называют однозначными, записанные с помощью двух — двузначными, так же по количеству цифр в числе дают названия и другим числам:
Однозначные числа: 1, 2, 4.
Двузначные числа: 14, 77, 92.
Трёхзначные числа: 122, 345.
Шестизначные числа: 537633, 987345.
Двузначные, трёхзначные, четырёхзначные, пятизначные и т. д. числа называют многозначными.
Следует помнить, что цифра и число не одно и то же.
Цифра – это только письменный знак, используемый для записи числа. Число может быть обозначено не одной, а несколькими цифрами (например, 75) или может быть выражено словами (семьдесят пять).
Системы счисления. Позиционная система счисления десятичная.
Впервые позиционная система счисления возникла в древнем Вавилоне. В Индии система работает в
виде позиционной десятичной нумерации с использованием нуля, у индусов данную систему чисел
позаимствовала арабская нация, у них, в свою очередь, взяли европейцы. В Европе эту систему стали
Позиционная система счисления — значение всех цифр зависит от позиции (разряда) данной цифры в числе.
Примеры, стандартная 10-я система счисления – это позиционная система. Допустим дано число 453.
Цифра 4 обозначает сотни и соответствует числу 400, 5 — кол-во десятков и соответствует значению 50,
а 3 — единицы и значению 3. Легко заметить, что с увеличением разряда увеличивается значение. Таким
образом, заданное число запишем в виде суммы 400+50+3=453.
Десятичная система счисления.
Здесь 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, однако информативная нагрузка не лишь у цифры, но и у места,
на котором цифра стоит (то есть ее позиция). Первая цифра числа справа указывает на единицы, вторая
33310 = 3*100 + 3*10+3*1 = 300 + 30 + 3
Десятичная позиционная система счисления является наиболее распространенной из всех систем. Конкретно ею мы
пользуемся, называя цену товара или номер автобуса. Во всех разрядах (позициях) можно использовать лишь одну цифру
от 0 до 9. Основание позиционной системы счисления – это число 10.
Один десятичный разряд в десятичной системе счисления бывает называют декадой. В цифровой электронике одному
десятичному разряду десятичной системы счисления соответствует один десятичный триггер.
Позиционные системы счисления арифметические операции.
Таблица сложения в десятичной системе счисления.
Основные сведения о десятичной системе счисления
Системы счисления. Основные понятия
Система счисления — это набор правил записи чисел посредством конечного набора цифр.
Системы счисления разделяются на:
Основание системы счисления — это количество цифр, используемых в данной системе.
Вес разряда — это отношение количественного эквивалента цифры в данном разряде к количественному эквиваленту такой же цифры в нулевом разряде:
Разряды числа нумеруются справа налево. Младший разряд имеет номер ноль. Разряды дробной части нумеруются отрицательными числами:
Что такое десятичная система счисления
Десятичная система счисления — это система счисления по целочисленному основанию 10 (0,1,2,3,4,5,6,7,8,9 арабские цифры). Она является позиционной системой счисления и наиболее распространенной.
Ученые утверждают, что использование такой распространенной системы связана с количеством пальцев на руках у человека.
Десятичные цифры используют в двоично-десятичном кодировании в двоичных компьютерах.
Алгоритм перевода чисел из любой системы счисления в десятичную
Перевести целое число с основанием q в десятичное можно с помощью следующего алгоритма:
Также можно переводить дроби с основанием q в десятичную систему счисления. Воспользуемся следующей формулой:
Примеры решения задач
Дано число в двоичной система 10011. Перевести число в десятичную систему счисления.
10011 2 = 1 ∙ 2 4 + 0 ∙ 2 3 + 0 ∙ 2 2 + 1 ∙ 2 1 + 1 ∙ 2 0 = 1 ∙ 16 + 0 ∙ 8 + 0 ∙ 4 + 1 ∙ 2 + 1 ∙ 1 = 16 + 0 + 0 + 2 + 1 = 19 10
Перевести в десятичную систему счисления число 17 из восьмеричной системы.
17 8 = 1 ∙ 8 1 + 7 ∙ 8 0 = 1 ∙ 8 + 7 ∙ 1 = 8 + 7 = 15 10
Перевести из пятеричной системы счисления число 20341 в десятичную систему.
20341 5 = 2 ∙ 5 4 + 0 ∙ 5 3 + 3 ∙ 5 2 + 4 ∙ 5 1 + 1 ∙ 5 0 = 2 ∙ 625 + 0 ∙ 125 + 3 ∙ 25 + 4 ∙ 5 + 1 ∙ 1 = 1250 + 0 + 75 + 20 + 1 = 1346 10
Число 0,F3D0 из шестнадцатеричной системы счисления перевести в десятичную систему.
Перевести в десятичную систему счисления двоичное число 101,11.
Десятичная система счисления

Всего получено оценок: 199.
Всего получено оценок: 199.
Все вычисления в математике выполняются в позиционной десятичной системе счисления. Кратко об особенностях десятичной системы можно прочитать в данной статье.
Что такое десятичная система счисления
В десятичной системе для представления чисел использует десять арабских цифр от 0 до 9, соответственно основанием десятичной системы счисления является число 10.
Историки, изучающие культуру древнего востока, в Индии обнаружили плиту с начертанием числа в позиционной десятичной системе. Возраст найденного артефакта составляет порядка 1,5 тысяч лет. Здесь же в древней Индии впервые используется ноль, как самостоятельная цифра.
Развернутая форма представления десятичного числа
Важным понятием в позиционном подходе представления чисел является понятие разряда. Различают разряды единиц, десятков, сотен, тысяч и так далее. Любое десятичное число можно представить, в так называемом развернутом виде, когда число записывается в виде суммы разрядных слагаемых, представленных в виде произведения значащей цифры разряда и числа десять в степени соответствующего разряда.
Например, десятичное число 46758 в развернутом виде будет выглядеть следующим образом:
46758 = 4 * 10^4 + 6 * 10^3 + 7 * 10^2 + 5 * 10^1 + 8 * 10^0
46758 = 4 * 10000 + 6 * 1000 + 7 * 100 + 5 * 10 + 8 * 1
Прямой перевод числа из десятичной системы
Перевод целого десятичного числа в какую-либо систему счисления выполняется путем поочередного деления самого числового значения, а затем полученных частных на основание системы счисления, в которую производится перевод.
Например, для перевода десятичного числа в двоичную систему выполняют деление на два, в восьмеричную – на восемь, в шестнадцатеричную – на шестнадцать. В принципе, десятичное число можно перевести и в пятеричную и семеричную системы, выполнив деление на пять или семь.
Выполнив первый шаг деления на, например, два, остаток запоминают, а полученное частное снова делят на основание. Эту операцию выполняют до тех пор, пока последнее частное не будет меньше или равно делителю.
Записывать сформированное число в новой системе счисления необходимо начиная с итогового частного и затем друг за другом выписывая остатки от деления от последнего к первому.
Например, прямой перевод числа 27 из десятичной системы в двоичную выполняют так:
27 / 2 = 13 и остаток 1
13 / 2 = 6 и остаток 1
6 / 2 = 3 и остаток 0
3 / 2 = 1 и остаток 1
Таким образом, 27 в двоичном формате это число 11011.
Для перевода чисел в пределах можно пользоваться таблицей соответствия десятичных и двоичных чисел
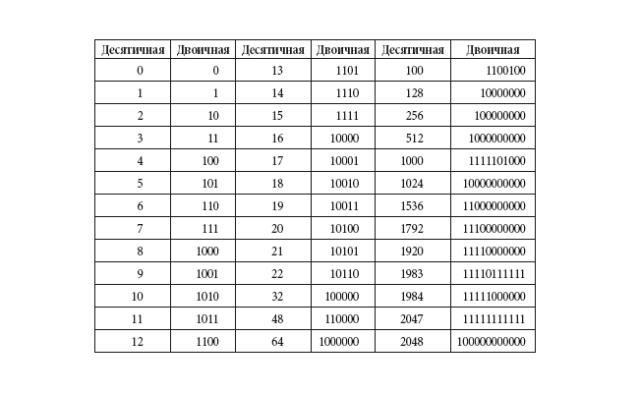
Обратный перевод числа в десятичную систему
Для перевода чисел в десятичную систему удобно пользоваться развернутой формой. При этом числовые значения записываются в виде суммы произведений цифр разрядов на основание текущей системы счисления в степени разряда.
Например, двоичное число 11011 можно представить так:
1 * 2^4 + 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 1 * 2^0 = 1 * 16 + 1 * 8 + 0 * 4 + 1 * 2 + 1 * 1 =27
Для упрощения вычислений удобно пользоваться таблицей степени двойки
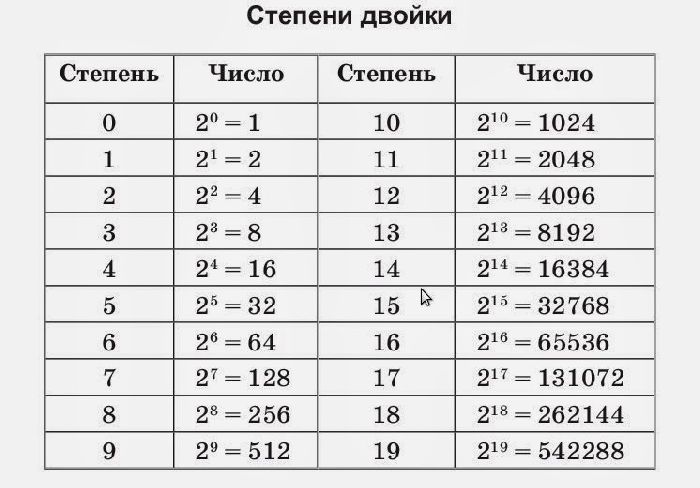
Что мы узнали?
В десятичной позиционной системе для представления числовых значений используются десять арабских цифр. Числа в такой системе можно представлять в развернутом виде. Перевод десятичных чисел в другую систему выполняется путем поочередного деления на основание новой системы счисления. Обратный перевод удобно выполнять с использованием развернутой формы записи числа.
СОДЕРЖАНИЕ
Источник
Десятичная запись
Для представления неотрицательного числа десятичное число состоит из
Десятичные дроби
Отсюда следует, что число является десятичной дробью тогда и только тогда, когда оно имеет конечное десятичное представление.
Приближение действительных чисел
Бесконечное десятичное разложение
Рациональное число
Верно и обратное: если в какой-то момент десятичного представления числа одна и та же последовательность цифр начинает повторяться бесконечно, число является рациональным.
Десятичное вычисление
Однако для большинства целей двоичные значения преобразуются в эквивалентные десятичные значения или из них для представления или ввода от человека; компьютерные программы по умолчанию выражают литералы в десятичном виде. (Например, 123.1 записывается как таковая в компьютерной программе, хотя многие компьютерные языки не могут точно закодировать это число.)
История
История десятичных дробей
Десятичные дроби были впервые разработаны и использованы китайцами в конце 4 века до нашей эры, а затем распространились на Ближний Восток, а оттуда в Европу. Письменные китайские десятичные дроби были непозиционными. Однако подсчет долей стержней был позиционным.
寸 





Предшественник современной европейской десятичной системы счисления был введен Симоном Стевином в 16 веке.
Естественные языки
В Индии появился метод выражения всех возможных натуральных чисел с помощью набора из десяти символов. В некоторых индийских языках используется простая десятичная система. Многие индоарийские и дравидийские языки имеют числа от 10 до 20, выраженные в регулярном порядке прибавления к 10.
В венгерском языке также используется простая десятичная система. Все числа от 10 до 20 образуются регулярно (например, 11 выражается как «tizenegy» буквально «один на десять»), как и числа от 20 до 100 (23 как «huszonhárom» = «три на двадцать»).
Некоторые психологи предполагают, что неправильные английские названия цифр могут затруднять счет детей.
Другие базы
В некоторых культурах используются или использовались другие системы исчисления.






