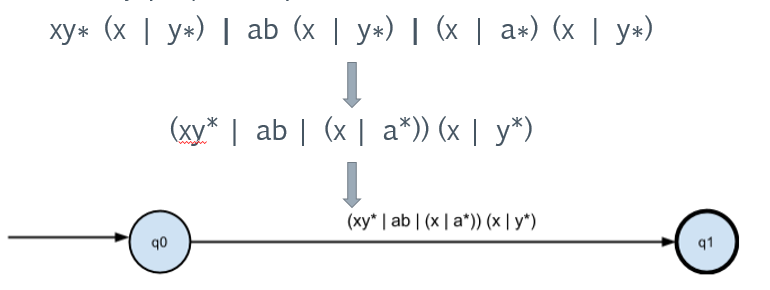Детерминированный и недетерминированный конечный автомат в чем разница
Детерминированный и недетерминированный конечный автомат в чем разница
Конечный автомат — абстрактная модель, типичный паттерн в разработке компиляторов и не только. Реализовать автомат можно в любом стиле программирования — процедурном, объектно-ориентированном или функциональном.
Что такое автомат?
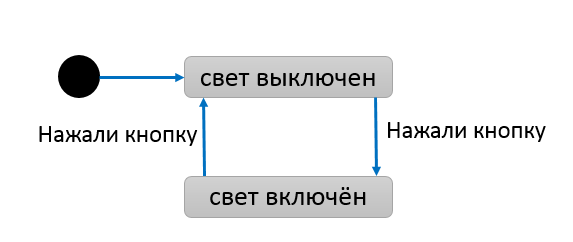
Будучи абстрактной моделью, автомат в коде или в схемах может стать чем угодно. Ниже показан пример диаграммы состояний для автомата, моделирующего выключатель:
У этого автомата есть:
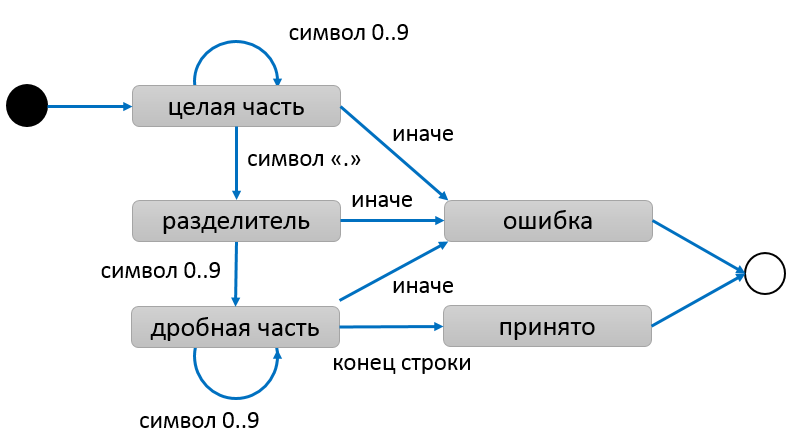
Чуть более сложный автомат для разбора числа с плавающей точкой показан ниже:
Оба этих автомата являются детерминированными, потому что входной символ или событие однозначно определяет переход, и нет “самопроизвольных” переходов при отсутствии события. Если эти условия не соблюдаются, автомат становится недетерминированным. Также автомат не является детерминированным, если он использует дополнительную память (например, стек ранее накопленных символов) для принятия решения о переходе.
Детерминированный и недетерминированный конечные автоматы
Детерминированный конечный автомат может разобрать строку в один проход из начала в конец, не используя дополнительной памяти кроме заранее заданных таблицы состояний и таблицы переходов между состояниями по событиям. В этой предсказуемости и линейной сложности разбора строки его главное преимущество. Например, в конце разбора строки автомат лексического анализатора приходит в состояние accepted либо в состояние error, что означает успешный или неуспешный разбор строки на токены соответственно.
Любой детерминированный конечный автомат имеет эквивалентное регулярное выражение, и эквивалетный язык регулярной грамматики, и наоборот. По сути это три разных формы представления одной сущности.
Существует формальный алгоритм превращения недетерминированного автомата без дополнительной памяти в детерминированный. Кстати, подобные алгоритмы используют реализации библиотек регулярных выражений: например, для выражения «([a-z])|([a-z]\(\))» легко составить недетерминированный автомат с неоднозначными или пустыми переходами, а алгоритм позволяет превратить его в детерминированный.
Регулярное выражение в ДКА
В промышленных библиотеках регулярных выражений многие операции избыточны и лишь для удобства. Если убрать лишнее и оставить минимум, достаточный для создания произвольных регулярных выражений, то останутся три операции:
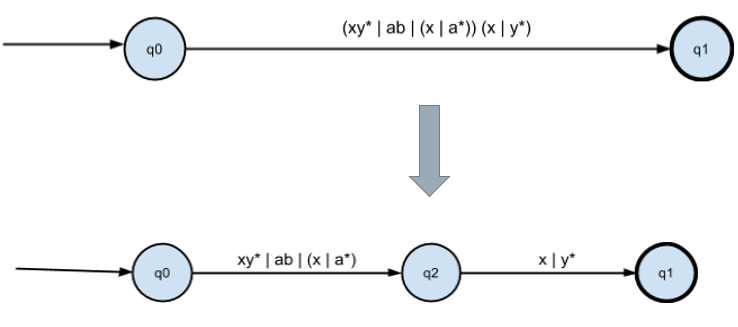
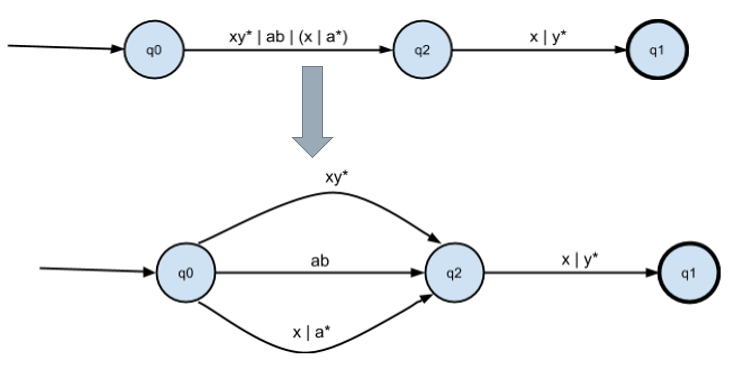
Преобразуем конкатенацию с (x | y*) :
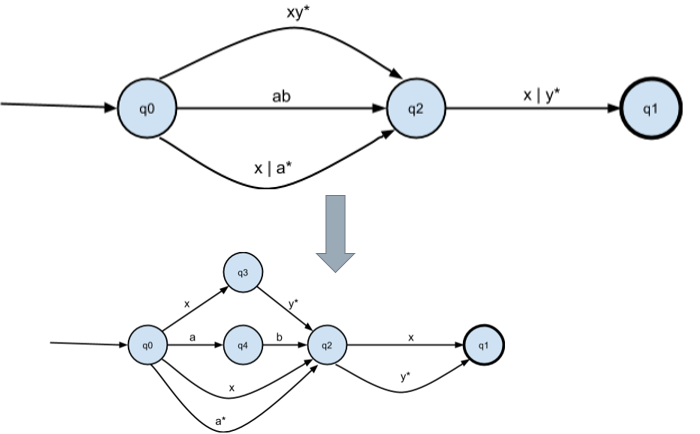
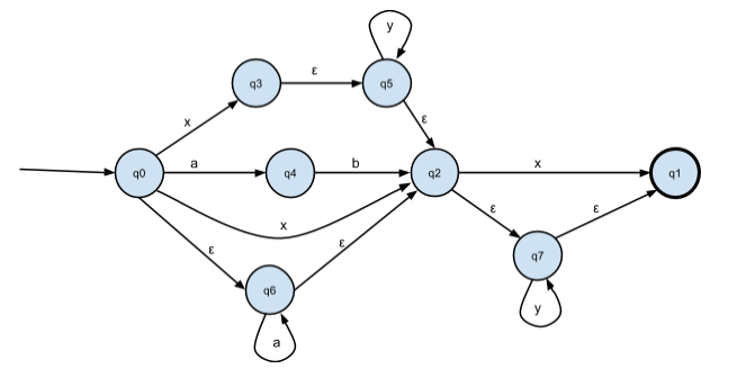
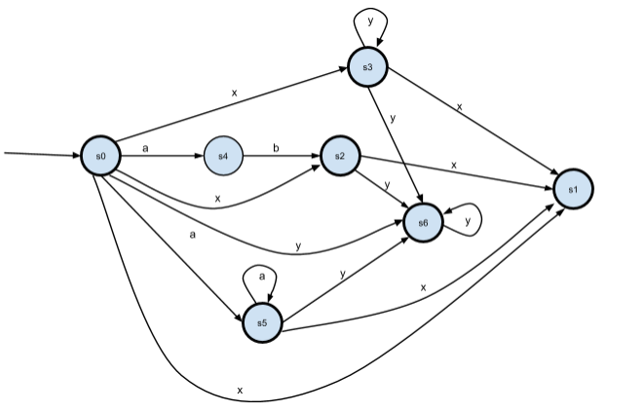
Получаем промежуточный εНКА, т.е. НКА с “пустыми” — или “самопроизвольными” — переходами:
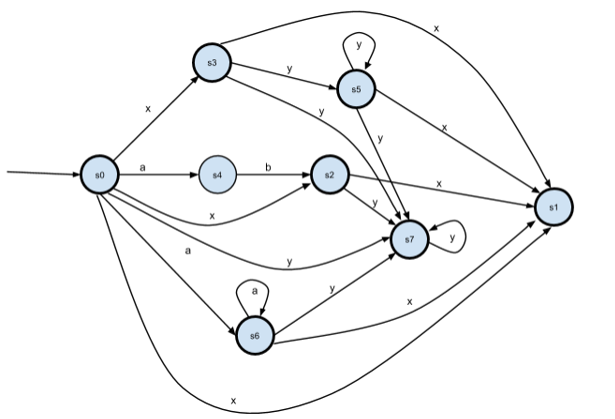
Убираем переходы по пустой цепочке ε:
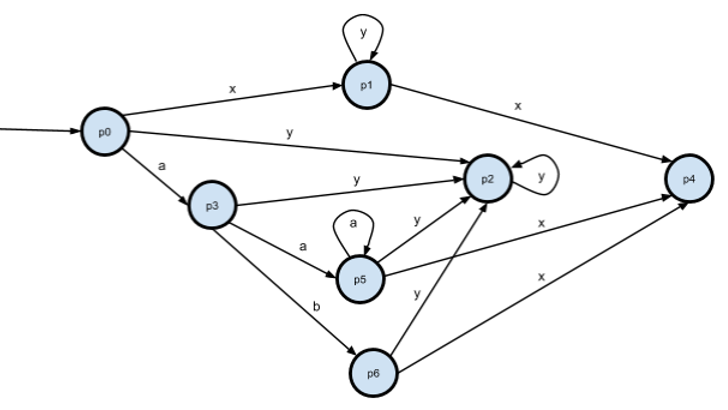
Теперь состояния s3 и s5 оказались эквивалентны. Уберём s5, переименуем s6->s5, s7->s6.
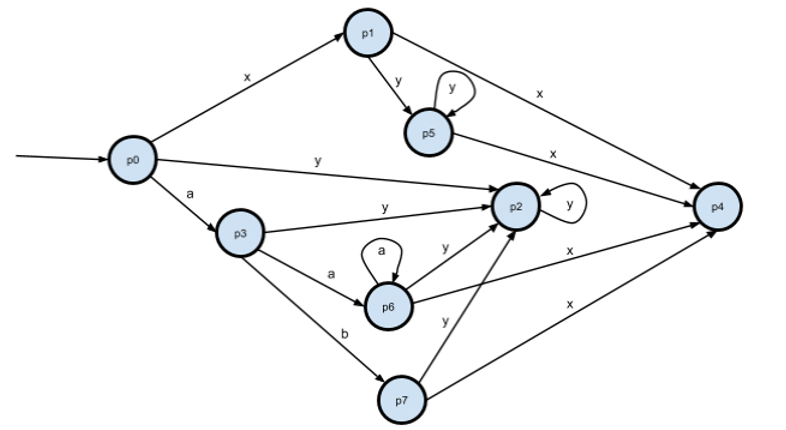
Убираем неопределённые переходы из НКА:
Теперь p1 и p5 эквивалентны. Уберём p5, переименуем p6->p5, p7->p6.
Применение конечных автоматов
Существует классификация программ по принципам их работы. Один из вариантов – это классификация Д. Харела, которая делит программы на три вида
Автоматы применяют в трансформирующих системах, особенно связанных с обработкой текста. Примером подобной системы является интерпретатор, компилятор, шаблонизатор, или же любой простой скрипт для обработки запроса к серверу:
Теория вычислений. Введение в конечные автоматы
Это до предела упрощенная модель компьютера имеющая конечное число состояний, которая жертвует всеми особенностями компьютеров такие как ОЗУ, постоянная память, устройства ввода-вывода и процессорными ядрами в обмен на простоту понимания, удобство рассуждения и легкость программной или аппаратной реализации.
С помощью КА можно реализовать такие вещи как, регулярные выражения, лексический анализатор, ИИ в играх и тд.
У конечных автоматов имеется таблица переходов, текущее состояние автомата, стартовое состояние и заключительное состояние.
Таблица переходов — В ней хранятся переходы для текущего состояния и входного символа. Простейшая реализация может быть как двумерный массив.
Здесь видно, что из состояния 0 в состояние 1 можно попасть только, если у нас будет входной символ ‘a’, из состояния 1 в состояние 2, если символ ‘b’.
Текущее состояние — множество состояний в котором автомат может находиться в данный момент времени.
Стартовое состояние — состояние откуда КА начинает свою работу.
Заключительное состояние — множество состояний в которых автомат принимает определенную цепочку символов, в ином случае отвергает.
Детерминированные конечные автоматы (deterministic finite automaton)
Простейший КА, в котором может быть одно состояние в текущий момент времени, обладает детерминированностью.
Детерминированность — для всех состояний имеется максимум и минимум одно правило для любого возможного входного символа, то есть например, для состояния 1 не может быть два перехода с одним и тем же входным символом.
Недетерминированные конечные автоматы (nondeterministic finite automaton)
НКА не является каким-то существенным улучшением ДКА, просто в нем добавлен так сказать синтаксический сахар, в виде свободных переходов, недетерминированности и множеств состояний. Реализовать можно как массив состоящий из структур в которой хранится состояние, входной символ и следующее состояние.
Свободные переходы (эпсилон переходы) — переходы, которые можно совершать без чтения входного символа.
Недетерминированность — ноль и более переходов для одного символа в каких-либо состояниях.
Множества состояний — в один момент времени НКА может находится в нескольких состояниях.
Заключительное состояние обозначается двойным кругом.
В стартовом состоянии у нас текущим состоянием является <1>, при входном символе ‘b’ у нас появляется возможность, пойти в состояние 1 и в состояние 2, то есть после входного символа ‘b’ текущим состоянием является множество <1, 2>.
Свободным переходом обозначается пунктирной линией.
Здесь видно два свободных перехода из стартового состояния, то есть без чтения входного символа мы сразу находимся в множестве состоянии <2, 4>.
Для преобразования НКА в ДКА используется алгоритм Томпсона.
При преобразовании НКА в ДКА может получиться не совсем минимальный ДКА и для его минимизации можно применить алгоритм Бржозовского.
Конечные автоматы с магазинной памятью (pushdown automaton)
Это тот же КА, но с дополнительной памятью в виде стека. Теперь для совершения перехода нужно учитывать еще несколько факторов, символ который нужно удалить из стека и символы которые нужно добавить в стек.
КАМП можно применять в таких местах, где может быть неограниченное количество вложений, например при разборе языков программирование или подсчету вложенных скобок в математических выражениях. Реализовать с помощью КА невозможно, ведь количество возможных состояний конечно в отличие от стека (я понимаю, что память тоже конечна).
Удаление символа из стека — при любом переходе решается какой символ вытолкнуть, если на вершине стека не оказалось такого символа, то он и не выталкивается. Так же если символ нужно оставить в стеке, то он добавляется вместе с добавляемыми символами.
Добавление символов в стек — при любом переходе решает какие символы добавить в стек.
Этот КАМП подсчитывает вложенность скобок, за счет добавления и удаления символов из стека.
ДАМП не равен НАМП, поэтому невозможно одно преобразовать в другое, следовательно НАМП обладает преимуществом перед ДАМП.
Машина Тьюринга (Turing machine)
Самая мощная машина из существующих, его преимущество перед другими в ленте с которой он может работать как хочет. В нем нет свободных переходов. Умеет интерпретировать другие автоматы такие как КА, КАМП.
Лента — это одномерный массив в который могут записываться данные за счет головки над ячейкой, который можно заранее заполнить входными данными.
Шаблон: считаный_символ_с_головки/записаный_символ; сторона_смещения_головки. края ленты обозначаются ‘_’.
Эта МТ выполняет инкремент двоичного числа, головка стоит слева, там где начинается лента.
ДМТ эквивалентен НМТ, так, что они тоже не различаются.
Универсальная машина Тьюринга (universal Turing machine)
Машина которая может порождать другие машины Тьюринга, получая на входную ленту данные машины.
Конечные автоматы
Введение
Конечные автоматы являются мощным инструментом для работы. Компиляторы работает на основе конечных автоматов. Любой алгоритм которые вы пишете может быть представлен в виде конечного автомата.
В конечном автомате количесто состояний конечно, а результат его работа определяется по его конченому состоянию (Wikipedia).
Существует несколько видов конечных автоматов:
Детерминированный кончечный автомат (ДКА)
Из любого состояние должен быть только один преход по символову, иначе этот автомат недерминирован.
ДКА является самым удобным из всех конченых автоматов. Его удобнее всего обработаывать, всегда стараются свести задачу к построению ДКА. Но разобрать НКА и ε-НКА также необходимо.
Недетерминированный конечный автомат(НКА)
Предположим нам надо построить автомат, который принимает все строки, состоящие из символов [0, 1], где второй символ будет 0.
ε-Недетерминированный конечный автомат (ε-НКА)
ε-НКА очень похож на НКА, только теперь мы можем преходить по ε. Теперь ничего не считав, мы сможем перейти из одной вершины в другую.
Принмает теже слова, что и предыдущий
Эквиалетность
Есть свойство у конченых автоматов — это их эквиалетность. ДКА НКА ε-НКА. Благодаря этому мы можем спокойно из ε-НКА сделать ДКА, это нам сильно пригодится.
Вкратце, разобрав какие бывают автоматы, мы можем перейти к более подробному изучению их реализации
Реализация
Обработка автомата
Как же можно проверить принимает ли данный кончечный автомат строку.
Для ДКА все очевидно. Мы храним матрицу преходов, текущее состояние (когда мы ничего не считали, тек. сотояние = начальное состояние) и терминальные вершины. Считываем по одному символу, и переходим в состояние по матрице перехода.
Для НКА вместо текущего состояния мы храним множество текущих состояний. Разберем НКА данный выше.
Пусть мы хотим перейти по символу 0. Текущее множество состояний — множество, состоящее из одной вершины — начальной. У нас есть два прехода по символу 0 => множество состояний у нас будет
Обработка ε-НКА похожа на обработку НКА. Предположим наше текущее множество S. Перед считываением следущего символа: для всех q ∈ S добавить в множество S вершину достигаемую из q по символу ε.
Детерминация автомата
Перевести автомат из ДКА в НКА легко. Нам просто ничего не нужно делать, т.к. ДКА это обобщенный случай НКА.
Но что делать если мы хотим превести из ε-НКА в ДКА (НКА является обобшенным случаем ε-НКА). Этот процесс называется детерминацией автомата.
Начнем обоходить наш ε-НКА, например, DFS-ом. Вершиной графа является множество текущих состояний. Состояниями нового ДКА будут все вершины графа. При переходе к новой веришне мы выбираем символ по которому хотим перейти, и добавляем этот переход. Приведу псевдокод DFS-a для большой ясности:
Если в множестве есть терминальное состояние, то состояние нового ДКА будет тоже терминальным.
К сожалению число состояние нового ДКА будет расти экспоненциально, что не очень хорошо, т.к. это будет потреблять много памяти.
Алгоритм минимизации ДКА
Любой ДКА имеет эквиалетный ему ДКА с минимальным числом состояний. Как его «сжать»? Заметим, что неразличимые вершины мы можем соединить в одну.
Что такое различимое состояние?
Состояние p и q являются различимыми, если есть такое слово s, что преходя из вершины p по слову s мы попадаем в терминальное состояние, а из вершины q в не-терминальное, или наоборот.
1) Терминальное и не-терминальное состояние являются различимыми. Перейдем по пустому слову и окажемся в двух различимых состояниях.
2) Состояния a и b различимы. Если существуют состояния c и d, и из c есть переход по символу x в состояние a, а из веришны d есть переход по символу x в состояние b, то состояние a и b различимы.
Мы нашли все различимые состояния. Теперь нам надо «схлопнуть» все неразличимые.
Регулярные выражения
Регулярные варжения напрямую связаны с конечными автоматами. Введем некоторые обозначения:
∅ — пустое множество.
ε — строка, которая не сожержит символов.
Пусть A и B регулярные выражения. L(A) и L(B) — кончечные языки, которые данные регулярные варжения задают.
Это основные операции прменимые к регулярным варжением. Можно всетрить и другие, но все они могут быть представлены операциями данными выше.
Вот представление основных операций регулярных выражений в виде ε-НКА.
Дале разбираем это выражение рекурсивным спуском и строим ε-НКА.
Чтобы обработать Регулярное выражение построим для ε-НКА, а потом получим из ε-НКА ДКА, который очень легко обрабатывать.
Конечный автомат
Из Википедии — свободной энциклопедии
Коне́чный автома́т (КА) — (в теории алгоритмов) — математическая абстракция, модель дискретного устройства, имеющего один вход, один выход и в каждый момент времени находящегося в одном состоянии из множества возможных. Является частным случаем абстрактного дискретного автомата, число возможных внутренних состояний которого конечно.
При работе на вход КА поступают последовательно входные воздействия, а на выходе КА формирует выходные сигналы. Обычно под входными воздействиями принимают подачу на вход автомата символов одного алфавита, а на выход КА в процессе работы выдаёт символы в общем случае другого, возможно даже не пересекающегося со входным, алфавита.
Помимо конечных автоматов существуют и бесконечные дискретные автоматы — автоматы с бесконечным числом внутренних состояний, например, машина Тьюринга.
Переход из одного внутреннего состояния КА в другое может происходить не только от внешнего воздействия, но и самопроизвольно.
Различают детерминированные КА — автоматы, в которых следующее состояние однозначно определяется текущим состоянием и выход зависит только от текущего состояния и текущего входа, и недетерминированные КА, следующее состояние у которых в общем случае неопределённо и, соответственно, не определён выходной сигнал. Если переход в последующие состояния происходит с некоторыми вероятностями, то такой КА называют вероятностным КА.
Примерами физической реализации КА могут служить любые цифровые системы, например, компьютеры или некоторые логические узлы компьютеров с памятью — триггеры и другие устройства. Комбинационная последовательная логика не может являться КА, так как не имеет внутренних состояний (не имеет памяти).
С абстрактной точки зрения КА изучает раздел дискретной математики — теория конечных автоматов.
Основы теории вычислительных систем: машина с конечным числом состояний
Теория вычислительных систем — это то, что позволяет нам программировать. Однако, можно писать программы и без представления о концепциях, скрывающихся за вычислительными процессами. Не то, чтобы это было плохо — когда мы программируем, то работаем на намного более высоком уровне абстракции. В конце концов, когда мы ведём машину, то концентрируемся только на двух или трёх педалях, переключателе передач и руле. Для повседневной неспешной езды этого более чем достаточно. Однако, если мы хотим управлять автомобилем на пределе его возможностей, то тут нужно знать гораздо больше, чем просто три педали, КПП и руль.
Такой подход справедлив и в программировании. Большая часть повседневной мирской работы может быть выполнена при минимальном знании теории вычислительных систем или даже вообще без него. Не нужно понимать теорию категорий, чтобы накидать форму «Контакты» в PHP. Тем не менее, если вы планируете писать код, требующий серьёзных вычислений, то тут уж придётся разобраться с тем, что у этих самых вычислений под капотом.
Цель этой статьи — представить некоторые фундаментальные основы вычислений. Если это окажется интересным, то в дальнейшем я могу написать более продвинутый топик на эту тему, но прямо сейчас я хочу просто рассмотреть логику простейшего абстрактного вычислительного устройства — машины с конечным числом состояний (finite state machine).
Машина с конечным числом состояний
Машина с конечным числом состояний (finite state machine, FSM), или конечный автомат (finite automaton) — это математическая абстракция, используемая при проектировании алгоритмов. Говоря простым языком, машина с конечным числом состояний умеет считывать последовательности входных данных. Когда она считывает входной сигнал, то переключается в новое состояние. Куда именно переключится, получив данный сигнал, — заложено в её текущем состоянии. Звучит запутанно, но на самом деле всё очень просто.
Представим устройство, которое читает длинную бумажную ленту. На каждом дюйме этой ленты напечатана буква — a или b.
Как только устройство считывает букву, оно меняет своё состояние. Вот очень простой граф переходов для такой машины:
Кружки — это состояния, в которых машина может быть. Стрелочки — переходы между ними. Так что, если вы находитесь в состоянии s и считываете a, то вам необходимо перейти в состояние q. А если b, то просто остаётесь на месте.
Итак, если изначально мы находимся в состоянии s и начинаем читать ленту из первого рисунка слева направо, то сначала будет прочитана a, и мы переместимся в состояние q, затем b — вернёмся обратно в s. Следующая b оставит нас на месте, а a вновь переместит в q. Элементарно, но какой в этом смысл?
Оказывается, если пропустить ленту с буквами через FSM, то по её итоговому состоянию можно сделать некоторые выводы о последовательности букв. Для приведённго выше простого конечного автомата финальное состояние s означает, что лента закончилась буквой b. Если же мы закончили в состоянии q, то последней на ленте была буква a.
Это может показаться бессмысленным, но существует масса задач, которые можно решить с помощью такого подхода. Простейший пример: определить, содержит ли HTML-страница следующие теги в заданном порядке:
Также конечный автомат может использоваться для представления механизмов парковочного счётчика, автомата с газировкой, автоматизированного газового насоса и тому подобных штук.
Детерминированная машина с конечным числом состояний (Deterministic Finite State Machine)
Машины с конечным числом состояний, которые мы рассматривали выше, являются детерминированными. У них из любого состояния существует только один переход для любого разрешённого входного сигнала. Другими словами, не существует двух различных путей из данного состояния, когда вы считываете, допустим, букву a. На первый взгляд такое ограничение кажется глупым.
Недетерминированная машина с конечным числом состояний (Nondeterministic Finite State Machine)
Итак, надо распознать букву a с последующим нулём или более одинаковых букв b или c и с замыкающей следующей буквой алфавита. Самый простой способ отобразить этот алгоритм с помощью машины с конечным числом состояний представлен ниже. Финальное состояние t означает, что строка была принята целиком и соответствует шаблону.
На этом принципе основан алгоритм большинства шахматных программ. Они просматривают все возможности всех возможных ходов на данном этапе и выбирают ту стратегию, которая в данный момент даёт максимальное преимущество над противником.
Регулярные выражения
Если вы когда-нибудь занимались любым видом программирования, то вы почти наверняка сталкивались с регулярными выражениями (regular expressions). Регулярные выражения и машины с конечным числом состояний функционально эквивалентны. Всё, что можно допустить для (или связать с) регулярным выражением, можно допустить для (или связать с) конечным автоматом. Например, шаблон, который мы разбирали выше, можно связать с
Это положение известно как лемма о накачке для регулярных языков. Её основная мысль: если ваш шаблон имеет блок, который может быть повторён более, чем один раз, то этот шаблон не является регулярным. Другими словами, ни регулярные выражения, ни машины с конечным числом состояний не могут быть сконструированы так, чтобы распознавать все строки, которые можно связать с шаблоном.
Машина Тьюринга
Так как же нам распознавать нерегулярные шаблоны? Существует теоретическое устройство, подобное конечному автомату и называемое машиной Тьюринга (Turing Machine). Как и у машины с конечным числом состояний, у него имеется бумажная лента, с которой оно считывает информацию. Однако, машина Тьюринга также способна записывать и стирать данные на ленте. Полное объяснение принципов этого устройства займёт больше места, чем у нас здесь имеется, поэтому я обозначу лишь несколько важных моментов, относящихся к нашей дискуссии о машинах с конечным числом состояний и регулярных выражениях.
Машина Тьюринга вычислительно полна, и всё, что в принципе может быть вычислено, может быть вычислено с помощью машины Тьюринга. А благодаря способности записывать данные на ленту с такой же лёгкостью, как и считывать их с ленты, она не ограничена конечным числом состояний. Бумажную ленту можно представить, как имеющую бесконечную длину. Очевидно, что современные компьютеры не обладают бесконечным количеством памяти, однако, они имеют её достаточно, чтобы вы не вышли за предел для тех типов задач, которые они способны обработать.
Машина Тьюринга предоставляет нам воображаемое механическое устройство, позволяющее визуализировать и понять, как работает вычислительный процесс. Это особенно полезно для понимания пределов вычислений. Если это интересно, то в будущем я могу написать отдельную статью о машине Тьюринга.
Почему это имеет значение?
Понимание, что машины с конечным числом состояний и регулярные выражения функционально эквивалентны, открывает невероятно интересные способы применения движков регэкспов. Особенно, когда дело доходит до создания бизнес-правил, которые могут быть изменены без перекомпиляции всей системы.
Знание основ теории вычислительных систем позволяет вам брать проблему X, которую вы понятия не имеете как решать, и применять к ней подход: «Я не знаю, как решить X, но я знаю, как решить Y и как привести решение для Y к решению для X. Вот почему теперь я знаю, как решить X».