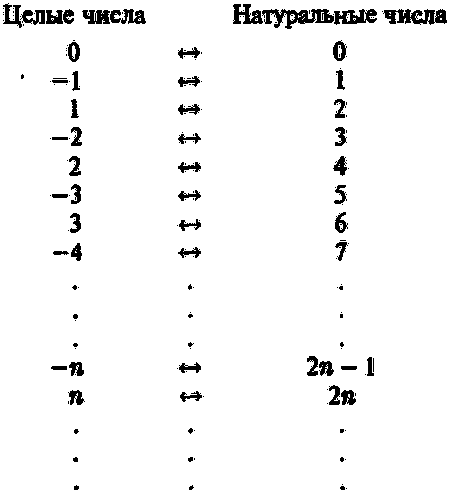Действительных чисел больше чем натуральных

Числа: натуральные, целые, рациональные, иррациональные, действительные

Натуральные числа

Натуральные числа определение – это целые положительные числа. Натуральные числа используют для счета предметов и многих иных целей. Вот эти числа:

Это натуральный ряд чисел.
Ноль натуральное число? Нет, ноль не является натуральным числом.
Сколько натуральных чисел существует? Существует бесконечное множество натуральных чисел.
Каково наименьшее натуральное число? Единица — это наименьшее натуральное число.
Каково наибольшее натуральное число? Его невозможно указать, ведь существует бесконечное множество натуральных чисел.

Сумма натуральных чисел есть натуральное число. Итак, сложение натуральных чисел a и b:

с — это всегда натуральное число.

Произведение натуральных чисел есть натуральное число. Итак, произведение натуральных чисел a и b:

с — это всегда натуральное число.

Разность натуральных чисел Не всегда есть натуральное число. Если уменьшаемое больше вычитаемого, то разность натуральных чисел есть натуральное число, иначе — нет.

Частное натуральных чисел Не всегда есть натуральное число. Если для натуральных чисел a и b

где с — натуральное число, то это значит, что a делится на b нацело. В этом примере a — делимое, b — делитель, c — частное.

Делитель натурального числа — это натуральное число, на которое первое число делится нацело.

Каждое натуральное число делится на единицу и на себя.

Простые натуральные числа делятся только на единицу и на себя. Здесь имеется ввиду делятся нацело. Пример, числа 2; 3; 5; 7 делятся только на единицу и на себя. Это простые натуральные числа.

Единицу не считают простым числом.

Числа, которые больше единицы и которые не являются простыми, называют составными. Примеры составных чисел:

Единицу не считают составным числом.

Множество натуральных чисел составляют единица, простые числа и составные числа.

Множество натуральных чисел обозначается латинской буквой N.

Свойства сложения и умножения натуральных чисел:

переместительное свойство сложения

сочетательное свойство сложения

переместительное свойство умножения

сочетательное свойство умножения

распределительное свойство умножения

Целые числа

Целые числа — это натуральные числа, ноль и числа, противоположные натуральным.

Числа, противоположные натуральным — это целые отрицательные числа, например:

Множество целых чисел обозначается латинской буквой Z.

Рациональные числа

Рациональные числа — это целые числа и дроби.

Любое рациональное число может быть представлено в виде периодической дроби. Примеры:

Из примеров видно, что любое целое число есть периодическая дробь с периодом ноль.

Любое рациональное число может быть представлено в виде дроби m/n, где m целое число,n натуральное число. Представим в виде такой дроби число 3,(6) из предыдущего примера:

Другой пример: рациональное число 9 может быть представлено в виде простой дроби как 18/2 или как 36/4.

Множество рациональных чисел обозначается латинской буквой Q.

Подробнее о рациональных числах в разделе Рациональные числа.

Иррациональные числа

Иррациональные числа — это бесконечные непериодические десятичные дроби. Примеры:

Подробнее об иррациональных числах в разделе Иррациональные числа.

Действительные числа

Действительные числа – это все рациональные и все иррациональные числа.

Множество действительных чисел обозначается латинской буквой R.

Источник

Действительные числа

Определение действительных чисел

Рациональные числа объединяют в себе целые числа и дробные числа. А действительные числа объединяют рациональные и иррациональные числа. Отсюда сформулируем определение действительных чисел:

Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Множество рациональных чисел —

Иррациональное число — это число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби m/n. Оно может быть выражено в форме бесконечной непериодической десятичной дроби. Множество иррациональных чисел —

Множество действительных чисел состоит из множества рациональных чисел вместе с множеством иррациональных чисел. Это множество R иначе обозначается как область действительных чисел (-∞; +∞). Можно записать так, что R есть объединение двух множеств: рациональных и иррациональных чисел:

Так как любое рациональное число может быть записано в виде конечной десятичной дроби или бесконечной периодической дроби, а иррациональные числа представляются бесконечными непериодическими десятичными дробями, то определение действительных чисел можно сформулировать по-другому.

Действительные числа — это числа, которые можно записать в виде конечной или бесконечной, периодической или непериодической десятичной дроби. Их иногда называют вещественными.

Примеры действительных чисел:

Число нуль также является действительным числом, так как 0 — рациональное число.

Из определения действительных чисел можно сделать вывод, что существуют как положительные, так и отрицательные действительные числа, а нуль — ни положительное, ни отрицательное действительное число.

При помощи действительных чисел можно описать величины, значения которых могут изменяться непрерывно. Проще говоря, действительные числа дают возможность численно выражать значение непрерывно изменяющейся величины через единичное значение этой величины.

Действительные числа на координатной прямой

Координатная прямая — это прямая, которая изображается с определенной точкой отсчета, которая принимается за 0, единичным отрезком и заданным направлением движения.

Интересный факт: действительные числа заполняют каждую точку координатной прямой.

Каждой точке координатной прямой соответствует единственное действительное число — координата этой точки. При этом каждому действительному числу соответствует единственная точка на координатной прямой. То есть, между действительными числами и точками координатной прямой существует взаимно однозначное соответствие.

Представления действительных чисел

По определению действительными числами являются:

Часто можно встретить действительные числа в виде корней, степеней, логарифмов и др. Кроме того, сумма, разность, произведение и частное действительных чисел также представляют собой действительные числа.

Также из действительных чисел с помощью арифметических знаков, знаков корня, степеней, логарифмических, тригонометрических функций можно составлять числовые выражения, значения которых также будут действительными числами. Например, значения выражений

будут действительные числа.

Сравнение действительных чисел

Любые действительные числа можно сравнивать. Для сравнения действительных чисел есть два способа:

Источник

Действительных чисел больше чем натуральных

Масса и энергия

Счётно ли бесконечное множество вещественных чисел?

Можно ли объединить в пары бесконечное множество вещественных чисел и бесконечное множество натуральных чисел? Считается, что это невозможно. Даже в промежутке между 0 и 1 вещественных чисел больше, чем натуральных чисел в бесконечном множестве натуральных чисел. Так как невозможно составить взаимно – однозначное соответствие между вещественными числами этого промежутка и натуральными числами. Чтобы каждому вещественному числу сопоставлялось одно и только одно число натуральное. Попробуем осуществить такое сопоставление.

Натуральные числа можно располагать по порядку: 1, 2, 3, 4, 5 и т.д. Вещественные числа так выстроить нельзя. Во множество вещественных чисел входят как рациональные, так и иррациональные числа. Иррациональные числа имеют бесконечное количество знаков после запятой. Поэтому бесконечное множество вещественных чисел, обычно объединяют в матрицу, у которой числа вниз и цифры вправо уходят в бесконечность. Каждой строке соответствует одно вещественное число. Например:

Нам необходимо сформировать правило взаимно – однозначного сопоставления вещественных чисел промежутка 0 – 1, и натуральных чисел. Таких правил сопоставления можно составить бесконечно много. Но мы возьмём одно простое правило, чтобы у нас получилась симметрия сопоставляемых множеств.

Итак, правило сопоставления вещественных чисел промежутка 0 – 1 и натуральных чисел: В каждой паре чисел, первому знаку после запятой у вещественного числа соответствует цифра единиц числа натурального, второму – цифра десятков, третьему цифра сотен, четвёртому цифра тысяч и т.д.

Цифры у вещественных и натуральных чисел будут соответствовать:

1 → 1, 2 → 2, 3 → 3, 4 → 4, 5 → 5, 6 → 6, 7 → 7, 8 → 8, 9 → 9, 0 → 0.

Согласно этому простому правилу, у нас получается зеркальное расположение цифр в паре вещественное число – число натуральное.

Для полной симметрии матрицу можно представить так:

В актуальной бесконечности, каждому вещественному числу промежутка 0 – 1 будет соответствовать одно и только одно натуральное число. Значит мощность бесконечного множества вещественных чисел промежутка 0 – 1 и бесконечного множества натуральных чисел одинакова.

Какие могут возникнуть возражения?

1. А почему натуральные числа расположены не по порядку?

Обычно натуральные числа располагают в ряд 1, 2, 3, 4, 5 и т.д., потому что есть такая возможность. Но если мы поменяем порядок расположения? От этого, что измениться количество натуральных чисел? Если бы это было так, то уже давно изучали отличительные свойства рядов натуральных чисел, расположенных в различном порядке.

Матрица у нас симметричная, и поэтому можно задать встречный вопрос: почему во всех доказательствах превосходящей мощности вещественных чисел, в матрице вещественные числа расположены не по порядку? Как только вещественные числа будут расположены по возрастанию или убыванию, не составит труда объединить их в пары с натуральными числами.

2. Применяя диагональный процесс, методом от противного, можно доказать несчётность вещественных чисел.

Правило применённое в этом диагональном процессе: если по диагонали цифра 1, то в числе, не входящем в перечень пишем 9, во всех других случаях пишем 1.

Матрица сопоставления вещественных чисел промежутка 0 – 1 и натуральных чисел у нас симметричная, поэтому диагональный процесс можно провести, по этому же правилу, и в части натуральных чисел. И получить натуральное число соответствующее вещественному числу, не вошедшему в рассматриваемый фрагмент бесконечной матрицы.

О чём говорит нахождение числа, не входящего в рассматриваемый фрагмент матрицы? Только о том, что его нет в рассматриваемом фрагменте. Но во всей бесконечной матрице оно есть, и есть соответствующая пара вещественное число – число натуральное. (Почему всё-таки можно найти число не входящее в рассматриваемый фрагмент бесконечной матрицы рассмотрено в статье «Корректен ли диагональный метод?». Ответу на этот вопрос посвещено не мало мест в альманахе MOI в материалах Валдиса Валевича Эгле и Марины Олеговны Ипатьевой).

3. Натуральные числа всегда конечные, а в матрице это не видно. Бывают ли такие большие натуральные числа, состоящие из бесконечной последовательности цифр, уходящей влево?

Можно ответить встречным предложением – назовите самое большое натуральное число, больше которого нет натуральных чисел.

Почему для иррациональных чисел, бесконечная последовательность цифр после запятой вправо считается нормальным явлением, а для натуральных чисел, бесконечная последовательность цифр до запятой влево вызывает вопросы? Ведь множество натуральных чисел бесконечно.

Попробуем получить взаимно – однозначное соответствие между вещественными числами и числами натуральными. Запятая, у вещественных чисел может располагаться в любом месте. Возьмём такой пример фрагмента матрицы вещественных чисел:

Правило для сопоставления вещественных чисел промежутка 0 – 1 и натуральных чисел, которое мы применяли выше, не подходит. Так как запятая, отделяющая целую часть вещественного числа, может находиться где угодно. И поэтому, необходимо создать новое правило (таких правил сопоставления можно создать бесконечное количество).

Правило взаимно – однозначного сопоставления вещественных чисел и натуральных чисел:

В каждой паре чисел первой цифре вещественного числа соответствует цифра единиц числа натурального, второй цифре – цифра сотен, третей – цифра десятков тысяч и т.д.

Чётные цифры (справа на лево) у натуральных чисел зарезервируем для запятой у чисел вещественных. Если есть запятая, то ставим единицу, если нет, то 0.

Цифры у вещественных и натуральных чисел будут соответствовать:

1 → 1, 2 → 2, 3 → 3, 4 → 4, 5 → 5, 6 → 6, 7 → 7, 8 → 8, 9 → 9, 0 → 0.

По нашему правилу, при каждом шаге рассматриваемого фрагмента матрицы – часть матрицы с натуральными числами будет расширяться влево вдвое быстрее, чем правая часть с вещественными числами. Так как на каждую цифру вещественного числа приходится две цифры числа натурального. Правая цифра сопоставляется цифре вещественного числа, левая описывает, есть ли после этой цифры у вещественного числа запятая.

Такое сопоставление ничуть не хуже взаимно – однозначного сопоставления чётных и натуральных чисел. При переходе к актуальной бесконечности, матрица у нас бесконечна вправо, влево и вниз.

Пример фрагмента нашей матрицы:

Каждому вещественному числу соответствует одно и только одно число натуральное. В каждом вещественном числе есть только одна запятая, отделяющая целую часть числа. По нашему правилу мы зарезервировали бесконечное число цифр, для отображения запятой. Бесконечное количество натуральных чисел не участвует в нашем взаимно-однозначном соответствии. Однако на каждое вещественное число есть число натуральное. Значит ли это – что мощность бесконечного множества натуральных чисел больше мощности бесконечного множества всех вещественных чисел? Составляя взаимно – однозначное соответствие натуральных и вещественных чисел промежутка 0 – 1, мы получили, что их одинаковое количество, и «лишних» натуральных чисел нет. Нет ли тут противоречия?

Противоречия нет, если мы примем, что «мощность» сравниваемых бесконечных множеств, не имеет отношения к самим бесконечным множествам, а относится к правилам сопоставления. Какие мы примем правила – такой результат и получим.

И поэтому я считаю, что сравнение мощностей бесконечных множеств есть занятие пустое и бесперспективное, так как к самим бесконечным множествам это сравнение не имеет никакого отношения.

Рассмотрим совсем простой пример. Сравним мощность бесконечного множества натуральных чисел и бесконечного множества чётных чисел. Мы можем принять различные правила сопоставления наших множеств. Например, сопоставим по порядку натуральные и чётные числа:

Каждому натуральному числу соответствует одно и только одно чётное число. Так как множества у нас бесконечные, то при переходе к актуальной бесконечности каждому натуральному числу соответствует чётное число. Значит мощность множеств у нас одинаковая.

Теперь изменим правила. Каждому числу бесконечного множества чётных чисел сопоставим чётные числа из множества натуральных чисел:

Каждому числу бесконечного множества чётных чисел соответствует одно и только одно число из бесконечного множества чисел натуральных. А у бесконечного множества натуральных чисел половина чисел осталось без пары. Значит ли это – что натуральных чисел вдвое больше?

Изменяя правила сопоставления, мы можем получить какой угодно результат. Что натуральных чисел у нас втрое, в вчетверо и т.д. больше чем чётных чисел. А можем получить, что чётных чисел больше, чем натуральных в любое количество раз. Всё зависит от правил взаимно – однозначного сопоставления. К самим бесконечным множествам это не имеет ни какого отношения. Понятие «счётность» бесконечного множества, как и понятие «мощность» бесконечного множества к бесконечным множествам неприменимо.

Источник

Сколько же всего действительных чисел?

Сколько же всего действительных чисел?

Давайте остановимся на минутку, чтобы оценить всю колоссальность обобщения при переходе от рациональных чисел к действительным.

Вначале может показаться, что целых чисел больше, чем натуральных, поскольку каждое натуральное число является целым, в то время как некоторые целые числа (а именно отрицательные) натуральными не являются. Аналогично может создаться впечатление, что дробей больше, чем целых чисел. Однако это не так. Согласно мощной и очень красивой теории бесконечных чисел, разработанной в конце XIX века Георгом Кантором — исключительно самобытным немецким математиком русского происхождения, — общее число дробных чисел, общее количество всех целых чисел и число всех натуральных чисел равны одному и тому же бесконечному числу, обозначаемому N 0 [60] «алеф-нуль»). (Удивительно, что похожая идея была частично предвосхищена еще за 250 лет до этого в начале XVII века великим итальянским физиком и астрономом Галилео Галилеем. Мы вспомним о некоторых других достижениях Галилея в главе 5.) Равенство количества целых чисел количеству натуральных чисел видно из следующего взаимно-однозначного соответствия:

Обратите внимание, что каждое целое число (в левом столбце) и каждое натуральное число (в правом столбце) встречаются один и только один раз в своем списке. В канторовской теории множеств именно существование такого рода взаимно-однозначного соответствия устанавливает факт равенства числа объектов в левом столбце числу объектов в правом столбце. Таким образом, число целых чисел действительно равно числу натуральных чисел. В данном случае это число бесконечно, но это не Имеет значения. (Единственное необычное свойство бесконечных чисел состоит в том, что даже если мы исключим некоторые элементы одного из списков, мы можем установить взаимно-одиозначное соответствие между элементами двух списков.) Аналогичным, хотя и несколько более сложным образом, устанавливается взаимно-однозначное соответствие между дробными и целыми числами. (Для этого можно использовать какой-либо из способов представления пар натуральных чисел — числителей и знаменателей — через отдельные натуральные числа; см. главу 2, «Двоичная запись цифровых данных») Множества, которые можно поставить во взаимно-однозначное соответствие с рядом натуральных чисел, называются счетными; таким образом, счетные бесконечные множества — это множества, состоящие из N 0 элементов. И, как мы только что убедились, множество целых чисел, равно как и множество дробных чисел, является счетным.

Существуют ли множества, не являющиеся счетными? Несмотря на расширение натуральной системы чисел сначала целыми, а затем и рациональными числами, общее число рассматриваемых объектов не увеличилось. Как мы убедились, число объектов во всех случаях осталось счетным. У читателя теперь может создаться впечатление, что все бесконечные множества счетны. Это не так, поскольку ситуация меняется коренным образом при переходе к действительным числам. Одним из замечательных достижений Кантора явилось доказательство того, что действительных чисел больше, чем натуральных. При этом Кантор применил так называемый диагональный процесс, который упоминался в главе 2 и который Тьюринг использовал в своем доказательстве неразрешимости проблемы остановки Для машин Тьюринга. Доказательство Кантора, как и более позднее доказательство Тьюринга, — это доказательство от противного. Предположим, что утверждение, справедливость которого мы хотим установить, на самом деле ложно, то есть множество действительных чисел счетно. Тогда множество действительных чисел в интервале от 0 до 1 должно быть заведомо счетным и должен существовать какой-нибудь список, устанавливающий взаимно-однозначное соответствие между рассматриваемым множеством действительных чисел и множеством натуральных чисел, наподобие вот этого:

Жирным шрифтом выделены диагональные десятичные знаки. В данном случае эти цифры равны:

1, 4, 1, 0, 0, 3, 1, 4, 8, 5, 1…..

Метод диагонального процесса состоит в построении действительного числа (в интервале от 0 до 1), чье десятичное разложение (после десятичной запятой) отличается в каждом разряде от соответствующего числа приведенной выше последовательности. Для определенности положим, что цифра данного разряда равна 1, если цифра соответствующего разряда на диагонали отлична от 1, и равна 2, если цифра на диагонали равна 1. Таким образом, в рассматриваемом случае получается такое действительное число:

Это действительное число не может быть в списке, поскольку оно отличается от первого числа в первом десятичном разряде (после десятичной запятой), от второго числа — во втором разряде, от третьего числа — в третьем разряде и т. д. Таким образом, мы приходим к противоречию, поскольку полагали, что рассматриваемый список содержит все действительные числа в интервале от 0 до 1. Из этого противоречия следует истинность утверждения, которое нам требовалось доказать, — а именно, что не существует взаимно-однозначного соответствия между множеством действительных чисел и множеством натуральных чисел и, соответственно, что число действительных чисел больше числа рациональных чисел и не является счетным.

Число действительных чисел равно бесконечному числу, обозначаемому С. (Здесь С является сокращенным обозначением слова континуум — другого названия системы действительных чисел.) Может возникнуть вопрос, почему мы не обозначаем это число, например, N 1. Символ N 1 на самом деле обозначает следующее за N 0 бесконечное число, а вопрос о том, верно ли утверждение С = N 1 — это так называемая континуум-гипотеза, — представляет собой знаменитую и пока что нерешенную проблему.

При этом следует отметить, что множество вычислимых чисел счетно. Пересчитать их можно просто перечислив по порядку машины Тьюринга, порождающие действительные числа (то есть машины, последовательно порождающие цифры каждого разряда действительных чисел). При этом можно исключить из списка любую машину Тьюринга, порождающую действительное число, которое уже встречалось ранее в списке. Поскольку множество машин Тьюринга счетно, то, следовательно, счетным также должно быть и множество вычислимых действительных чисел. Почему же нельзя применить диагональный процесс к этому списку с тем, чтобы породить новое не включенное в список вычислимое число? Ответ состоит в том, что в общем случае невозможно с помощью вычислений решить, следует ли ту или иную машину Тьюринга включать в список, поскольку для этого мы должны были бы иметь возможность решить проблему остановки. Некоторые машины Тьюринга, начав порождение цифр действительного числа, могут зависнуть и оказаться уже не в состоянии выдать очередную цифру (поскольку они «не остановятся»). Не существует вычислимого способа, который позволил бы решить, какие именно машины Тьюринга зависнут таким образом. Это, в сущности, и есть проблема остановки. Значит, хотя метод диагонального процесса и породит некоторое действительное число, последнее не будет вычислимым. На самом деле, это рассуждение может использоваться для доказательства существования невычислимых чисел. Именно в этом ключе выдержано описанное в предыдущей главе тьюринговское доказательство существования классов алгоритмически неразрешимых задач. Другие области применения диагонального процесса будут рассмотрены дальше.

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

Читайте также

Головоломные ряды чисел

Головоломные ряды чисел Похоже, что остальных участников ежегодного конкурса головоломок не очень-то обрадовало это сообщение. В головоломке, изображенной на рисунке, требовалось определить четыре следующие цифры в ряду представленных чисел. Держите носовой платок

Могущество чисел

Могущество чисел За последние годы вышло несколько очень хороших книг, в них утверждается, что Америка движется в двух основных направлениях. Эта книга доказывает обратное. Америка движется в сотнях разных направлений. Одновременно. Быстро. Это часть нашей великой

Глава XX. (Что) Он прежде всего и после всего, даже вечного

Глава XX. (Что) Он прежде всего и после всего, даже вечного Итак, Ты наполняешь все и охватываешь, Ты прежде и после всего. И впрямь, Ты прежде всего, потому что Ты существуешь до того, как все это возникло. Но как Ты — после всего? То есть как Ты после тех вещей, которые не имеют

Свойства действительных намерений

Свойства действительных намерений Вот что нужно знать и помнить о свойствах и качествах Действительных намерений.Свойство №1: Действительные намерения у людей могут проявляться В ЛЮБЫЕ моменты времени. Они могут «включиться» чем угодно (и человек этого даже не заметит):

О действительных целях общения

О действительных целях общения Зачем общаются люди, с какими целями? Хочется надеяться, что вы, читатель, уже вдоволь наслушались деклараций и теперь хотите узнать Действительное положение дел с целями общения.Истина: Действительными целями ЛЮБОГО общения ЛЮБОГО

Об источнике и причине существования действительных намерений

Об источнике и причине существования действительных намерений Эта глава является достаточно сложной для восприятия. Справиться с этим можно: прочитайте ее не спеша столько раз, сколько вам нужно. Вы вполне сможете понять то, что в ней написано.Итак, начнем.Поскольку

Об источнике и причине существования действительных намерений

Об источнике и причине существования действительных намерений Эта глава является достаточно сложной для восприятия. Справиться с этим можно: прочитайте ее не спеша столько раз, сколько Вам нужно. Вы вполне сможете понять то, что в ней написано. Итак, начнем.Поскольку

О действительных целях общения

О действительных целях общения Зачем общаются люди, с какими целями? Хочется надеяться, что Вы, Читатель, уже вдоволь наслушались Деклараций и теперь хотите узнать действительное положение дел с целями общения.ИСТИНА: Любой человек, который либо сам начинает с Вами

Лекция III Символизм Чисел

Лекция III Символизм Чисел Оккультные знаки и символы.Штутгарт, 15 Сентября 1907GA 101Сегодня мы займемся рассмотрением того, что называется символизмом чисел. Если говорить об оккультных знаках и символах необходимо упомянуть символы, которые выражены в числах, даже если

Символица чисел в сказках

Символица чисел в сказках Ноль Ноль предшествует единице, это то небытие, первозданный океан хаоса, о котором повествуют мифы разных народов, из которого рождается Логос – единица и куда все, пройдя свой путь развития,

Значимость чисел

«Действительность» действительных чисел

«Действительность» действительных чисел Если отвлечься от понятия вычислимости, то действительные числа называются «действительными», потому что они, как представляется, дают величины, необходимые для измерения расстояний, углов, времени, энергии, температуры и многих

Магия чисел

Магия чисел Сегодня, хотя большинство людей мало знают о свойствах чисел, относящихся к необщепринятой реальности, многие до сих пор верят, как и столетия назад, что числа обладают магическими свойствами. Точно так же, как мы используем особые геометрии, чтобы строить

Математика мнимых чисел

Математика мнимых чисел История развития мнимых чисел весьма интересна, так как она следует по пути постоянных (и не вполне успешных) попыток избавиться от «вторичных качеств» природы. В XVII в. математики Джон Уоллис (1616-1703) и Готфрид Лейбниц (1646-1716), наряду с другими,

Иерархия чисел

Иерархия чисел Рассмотрим еще некоторые особенности комплексных чисел. Отметьте, например, что, хотя между комплексными и действительными числами существует сходство, между ними есть и различия. Помните – можно сказать, что 5 больше, чем 3, но нельзя сказать, что

Источник