Диагональ параллелограмма разделили на три равные части докажите что

Геометрия 8 класс Атанасян Задачи 459-482

Упражнения 459-482 из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава VI. Площадь. § 2. Площади параллелограмма, треугольника и трапеции (52. Площадь параллелограмма. 53. Площадь треугольника. 54. Площадь трапеции). Геометрия 8 класс Атанасян Задачи 459-482 + ОТВЕТЫ.

Нажмите на спойлер, чтобы посмотреть ответ на задание.

Геометрия Атанасян. Глава 6.
§ 2. Площади параллелограмма,
треугольника и трапеции
Задачи №№ 459-482:

Задача № 460. Диагональ параллелограмма, равная 13 см, перпендикулярна к стороне параллелограмма, равной 12 см. Найдите площадь параллелограмма.

Задача № 461. Смежные стороны параллелограмма равны 12 см и 14 см, а его острый угол равен 30°. Найдите площадь параллелограмма.

Задача № 462. Сторона ромба равна 6 см, а один из углов равен 150°. Найдите площадь ромба.

Задача № 463. Сторона параллелограмма равна 8,1 см, а диагональ, равная 14 см, образует с ней угол в 30°. Найдите площадь параллелограмма.

Задача № 465. Острый угол параллелограмма равен 30°, а высоты, проведённые из вершины тупого угла, равны 2 см и 3 см. Найдите площадь параллелограмма.

Задача № 466. Диагональ параллелограмма равна его стороне. Найдите площадь параллелограмма, если большая его сторона равна 15,2 см, а один из его углов 45°.

Задача № 467. Квадрат и ромб, не являющийся квадратом, имеют одинаковые периметры. Сравните площади этих фигур.

Задача № 469. Стороны АВ и ВС треугольника АВС равны соответственно 16 см и 22 см, а высота, проведённая к стороне АВ, равна 11 см. Найдите высоту, проведённую к стороне ВС.

Задача № 470. Две стороны треугольника равны 7,5 см и 3,2 см. Высота, проведённая к большей стороне, равна 2,4 см. Найдите высоту, проведённую к меньшей из данных сторон.

Задача № 471. □ Найдите площадь прямоугольного треугольника, если его катеты равны: а) 4 см и 11 см; б) 1,2 дм и 3 дм.

Задача № 473. Через вершину С треугольника АВС проведена прямая m, параллельная стороне АВ. Докажите, что все треугольники с вершинами на прямой m и основанием АВ имеют равные площади.

Задача № 474. Сравните площади двух треугольников, на которые разделяется данный треугольник его медианой.

Задача № 475. □ Начертите треугольник АВС. Через вершину А проведите две прямые так, чтобы они разделили этот треугольник на три треугольника, имеющие равные площади.

Задача № 476. Докажите, что площадь ромба равна половине произведения его диагоналей. Вычислите площадь ромба, если его диагонали равны: а) 3,2 дм и 14 см; б) 4,6 дм и 2 дм.

Задача № 478. В выпуклом четырёхугольнике диагонали взаимно перпендикулярны. Докажите, что площадь четырёхугольника равна половине произведения его диагоналей.

Задача № 480. Найдите площадь трапеции ABCD с основаниями АВ и CD, если:
а) АВ = 21 см, CD = 17 см, высота ВН равна 7 см;
б) ∠D = 30°, АВ = 2 см, CD = 10 см, DA = 8 см;
в) ВС ⊥ АВ, АВ = 5 см, ВС = 8 см, CD = 13 см.

Задача № 481. Найдите площадь прямоугольной трапеции, у которой две меньшие стороны равны 6 см, а больший угол равен 135°.

Задача № 482. Тупой угол равнобедренной трапеции равен 135°, а высота, проведённая из вершины этого угла, делит большее основание на отрезки 1,4 см и 3,4 см. Найдите площадь трапеции.

Вы смотрели: Упражнения из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава VI. Площадь. § 2. Площади параллелограмма, треугольника и трапеции (52. Площадь параллелограмма. 53. Площадь треугольника. 54. Площадь трапеции). Геометрия 8 класс Атанасян Задачи 459-482 + ОТВЕТЫ.

Источник

Равновеликие фигуры

Презентация к уроку

Цели урока: Повторить тему «Площадь параллелограмма». Вывести формулу площади треугольник, ввести понятие равновеликих фигур. Решение задач по теме «Площади равновеликих фигур».

Ход урока

I. Повторение.

1) Устно по готовому чертежу вывести формулу площади параллелограмма.

2) Какова зависимость между сторонами параллелограмма и высотами, опущенными на них?

(по готовому чертежу)

зависимость обратно пропорциональная.

3) Найти вторую высоту (по готовому чертежу)

4) Найти площадь параллелограмма по готовому чертежу.

Решение:

5) Сравните площади параллелограммов S1, S2, S3. (Они имеют равные площади, у всех основание a и высота h).

Определение: Фигуры, имеющие равные площади, называются равновеликими.

II. Решение задач.

1) Доказать, что всякая прямая, проходящая через точку пересечения диагоналей, делит его на 2 равновеликие части.

Решение:

2) В параллелограмме ABCD CF и CE высоты. Доказать, что AD ∙ CF = AB ∙ CE.

3) Дана трапеция с основаниями a и 4a. Можно ли через одну из её вершин провести прямые, разбивающие трапецию на 5 равновеликих треугольников?

Решение: Можно. Все треугольники равновеликие.

4) Доказать, что если на стороне параллелограмма взять точку A и соединить её с вершинами, то площадь получившегося треугольника ABC равна половине площади параллелограмма.

Решение:

5) Торт имеет форму параллелограмма. Малыш и Карлсон делят его так: Малыш указывает на поверхности торта точку, а Карлсон по прямой, проходящей через эту точку, разрезает торт на 2 куска и один из кусков забирает себе. Каждый хочет получить кусок побольше. Где Малыш должен поставить точку?

Решение: В точке пересечения диагоналей.

6) На диагонали прямоугольника выбрали точку и провели через неё прямые, параллельные сторонам прямоугольника. По разные стороны образовались 2 прямоугольника. Сравните их площади.

Решение:

III. Изучение темы «Площадь треугольника»

«Найти площадь треугольника, у которого основание a, а высота h».

Ребята, используя понятие равновеликих фигур, доказывают теорему.

Достроим треугольник до параллелограмма.

Площадь треугольника равна половине площади параллелограмма.

Задание: Начертите равновеликие треугольники.

Используется модель (из бумаги вырезаны 3 цветных треугольника и склеены у оснований).

Упражнение №474. «Сравните площади двух треугольников, на которые разделяется данный треугольник его медианой».

У треугольников одинаковые основания a и одна и та же высота h. Треугольники имеют одинаковую площадь

Вывод: Фигуры, имеющие равные площади, называются равновеликими.

Вопросы к классу:

IV. Шаг вперёд!

На доске написаны задания по выбору:

1. «Разрежьте треугольник двумя прямыми линиями так, чтобы можно было из частей сложить прямоугольник».

Решение:

2. «Разрежьте прямоугольник по прямой линии на 2 части, из которых можно сложить прямоугольный треугольник».

Решение:

3) В прямоугольнике проведена диагональ. В одном из получившихся треугольников проведена медиана. Найдите соотношения между площадями фигур .

Решение:

Ответ:

3. Из олимпиадных задач:

«В четырёхугольнике ABCD точка E- середина AB, соединена с вершиной D, а F – середина CD, с вершиной B. Доказать, что площадь четырёхугольника EBFD в 2 раза меньше площади четырёхугольника ABCD.

Решение: провести диагональ BD.

Упражнение №475.

«Начертите треугольник ABC. Через вершину В проведите 2 прямые так, чтобы они разделили этот треугольник на 3 треугольника, имеющие равные площади».

Использовать теорему Фалеса (разделить АC на 3 равные части).

V. Задача дня.

Для неё отвела крайнюю правую часть доски, на которой пишу задачу сегодняшнего дня. Ребята могут решать её, а могут и не решать. На уроке данную задачу мы сегодня не решаем. Просто те, кому они интересны, могут списать её, решить её дома или в перемену. Обычно уже в перемену многие ребята начинают решать задачу, если решили, то показывают решение, и я фиксирую это в специальной таблице. На следующем уроке к этой задаче обязательно возвращаемся, уделяя её решению небольшую часть урока (а на доске может быть записана новая задача).

«В параллелограмме вырезан параллелограмм. Разделите оставшуюся часть на 2 равновеликие фигуры».

Решение: Секущая AB проходит через точку пересечения диагоналей параллелограммов O и O1.

Дополнительные задачи (из олимпиадных задач):

1) «В трапеции ABCD (AD || BC) вершины A и B соединены с точкой M – серединой стороны CD. Площадь треугольника ABM равна m. Найти площадь трапеции ABCD».

Решение:

Треугольники ABM и AMK – равновеликие фигуры, т.к. AM – медиана.
S_∆ABK = 2m, ∆BCM = ∆MDK, S_ABCD = S_∆ABK = 2m.

2) «В трапеции ABCD (AD || BC) диагонали пересекаются в точке O. Доказать, что треугольники AOB и COD равновеликие».

Решение:

S_∆BCD = S_∆ABC, т.к. у них общее основание BC и одинаковая высота.

3) Сторона АВ произвольного треугольника АВС продолжена за вершину В так, что ВР = АВ, сторону АС за вершину А так, что АМ = СА, сторону ВС за вершину С так, что КС = ВС. Во сколько раз площадь треугольника РМК больше площади треугольника АВС?

Решение:

В треугольнике МВС: МА = АС, значит, площадь треугольника ВАМ равна площади треугольника АВС. В треугольнике АРМ: ВР = АВ, значит, площадь треугольника ВАМ равна площади треугольника АВР. В треугольнике АРС: АВ = ВР, значит, площадь треугольника ВАС равна площади треугольника ВРС. В треугольнике ВРК: ВС = СК, значит, площадь треугольника ВРС равна площади треугольника РКС. В треугольнике АВК: ВС = СК, значит, площадь треугольника ВАС равна площади треугольника АСК. В треугольнике МСК: МА = АС, значит, площадь треугольника КАМ равна площади треугольника АСК. Получаем 7 равновеликих треугольников. Значит,

Ответ: Площадь треугольника МРК в 7 раз больше площади треугольника АВС.

4) Сцепленные параллелограммы.

2 параллелограмма расположены так, как показано на рисунке: они имеют общую вершину и ещё по одной вершине у каждого из параллелограммов лежит на сторонах другого параллелограмма. Доказать, что площади параллелограммов равны.

Решение:

и , значит,

Список использованной литературы:

Источник

Параллелограмм: свойства и признаки

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Определение параллелограмма

Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны. Как выглядит параллелограмм:

Частные случаи параллелограмма: ромб, прямоугольник, квадрат.

Диагонали — отрезки, которые соединяют противоположные вершины.

Свойства диагоналей параллелограмма:

Биссектриса параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.

Свойства биссектрисы параллелограмма:

Как найти площадь параллелограмма:

Периметр параллелограмма — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!

Свойства параллелограмма

Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.

Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:

А сейчас докажем теорему, которая основана на первых двух свойствах.

Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.

В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.

Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:

Теорема доказана. Наше предположение верно.

Признаки параллелограмма

Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.

Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.

Докажем 1 признак параллелограмма:

Шаг 1. Пусть в четырехугольнике ABCD:

Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.

Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.

Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:

Шаг 3. Из равенства треугольников также следует:

Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.

Вот так быстро мы доказали первый признак.

Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.

Докажем 2 признак параллелограмма:

Шаг 1. Пусть в четырехугольнике ABCD:

Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:

Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.

Шаг 3. Из равенства треугольников следует:

А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.

Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.

Доказали второй признак.

Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Докажем 3 признак параллелограмма:

Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:

Шаг 2. Из равенства треугольников следует, что CD = AB.

Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).

Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.

Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.

Источник

Срочно. Помогите пожалуйста: На диагоналях параллелограмма отмечены точки, которые делят каждую из диагоналей на три равные ча

Объяснение:проведи параллельные прямые, которые пересекаются эти точки и посчитай параллелограммы

Объяснение:

Смежные углы всегда в сумме равны 180°. Угол ABC на 20° больше угла CBD. Найдем угол CBD:

1) (180°-20°) : 2= 160°: 2= 80°- Угол CBD

2) 180°- 80°= 100°- угол ABC.

Треугольники DOC и АОВ подобны по первому признаку подобия треугольников: два угла одного треугольника соответственно равны двум углам другого. В нашем случае углы DOC и АОВ равны как вертикальные углы, а углы DCA и САВ равны как накрест лежащие углы при пересечении параллельных прямых DC и АВ секущей АС.
. Выразим ОС как 15-АО
. Поскольку треугольники подобны, можно записать:
АО / ОС = АВ / DC,
АО = ОС*АВ / DC
AO = (15-AO)*AB / DC
AO = (15-AO)*9.6 / 24
24AO = (15-AO)*9.6
24AO = 144 – 9.6AO
33.6AO = 144
AO = 144\33.6

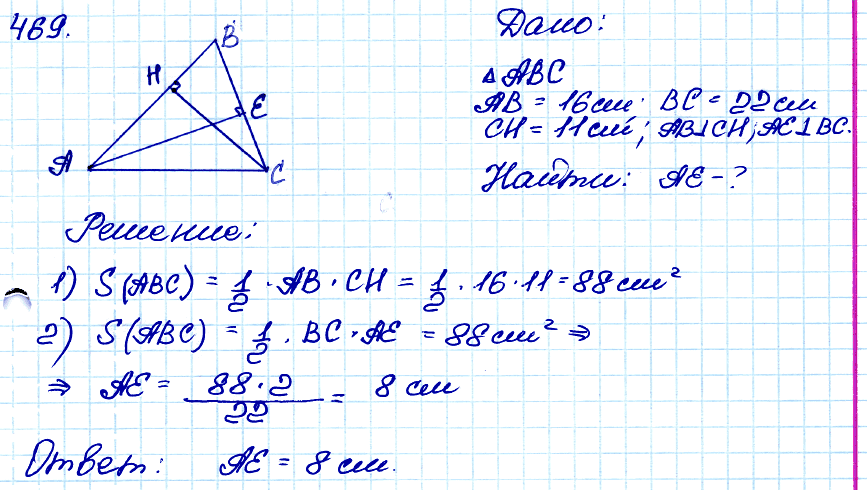
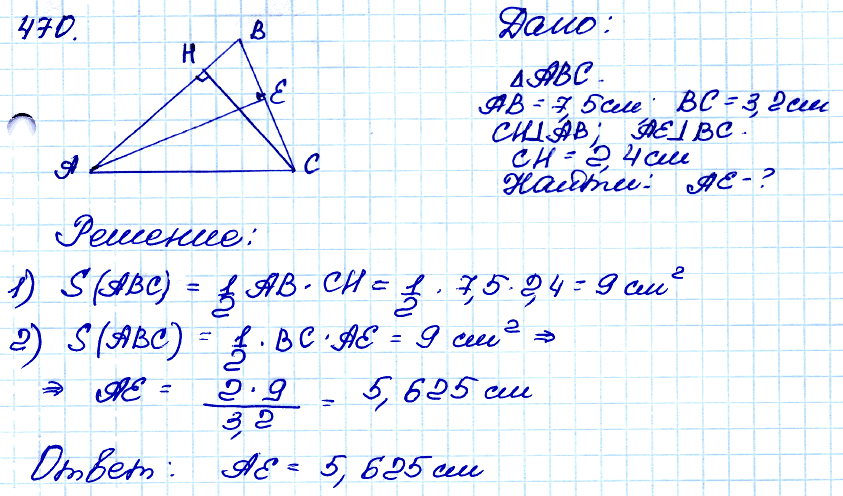
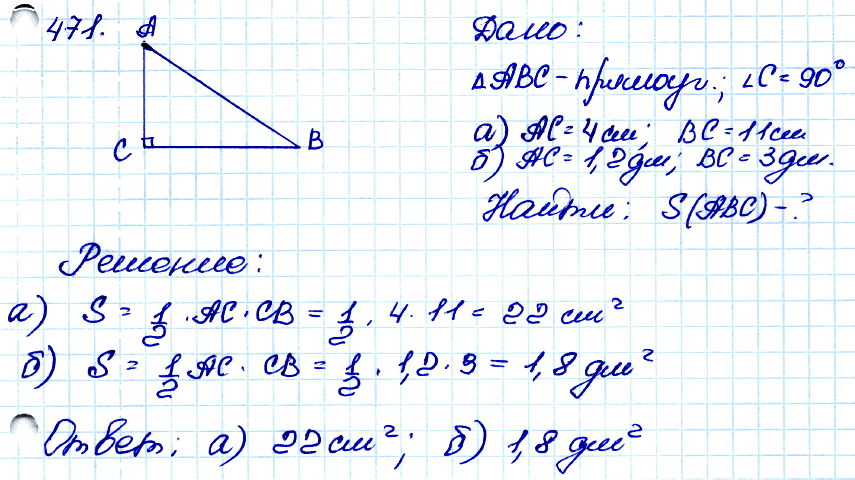
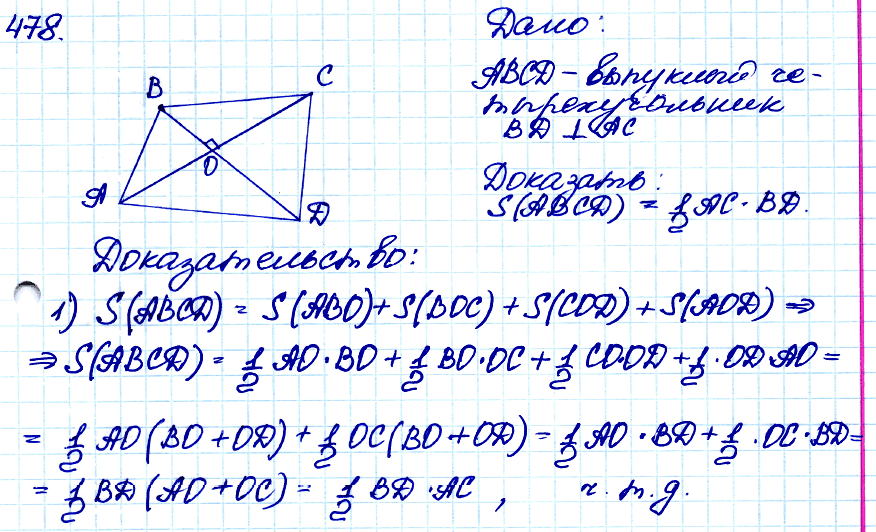
Источник