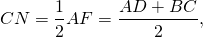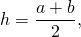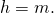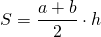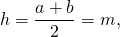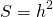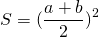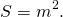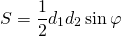Диагонали равнобедренной трапеции взаимно перпендикулярны докажите что расстояние между прямыми
Узнать ещё
Знание — сила. Познавательная информация
В равнобедренной трапеции диагонали перпендикулярны
Если в равнобедренной трапеции диагонали перпендикулярны, при решении задачи будет полезен следующий теоретический материал.
1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.
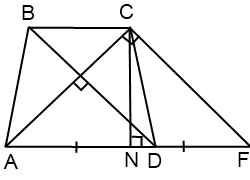
Проведем через точку C прямую CF, параллельную BD, и продлим прямую AD до пересечения с CF.
Четырехугольник BCFD — параллелограмм ( BC ∥ DF как основания трапеции, BD ∥ CF по построению). Значит, CF=BD, DF=BC и AF=AD+BC.
Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Поскольку в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF — равнобедренный с основанием AF. Значит, его высота CN является также медианой. А так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то
что в общем виде можно записать как
где h — высота трапеции, a и b — ее основания.
2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.
Так как средняя линия трапеции m равна полусумме оснований, то
3. Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высоты трапеции (или квадрату полусуммы оснований, или квадрату средней линии).
Так как площадь трапеции находится по формуле
а высота, полусумма оснований и средняя линия равнобокой трапеции с перпендикулярными диагоналями равны между собой:
4. Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле
sin 90 º =1, и диагонали равнобедренной трапеции равны, то площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна
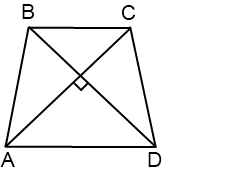
Диагонали равнобедренной трапеции АВСD взаимно перпендикулярны. Докажите, что расстояние между прямыми AD и ВС, содержащими
В 15:02 поступил вопрос в раздел ЕГЭ (школьный), который вызвал затруднения у обучающегося.
Вопрос вызвавший трудности
Ответ подготовленный экспертами Учись.Ru
Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике «ЕГЭ (школьный)». Ваш вопрос звучал следующим образом: Диагонали равнобедренной трапеции АВСD взаимно перпендикулярны. Докажите, что расстояние между прямыми AD и ВС, содержащими основания, равно 1/2(AD + BC).
После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:
решение задания по геометрии
НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:
Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.
ПОМОГАЕМ УЧИТЬСЯ НА ОТЛИЧНО!
Выполняем ученические работы любой сложности на заказ. Гарантируем низкие цены и высокое качество.
Деятельность компании в цифрах:
Зачтено оказывает услуги помощи студентам с 1999 года. За все время деятельности мы выполнили более 400 тысяч работ. Написанные нами работы все были успешно защищены и сданы. К настоящему моменту наши офисы работают в 40 городах.
Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.
Диагонали равнобедренной трапеции взаимно перпендикулярны докажите что расстояние между прямыми
Напомним свойства трапеции, которые часто используются при решении задач. Некоторые из этих свойств были доказаны в заданиях для 9-го класса, другие попробуйте доказать самостоятельно. Приведённые рисунки напоминают ход доказательства.
$$ 4.<2>^<○>$$. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжении боковых сторон, лежат на одной прямой (на рис. 21 точки `M`, `N`, `O` и `K`).
$$ 4.<3>^<○>$$. В равнобокой трапеции углы при основании равны (рис. 22).
$$ 4.<4>^<○>$$. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции (рис. 23).
$$ 4.<5>^<○>$$. В равнобокой трапеции диагонали равны (рис. 24).
$$ 4.<6>^<○>$$. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой – их полусумме
(рис. 25, основания равны `a` и `b`, `a>b`).
$$ 4.<7>^<○>$$. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой (рис. 26).
$$ 4.<8>^<○>$$. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований (рис. 27).
Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований, т. е. `d_1^2+d_2^2=c_1^2+c_2^2+2*ab`.
$$ 4.<10>^<○>$$. Во всякой трапеции с основаниями `a` и `b` отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен `(2ab)/(a+b)` (на рис. 28 отрезок `MN`).
$$ 4.<11>^<○>$$. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.
Применяем теорему косинусов (см. рис. 29а и б):
`ul(DeltaACD):` `d_1^2=a^2+c_2^2-2a*c_2*cos varphi`,
`ul(DeltaBCD):` `d_2^2=b^2+c_2^2+2b*c_2*cos varphi` (т. к. `cos(180^@-varphi)=-cos varphi`).
Проводим `CK«|\|«BA` (рис. 29в), рассматриваем треугольник `ul(KCD):` `c_1^2=c_2^2+(a-b)^2-2c_2*(a-b)*cos varphi`. Используя последнее равенство, заменяем выражение в скобках в (2), получаем:
| `d_1^2+d_2^2=c_1^2+c_2^2+2ab`. |
В случае равнобокой трапеции `d_1=d_2`, `c_1=c_2=c`, поэтому получаем
Отрезок, соединяющий середины оснований трапеции, равен `5`, одна из диагоналей равна `6`. Найти площадь трапеции, если её диагонали перпендикулярны.
Прямоугольный треугольник `ul(BDK)` с гипотенузой `BK=BC+AD=2MN=10` и катетом `DK=6` имеет площадь `S=1/2DK*BD=1/2DKsqrt(BK^2-DK^2)=24`. Но площадь треугольника `BDK` равна площади трапеции, т. к. если `DP_|_BK`, то
Диагонали трапеции, пересекаясь, разбивают её на четыре треугольника с общей вершиной. Найти площадь трапеции, если площади треугольников, прилежащих к основаниям, равны `S_1` и `S_2`.
Далее, треугольники `BOC` и `DOA` подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит, `(S_1)/(S_2)=(a/b)^2`. Таким образом, `(S_0+S_1)/(S_0+S_2)=sqrt((S_1)/(S_2))`.Отсюда находим `S_0=sqrt(S_1S_2)`, и поэтому площадь трапеции будет равна
Основания равнобокой трапеции равны `8` и `10`, высота трапеции равна `3` (рис. 32).
Найти радиус окружности, описанной около этой трапеции.
Из прямоугольного треугольника `ABK` находим `AB=sqrt(1+9)=sqrt(10)` и `sinA=(BK)/(AB)=3/(sqrt10)`. Окружность, описанная около трапеции `ABCD`, описана и около треугольника `ABD`, значит (формула (1), § 1), `R=(BD)/(2sinA)`. Отрезок `BD` находим из прямоугольного треугольника `KDB:` `BD=sqrt(BK^2+KD^2)=3sqrt(10)` (или по формуле `d^2=c^2+ab`), тогда
$$ 4.<12>^<○>$$. Площадь трапеции равна площади треугольника, две стороны которого равны диагоналям трапеции, а третья равна сумме оснований.
Диагонали равнобедренной трапеции ABCD взаимно перпендикулярны?
Диагонали равнобедренной трапеции ABCD взаимно перпендикулярны.
Диагонали образуют с основаниями 2 равнобедренных прямоугольных треугольника.
Диагонали равнобедренной трапеции взаимно перпендикулярны?
Диагонали равнобедренной трапеции взаимно перпендикулярны.
Найти площадь, если основания равны 12 и 16 см.
Диагонали равнобедренной трапеции взаимно перпендикулярны?
Диагонали равнобедренной трапеции взаимно перпендикулярны.
Основания равны 24см и 40см.
Вычислите ее площадь.
Чему равна высота трапеции?
Диагонали равнобедренной трапеции взаимно перпендикулярны?
Диагонали равнобедренной трапеции взаимно перпендикулярны.
Докажите, что средняя линия трапеции равна высоте.
НАЙДИТЕ ОСНОВАНИЯ ТРАПЕЦИЙ 2)ДИАГОНАЛИ РАВНОБЕДРЕННОЙ ТРАПЕЦИИ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫ.
Помогите пожалуйста плыыз?
Помогите пожалуйста плыыз!
1)разность оснований трапеции равна 6 см, её средняя линия равна 15см.
Найдите основания трапеции 2)Диагонали равнобедренной трапеции взаимно перпендикулярны.
Докажите, что расстояние между прямыми, содержащими основания, равно длине средней линии трапеции.
Докажите, что если в равнобедренной трапеции высота равна средней линии, то диагонали трапеции взаимно перпендикулярны?
Докажите, что если в равнобедренной трапеции высота равна средней линии, то диагонали трапеции взаимно перпендикулярны.
Диагонали равнобедренной трапеции взаимно перпендикулярны?
Диагонали равнобедренной трапеции взаимно перпендикулярны.
Основания равны 24и40см.
Найдите её площадь.
В равнобедренной трапеции ABCD диагонали взаимно перпендикулярны?
В равнобедренной трапеции ABCD диагонали взаимно перпендикулярны.
Найдите площадь трапеции, если диагональ AC равна 6см.
По теореме Пифагора a ^ 2 + b ^ 2 = c ^ 2 c ^ 2 = 60 ^ 2 * 90 ^ 2 c = корень из 11700 с = 30 корень из 13.
Так как пирамида правильная, в основании лежит равносторонний треугольник, значит ребро основания равно 12 : 3 = 4 см. Боковая грань это равнобдренный треугольник, его площадь равна половина произведения основания на высоту, а высота в этом треуголь..
S = 1 / 2ab * sin угла между ними S = 1 / 2 * 8 * 8 (у р / б треугольника боковые стороны равны) * sin 135 S = 1 / 2 * 64 * (√2 / 2) = 32 * √2 : 2 = 16√2.
Периметр 2 * 4 + 2 * 2 = 12 Площадь 4 * 3 = 12.
Биссектриса треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам : ВС / 144 = 36 / 48 = 3 / 4 ; ВС = 3 * 144 / 4 = 108.
Он равен самому числу без знаков.
Диагонали равнобедренной трапеции взаимно перпендикулярны докажите что расстояние между прямыми
Дана трапеция с диагоналями равными 6 и 8. Сумма оснований равна 10.
а) Докажите, что диагонали перпендикулярны.
б) Найдите высоту трапеции.
а) Проведем через точку прямую параллельную
На пересечении этой прямой и прямой
отметим точку
— параллелограмм.
В треугольнике ACC1:
Заметим, что поскольку
тогда по теореме, обратной теореме Пифагора, треугольник ACC1 — прямоугольный, угол ACC1 прямой. Тогда угол COD прямой, что и требовалось доказать.
б) Высота трапеции равна
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |
Аналоги к заданию № 517526: 517528 517535 Все