Динамическая нагрузка в чем измеряется
Динамические нагрузки
Динамическая нагрузка — нагрузка, характеризующаяся быстрым изменением во времени её значения, направления или точки приложения и вызывающая в элементах конструкции значительные силы инерции.
Статическая нагрузка — нагрузка, величина, направление и точка приложения которой изменяются во времени незначительно. При прочностных расчетах можно пренебречь влиянием сил инерции, обусловленных такой нагрузкой. Статической нагрузкой, например, является вес сооружения.
См. также
Смотреть что такое «Динамические нагрузки» в других словарях:
испытание на динамические нагрузки — rus испытание (с) на динамические нагрузки eng drop test (safety belt) fra essai (m) de chute deu Fallversuch (m) spa prueba (f) de caída … Безопасность и гигиена труда. Перевод на английский, французский, немецкий, испанский языки
Нагрузки — – внешние механические силы (вес конструкций, оборудования, снегоотложений, людей и т. п.), действующие на строительные объекты. [СНиП 2.01.07 85] Нагрузки – силовые воздействия, вызывающие изменения напряжённо деформированного… … Энциклопедия терминов, определений и пояснений строительных материалов
НАГРУЗКИ — в строительной механике силовые воздействия, вызывающие изменения напряжённо деформиров. состояния конструкций зданий и сооружений. По характеру изменений во времени различают статические нагрузки и динамические нагрузки. Статич. Н.… … Большой энциклопедический политехнический словарь
Нагрузки на летательный аппарат — система сил, действующих на летательный аппарат и являющихся основой для определения его прочности. В эту систему входят аэродинамические, аэростатические, инерционные силы, тяга двигателей, силы от реакции земли при движении по аэродрому, от… … Энциклопедия техники
НАГРУЗКИ — в строительной механике внешние воздействия на сооружение (статические и динамические, постоянные и временные), вызывающие деформации и изменение напряженного состояния в его элементах. Помимо внешних нагрузок (снеговых, ветровых, технологических … Большой Энциклопедический словарь
нагрузки — (в строительной механике), внешние воздействия на сооружение (статические и динамические, постоянные и временные), вызывающие деформации и изменение напряжённого состояния в его элементах. Помимо внешней нагрузки (снеговых, ветровых,… … Энциклопедический словарь
нагрузки на летательный аппарат — Рис. 1. Распределение вертикальных проекций аэродинамических нагрузок на самолёт. нагрузки на летательный аппарат система сил, действующих на летательный аппарат и являющихся основой для определения его прочности. В эту систему входят… … Энциклопедия «Авиация»
нагрузки на летательный аппарат — Рис. 1. Распределение вертикальных проекций аэродинамических нагрузок на самолёт. нагрузки на летательный аппарат система сил, действующих на летательный аппарат и являющихся основой для определения его прочности. В эту систему входят… … Энциклопедия «Авиация»
Нагрузки — в строительной механике, силовые воздействия, вызывающие изменение напряжённо деформированного состояния конструкций зданий и сооружений. По характеру изменений во времени различают Н. статические, местоприложения, направление и… … Большая советская энциклопедия
динамические испытания — [dynamic tests] испытания материалов при скоростях деформирования и приложения нагрузки, существенно превышающих скорости при обычных статических испытаниях. В России динамическим принято считать нагружение при перемещении активного захвата со… … Энциклопедический словарь по металлургии
Нагрузки (виды нагрузок, единицы измерения нагрузок).
Нагрузки (виды нагрузок, единицы измерения нагрузок).
Нагрузки – это внешние силы, действующие на конструкцию.
Сила – это мера механического воздействия одного тела на другое.
Единица измерения – ньютон (Н).
Также приблизительно можно принять:
1тонна =1000кг =10000Н =10кН
а) По длительности воздействия – постоянные, временные, переменные.
Б) По характеру приложения – распределённые и сосредоточенные.
В) По характеру воздействия – статические и динамические.
Статическая нагрузка медленно возрастает от нуля до своего конечного значения и остаётся постоянной в процессе работы детали или конструкции.
Динамическая нагрузка мгновенно возрастает от нуля до своего конечного значения и её значение непостоянно в процессе работы детали или конструкции.
Расчетные схемы.
При расчётах в сопромате для упрощения графической части реальные конструкции заменяются расчётными схемами, т.е. вместо чертежа детали или конструкции изображают упрощённую схему и по ней проводят расчёты.
Внутренние силовые факторы, метод сечений.
При действии на тело внешних сил внутри тела возникают силы сопротивления, которые называются внутренними силовыми факторами.
При различных видах деформаций возникают определённые внутренние силовые факторы. Всего при различных видах деформаций возникает шесть внутренних силовых факторов, которые характеризуют все виды деформаций, существующие в природе.
1. N – продольная сила, возникает при деформации растяжение и сжатие.
Это поперечные силы, возникают при деформации сдвиг.
Это изгибающие моменты, возникают при деформации изгиб.
6. МZ =Т – крутящий момент, возникает при деформации кручение.
Чтобы вычислить внутренние силовые факторы, применяется метод сечений, который заключается в том, что тело мысленно рассекается на две части, одна часть отбрасывается, а другая рассматривается и вместо отброшенной части прикладываются внутренние силовые факторы. Значения внутренних силовых факторов вычисляются из уравнений равновесия.
Напряжение.
Нормальное напряжение.
Касательное напряжение.
Напряжение – это мера интенсивности действия внутренних сил.
При действии на конструкцию внешней нагрузки в материале конструкции возникает механическое напряжение, которое характеризует интенсивность внутренних сил. Если нагрузку постепенно увеличивать, то значение напряжения тоже будет увеличиваться, и когда оно достигнет какого – то критического значения, произойдёт разрушение материала.
Полное напряжение р разложим на две оси, одна из них перпендикулярна к поперечному сечению конструкции, другая параллельна.
σ – нормальное напряжение, возникает при деформации растяжение или сжатие, всегда направлено перпендикулярно к поперечному сечению конструкции.
τ – касательное напряжение, возникает при деформации сдвиг, всегда направлено параллельно к поперечному сечению конструкции.
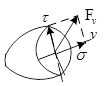
Рассмотрим нормальное напряжение. Оно вычисляется по следующей формуле:
где S – площадь поперечного сечения конструкции
Единица измерения напряжения (Н/м2 ) =Па
Так как величина Па очень маленькая, то на практике применяют величину
[σ] – допускаемое нормальное напряжение, каждый материал имеет своё значение.
Чтобы обеспечить прочность конструкции, значение напряжения не должно превышать допускаемого, иначе может произойти разрушение материала.
Приблизительные значения допускаемого нормального напряжения для некоторых материалов:
Алюминий: [σ] = 30…100 МПа
Сталь 45: [σ] = 240…360 МПа
Легированные высококачественные стали: [σ] = 400 МПа и выше
Вольфрам: [σ] = 500 МПа
Рассмотрим касательное напряжение. Оно вычисляется по следующей формуле:
[τ] – допускаемое касательное напряжение, каждый материал имеет своё значение.
Для большинства материалов [τ] = 0,6•[σ]
Деформации и перемещения.
Деформация – это изменение формы и объёма тела.
Деформация бывает упругой и пластичной. При упругой деформации тело полностью восстанавливает свою первоначальную форму и размеры после снятия нагрузки, а при пластичной нагрузке этого не происходит.
Деформация также бывает линейной и угловой.
Расчёт на прочность при растяжении и сжатии.
Условие прочности при растяжении и сжатии – нормальное напряжение не должно превышать допускаемого значения.
Основное уравнение прочности при растяжении и сжатии выглядит следующим образом:
Расчёт на прочность при растяжении и сжатии можно также проводить через коэффициент запаса прочности
n – коэффициент запаса прочности
[n] – минимально допустимый коэффициент запаса прочности
При статической нагрузке [n] =1,5
Чтобы обеспечить прочность, должно соблюдаться условие:
Температурные напряжения.
При нагреве или охлаждении металлического стержня его длина изменяется. Удлинение от действия температуры вычисляется по формуле
где α – коэффициент температурного расширения, величина табличная.
Например, для стали α = 1,25·10 – 5 1/град
Δt – изменение температуры
В связи с нагревом или охлаждением в металлических конструкциях могут возникнуть дополнительные температурные напряжения. Вычислив удлинение от действия температуры, из формулы (3) можно вычислить температурные напряжения.
Монтажные напряжения.
Часто встречаются случаи, когда стержневые элементы конструкций изготавливаются короче или длиннее проектной длины. При монтаже конструкции такие стержни приходится растягивать или укорачивать, что приводит к возникновению дополнительных монтажных напряжений. Эти напряжения можно вычислить из формулы (3).
16. Сдвиг (основные понятия и определения), расчёт на прочность при сдвиге.
Сдвиг – это такой вид деформации, при котором в поперечном сечении бруса возникает следующий внутренний силовой фактор – поперечная сила Q.
Деформация сдвиг ещё называется срез.
При сдвиге действует касательное напряжения τ, которое вычисляется по следующей формуле
Деформация при сдвиге называется углом сдвига γ, вычисляется по следующей формуле
где G – модуль упругости ΙΙ рода, или модуль сдвига, характеризует жесткость бруса при сдвиге, величина табличная.
Для большинства материалов G = 0,4•E
Величина GS называется жёсткостью при сдвиге.
Подставим выражение (7) в выражение (8), получим
Выражения (9) и (10) являются законом Гука при сдвиге, который формулируется следующим образом: напряжение прямо пропорционально углу сдвига.
Единица измерения угла сдвига – радиан, можно перевести в градусы.
Условие прочности при сдвиге – касательное напряжение не должно превышать допускаемого значения.
Основное уравнение прочности при сдвиге выглядит следующим образом:
Примеры расчёта конструкций, работающих на сдвиг.
Рассмотрим заклёпочное соединение, на которое действуют сила F, направленная перпендикулярно осям заклёпок.
Условие прочности такого соединения имеет вид:
В данном случае Q =F;
S – площадь поперечного сечения всех заклёпок;
где S1 – площадь поперечного сечения одной заклёпки
Рассмотрим сварное соединение внахлёстку, на которое действует сила F.
Условие прочности такого соединения имеет вид:
В данном случае Q =F;
S – расчётная площадь сварного шва
где k – катет сварного шва
L – длина сварного шва по длине соединения
b – длина сварного шва по ширине соединения
Кинематические пары.
Примеры кинематических пар в зависимости от классов.
Кинематическая пара – соединение двух соприкасающихся звеньев, допускающее их относительное движение.
Элемент кинематическая пары – совокупность поверхностей, линий и отдельных точек звена, по которым оно может соприкасаться с другим звеном, образуя кинематическую пару
Кинематические пары различают и классифицируют по различным признакам.
1) По числу связей, налагаемых на относительное движение звеньев.
Всякое свободно движущееся в пространстве абсолютно твердое тело обладает шестью степенями свободы или шестью видами независимых возможных движений. Вхождение двух звеньев в кинематическую пару налагает на их относительное движение некоторые ограничения или условия связи; класс кинематической пары (номер класса совпадает с числом условий связи S) всегда находится в пределах от 1 до 5, число оставшихся подвижностей H дополняет число связей до шести, т.е. 
На рис. 3 представлены примеры кинематических пар 1 – 5 классов.
2) По характеру контакта звеньев различают пары низшие (требуемое относительное движение звеньев можно получить постоянным соприкасанием их элементов по поверхности) и высшие (требуемое относительное движение можно получить только соприкасанием их элементов по линиям и в точках). Например, трехподвижная пара по
рис. 3, в – низшая, а четырехподвижная по рис. 3, б – высшая.
3) По области относительного движения звеньев пары могут быть плоскими (траектории всех точек в относительном движении звеньев – плоские кривые, расположенные в параллельных плоскостях) и пространственными.
Плоская одноподвижная пара может быть либо вращательной (шарниром – рис. 3, д), либо поступательной (рис. 3, е); пространственная пара может быть, например, винтовой (одноподвижная), цилиндрической (двухподвижная), сферической (двух- и трехподвижная) и т.д.
Механизм, звенья которого образуют только вращательные, поступательные, цилиндрические и сферические пары, называют рычажным.
 |  |
| а – пятиподвижная пара (1 класс) | б – четырехподвижная пара (2 класс) |
 |  |
| в – трехподвижная пара (3 класс) | г – двухподвижная пара (4 класс) |
 |  |
| д – одноподвижная вращательная пара (5 класс) | е – одноподвижная поступательная пара (5 класс) |
| Рис. 3 |
Кинематические цепи.
Систему звеньев, связанных между собой кинематическими парами, называют кинематической цепью.
Классификация кинематических цепей
1) По области движения звеньев цепи бывают плоские (траектории движения точек всех звеньев –– плоские кривые, лежащие в параллельных плоскостях) и пространственные.
2) По признаку наличия разветвлений различают цепи простые (каждое звено цепи входит не более, чем в две кинематических пары) и сложные или разветвленные (некоторые звенья входят в три, или более пары); в разветвленных цепях могут присутствовать так называемые кратные (двойные, тройные и т.д.) шарниры.
3) По признаку наличия в кинематических цепях замкнутых контуров цепи могут быть замкнутыми и незамкнутыми; в замкнутой цепи каждое звено входит не менее, чем в две кинематические пары.
Некоторые дополнительные определения:
обобщенная координата механизма – каждая из независимых координат, определяющих положение всех звеньев механизма относительно стойки;
число степеней свободы (степень подвижности) механизма – число независимых вариаций обобщенных координат механизма;
начальное звено – звено, которому приписывается одна или несколько обобщенных координат механизма;
входное звено – звено, которому сообщается движение, преобразуемое механизмом в требуемые движения других звеньев;
выходное звено – звено, совершающее движение, для выполнения которого предназначен механизм.
Примеры.
Методы силового анализа.
Силовой расчет механизмов без учета трения в кинематических парах допускает применение как аналитических, так и графо – аналитических методов.
В настоящем пособии предпочтение отдано графо – аналитическому методу планов сил.
Поскольку векторный план представляет собой графическое изображение векторного равенства, то при простой форме векторных силовых многоугольников их аналитическая обработка достаточно проста и позволяет рассчитать точные силовые соотношения для заданных положений механизмов.
Нагрузки (виды нагрузок, единицы измерения нагрузок).
Нагрузки – это внешние силы, действующие на конструкцию.
Сила – это мера механического воздействия одного тела на другое.
Единица измерения – ньютон (Н).
Также приблизительно можно принять:
1тонна =1000кг =10000Н =10кН
а) По длительности воздействия – постоянные, временные, переменные.
Б) По характеру приложения – распределённые и сосредоточенные.
В) По характеру воздействия – статические и динамические.
Статическая нагрузка медленно возрастает от нуля до своего конечного значения и остаётся постоянной в процессе работы детали или конструкции.
Динамическая нагрузка мгновенно возрастает от нуля до своего конечного значения и её значение непостоянно в процессе работы детали или конструкции.
Расчетные схемы.
При расчётах в сопромате для упрощения графической части реальные конструкции заменяются расчётными схемами, т.е. вместо чертежа детали или конструкции изображают упрощённую схему и по ней проводят расчёты.
Виды нагрузок или в чем сила, сопромат?
В данном случае имеются в виду физические силы, а всякие там силы духа, мысли, третьего глаза и тому подобные не рассматриваются. Во всяком случае до тех пор, пока телепаты и экстрасенсы не начнут вместо подъемных механизмов работать на стойках народного хозяйства, силой мысли перемещая панели и плиты перекрытия, а не ложки и стаканы в различных телешоу.
Нагрузками, наиболее часто рассматриваемыми при расчете строительных конструкций, являются массы тел (причем далеко не всегда только физическая масса, а иногда еще и инерционная, но об этом чуть позже) и разница давлений. Но это далеко не все, что можно сказать о нагрузках.
В теоретической механике и сопромате принято различать нагрузки, действующие на рассчитываемые конструкции или элементы конструкций, по различным признакам. Одним из таких признаков является время действия нагрузки. По времени действия нагрузки делятся на постоянные и временные:
Постоянные нагрузки
Нагрузки, действующие на конструкцию в течение всего времени эксплуатации конструкции, будь то одна секунда или одно тысячелетие.
Временные нагрузки
Это все остальные нагрузки, действующие на конструкцию.
В свою очередь временные нагрузки принято разделять на длительные и кратковременные:
Длительные нагрузки
Кратковременные нагрузки
Для более точного определения нагрузки дополнительно разделяются на статические и динамические.
Статические нагрузки
Условно говоря, это силы, приложенные с минимальным ускорением или с ускорением, стремящимся к нулю.
Таким образом действие инерционной силы при столь малых ускорениях стремится к нулю и расчет ведется только на действие силы от физической массы. Или так: При воздействии статических нагрузок происходит относительно медленное нарастание деформаций, и потому инерционными массами отдельных элементов конструкции, перемещающихся в процессе деформации, можно пренебречь, так как ускорения таких перемещений являются незначительными. В результате этого равновесие между внешними и внутренними силами в любой момент действия статической нагрузки остается как бы неизменным.
К статическим относятся постоянные и длительные нагрузки, иногда кратковременные нагрузки.
Динамические нагрузки
Это нагрузки, изменяющиеся не только во времени, но и в пространстве.
Для динамических нагрузок характерна относительно большая скорость приложения, что требует при расчетах учитывать инерционную массу как объекта, создающего нагрузку, так и элемента, подвергающегося воздействию нагрузки. Другими словами, следует учитывать характер движения объекта создающего нагрузку, а также то, что инерционные массы элементов конструкции, подвергающиеся воздействию динамической нагрузки, перемещаются с ускорением и влияют на напряженно-деформированное состояние элементов. Чтобы учесть это влияние, в уравнения статического равновесия к внешним и внутренним силам добавляются силы инерции на основании принципа Даламбера. Добавление инерционных сил позволяет рассматривать любую движущуюся систему как находящуюся в состоянии статического равновесия в любой момент времени. Таким образом динамические нагрузки вызывают в материале исследуемого элемента конструкции динамические напряжения и поведение материала при этом оказывается отличным от поведения при статических напряжениях.
В свою очередь динамические нагрузки в зависимости от характера движения бывают также нескольких видов. Для строительных конструкций наиболее важными являются подвижные и ударные нагрузки:
Подвижные нагрузки
Это нагрузки возникающие в результате перемещения некоего объекта по поверхности исследуемой конструкции (вдоль рассматриваемой оси элемента).
Ударные нагрузки
Это нагрузки, возникающие в момент соприкосновения перемещающегося объекта с поверхностью исследуемой конструкции (вдоль или поперек рассматриваемой оси элемента).
Однако и это еще не все варианты классификации нагрузок. По площади приложения нагрузки делятся на сосредоточенные и распределенные.
Сосредоточенные нагрузки
Это силы, площадь приложения которых пренебрежимо мала по сравнению с площадью рассчитываемой конструкции.
Распределенные нагрузки
Это все остальные нагрузки, т.е. силы, распределяющиеся по длине и ширине элемента.
Разнообразие распределенных нагрузок поистине не поддается описанию. Распределенные нагрузки могут равномерно и неравномерно распределенными, равномерно и неравномерно изменяющимися по длине или ширине, при этом характер изменения нагрузки может описываться уравнением параболы, синусоиды, окружности, овала и любым другим уравнением.
А самое примечательное во всем этом то, что один и тот же человек в зависимости от ситуации может рассматриваться и как сосредоточенная нагрузка и как распределенная, и как статическая и как динамическая и только постоянной нагрузкой человек быть не может.
В целом все это выглядит не совсем понятно, однако ничего страшного в этом нет, как говорится, лучше один раз рассчитать конструкцию, чем 100 раз прочитать, как это делается. Примеров расчета на сайте хватает. А кроме того, понимание основ сопромата позволяет в большинстве случаев определять нагрузки так, чтобы максимально упростить расчет.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).
Виды динамических нагрузок и характеристики колебаний
Многие строительные конструкции, кроме статических, воспринимают и динамические нагрузки, сообщающие их массам ускорения и вызывающие появление инерционных сил и колебаний.
К динамическим относятся нагрузки, изменяющие свою величину, направление или место приложения на конструкции. Их можно разделить на ряд видов:
1. Неподвижная нагрузка, действующая постоянно или периодически изменяющая свою величину н частоту. Например, токарные и ткацкие станки, типографские машины, различные двигатели, вентиляторы, компрессоры, грохоты, пилорамы, вибрационные машины и другое стационарное оборудование (рис. 8.1, а).
2. Подвижная нагрузка, меняющая свое положение на конструкции. Передается от мостовых кранов, рельсового или автомобильного транспорта (рис. 8.1, б).
3.Импульсная нагрузка, действующая на конструкцию в течение достаточно малого промежутка времени в результате взрыва, внезапного изменения давления газа или жидкости в трубопроводах или резервуарах, при включении, выключении или коротком замыкании электромашин и т. д. (рис. 8.1, в).
4. Ударная нагрузка, создающаяся падающими телами, копрами, молотами и другими механизмами ударного действия (рис. 8.1, г),звуковыми ударными волнами при полетах сверхзвуковых самолетов.
5. Динамическая составляющая ветровой нагрузки, вызванная пульсацией скоростного напора, учитывается при расчете высотных сооружений с периодом собственных колебаний более 0,25 с, например многоэтажных зданий высотой более 40 м, одноэтажных однопролетных производственных зданий высотой более 36 м, открытых этажерок, транспортных галерей, мачт, башен, дымовых труб, опор линий электропередач и других сооружений (рис. 8.1, д).
6. Сейсмическая нагрузка, проявляющаяся в виде беспорядочных смещений и колебаний почвы, толчков и ударов при землетрясении (рис. 8.1, е).
7. Комбинированная нагрузка, состоящая из нескольких видов динамических воздействий, на пример от групповых динамических воздействий большого количества машин с синхронным или асинхронным приводом.
Таким образом, динамическая нагрузка вызывается работой машин и оборудования с неуравновешенными массами, транспортными средствами, взрывами и ударами, порывами ветра, морской волны, сейсмическими и другими воздействиями. В строительных конструкциях под действием динамических нагрузок возникают колебания, перемещения и деформации, усилия и напряжения. Причем, если результат воздействия статической нагрузки определяется величиной, влияние динамической нагрузки оценивается не только ее величиной, но прежде всего характером воздействия.
При этом приходится считаться: с разрушительным действием вибрации на конструкцию в связи с усталостным снижением прочности материала; с динамической устойчивостью сооружения или грунта основания; с вредным влиянием вибраций на организм людей и нормальную работу технологического оборудования.
Рис. 8.2. Виброграмма затухающих колебаний
энергии имеет затухающий характер (рис. 8.2). Время полного цикла 




откуда коэффициент затухания
Затухание колебаний связано с затратой энергии на преодоление внешних и внутренних сопротивлений. Внешние сопротивления обусловлены силами трения в опорных закреплениях и узловых сопряжениях, сопротивлением воздушной среды и другими факторами.
Рис.8.3. Диаграмма работы материалов:
Внутренние сопротивления обусловлены в основном пластическими деформациями материала. Зависимость между внешней силой и перемещениями материала показана на рис. 8.3. Площадь замкнутой петли гистерезиса пропорциональна работе 

При экспериментальном определении коэффициента поглощения энергии для повышения точности виброграмму разбивают па несколько участков по 
В расчетах вместо коэффициента поглощения энергии часто пользуются пропорциональным ему параметром, называемым коэффициентом неупругого сопротивления:
Значение коэффициента 
Рис. 8.4. Максимальные 

средние 

Категория динамической нагрузки устанавливается в зависимости от величины и характера внешнего воздействия. К I и II категориям относятся слабые и умеренные импульсы 


Вынужденными называются колебания, вызываемые внешней возмущающей силой при ее непрерывном воздействии. При таких колебаниях системе непрерывно сообщается энергия со стороны действующей силы. Часть этой энергии затрачивается на преодоление внешних и внутренних сопротивлений, оставшаяся вызывает колебания, которые не затухают, пока действует возмущающая сила (рис. 8.4). Период вынужденных колебаний равен периоду возмущающей силы. Амплитуда от начальных условий не зависит. Частота возмущающей силы может быть и переменной во времени. Когда частота возмущающей силы близки или совпадает с частотой собственных колебаний конструкции, происходит резкое увеличение амплитуды (рис. 8.5, а), что связано с явлением резонанса. Если частота возмущающей силы изменяется, резонанс прекращается. При резонансе возникают недопустимые для нормальной работы конструкции перемещения и деформации, которые могут вывести ее из строя. Известен случай разрушения вантового моста через залив Такома в США от чрезмерных колебаний пролетного строения, вызванных ветром. Для высотных гибких сооружений типа мачт, дымовых труб производят поверочный расчет на резонанс, который возможен при таких скоростях, когда частота срыва вихрей совпадает с собственной частотой колебаний сооружения. Когда частоты вынужденных колебаний становятся кратными частотам собственных колебаний, наблюдается частичный резонанс в менее выраженной форме. Резонанс следует отличать от биения (рис. 8.5, б), когда на конструкцию действуют две силы с весьма близкими частотами. Если какой-либо из параметров конструкции, например масса или жесткость, периодически изменяется при действии внешней возмущающей силы, такие колебания называют параметрическими. Они возникают, например, при вращении вала некруглого сечения с переменной жесткостью.
| а б |  |
Рис. 8.5. Виброграмма колебаний:
Незатухающие колебания, вызванные постоянно действующей внешней силой, находящейся за пределами конструкции, называют автоколебаниями. Это колебания линий электропередач, вантовых мостов, высоких гибких мачт и других конструкций при постоянной скорости ветра.
Рис. 8.6. Колебания балки:
а – первой формы; б – второй; в – третьей; г – четвертой
Отношение значения какой-либо величины при динамической нагрузке к ее значению при статической нагрузке (рис. 8.7) называют динамическим коэффициентом:
Где 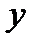

Рис.8.7. К определению динамического коэффициента
При действии вибрационной нагрузки наибольший амплитудный динамический коэффициент, определяемый без учета сопротивлений, вычисляется по формуле
 | (8.1.) |
Где 

Динамический коэффициент установившихся колебаний с учетом неупругих сопротивлений определяется по формуле [8.2]:
 | (8.2.) |
При 



Значения коэффициента 


При 

Например, для груза, подвешенного к пружине и под действием возмущающей силы перемещающегося вниз, возмущающая сила имеет наибольшее значение и тоже направлена вниз. При приближении к резонансу сдвиг фаз возрастает, а когда 
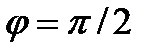



 Рис.8.8. Резонансные кривые при различных значениях Рис.8.8. Резонансные кривые при различных значениях  |  Рис.8.9. Сдвиг фазы в зависимости от затуханий и частоты возбуждения Рис.8.9. Сдвиг фазы в зависимости от затуханий и частоты возбуждения |
Пределом выносливости называют максимальное напряжение, при котором материал не разрушается при заданном числе циклов переменных нагрузок. Значительное влияние на предел выносливости оказывают минимальные и максимальные напряжения цикла (см. рис. 8.4). Отношение этих напряжений называют характеристикой цикла:
Среднее напряжение и амплитуда цикла определяются
При динамической нагрузке большой интенсивности, но малой продолжительности (взрыв, удар) наблюдается увеличение временного сопротивления материала. Происходит так называемое динамическое упрочнение.
Большое влияние на предел выносливости оказывает количество циклов повторно переменной нагрузки. Иногда продолжительно действующая периодическая нагрузка может создавать значительный динамический эффект. Однако при больших напряжениях разрушение может произойти и при малом числе циклов в результате малоцикловой усталости материала. Все эти обстоятельства необходимо учитывать при динамических расчетах строительных конструкций.
В некоторых случаях динамическая нагрузка может вызвать потерю общей или местной устойчивости конструкции, а для высоких гибких сооружений и призматических конструкций при воздействии потока ветра возможна аэродинамическая неустойчивость вследствие вихревого возбуждения, или галопирования.
Для обеспечения нормальных условий работы людей, технологического оборудования и измерительных приборов ограничивается амплитуда динамических перемещений: 

Сейсмическая нагрузка относится к числу особых и зависит от силы сейсмического воздействия, измеряемого в баллах, периода и формы свободных колебаний конструкции и ее массы. Колебания распространяются от эпицентра землетрясения во все стороны в виде продольных, поперечных и поверхностных сейсмических волн.
Динамический расчет зданий, расположенных в сейсмических районах, основан на упрощенных предпосылках норм. При расчете конструкции учитывают статическое действие сейсмических сил, распределенных в зависимости от массы сооружения. Расчетная сейсмическая нагрузка 

Где 








Колебания здания выражаются законом затухающей синусоиды при горизонтальном направлении сейсмических сил вдоль продольной или поперечной осей здания с точкой их приложения в уровнях междуэтажных перекрытий. Расчетная схема сооружения имеет вид консольного стержня на подвижном основании с произвольным расположением по его высоте масс и жесткостей (рис. 8.10). Для протяженных в плане зданий схему следует усовершенствовать. Если масса и жесткость здания по высоте изменяются незначительно, учитывают колебания только первого тона. Для гибких высотных сооружений учитываются колебания и высших тонов.
Колебания при землетрясениях носят хаотический нестационарный характер и трудно поддаются описанию четкими математическими зависимостями. Условно колебательный процесс рассматривается как случайный стационарный, как суммарное действие ряда гармонических колебаний. Представляют интерес не только перемещения и скорость, но главным образом сопровождающие их ускорения с отдельными пиковыми выбросами. Для записи сейсмометрических данных применяют различные измерительные приборы.
При динамических испытаниях, так же как и при статических, напряжения не поддаются непосредственному измерению, и их приходится определять косвенными методами: по деформациям, по амплитуде и форме колебаний, по ускорениям и перемещениям.
Рис.8.10. Расчетная схема сооружения при сейсмических воздействиях