Дискретная непрерывность что это

Дискретная непрерывность и разрывы (Австралия)

Если какая-то целочисленная величина в процессе меняется на каждом шаге не больше чем на 1 (в ту или другую сторону), то она обязательно проходит через все промежуточные значения между начальным и конечным. Такая величина называется дискретной, а прием – дискретной непрерывностью..

1. В футбольном матче первым забил «Спартак», а выиграло «Торпедо». Докажите, что в какой то момент счет был ничейный.

2. В ряд выложены 200 шаров, из них 100 черных и 100 красных, причем первый и последний шары – черные. Докажите, что можно убрать с правого края несколько шаров подряд так, чтобы красных и черных шаров осталось поровну.

Полезно раскрасить объекты в два цвета так, чтобы граница или разрыв отделяли цвета.

3. В последовательности целых чисел каждое число, начиная со второго, на 1 больше предыдущего или в 3 раза меньше предыдущего. Первое число равно 1, последнее равно 100. Докажите, что среди чисел есть и 77. ( Могут быть и числа больше 100)

4. В ряд лежат 100 яблок, соседние отличаются не более чем на 10 г. Докажите, что если выложить яблоки в ряд по возрастанию веса, то и тогда соседние будут отличаться не более чем на 10 г.

Если процесса нет, организуй сам. Подбери начало и конец процесса так, чтобы они были по разные стороны от нужного значения.

5. В ряд сидит 15 мальчиков и 15 девочек.
а) Докажите, что можно выбрать 10 школьников подряд, чтобы среди них мальчиков и девочек было поровну.
б) Всегда ли из них можно выбрать 20 школьников подряд, среди которых мальчиков и девочек поровну?

6. а) По кругу сидят 30 школьников, среди них мальчиков и девочек поровну. Докажите, что можно выбрать 20 школьников подряд, чтобы среди них мальчиков и девочек было поровну.
б) По кругу сидят 30 школьников, среди них мальчиков и девочек поровну. Докажите, что можно выбрать 18 школьников подряд, чтобы среди них мальчиков и девочек было поровну.

7. На клетчатой доске 100×100 стоит 3000 шашек. Докажите, что где бы они не стояли, доску можно разрезать по границам клеток на три части, в каждой из которых будет по 1000 шашек.

В некоторых процессах полезно начало и конец поменять местами. Тут помогает расположение на окружности.

8. На клетчатой рамке 100×100 толщиной в одну клетку стоит 150 шашек. Докажите, что рамку можно разрезать по границам клеток на две равные части с равным количеством шашек.

9. На клетчатой доске 100×100 стоит 1000 шашек. Докажите, доску можно разрезать по границам клеток на две равные части с равным количеством шашек.

Задачи посложнее сводятся к типовым с помощью приёма «засада на переправе»: показывается, что нужный результат достигается в момент прохода дискретной величины через определённое значение.

10. У Кости была кучка из 100 камешков. Каждым ходом он делил какую-то из кучек на две меньших, пока у него в итоге не оказалось 100 кучек по одному камешку. Докажите, что в какой-то момент в каких-то 30 кучках было в сумме ровно 60 камешков.

Московские сборы, 9 класс, А. Шаповалов www. ashap. info 7 апреля 2013 г.

Дискретная непрерывность. Домашнее задание (Австралия)

ДН1. В ряд стоят несколько солдат. Рост соседей отличается не более чем на 2,4 см.
а) В строю есть солдат ростом 152 см, и солдат ростом 198 см. Докажите, что есть солдат, чей рост отличается от 170 см не более, чем на 1,2 см.
б) Докажите, что если солдаты встанут по росту, то по-прежнему рост соседей будет отличаться не более, чем на 2,4 см.

ДН3. В бесконечной последовательности натуральных чисел каждое следующее число получается прибавлением к предыдущему одной из его ненулевых цифр. Докажите, что в этой последовательности найдется четное число.

ДН4. За круглым столом равномерно посажены 100 дедов, причем у любых двух соседей количество волос в бородах отличается не больше, чем на 100. Докажите, что найдется пара дедов, сидящих напротив друг друга, у которых количество волос в бородах также отличается не больше, чем на 100.

ДН5’. В строке шестизначных чисел первое число последнее 654321. Соседние числа отличаются на 1 или на 1000. Ни одно число не делится на 1000. Докажите, что хотя бы одно число делится на 13.

ДН6. В одном из 100 окопов, расположенных в ряд, спрятался робот-пехотинец. Автоматическая пушка может одним выстрелом накрыть любой окоп. В каждом промежутке между выстрелами робот (если уцелел) обязательно перебегает в соседний окоп (быть может, только что обстрелянный).
а) Известно, что вначале слева от робота – нечетное число пустых окопов. Сможет ли пушка наверняка накрыть робота?
б) Вначале робот может быть в любом из окопов. Сможет ли пушка наверняка накрыть робота?

ДН7. Дракон заточил рыцаря в темницу и выдал ему 100 различных монет, половина из которых – фальшивые (но какие именно – знает только дракон). Каждый день рыцарь раскладывает монеты на две кучки (не обязательно равные). Если в какой-то день в этих кучках окажется поровну настоящих монет, либо поровну фальшивых, то дракон отпустит рыцаря. Сможет ли рыцарь гарантированно освободиться не позже, чем на двадцать пятый день?

Источник

Что такое дискретность (дискретная математика, сигнал, величины, видеокарты, а так же дискретность в биологии)

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Знать все обо всем попросту невозможно. Человек на протяжении всей жизни стремится познать себя и окружающую его действительность.

Вот и сегодня мы продолжим свой познавательный процесс, поговорим о новом (для многих) термине – « дискретность», и о сферах, где он применяется.

Дискретность – это …

Наш мир непрерывен, мы живем в постоянно меняющемся времени и пространстве. Наша жизнь тоже непрерывна до своего конечного момента. Согласитесь, невозможно сейчас жить, через час не жить, а потом вновь возродиться.

В противопоставлении непрерывности существует дискретность. В переводе с «вечно живого» латинского языка «дискретность» (discretus) обозначает прерывность, разделенность.

Дискре́тность (от лат. discretus — разделённый, прерывистый) — свойство, противопоставляемое непрерывности, прерывистость. Синонимы к слову дискретный: корпускулярный, отдельный, прерывистый, раздельный и т. п.

Например, линия непрерывна (на определенном промежутке), пунктир – прерывистая линия. Поэтому пунктир можно назвать дискретной линией. Проиллюстрирую понятие дискретности:

Дискретность можно толковать следующим образом:

Далее проанализируем особенности применения термина в различных областях.

Дискретная математика

Если коротко и простыми словами, то дискретная математика (ДМ)– это наука, которые изучает математические объекты, принимающие отдельные (дискретные) значения.

ДМ условно подразделяется на пять направлений:

Дискретная величина

Дискретность какой-либо величины подразумевает, что ее значения можно пронумеровать, измерить и посчитать.

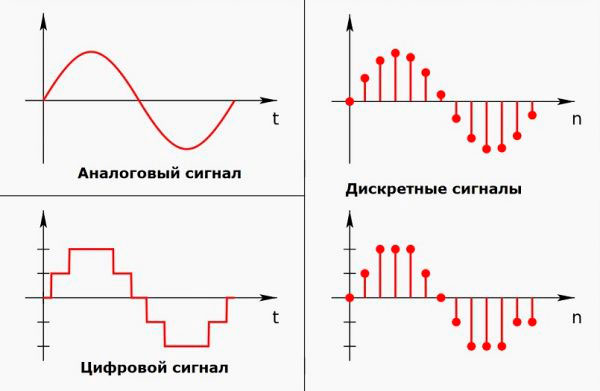
Такими величинами оперирует, например, экономика. Различные экономические показатели фиксируют и рассчитывают с определенной периодичностью (например, раз в месяц, квартал, полугодие и т.д.). Таким образом, изменение показателей происходит не непрерывно во времени, а как бы «скачками» через установленные интервалы времени.

Дискретность в информатике

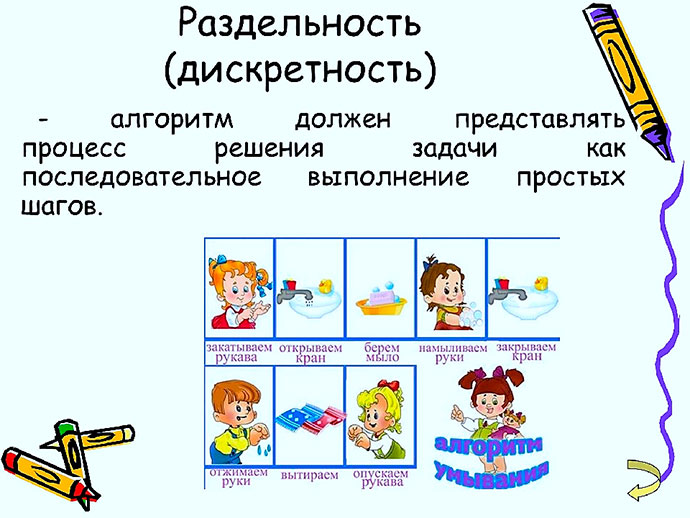
Программирование – это создание программ с использованием различных алгоритмов и языков программирования. Алгоритмы являются дискретными объектами, потому как представляют собой четкое последовательное выполнение ранее разработанных упрощенных шагов-действий (подпрограмм).

Только исполнение шага № 1 дает возможность выполнить шаг № 2 и т.д. Таким образом, этот процесс дискретен.

Как пример – алгоритм умывания (компьютерные программы создаются по тому же принципу):

Дискретная видеокарта

Видеокарта – один из важнейших элементов компьютера, отвечающий за визуализацию информации. Конструкция компа может быть оснащена либо интегрированной (встроенной) видеокартой, либо дискретной. Встроенная размещается в процессоре или на материнской плате, т.е. она неотделима от конкретного компьютера.

Дискретная видеокарта выполнена на отдельной плате, снабжена индивидуальным графическим процессором и памятью. Поэтому она более производительна, чем интегрированная.

Часто в компьютерах применяются видеокарты обоих видов, что позволяет пользователю при необходимости переключаться с одной на другую.

Дискретность в биологии

Все биологические объекты состоят из отдельных (дискретных) «кирпичиков», которые в совокупности образуют единый организм. Например, скелет человека состоит из костей, кости –из костной ткани, она, в свою очередь – из клеток.

Автор статьи: Елена Копейкина

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Благодарю за дискретное изложение материала

Источник

Дискретное и непрерывное

Чтобы понять суть противопоставления дискретного и непрерывного, сначала нужно определить, что означают эти понятия. Несмотря на то, что они имеют четкое математическое определение, они интуитивно понятны, и их легко продемонстрировать примерами из повседневной жизни. Противопоставление непрерывного и дискретного имеет некоторое сходство с противопоставлением потенциальной и актуальной бесконечности, поэтому неудивительно, что в обоих случаях дискуссия имеет больше философский смысл.

Ключевой вопрос дискуссии: дискретен или непрерывен наш мир? Этот вопрос очень тесно связан с нашими ощущениями и, как следствие, лежит в плоскости теории познания. В начале XX века физики и математики, будучи далеки от философских размышлений и психологических интерпретаций, без колебаний сделали свой выбор в пользу концепции дискретного мира с появлением квантовой механики и так называемой дискретной математики.

Толковый словарь русского языка дает слову «дискретный» такое определение: «прерывистый, дробный, состоящий из отдельных частей». Лучше всего понять смысл дискретности можно через ее противопоставление непрерывности. Например, время течет непрерывно с 9 утра до 9 вечера. Но если мы посмотрим на расписание поездов, которые отправляются с 9 утра до 9 вечера, то увидим дискретное множество значений. Если один поезд отправляется в 10 утра, а следующий — в 11, то между этими двумя значениями, 10 и 11, нет никакого другого, поэтому эти значения называют дискретными. Напротив, течение времени между 10 и 11 часами непрерывно, и время может равняться, например, 10 часам 25 минутам и 0,34628761720041244474 секунды. Если мы составим список европейских столиц и укажем для каждой из них число жителей, то получим дискретное множество значений. Напротив, уровень воды в водохранилище изменяется непрерывно между некими максимальным и минимальным значениями. Также никому не придет в голову сказать, что объем воды в обычном кувшине вместимостью, например, два литра, может принимать только дискретные значения, например только литр, пол-литра или 257 кубических сантиметров. Скорость автомобиля также изменяется непрерывно, что показывает стрелка спидометра, которая движется плавно, а не скачкообразно. Показания счетчика пробега, напротив, являются дискретными.

Как мы уже говорили, концепции дискретности и непрерывности являются интуитивно понятными и поэтому кажутся простыми. Тем не менее, вокруг них на протяжении многих лет кипят жаркие споры, и вопрос нельзя считать закрытым. Отчасти это происходит потому, что, как мы увидим позднее, интуиция не всегда хороший советчик. Иногда одно и то же явление кажется непрерывным или дискретным в зависимости от выбранного масштаба. Как бы то ни было, ответ на этот вопрос влияет на наше восприятие мира, поэтому интересует не только математиков, но и философов. Эти две точки зрения очень тесно связаны между собой. Французский математик Жан-Шарль де Борда (1733-1799) как-то сказал: «Без математики нельзя глубоко проникнуть в суть философии, без философии нельзя глубоко проникнуть в суть математики, а без того и другого нельзя понять суть чего бы то ни было».

Источник

Дискретная непрерывность что это

3. На базе диалектической логики возможен синтез этих подходов, и он характерен для современной науки. Но об этом – ниже.

Гипотеза о Д. времени занимает важное место в атомистике древних. Об этом рассказывает Аристотель. По-видимому, время у них складывается из ничтожных по длительности и больше неделимых мгновений. Вместе они образуют моменты единого для всего мира «настоящего времени» или «теперь». События, происшедшие в одно и то же мгновение, – одновременны. Фактически, это была первая версия т.н. «абсолютного времени». Изначально, в основе этого атомизма лежала идея о тождестве строения макро- и микрокосмоса: природа, будучи единой, должна быть устроена и в малейшей своей части так же, как и в величайшей. Эта идея в ХХ веке воплотилась сначала в планетарной модели атома Э.Резерфорда (1871-1937). Она стала основой и системно-структурного фундаментализма ХХ века (как у А.А.Богданова в его тектологии и Л.фон Берталанфи и др. в общей теории систем, в органицизме). Однако научное открытие атомов вещества произошло раньше всего в химии.

3) Химический атомизм, опираясь на взгляды Ньютона, создал впервые в Англии Дж.Дальтон (1766-1844). Он ввел представление об атомном весе, специфическом для каждого сорта атомов вещества. Атом в химии – самая маленькая порция вещества определенного вида. Появилось представление о молекулах как сочетании атомов, образующих все многообразие вещества в природе. Единицей атомного веса стал атом водорода. Впоследствии эти результаты привели русского химика Д.И.Менделеева (1834-1907) к созданию знаменитой химической периодической «системы Менделеева», обладавшей большими эвристическими возможностями для открытия новых и новых элементов. В XIX веке усилиями А.Купера и Ф.Кекуле была развита идея валентности, объяснение которой, как и химизма вообще, осуществила уже физика в атомной теории Н.Бора (1885-1962). Между тем, происходит познание новых видов движений и соответствующих им законов. Мы сегодня уже хотим узнать верхние и нижние границы химизма (например, есть ли т.н. “остров стабильности” в районе 120 номера таблицы Менделеева). Сейчас возникли вопросы о влиянии на наш мир темной материи и движения, роли нейтрино в рамках этой материи и др. вопросы.

По определению, Н. – неразрывная связь в бытии или переход в его становлении. Здесь действует закон, установленный Г.Лейбницем: «природа не делает скачков», ибо в ней все процессы сплошь состоят из скачков, и что в ней нет никаких пробелов и все связано благодаря переходам (см.: Непрерывность // Краткая философская …, с. 299-300). Вряд ли можно считать, что квантовая теория, где квант – атом энергии, оправдывает абсолютность квантования для всего микромира: каждый кантовый скачок в состояния электронов в атоме все-таки не происходит с бесконечно большой скоростью. Это вроде бы запрещено принципами релятивистской физики, кроме того, мы не знаем, что в это же время происходит с темной энергией и в её «среде».

Источник

Дискретная непрерывность что это

НЕПРЕРЫВНОСТЬ И ПРЕРЫВНОСТЬ

НЕПРЕРЫВНОСТЬ И ПРЕРЫВНОСТЬ – категории, характеризующие бытие и мышление; прерывность (дискретность) описывает определенную структурность объекта, его «зернистость», его внутреннюю «сложность»; непрерывность выражает целостный характер объекта, взаимосвязь и однородность его частей (элементов) и состояний. В силу этого категории непрерывности и прерывности являются взаимодополняющими при любом исчерпывающем описании объекта. Важную роль категории непрерывности и прерывности играют также при описании развития, где они превращаются соответственно в скачок и преемственность.

В силу своей философской фундаментальности категории непрерывности и прерывности подробно обсуждаются уже в греческой античности. Факт движения связывает воедино проблемы непрерывности и прерывности пространства, времени и самого движения. В 5 в. до н.э. Зенон Элейский формулирует основные апории, связанные как с дискретной, так и с непрерывной моделями движения. Зенон показал, что континуум не может состоять из бесконечно малых неделимых (из точек), т.к. тогда величина бы складывалась из невеличин, из «нулей», что непонятно, ни из конечных, имеющих величину неделимых, т.к. в этом случае, поскольку неделимых должно быть бесконечное множество (между любыми двумя точками найдется точка), это бесконечное множество конечных величин давало бы бесконечную величину. Проблема структуры континуума представляет собой тот проблемный узел, в котором неразрывно связаны категории непрерывности и прерывности. Причем то или иное понимание континуума в античности обычно истолковывается онтологически и соотносится с космологией.

Античные атомисты (Демокрит, Левкипп, Лукреций и др.) стремятся мыслить всю сферу сущего как своеобразную смесь дискретных элементов (атомов). Но довольно быстро происходит разделение точек зрения физических атомистов, мыслящих атомы неделимыми конечными элементами, и математических атомистов, для которых неделимые не имеют величины (точки). Последний подход успешно использует, в частности, Архимед для нахождения площадей и кубатур тел, ограниченных кривыми и неплоскими поверхностями. Абстрактно математический и физикалистский подходы еще не слишком рельефно разделены в античной мысли. Так, вопрос о природе треугольника, из которых в «Тимее» Платона складываются многогранники элементов, остается дискуссионным (проблема в том, что здесь из плоскостей складываются трехмерные элементы, т.е., вероятно, имеет место математический атомизм). Для Аристотеля непрерывное не может состоять из неделимых частей. Аристотель различает следующее по порядку, соприкасающееся и непрерывное. Каждое следующее в этом ряду оказывается спецификацией предыдущего. Существует следующее по порядку, но не соприкасающееся, напр. ряд натуральных чисел; соприкасающееся, но не непрерывное, напр. воздух над поверхностью воды. Для непрерывности необходимо, чтобы границы соприкасающихся совпадали. Для Аристотеля «все непрерывное делимо на части, всегда делимые» (Физика VI, 231b 15–17).

Еще острее вопрос о природе континуума обсуждается в средневековой схоластике. Рассматривая его в онтологической плоскости, сторонники и противники континуальной космологии относят другую возможность истолкования в сферу субъективного, только мыслимого (или чувственного). Так, Генрих Гентский утверждал, что существует собственно лишь континуум, а все дискретное, и прежде всего число, получается «отрицанием», через проведение границ в континууме. Николай из Отрекура, наоборот, считал, что хотя чувственно данный континуум и делим до бесконечности, в действительности же континуум состоит из бесконечного числа неделимых частей. Укреплению аристотелевского подхода к континууму служили дискуссии средневековых номиналистов (У. Оккам, Григорий из Римини, Ж.Буридан и др.). «Реалисты» понимали точку как онтологическую реальность, лежащую в основе всего сущего (Роберт Гроссетест).

Традицию физического атомизма – «линию Демокрита» – подхватывает в 16 в. Дж.Бруно. Атомистика же Галилея в 17 в. носит явно математический характер («линия Архимеда»). Тела у Галилея состоят из бесконечно малых атомов и бесконечно малых промежутков между ними, линии строятся из точек, поверхности – из линий и т.д. В философии зрелого Лейбница была дана оригинальная интерпретация соотношения непрерывности и прерывности. Лейбниц разводит непрерывность и прерывность по разным онтологическим сферам. Действительное бытие – дискретно и состоит из неделимых метафизических субстанций – монад. Мир монад не дан непосредственному чувственному восприятию и открывается только размышлением. Непрерывное же является основной характеристикой лишь феноменального образа Универсума, т.к. он наличествует в представлении монады. В действительности части – «единицы бытия», монады – предшествуют целому. В представлениях же, данных в модусе пространства и времени, целое предшествует частям, на которые это целое можно бесконечно делить. Мир непрерывного не есть мир действительного бытия, а мир лишь возможных отношений. Непрерывны пространство, время и движение. Более того, принцип непрерывности является одним из фундаментальных начал сущего. Лейбниц формулирует принцип непрерывности следующим образом: «Когда случаи (или данные) непрерывно приближаются друг к другу так, что наконец один переходит в другой, то необходимо, чтобы и в соответствующих следствиях или выводах (или в искомых) происходило то же самое» (Лейбниц Г.В. Соч. в 4 т., т. 1. М., 1982, с. 203– 204). Лейбниц показывает применение этого принципа в математике, физике, теоретической биологии, психологии. Проблему структуры континуума Лейбниц уподоблял проблеме свободы воли («два лабиринта»). При обсуждении обоих мышление сталкивается с бесконечностью: в бесконечность уходит процесс нахождения общей меры для несоизмеримых отрезков (по алгоритму Евклида) и в бесконечность же простирается цепь детерминации лишь по видимости случайных (но на самом деле подчиняющихся совершенной божественной воле) истин факта. Лейбницевской онтологизации границы между непрерывностью и прерывностью не суждено было стать господствующей точкой зрения. Уже X.Вольф и его ученики опять начинают дискуссии о построении континуума из точек. Кант, полностью поддерживая лейбницевский тезис о феноменальности пространства и времени, строит тем не менее континуалистскую динамическую теорию материи. Последняя существенно повлияла на Шеллинга и Гегеля, которые также выдвигали ее против атомистических представлений.

В русской философии на рубеже 19–20 вв. возникает противостояние «культу непрерывности», связанное с именем математика и философа Н.В.Бугаева. Бугаев разработал систему миросозерцания, основанную на принципе разрывности как фундаментальном принципе мироздания (аритмология). В математике этому принципу соответствует теория разрывных функций, в философии – особый тип монадологии, развитый Бугаевым. Аритмологическое мировоззрение отрицает мир как сплошность, зависящую только от самой себя и постижимую в понятиях непрерывности и детерминизма. В мире есть свобода, откровение, творчество, разрывы непрерывности – как раз те «зияния», которые отвергает принцип непрерывности Лейбница. В социологии аритмология в противовес «аналитическому мировоззрению», видящему во всем только эволюцию, подчеркивает катастрофические аспекты исторического процесса: революции, перевороты в личной и общественной жизни. Вслед за Бугаевым подобные взгляды развивал П.А.Флоренский.

НЕПРЕРЫВНОСТЬ И ПРЕРЫВНОСТЬ В МАТЕМАТИКЕ. В силу большей, чем в современности, зависимости от онтологии математика античности не слишком отделяет свою точку зрения на непрерывность и прерывность от физики и математики. Дискретное – как число – и непрерывное – «величина» (т.е. континуальная пространственная величина) – мыслятся раздельно и несводимы одна к другой. Числом занимается арифметика, величинами – геометрия, и познавательный статус первой, согласно платоновско-пифагорейской традиции, выше, чем второй. Средневековье углубляет дискуссию о соотношении непрерывности и прерывности, вводя новые важные логические дистинкции (напр., категории синкатегорематической и категоруматической бесконечности, тесно связанные с проблемой деления континуума). С изобретением в 17 в. дифференциального и интегрального исчислений проблема арифметизации континуума становится все более насущной. Однако положительного решения ее пришлось ждать вплоть до 2-й пол. 19 в., когда появились арифметические конструкции действительного числа К.Вейерштрасса, Ш.Мере, Р.Дедекинда и Г.Кантора. Все эти конструкции существенно использовали актуальную бесконечность. Кантор попытался в рамках созданной им теории множеств оценить мощность арифметических моделей континуума. 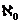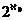Мощность множества натуральных чисел («счетного множества») обозначалась им через («алеф» – первая буква древнееврейского алфавита). Тогда, согласно теоремам теории множеств, мощность арифметического континуума будет .

Кантор выдвинул предположение («континуум – гипотеза»), что мощность континуума является наименьшей из следующих за 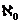мощностей, т.е.

Доказательство континуум-гипотезы означало бы, что континуум в некотором обобщенном смысле может быть «исчислен» или «сложен из точек». Эту гипотезу, однако, не удалось доказать ни Кантору, ни его последователям. В 1963 П.Коэн показал, что континуум-гипотеза не может быть ни доказана, ни опровергнута в теории множеств, опирающейся на систему аксиом Цермело–Френкеля.

В более же широком смысле понятие непрерывности определяется в сегодняшней математике формально, в рамках топологии. Через аксиоматически вводимое понятие близости точек («окрестность точки») можно определить понятия предельного перехода и непрерывности функций. Т.о. возникают самые различные топологические пространства, моделирующие всевозможные типы непрерывности (включая и дискретную топологию). В то же время существует целый ряд нестандартных моделей континуума: конструкции Э.Л.Брауэра и Г.Вейля в рамках интуиционистской математики, специальные модели в альтернативных (неканторовских) теориях множеств, в «нестандартном анализе» А.Робинсона. Взаимосоотнесенность свойств непрерывности и прерывности ярко проявилась в 20 в. в квантовой физике. Классические представления о движении частицы и волны пришлось заменить представлением о сосуществовании корпускулярных и волновых свойств в едином физическом объекте. Наряду с классическими представлениями о пространственно-временном континууме предпринимаются попытки квантования пространства и времени. В 1970-х гг. в связи с прогрессом компьютерной техники началась революция в методах обработки дискретной («цифровой») информации. Фантастически возрастающее быстродействие компьютера позволяет внедрять его в качестве узлового звена в сложные процессы современного управления производством, военными системами, образованием и т.д. Вместе с этим встают сложнейшие философские вопросы о границах человеческой ответственности, о допустимых пределах автоматизации, о природе мышления и человеческой сущности вообще. «Взрывное» развитие сегодняшней компьютерной техники заставляет говорить о начале новой «информационной цивилизации» и вновь ставит вопросы о соотношении дискретного и континуального в человеке и в природе вообще.

1. Дедекинд Р. Непрерывность и иррациональные числа. Одесса, 1923;

2. Вейль Г. Математическое мышление. M., 1989;

3. Кантор Г. Труды по теории множеств. М., 1985;

4. Гейтинг А. Интуиционизм. Введение. М., 1965;

5. Зубов В.П. Развитие атомистических представлений до начала XIX века. М., 1965;

6. Коэн П. Теория множеств и континуум-гипотеза. М., 1973;

7. Катасонов В.Н. Метафизическая математика XVII века. М., 1993;

8. Breidert W. Das aristotelische Kontinuum in der Scholastik. Münster, 1970;

9. Duhem P. Leonard de Vinci et les deux infinis. – Etudes sur Leonard de Vinci. P., 1909.

Источник