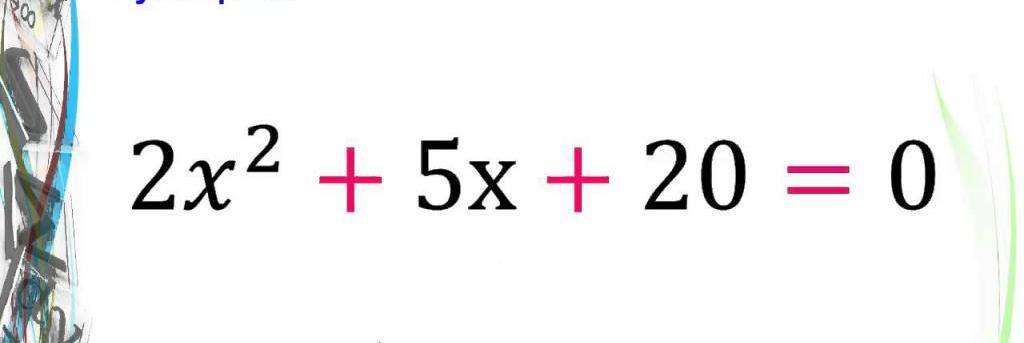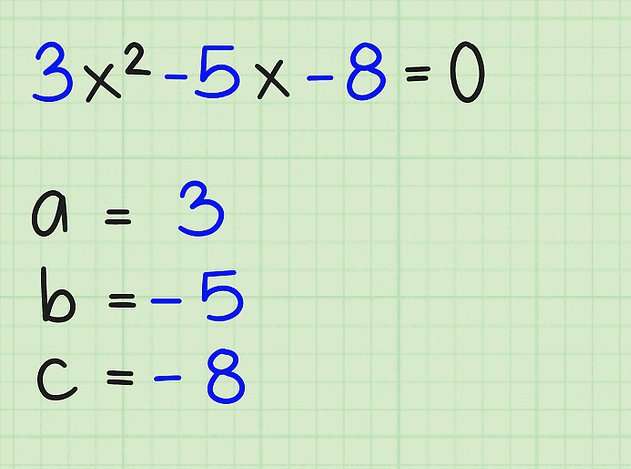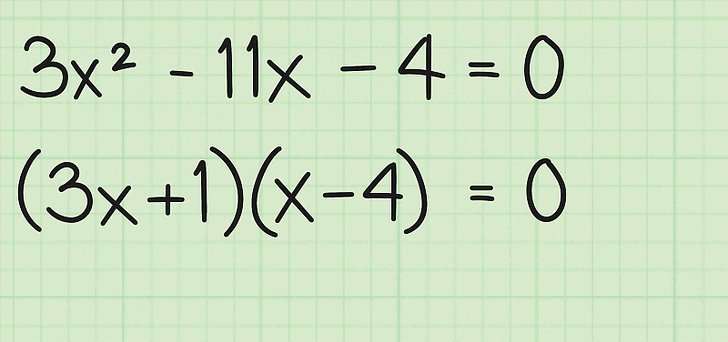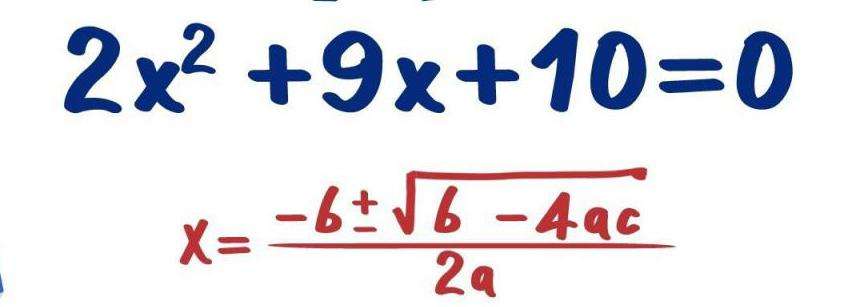Дискриминант или виета что лучше

Квадратное уравнение. Дискриминант. Теорема Виета.

теория по математике 📈 уравнения

Уравнение вида ax 2 +bx+c=0, где a,b,c – любые числа, причем a≠0, называют квадратным уравнением. Числа a,b,c принято называть коэффициентами, при этом a – первый коэффициент, b – второй коэффициент, c – свободный член.

Квадратное уравнение может иметь не более двух корней. Решить такое уравнение – это значит найти все его корни или доказать, что их нет.

Дискриминант

Количество корней квадратного уравнения зависит от такого элемента, как дискриминант (обозначают его буквой D).

Нахождение корней квадратного уравнения

Дискриминант – это такой математический инструмент, который позволяет нам определять количество корней. Он выражается определенной формулой:

D=b 2 –4ac

Пример №1. Решить уравнение х 2 –2х–3=0. Определяем коэффициенты: а=1, b=–2, c=–3. Находим дискриминант: D=b 2 –4ac=(–2) 2 –41(–3)=4+12=16. Видим, что дискриминант положительный, значит, уравнение имеет два различных корня, находим их:

Пример №2. Решить уравнение 5х 2 +2х+1=0. Определяем коэффициенты: а=5, b=2, c=1. D=b 2 –4ac=2 2 –4=4–20=–16, D 2 –6х+9=0. Определяем коэффициенты: а=1, b=–6, c=9.

D=b 2 –4ac=(–6) 2 –4=36–36=0, D=0, 1 корень

Теорема Виета

Среди квадратных уравнений встречаются такие, у которых первый коэффициент равен 1 (обратим внимание на пример 1 и 3), такие уравнения называются приведенными.

Приведенные квадратные уравнения можно решать не только с помощью дискриминанта, но и с помощью теоремы Виета.

Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком; произведение корней равно третьему коэффициенту.

Корни с помощью данной теоремы находятся устно способом подбора. Рассмотрим это на примерах.

Пример №4. Решить уравнение х 2 –10х+21=0. Выпишем коэффициенты: а=1, b=–10, c=21. Применим теорему Виета:

Начинаем с произведения корней, которое является положительным числом, значит оба корня либо отрицательные, либо положительные. Предполагаем, что это могут быть либо 3 и 7, либо противоположные им числа. Теперь смотрим на сумму, она является положительным числом, поэтому нам подходит пара чисел 3 и 7. Проверяем: 3+7=10, 37=21. Значит, корнями данного уравнения являются числа 3 и 7.

Пример №5. Решить уравнение: х 2 +5х+4=0. Выпишем коэффициенты: а=1, b=5, c=4. По теореме Виета:

Видим, что произведение корней равно 4, значит оба корня либо отрицательные, либо положительные. Видим, что сумма отрицательная, значит, будем брать два отрицательных числа, нам подходят –1 и –4. Проверим:

Источник

Методы решения квадратных уравнений. Формула Виета для квадратного уравнения

Квадратные уравнения часто появляются в ряде задач по математике и физике, поэтому уметь их решать должен каждый школьник. В этой статье подробно рассматриваются основные методы решения уравнений квадратных, а также приводятся примеры их использования.

Какое уравнение называется квадратным

Вам будет интересно: Химические цепочки превращений: примеры и способы решения

Уравнение, в котором a=1, называют приведенным, то есть оно вид имеет: x2 + с/a + (b/a)*x =0.

Какие методы решения уравнений квадратных существуют

В общем случае существует 4 метода решения. Ниже перечисляются их названия:

Вам будет интересно: Каково значение слова «транспарентность»?

Как понятно из приведенного списка, первые три метода являются алгебраическими, поэтому они используются чаще, чем последний, который предполагает построение графика функции.

Существует еще один способ решения по теореме Виета уравнений квадратных. Его можно было бы включить 5-м в список выше, однако, это не сделано, поскольку теорема Виета является простым следствием 3-го метода.

Далее в статье рассмотрим подробнее названные способы решения, а также приведем примеры их использования для нахождения корней конкретных уравнений.

Метод №1. Разложение на множители

Для этого метода в математике квадратных уравнений существует красивое название: факторизация. Суть этого способа заключается в следующем: необходимо квадратное уравнение представить в виде произведения двух членов (выражений), которое должно равняться нулю. После такого представления можно воспользоваться свойством произведения, которое будет равно нулю только тогда, когда один или несколько (все) его членов являются нулевыми.

Теперь рассмотрим последовательность конкретных действий, которые нужно выполнить, чтобы найти корни уравнения:

Вам будет интересно: Коммуникативная методика обучения английскому языку: главные принципы, учебники, результаты, отзывы

Как видно, алгоритм факторизации является достаточно простым, тем не менее, у большинства школьников возникают трудности во время реализации 2-го пункта, поэтому поясним его подробнее.

Чтобы догадаться, какие 2-а линейных выражения при умножении их друг на друга дадут искомое квадратное уравнение, необходимо запомнить два простых правила:

После того, как подобраны все числа множителей, следует выполнить их перемножение, и если они дают искомое уравнение, тогда переходить к пункту 3 в изложенном выше алгоритме, в противном случае следует изменить множители, но делать это нужно так, чтобы приведенные правила всегда выполнялись.

Пример решения методом факторизации

Покажем наглядно, как алгоритм решения уравнения квадратного составить и найти неизвестные корни. Пусть дано произвольное выражение, например, 2*x-5+5*x2-2*x2 = x2+2+x2+1. Перейдем к его решению, соблюдая последовательность пунктов от 1-го до 3-х, которые изложены в предыдущем пункте статьи.

Пункт 1. Перенесем все члены в левую часть и выстроим их в классической последовательности для квадратного уравнения. Имеем следующее равенство: 2*x+(-8)+x2=0.

Пункт 3. Приравниваем каждый множитель нулю, получаем: x=-4 и x=2.

Если возникают какие-либо сомнения в полученном результате, то рекомендуется выполнить проверку, подставляя найденные корни в исходное уравнение. В данном случае имеем: 2*2+22-8=0 и 2*(-4)+(-4)2-8=0. Корни найдены правильно.

Метод №2. Дополнение до полного квадрата

В алгебре уравнений квадратных метод множителей не всегда может использоваться, поскольку в случае дробных значений коэффициентов квадратного уравнения возникают сложности в реализации пункта 2 алгоритма.

Метод полного квадрата, в свою очередь, является универсальным и может применяться для квадратных уравнений любого типа. Суть его заключается в выполнении следующих операций:

Описанный алгоритм может на первый взгляд быть воспринят, как достаточно сложный, однако, на практике его реализовать проще, чем метод факторизации.

Пример решения с помощью дополнения до полного квадрата

Пункт 4. Вычисляем квадратный корень с положительным и отрицательным знаками и находим корни: x = 3/5±√59/5 = (3±√59)/5. Два найденных корня имеют значения: x1 = (√59+3)/5 и x1 = (3-√59)/5.

Таким образом, мы показали, что найденные корни уравнения являются истинными.

Метод №3. Применение известной формулы

Этот метод решения уравнений квадратных является, пожалуй, самым простым, поскольку он заключается в подставлении коэффициентов в известную формулу. Для его использования не нужно задумываться о составлении алгоритмов решения, достаточно запомнить только одну формулу. Она приведена на рисунке выше.

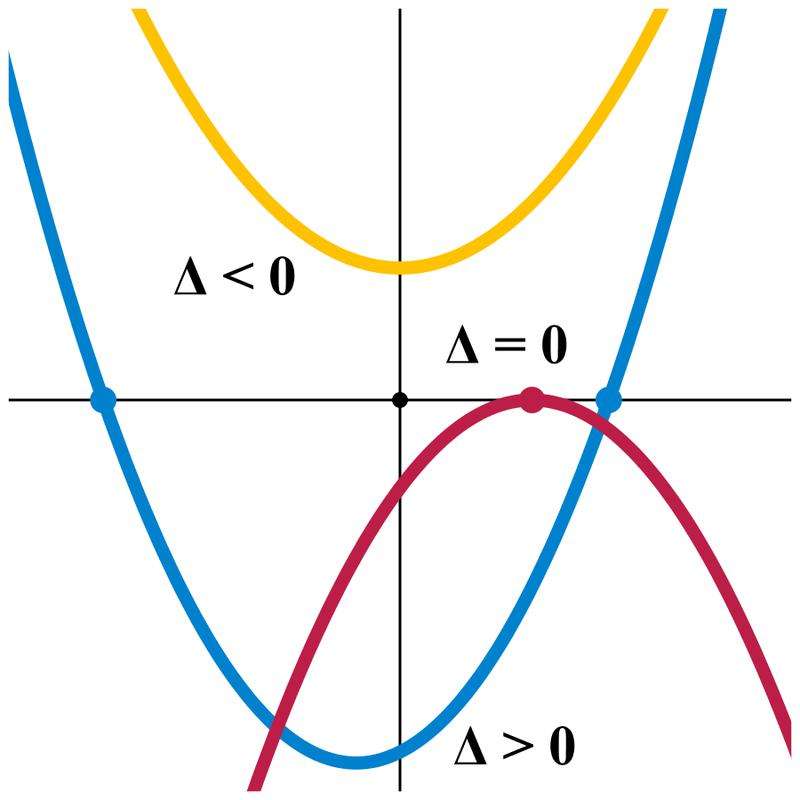
В этой формуле подкоренное выражение (b2-4*a*c) называется дискриминантом (D). От его значения зависит то, какие корни получатся. Возможны 3-и случая:

Теорема Виета

Как выше было отмечено, эта теорема является следствием метода №3, который основан на применении формулы с дискриминантом. Суть теоремы Виета заключается в том, что она позволяет связать в равенство коэффициенты уравнения и его корни. Получим соответствующие равенства.

Таким образом, для решения уравнений квадратных по теореме Виета можно использовать полученных два равенства. Если все три коэффициента уравнения известны, тогда корни можно найти путем решения соответствующей системы из этих двух уравнений.

Пример использования теоремы Виета

Обратное применение Виета теоремы, то есть вычисление корней по известному виду уравнения, позволяет для небольших целых чисел a, b и c быстро (интуитивно) находить решения.

Источник

Теорема Виета для квадратного уравнения

Основные понятия

Квадратное уравнение — это ax 2 + bx + c = 0, где a — первый коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Существует три вида квадратных уравнений:

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Формула для его поиска записывается так: D = b 2 − 4ac. Его свойства:

В математике теоремой принято называть утверждение, у которого ранее было сформулировано доказательство.

Формула Виета

Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:

Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:

Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0.

Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:

Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:

Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
2 + 4x + 3 = 0″ height=»215″ src=»https://lh5.googleusercontent.com/E_X403ETh_88EANRWdQN03KRT8yxP2HO4HoCrxj__c8G0DqmNJ1KDRqtLH5Z1p7DtHm-rNMDB2tEs41D7RHpEV5mojDTMMRPuIkcW33jVNDoOe0ylzXdHATLSGzW4NakMkH2zkLE» width=»393″>

Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
2 + 4x + 3 = 0″ height=»52″ src=»https://lh5.googleusercontent.com/VzGPXO9B0ZYrr9v0DpJfXwuzeZtjYnDxE_ma76PUC8o7jVWwa8kZjTJhq2Lof0TiJXAp_ny3yRwI_OyRzeucv9xUZ63yoozGPP4xd4OxvElVT7Pt-d6xL5w17e_mQNs5qZJQiwfG» width=»125″>

Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
2 + 4x + 3 = 0″ height=»52″ src=»https://lh4.googleusercontent.com/Cq-LCFmY3YGNSan1VF3l3CqIeojoJYAvGAiTBWnzyoZu_xJFrF5NfQ3xCe59apJklw6uYbmQ4lAkBTeC-TJmEGicN3rgGtsezhuqdNiOWjZT39NziOB5uOmQr3cr9-5fNnepdZDo» width=»112″>

Результат проделанных вычислений в том, что мы убедились в справедливости выражения:

Обучение на курсах по математике помогает быстрее разобраться в новых темах и подтянуть оценки в школе.

Доказательство теоремы Виета

Дано квадратное уравнение x 2 + bx + c = 0. Если его дискриминант больше нуля, то оно имеет два корня, сумма которых равна второму коэффициенту с противоположным знаком, а произведение корней равно свободному члену:

Докажем, что следующие равенства верны

Чтобы найти сумму корней x₁ и x₂ подставим вместо них то, что соответствует им из правой части формул корней. Напомним, что в данном квадратном уравнении x 2 + bx + c = 0 старший коэффициент равен единице. Значит после подстановки знаменатель будет равен 2.

Мы доказали: x₁ + x₂ = −b.

Далее произведем аналогичные действия, чтобы доказать о равенстве x₁ * x₂ свободному члену c.

Мы доказали: x₁ * x₂ = c.

Значит сумма корней приведённого квадратного уравнения x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком (x₁ + x₂ = −b), а произведение корней равно свободному члену (x₁ * x₂= c). Теорема доказана.

Обратная теорема Виета

Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Она формулируется так:

Обратная теорема Виета

Если числа x₁ и x₂ таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа являются корнями x 2 + bx + c = 0.

Обратные теоремы зачастую сформулированы так, что их утверждением является заключение первой теоремы. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это является утверждением.

Докажем теорему, обратную теореме Виета

Корни x₁ и x₂ обозначим как m и n. Тогда утверждение будет звучать следующим образом: если сумма чисел m и n равна второму коэффициенту x 2 + bx + c = 0, взятому с противоположным знаком, а произведение равно свободному члену, то числа m и n являются корнями x 2 + bx + c = 0.

Зафиксируем, что сумма m и n равна −b, а произведение равно c.

Чтобы доказать, что числа m и n являются корнями уравнения, нужно поочередно подставить буквы m и n вместо x, затем выполнить возможные тождественные преобразования. Если в результате преобразований левая часть станет равна нулю, то это будет означать, что числа m и n являются корнями x 2 + bx + c = 0.

При x = m получается верное равенство. Значит число m является искомым корнем.

Мы доказали: числа m и n являются корнями уравнения x 2 + bx + c = 0.

Примеры

Для закрепления знаний рассмотрим примеры решения уравнений по теореме, обратной теореме Виета.

Дано: x 2 − 6x + 8 = 0.

Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.
2 − 6x + 8 = 0″ height=»59″ src=»https://lh6.googleusercontent.com/tFokx3SM93Hwlr7ZM9BqX1xiHKv_2dUIB9MoNa8RAwSTmQKXdCcqcFXxTZmxNGw7bOVek-RzRXqBkoCqnYMiqIYVwKhfnHeU-7mA03feEqJTlyKB7e-OsTTKgPaOlddfiaTGszcv» width=»99″>

Имея эти два равенства можно подобрать подходящие корни, которые будут удовлетворять как равенству обоим равенствам системы.

Подбор корней удобнее выполнять с помощью их произведения. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.

Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. Значения 4 и 2 подходят обоим равенствам:

Значит числа 4 и 2 являются корнями уравнения x 2 − 6x + 8 = 0.
2 − 6x + 8 = 0″ height=»57″ src=»https://lh3.googleusercontent.com/rohB7Bvd-elMhTxEUuOhKqLJjqLAvo9VlJxZvOnMeDAHARfKT-SYOWb1WXTTWEN2h0oKbLl6wH7lc0IWL_vH3Si2AJGAGXVn8TPFDT_J1Wu2WeoQ-WP1qgXjCnZ99tWUkK2BOvF2″ width=»64″>

Неприведенное квадратное уравнение

Теорема Виета выполняется только тогда, когда квадратное уравнение является приведённым, то есть его первый коэффициент равен единице:

ax 2 + bx + c = 0, где а = 1.

Источник

Об отдельных случаях вычисления дискриминанта

Сложно встретить старшеклассника, НЕ умеющего находить корни квадратного уравнения через дискриминант.

Но, к сожалению, в отдельных случаях, получая громоздкий дискриминант, многие начинают паниковать (без калькулятора).

А на ЕГЭ по математике, например, в задачах №11, вам вполне может встретиться причудливый дискриминант.

Нет безвыходных ситуаций!

На чем можно сэкономить силы при вычислении дискриминанта

Прежде чем разбирать примеры, вспомним все же формулу дикриминанта для вычисления корней квадратного уравнения

Тогда корни уравнения находим по формуле

Надеюсь, вы помните, что удобно искать корни уравнения через дискриминант в случае, если имеем дело с полным квадратным уравнением ( и – ненулевые).

I. Используем формулу «разность квадратов» + показать

Допустим, нам нужно решить уравнение

Ясно, что дискриминант следующий:

Не спешим возводить 53 в квадрат! Замечаем, что , поэтому

Корни данного уравнения, думаю, теперь каждый из вас найдет без труда…

II. Используем прием вынесения общего множителя за скобки + показать

Допустим, нам нужно решить уравнение (кстати, оно взято из реальной текстовой задачи из открытого банка заданий ЕГЭ по математике).

Ясно, что дискриминант следующий:

Нет, мы не пойдем напролом!

Замечаем, что , а .

Мы можем вынести за скобку общий множитель

Корни найти – уже не проблема…

III. Формула сокращенного дискриимнанта + показать

Допустим, нам нужно решить уравнение

Вы знаете, что такое ? [spoiler]

Его очень удобно применять в случае четности второго коэффициента (при ).

Вот формулы дискриминанта и корней в этом случае:

для уравнения , где – четное

Тогда корни следующие: , то есть или

Хоть на чуть-чуть, но упростили вычисления. Считаете, что неоправданно, – лишней формулой забивать голову… Выбор за вами.

IV. Вместо дискриминанта – т. Виета + показать

Допустим, нам нужно решить уравнение

Вспоминаем теорему Виета:

Для приведенного квадратного уравнения (т.е. такого, коэффициент при в котором равен единице) сумма корней равна коэффициенту , взятому с обратным знаком, а произведение корней равно свободному члену , то есть ,

Так вот, очевидно, на роль корней уравнения претендуют числа и , так как и

Источник