Дислокации характеризуются тем что
Дислокации и их влияние на структуру материала
Дислокациями называют линейные дефекты кристаллов, возникающие в процессе роста или пластической деформации. Различают краевые и винтовые дислокации, нарушающие правильное чередование атомных плоскостей.
Причиной краевой дислокации является отрыв одной из плоскостей внутри кристалла. Образование винтовой дислокации связано, в основном, с условиями роста кристалла, состоящего из одной атомной плоскости, изгибающейся по винтовой поверхности.
Дислокации в кристалле могут возникать при его росте и в том случае, когда растущие навстречу друг другу блоки или зерна повернуты один относительно другого. При срастании таких блоков образуются избыточные атомные плоскости, которые определяют текстуру реальных кристаллов.
Причиной образования дислокаций в кристалле могут быть также скопления точечных дефектов, в частности, вакансий.
В процессе пластической деформации происходит не одновременный сдвиг всех атомов данной плоскости, а последовательное перемещение связей между атомами, лежащими по обе стороны плоскости скольжения. Такое перераспределение связей предопределяет движение дислокаций от одной группы атомов к другой.
Количество дислокаций в кристаллических структурах очень велико. Число дислокационных линий, пересекающих 1 см2 внутри отожженных монокристаллов может достигать 104¸106 и более.
Схемы образования дислокаций представлены на рис. 3.4 и рис. 3.5.
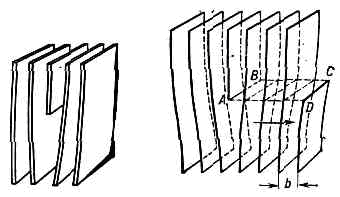
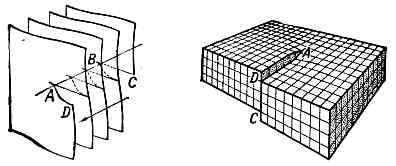
Рис. 3.4.Образование дислокаций на границах блоков:
а – два блока, растущих навстречу друг другу; б— дислокации, возникающие при срастании блоков
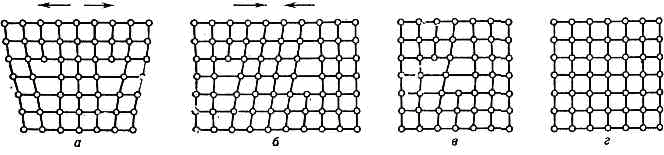
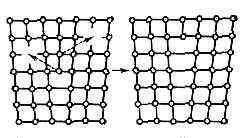
Рис. 3.5. Образование дислокаций из скопления вакансий:
Наличие дислокаций значительно снижает прочность реальных кристаллов, которые разрушаются при напряжениях, на несколько порядков меньших, чем идеальные.
Дислокации влияют на электрические, оптические, магнитные и другие свойства. Так, они повышают электросопротивление, снижают плотность, упругость, а также предельное напряжение сдвига материала. Последнее объясняется тем, что при сдвиге, т.е. при пластической деформации к имеющимся дислокациям присоединяются и вновь образованные.
Однако пластическая деформация и рост дефектов могут привести к упрочнению структуры. Это происходит в результате накопления дислокаций и взаимодействия их как между собой, так и с другими дефектами кристаллической решетки, что вызывает ее искажение и затрудняет перемещение дислокаций. Кроме того, атомы примесей, границы блоков, обособленные включения в решетки также затрудняют перемещение дислокаций, увеличивая сопротивление сдвигу.
Напрашивается вывод о положительной роли дислокаций, тем более, что в металловедении известны многие практические приемы упрочнения структуры металлов, такие как холодное деформирование (наклеп), введение примесей (легирование), создание обособленных включений (закалка) и др.
Следовательно, для упрочнения кристаллической структуры необходимо стремиться либо к большему развитию дефектов, либо к полному их устранению. На рис. 3.6 представлен график влияния роста дефектов на изменение прочности кристаллической структуры, который показывает, что максимальная прочность реальных кристаллов далека от теоретической.
Рис. 3.6. Зависимость сопротивления деформации от количества дефектов в кристалле
В продолжение освещения роли линейных дефектов, образующихся в процессе пластических деформаций в кристаллической структуре, необходимо заметить о возможности локального скопления дислокаций, которые могут вызвать местные концентрации напряжений. Последние, в сочетании с такими же локальными скоплениями дефектов, способны образовывать зародыши микротрещин, которые, как известно, являются основной причиной разрушения структуры.
Роль поверхностных и объемных дефектов в структурообразовании рассмотрим при изучении макроструктуры материалов.
ДИСЛОКАЦИИ
(от позднелат. dislocatio — смещение), дефекты кристалла, представляющие собой линии, вдоль и вблизи к-рых нарушено характерное для кристалла правильное расположение ат. плоскостей. Механические свойства кристаллов — прочность и пластичность в значительной мере обусловлены существованием Д. и их движением.
Рис. 1. Краевая дислокация: слева — обрыв ат. плоскости внутри кристалла; справа — схема образования краевой дислокации.
Простейшими видами Д. явл. краевая и винтовая Д. Краевая Д. представляет собой линию, вдоль к-рой обрывается внутри кристалла край «лишней» полуплоскости (рис. 1, слева). Её образование можно описать при помощи след. операции: надрезать кристалл по плоскости АВCD (рис. 1, справа), сдвинуть нижнюю часть относительно верхней на один период решётки 6 в направлении, перпендикулярном к АВ, а затем вновь сблизить атомы на противоположных краях разреза внизу. Вектор b, длина к-рого равна величине сдвига, наз. вектором Б ю р г е р с а. Электронные микроскопы с большой разрешающей способностью позволяют наблюдать специфичное для краевой Д. расположение ат. плоскостей, представленное на рис. 1. Плоскость, проходящая через вектор b и линию Д., наз. плоскостью скольжения.
Рис. 2. Винтовая дислокация: слева — схема образования винтовой дислокации; посредине — расположение атомов в кристалле с винтовой дислокацией (атомы располагаются в вершинах кубиков); справа — расположение атомов в плоскости ABCD.
Если вектор сдвига b не перпендикулярен, а параллелен границе надреза АВ, то получается винтовая Д. (рис. 2, слева). Винтовая Д. имеет неск. плоскостей скольжения. Кристалл с винтовой Д. фактически состоит из одной ат. плоскости, приблизительно перпендикулярной оси винтовой Д. и закрученной в виде пологого геликоида (рис. 2, посредине). В точке выхода винтовой Д. на внешнюю поверхность кристалла (рис. 2, справа) возникает ступенька AD, равная по высоте проекции вектора b на нормаль к поверхности. В процессе кристаллизации атомы в-ва, выпадающие из пара или р-ра, легко присоединяются к ступеньке, что приводит к спиральному механизму роста кристалла (рис. 3).
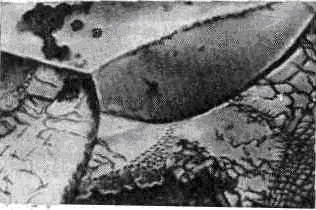
Рис. 3. Спираль роста на поверхности кристалла парафина; ступень роста обрывается в точке выхода винтовой дислокации на поверхность.
Рис. 4. Поля упругих напряжений вокруг краевых дислокаций в кристалле кремния, выявленные методом фотоупругости. Дислокации пронизывают пластинку кремния перпендикулярно к плоскости рисунка.
Между предельными случаями краевой и винтовой Д. возможны любые промежуточные. В общем случае линия Д. может представлять собой произвольную пространств. кривую, вдоль к-рой вектор Бюргерса остаётся постоянным (и равным к.-л. вектору трансляции решётки), хотя ориентация Д. может изменяться.
Линии Д. не могут обрываться внутри кристалла, они должны либо быть замкнутыми, образуя петли, либо разветвляться на неск. Д., либо выходить на поверхность кристалла.
Рис. 5. а и б — отталкивающиеся и притягивающиеся дислокации; в и г — аннигиляция притягивающихся дислокаций.
Плотность Д. в кристалле определяется как ср. число линий Д., пересекающих внутри тела площадку в 1 м2, или как суммарная длина Д. в 1 м3. Плотность Д. обычно колеблется от 106 до 107 на 1 м2 в наиб. совершенных монокристаллах и до 1015—1016 на 1 м2 в сильно искаженных (наклёпанных) металлах (см. ниже).
Участки кристалла вблизи Д. находятся в упругонапряжённом состоянии. Напряжения убывают обратно пропорц. расстоянию от Д. Поля напряжений вблизи отдельных Д. выявляются (в прозрачных кристаллах с низкой плотностью Д.) с помощью поляризов. света (рис. 4). Величина упругой энергии, обусловленной полем напряжений Д., пропорц. b2 и составляет обычно =10-13 Дж на 1 м длины Д. При сближении двух Д. с одинаковыми векторами b (рис. 5, а) упругие напряжения около Д. увеличиваются и Д. отталкиваются. При сближении Д. с противоположными векторами Бюргерса их упругие поля взаимно компенсируются (рис. 5, б, в, г); Д. притягиваются и аннигилируют.
Движение дислокаций. Поскольку Д. обладает собств. полем напряжений, она под действием внешних приложенных к кристаллу напряжений испытывает силу, под действием к-рой приходит в движение, результатом чего является взаимное «проскальзывание» ат. плоскостей —пластич. деформация.
При перемещении Д. в плоскости скольжения в каждый данный момент разрываются и пересоединяются связи не между всеми атомами на плоскости скольжения, а только между теми атомами, к-рые находятся у линии Д. (рис. 6). Поэтому пластическая деформация сдвига может происходить при сравнительно малых внеш. напряжениях. Эти напряжения на неск. порядков ниже, чем напряжение, при к-ром может пластически деформироваться совершенный кристалл без Д. путём разрыва всех межат. связей в плоскости скольжения (теор. прочность на сдвиг, ( см. ПЛАСТИЧНОСТЬ).
Движение краевых Д. по нормали к плоскости скольжения (п е р е п о л з а н и е) осуществляется путём присоединения или отрыва вакансий от края плоскости (рис. 7). Оно связано с диффузионным переносом массы, пластич. деформацией и происходит при высоких темп-рах.
Рис. 6. Перемещение дислокации в плоскости скольжения сопровождается разрывом и пересоединением межат. связей атомов у линии дислокации.
Подвижность дислокаций. Движению Д. препятствует не только прочность разрываемых межат. связей, но и рассеяние фононов и электронов проводимости в упруго искажённой области кристалла, окружающей движущиеся Д. Движению Д. мешают также упругое вз-ствие с др. Д. и с примесными атомами, межзёренные границы в поликристаллах, ч-цы др. фазы в распадающихся сплавах, двойники ( см. ДВОЙНИКОВАНИЕ) и др. дефекты в кристаллах. На преодоление этих препятствий тратится часть работы внеш. сил. Т. о., кристалл с Д. «мягче» бездефектного кристалла, но если он «набит» Д. и др. дефектами настолько, что они мешают друг другу, то кристалл снова становится «жёстким».
Рис. 7. Переползание краевой дислокации. Атомы лишней полуплоскости переходят в вакантные узлы решётки.
Образование и исчезновение дислокаций. Обычно Д. возникают при образовании кристалла из расплава или из газообразной фазы ( см. КРИСТАЛЛИЗАЦИЯ). Методы выращивания бездислокац. монокристаллов очень сложны и разработаны только для немногих в-в. После тщательного отжига кристаллы содержат обычно 108—109 Д. на 1 м2. Притягивающиеся Д. с противоположными векторами Бюргерса, лежащие в одной плоскости скольжения, при сближении уничтожают друг друга (аннигилируют, рис. 5, б, в, г). Если такие Д. лежат в разных плоскостях скольжения, то для их аннигиляции требуется переползание. Поэтому при высокотемпературном отжиге, способствующем переползанию, плотность Д. понижается. Искривление ат. плоскостей вблизи Д. изменяет сечение рассеяния рентг. лучей и эл-нов. На этом основаны рентг. и электронно-микроскопич. методы наблюдения Д. (рис. 8).
Основными механизмами размножения Д. в ходе пластич. деформации являются т. н. источники Франка — Рида и двойное поперечное скольжение. Источником Франка — Рида может служить отрезок Д., закрепленный на концах. Под приложенным напряжением он прогибается, пока не отщепится замкнутая петля Д. и восстановится исходный отрезок. При двойном поперечном скольжении точками закрепления служат концы отрезков винтовой Д., вышедшей в др. плоскость скольжения и повернувшей затем в плоскость, параллельную первичной.
Рис. 8. Электронно-микроскопич. снимок дислокац. структуры кристалла хрома после высокотемпературной деформации
Дислокационная структура деформированных кристаллов. Разрушение. С ростом пластич. деформации число Д. растёт, ср. расстояния между ними сокращаются, их поля упругих напряжений взаимно перекрываются и скольжение Д. затрудняется (деформац. упрочнение). Чтобы скольжение Д. могло продолжаться, приложенное внеш. напряжение необходимо повысить. При дальнейшем размножении Д. внутр. напряжения могут достигать значений, близких к теор. прочности. При превышении предела прочности наступает разрушение кристалла — зарождаются и растут микротрещины (рис. 9).
Рис. 9. Ат. плоскости, окаймляющие трещину в кристалле фталоцианида меди: а — электронно-микроскопич. фото/рафия (межплоскостное расстояние 12,6 А); б — схема расположения ат. плоскостей.
Влияние дислокаций на физические свойства кристаллов. Д. влияют не только на такие механич. св-ва, как пластичность и прочность, для к-рых присутствие Д. явл. определяющим, но и на др. физ. св-ва кристаллов. Напр., с увеличением плотности Д. возрастает внутреннее трение, изменяются оптич. св-ва, повышается электросопротивление металлов. Д. увеличивают ср. скорость диффузии в кристалле, ускоряют старение и др. процессы, связанные с диффузией, уменьшают хим. стойкость кристалла, так что в результате обработки поверхности кристалла спец. в-вами (травителями) в местах выхода Д. образуются видимые ямки. На этом основано выявление Д. в непрозрачных материалах методом избирательного травления (рис. 10).
Рис 10. Ряды дислокаций в плоскостях скольжения в кристалле LiF, выявленные. методом травления. Косые ряды — краевые дислокации, вертикальный ряд — винтовые.
Дислокации – основы материаловедения
Дислокации — линейные дефекты кристаллической решетки типа обрыва или сдвига атомных плоскостей, нарушающие правильность их чередования. Энергия образования дислокаций существенно выше энергии образования точечных дефектов, поэтому они не могут существовать в измеримых концентрациях как термодинамически устойчивые дефекты. Они легко образуются при выращивании монокристаллов или эпитаксиальных пленок, сопровождающемся термическими, механическими и концентрационными напряжениями, приводящими к пластической деформации кристалла. Часть дислокаций может сохраняться в кристалле даже после самого тщательного отжига. Более подробно вопрос о причинах возникновения дислокаций будет рассмотрен при обсуждении методов выращивания монокристаллов и эпитаксиальных пленок (см. гл. 6
Рис. 3.4. а — Схема образования краевой дислокации. б — Расположение атомов вокруг краевой дислокации в простой кубической решетке.
и гл. 9), так как он имеет огромное значение для технологии полупроводников.
Поскольку дислокации при небольших концентрациях распределены по объему кристалла неравномерно, то нарушения свойств кристалла, обусловленные их присутствием, локализованы в небольших объемах, окружающих дислокации. Следовательно, кинетика процессов, протекающих вблизи этих дефектов, будет иной, чем в объеме кристалла, где дислокации отсутствуют.
Различают простые и смешанные дислокации. К простым дислокациям относят краевые и винтовые.
Рассмотрим кристалл, в котором в результате приложения внешних сил одна часть начинает смещаться относительно другой по некоторой плоскости (плоскости скольжения) вдоль некоторого выбранного направления (направления сдвига), то есть кристалл подвергается пластической деформации сдвига путем скольжения (рис. 3.4,а). Перемещения атомов по плоскости скольжения не являются равномерными, так как сдвиг на единицу скольжения происходит только в одной части кристалла, а в остальной части сдвиг полностью отсутствует. Перпендикулярную направлению сдвига линию AD, расположенную внутри кристалла и являющуюся границей между этими двумя частями кристалла, называют линией краевой дислокации и обозначают ⊥. Расположение атомов внутри деформированного скольжением кристалла в плоскости, перпендикулярной линии AD, имеет вид, изображенный на рис. 3.4,б. Атом, расположенный непосредственно над знаком дислокации ⊥, имеет окружение, отличающееся от окружения атомов в бездефектной части кристалла. Все происходит так, как если бы в объеме кристалла появилась
Рис. 3.5. Схема образования винтовой дислокации.
одна «лишняя» атомная плоскость, край которой обрывается внутри кристалла. Краевая дислокация, таким образом, представляет собой дефект, при котором одна из атомных плоскостей обрывается внутри кристалла по линии краевой дислокации AD, перпендикулярной направлению сдвига. Краевые дислокации образуются вдоль плоскостей скольжения. Условно подразделяют краевые дислокации на положительные и отрицательные. Положительная дислокация соответствует случаю, когда «лишняя» атомная плоскость находится сверху над знаком ⊥ (рис. 3.4,б) и в
верхней половине кристалла действуют сжимающие напряжения, в ниж
ней — растягивающие; а отрицательная — случаю, когда «лишняя» атомная плоскость находится снизу под знаком ⊥, то есть верхняя половина
кристалла растянута, а нижняя сжата.
Сдвиг одной части кристалла относительно другой, возникающий под влиянием внешних воздействий, может деформировать кристалл таким образом, что его можно представить состоящим из атомных плоскостей, закрученных в виде винтовой лестницы, ось которой и образует линию винтовой дислокации AD (рис. 3.5 и рис. 3.6). Винтовая дислокация
обозначается ⊗. Линия винтовой дислокации характеризуется тем, что
она параллельна направлению сдвига. При каждом обходе вокруг нее
мы поднимаемся или опускаемся на одно межплоскостное расстояние (рис. 3.6). Выход винтовой дислокации на поверхность кристалла заканчивается незарастающей ступенькой. В отличие от краевой дислокации, винтовая дислокация не имеет «лишних» плоскостей и может образовываться при сдвиге по любой атомной плоскости, проходящей через линию дислокации AD, то есть она не определяет однозначно плоскость скольжения. Различают правые и левые винтовые дислокации, причем направление вращения играет ту же роль, что и знак у краевых дислокаций.
Следует отметить, что в кристаллах полупроводников в чистом виде краевая и винтовая дислокации встречаются редко. Как правило, они по
Рис. 3.6. а — Винтовая дислокация. б — Расположение атомов на винтовой поверхности вдоль винтовой дислокации.
являются одновременно, приводя к образованию смешанных форм, при этом линия результирующей дислокации (граница между сдвинутой и не сдвинутой частями кристалла) не обязательно должна быть прямой, она может представлять собой произвольную кривую. Криволинейную дислокацию произвольной формы, которую можно представить как состоящую из различных комбинаций «чистых» краевой и винтовой дислокаций, называют смешанной. На рис. 3.7 показана смешанная дислокация в простой кубической решетке.
Основной характеристикой дислокации является вектор Бюргерса (вектор сдвига) b. Вектор Бюргерса — это мера искажений решетки, обусловленных присутствием дислокации. Для его определения строят замкнутый контур в кристалле с дефектом и контур, проходящий через те же атомы, в кристалле без дефекта. Проведем в решетке, содержащей краевую дислокацию, замкнутый контур A-B-C-D-A вокруг этой дислокации, начав его из произвольно взятого узла A и откладывая против часовой стрелки определенное число межатомных расстояний (рис. 3.8). Если построить тот же контур в решетке без дислокации, откладывая такое же число межатомных расстояний, то контур окажется незамкнутым. Вектор b, который необходимо добавить, чтобы замкнуть контур, и есть вектор Бюргерса. Величина разрыва контура характеризует сумму всех упругих смещений решетки, накопившихся в области вокруг дислокации. Для примера, изображенного на рис. 3.8 (простая кубическая решетка), вектор Бюргерса по абсолютной величине равен расстоянию между соседними атомами и ориентирован перпендикулярно линии дислокации.
Аналогичное построение для винтовой дислокации в простой кубиче
Рис. 3.7. a — Сдвиг, создавший смешанную дислокацию. б — Смешанная дислокация в простой кубической решетке. Краевая плоскость скольжения совпадает с плоскостью чертежа; черные кружки — атомы под плоскостью скольжения, белые — атомы над ней; заштрихованный участок — ступенька, образовавшаяся в результате сдвига.
Рис. 3.8. Контур и вектор Бюргерса краевой дислокации.
ской решетке показывает, что и в этом случае b равен расстоянию между соседними атомами (это шаг винта в направлении линии дислокации), но направлен вдоль линии дислокации.
Вектор Бюргерса — наиболее инвариантная характеристика дислокации. Он остается постоянным вдоль всей линии любой дислокации и сохраняется при ее движении [27].
Теперь можно дать определение простых дислокаций через вектор Бюргерса. Краевой дислокацией называют дислокацию, вектор Бюргерса b которой перпендикулярен линии краевой дислокации. Винтовой дислокацией называют дислокацию, вектор Бюргерса b которой параллелен линии винтовой дислокации. В общем случае смешанной дислокации вектор Бюргерса может иметь иные направления относительно линии дислокации.
Дислокации окружены полями упругих напряжений. Область над линией краевой дислокации, содержащая лишнюю полуплоскость, испытывает напряжения сжатия, область под линией дислокации — напряжения растяжения. Вокруг винтовых дислокаций существует поле сдвиговых (касательных) напряжений. Величина напряжений убывает обратно пропорционально расстоянию от линии дислокации [27].
Источник: И. А. Случинская, Основы материаловедения и технологии полупроводников, Москва — 2002
Дислокации в кристаллах
Наиболее распространена так называемая смешанная дислокация, которая является любой комбинацией краевой и винтовой дислокаций. Возле линий дислокаций структура кристалла деформируется с затуханием искажения обратно пропорционально расстоянию от этой линии.
Во всякой дислокации существуют недостаточно компенсированные межатомные связи. С ними и с полем деформации около дислокации связано локальное повышение внутренней энергии и энтропии атомов на дислокации и около неё. Величина внутренней энергии дислокации пропорциональна длине дислокации и квадрату вектора Бюргерса.
Дислокации, как и точечные дефекты, могут перемещаться по кристаллической решётке. Однако движение дислокаций связано с большими ограничениями, так как дислокация всегда должна быть непрерывной линией. Возможны два основных вида движений дислокаций: переползание и скольжение. Переползание дислокаций происходит благодаря добавлению или удалению атомов из лишней полуплоскости, что может происходить вследствие диффузии. При скольжении дислокации лишняя полуплоскость, занимавшая определённое положение в кристаллической решётке, соединяется с атомной плоскостью, находящейся под плоскостью скольжения, а соседняя атомная плоскость становится тогда лишней полуплоскостью. Такое плавное скольжение линии дислокации вызывается действием напряжений сдвига, приложенных к поверхности кристалла.
Методы изучения дислокаций
Фотографии структуры кристаллов с имеющимися в них дефектами можно получить с помощью ионного проектора и электронного микроскопа. При изучении дефектов кристаллов используют также метод протравливания: на поверхность кристалла наносят химические травители, которые наиболее активно взаимодействуют с теми областями кристалла, в которых сосредоточены наибольшие искажения, вызванные дислокациями. В результате такого травления на поверхности кристалла (или среза кристалла) появляются ямки, свидетельствующие о наличии дислокации в этом месте. Ямки рассматривают в обычный оптический микроскоп. Таким способом можно определить плотность дислокаций.