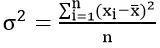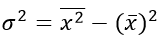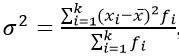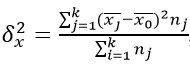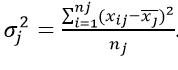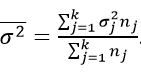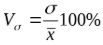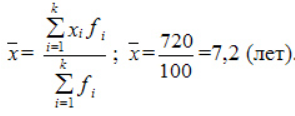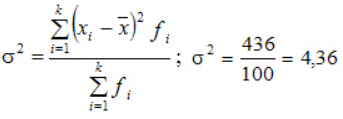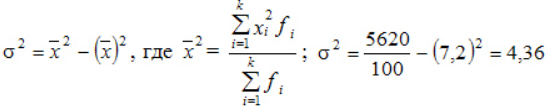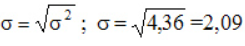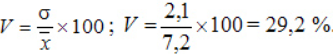Дисперсия для чего нужна

Что такое дисперсия в статистике

Статистика, в частности, оперирует рядами данных, характеризующих какой-либо признак, явление. Интересует их изменение.

Вариация представляет собой отличие величин одинакового показателя у разных предметов. Ее изучение позволит понять причины отклонений от нормы, анализировать их и в какой-то мере прогнозировать. Также станет возможным выявить факторы, влияющие на значения, отсеяв случайные.

Характеристики равномерного распределения представлены на картинке:

При значительном объеме статистики, средняя величина очевидно близка к нормальной. Об этом говорят и законы распределения. Отклонения от нее будут являться объективной характеристикой.

Только вот отрицательные значения этих разбросов будут сбивать с толку при расчетах, погашая положительные. А оставлять лишь модули – для математика не корректно. Напрашивается возвести в четную степень, а именно – во вторую.

Решение оказалось не только удобным. Оно открыло бо́льшие возможности в изучении отклонений. А важны именно они, поскольку сама по себе средняя мало что дает.

В качестве одного из важных показателей вариации, вводится понятие «дисперсия» – усредненный квадрат отклонений численных значений каких-либо событий от средней величины.

Никакого наглядного смысла величина не несет. Другое дело, среднее квадратическое отклонение – корень квадратный из дисперсии.

Виды дисперсии дискретной случайной величины

Для анализа данных цифр в таком виде недостаточно. Гораздо больше можно выжать из последовательности, если разбить ее на группы по определенному признаку.

Общая дисперсия

Как можно заметить, вычисленная по приведенному выше определению величина характеризует отклонения в целом. Без учета определяющих вариацию факторов. Вернее, с учетом всех, включая совершенно случайные. Поэтому и называется «общей» и рассчитывается по формулам, указанным ниже.

Простая дисперсия, без разделения на группы:

Или в несколько преобразованном виде:

Взвешенная дисперсия, для вариационного ряда:

где x_i – значение из ряда;

f_i – частота, количество повторений;

n – число вариантов.

Черта сверху указывает на среднюю величину.

Межгрупповая дисперсия

Характеризует систематическое отклонение, возникающее из-за фактора, по которому производилось выделение признаков в группы. Поэтому также называется «факторной».

Как найти данную дисперсию? По формуле:

где k – количество групп;

n_j – элементов в группе с индексом j.

Внутригрупповая дисперсия

Возникает по хаотичной причине, не связанной с причиной сделанной выборки. Неучтенный фактор. Еще обозначается как «остаточная».

Например, рассматривается количество выпущенных деталей за месяц каждым фрезеровщиком цеха.

В качестве критерия отбора в группу выбираем возраст оборудования. Он-то и не будет влиять на производительность внутри подборки: там станки у всех практически одинаковые.

Если вычислить среднюю величину от всех групповых,

то получим характеристику случайного разброса. Иными словами, составляющую вариации, зависящую от чего угодно, кроме фактора отбора.

Взаимосвязь

В соответствии с правилом сложения, общая D[X] включает средние выражения остаточной и факторной. И это логично, поскольку учитывает и случайное изменение в группе, и систематическое в факторной.

Свойства дисперсии

Если последовательность состоит из одинаковых чисел, то D[X] будет нулевой.

Уменьшение всех значений на постоянную величину на дисперсию не влияет. Иначе говоря, рассчитать σ 2 можно по отклонениям от фиксированного числа.

Уменьшение всех цифр в k раз приведет к падению D[X] в k 2 раз. Можно, например, иметь в виду значения в метрах, а результат вычислить в футах. Достаточно учесть один раз то, на что следует умножить.

Показатели вариаций

Кроме размаха (разницы максимального и минимального значений), среднего линейного и дисперсии, изменения описываются коэффициентом вариации:

Оценить масштаб разброса проще по относительной величине. Тем более, что измеряются в одних единицах.

Пример расчета дисперсии

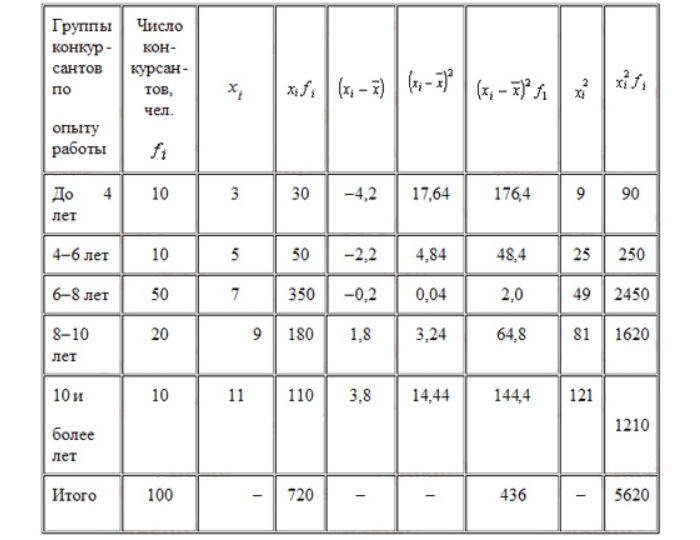
Компания объявила конкурсный отбор для приема сотрудников. В качестве критерия принят стаж работы по специальности. Приведем исходные данные и расчеты.

По альтернативной формуле:

Заключение

Статистика оперирует значительными объемами данных. Вариация, как одно из основных понятий – не исключение. И дисперсия в качестве основной характеристики.

Для упрощения расчетов существует масса онлайн калькуляторов. Имеется упомянутый инструмент в MS Excel.

Источник

Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации в Excel

Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.

Дисперсия

Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.

Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.

Формула дисперсии в теории вероятностей имеет вид:

То есть дисперсия — это математическое ожидание отклонений от математического ожидания.

На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:

s 2 – выборочная дисперсия, рассчитанная по данным наблюдений,

X – отдельные значения,

X̅– среднее арифметическое по выборке.

Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.

Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.

Расчет дисперсии в Excel

Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.

В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.

Свойства дисперсии

Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).

Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А 2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.

Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.

Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.

Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.

Среднеквадратичное (стандартное) отклонение

Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:

На практике формула стандартного отклонения следующая:

Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.

Расчет cреднеквадратичного (стандартного) отклонения в Excel

Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).

Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.

Коэффициент вариации

Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:

По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.

Расчет коэффициента вариации в Excel

Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:

Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:

Коэффициент осцилляции

Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.

Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.

Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.

Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.

Источник

Дисперсия

Дисперсия и среднеквадратическое (стандартное) отклонение – самые распространенные статистические механизмы для измерения и описания разброса того или иного распределения. Дисперсия обычно обозначается символом σ2 и отражает, насколько далеко от среднего значения расположены наблюдения в рамках того или иного распределения.

Инвестиции в акции США, IPO и Pre-IPO

При этом расстояние (разница) между каждым наблюдением и средним значением возводится в квадрат; сумма таких составляющих, возведенных в квадрат, затем делится на количество наблюдений.

Поскольку разница между каждым членом и средним значением возводится в квадрат, формула для вычисления дисперсии присваивает определенный вес наблюдениям, которые расположены вдали от среднего значения (то есть «отщепенцам»), как показано в приведенной ниже таблице роста учащихся.

Средний рост обеих групп учащихся составляет 70 дюймов. Суммы абсолютных отклонений от среднего значения в обеих группах также одинаковы – 14 дюймов. По этому показателю разброса указанные два распределения идентичны.

Однако дисперсия для группы 2 оказалась выше из-за веса, присвоенного в формуле дисперсии значениям, которые расположены особенно далеко от среднего значения (в нашем случае эти значения относятся к Сахару и Нарцисо).

Дисперсия сама по себе редко используется в качестве описательной статистики. В наибольшей степени она полезна для определения среднеквадратического (стандартного) отклонения, которое вычисляется как корень квадратный из дисперсии.

Из книги Чарльза Уилана “Голая статистика. Самая интересная книга о самой скучной науке”.

Источник

Дисперсия

Опубликовано 25.12.2020 · Обновлено 07.01.2021

Что такое дисперсия?

Ключевые моменты

Понимание дисперсии

В статистике, дисперсия измеряет изменчивость от среднего или среднего. Он рассчитывается путем взятия разностей между каждым числом в наборе данных и среднего, затем возведения разностей в квадрат, чтобы сделать их положительными, и, наконец, деления суммы квадратов на количество значений в наборе данных.

Дисперсия рассчитывается по следующей формуле:

вариансе σ2знак равно∑язнак равно1п(Икся-Иксˉ)2пжчере:Иксязнак равнотче ятчас Дата поинтИксˉзнак равнотче месп оеллдтроянты пзнак равнотче нутбер ое дтроянты \ begin & \ text \ sigma ^ 2 = \ frac <\ sum_ ^ n <\ left (x_i – \ bar \ right) ^ 2>> \ \ & \ textbf <где:>\\ & x_i = \ text i ^

\ text \\ & \ bar = \ text <среднее значение всех точек данных>\\ & n = \ text <количество точек данных>\\ \ end <выровнено>Взаимодействие с другими людьмидисперсия σ2знак равноп

Большой разброс указывает на то, что числа в наборе далеки от среднего и далеко друг от друга. С другой стороны, небольшая разница указывает на обратное. Однако нулевое значение дисперсии указывает на то, что все значения в наборе чисел идентичны. Любая отличная от нуля дисперсия – положительное число. Разница не может быть отрицательной. Это потому, что это математически невозможно, поскольку в результате квадрата невозможно получить отрицательное значение.

Особые соображения

Вы также можете использовать приведенную выше формулу для расчета дисперсии в областях, отличных от инвестиций и торговли, с некоторыми небольшими изменениями. Например, при вычислении дисперсии выборки для оценки дисперсии генеральной совокупности знаменатель уравнения дисперсии становится N – 1, чтобы оценка была несмещенной и не занижала дисперсию генеральной совокупности.

Преимущества и недостатки дисперсии

Статистики используют дисперсию, чтобы увидеть, как отдельные числа соотносятся друг с другом в наборе данных, вместо того, чтобы использовать более широкие математические методы, такие как распределение чисел по квартилям. Преимущество дисперсии заключается в том, что она рассматривает все отклонения от среднего одинаково независимо от их направления. Сумма квадратов отклонений не может быть равна нулю, и это создает впечатление отсутствия изменчивости данных.

Однако одним из недостатков дисперсии является то, что она придает дополнительный вес выбросам. Это числа, далекие от среднего. Возведение этих чисел в квадрат может исказить данные. Еще одна ловушка использования дисперсии заключается в том, что ее нелегко интерпретировать. Пользователи часто используют его в первую очередь для извлечения квадратного корня из его значения, которое указывает стандартное отклонение набора данных. Как отмечалось выше, инвесторы могут использовать стандартное отклонение, чтобы оценить, насколько стабильна прибыль с течением времени.

Краткая справка

В некоторых случаях риск или волатильность могут быть выражены как стандартное отклонение, а не как дисперсия, поскольку первое часто легче интерпретировать.

Пример отклонения

Возведение этих отклонений в квадрат дает 25%, 225% и 400% соответственно. Если мы сложим эти квадраты отклонений, мы получим 650%. Если разделить сумму в 650% на количество возвратов в наборе данных – в данном случае три, – получится дисперсия 216,67%. Извлечение квадратного корня из дисперсии дает стандартное отклонение доходности 14,72%.

Источник

Научный форум dxdy

Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки

Правила форума

В этом разделе нельзя создавать новые темы.

Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».

Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.

Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.

Зачем нужна дисперсия?

Последний раз редактировалось mustitz 04.10.2012, 14:27, всего редактировалось 2 раз(а).

Больше разброс, больше риск. Количество денег на руках не бесконечно.

Простой пример, ты продаешь дом и вкладываешь 100k долларов в некоторое мероприятие. Допустим, в одном случае ты получаешь фиксировано 110k, а в другом случае ты с вероятностью 45% деньги теряешь и бомжуешь до конца жизни, а с вероятностью 55% получаешь 200k долларов. Математическое ожидание одинаково, а вот дисперсия нет.

Заслуженный участник

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Источник