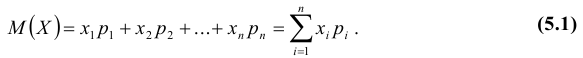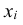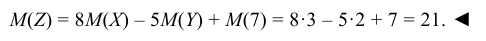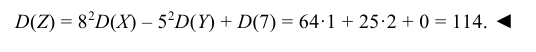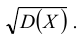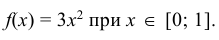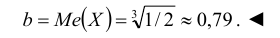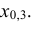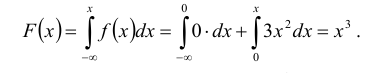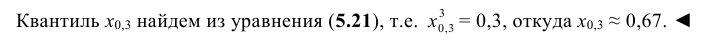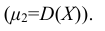Дисперсия случайной величины х равна 5 чему равно значение дисперсии d 2x
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Верный ответ: 1 Вариантов ответов: 3
ВОПРОС N 2094. Математическое ожидание случайной величины X равна 5: М(X) = 5. Чему равно
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Верный ответ: 1 Вариантов ответов: 4
ВОПРОС N 2095. Математическое ожидание случайной величины X равна 5: М(X) = 5. Чему равно
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Верный ответ: 3 Вариантов ответов: 5
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Верный ответ: 3 Вариантов ответов: 4
ВОПРОС N 2097. Найти математическое ожидание дискретной случайной величины X, заданной
следующим законом распределения:
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Верный ответ: 1 Вариантов ответов: 4
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
1. Математическое ожидание.
Верный ответ: 2 Вариантов ответов: 4
ВОПРОС N 2101. Чему равна дисперсия суммы D(X+Y) двух независимых случайных величин X и Y,
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Верный ответ: 3 Вариантов ответов: 5
ВОПРОС N 2102. Чему равна дисперсия разности D(X-Y) двух независимых случайных величин X и Y,
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Верный ответ: 3 Вариантов ответов: 5
ВОПРОС N 2103. Дисперсия случайной величины X равна 5: D(X) = 5. Чему равно значение дисперсии
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Верный ответ: 2 Вариантов ответов: 3
ВОПРОС N 2104. Дисперсия случайной величины X равна 5: D(X) = 5. Чему равно значение дисперсии
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Верный ответ: 4 Вариантов ответов: 4
ВОПРОС N 2105. Дисперсия случайной величины X равна 5: D(X) = 5. Чему равно значение дисперсии
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Верный ответ: 4 Вариантов ответов: 5
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Верный ответ: 1 Вариантов ответов: 4
ВОПРОС N 2110. Среднее квадратическое отклонение равно:
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
1. квадрату дисперсии;
2. корню квадратному из дисперсии;
3. квадрату математического ожидания;
4. корню квадратному из математического ожидания.
Верный ответ: 2 Вариантов ответов: 4
Дата добавления: 2015-01-12 ; просмотров: 407 | Нарушение авторских прав
Дисперсия формула
Содержание:
Разность 
называется отклонением случайной величины А от ее математического ожидания М(Х). Математическое ожидание отклонения равно нулю:
Дисперсией, или рассеянием, случайной величины X называется математическое ожидание квадрата ее отклонения:
Из определения и свойств математического ожидания следует, чтс дисперсия любой случайной величины неотрицательна, т.е.
Для вычисления дисперсии применяется формула
По этой ссылке вы найдёте полный курс лекций по теории вероятности:
Дисперсия случайной величины обладает следующими свойствами:
1. Дисперсия постоянной величины равна нулю:
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
4. Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий:
5. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:
Возможно вам будут полезны данные страницы:
Свойство 3 распространяется на п независимых случайных величин:
Дисперсия дискретной случайной величины с законом распределения
— другое обозначение для математического ожидания. Этим обозначением будем пользоваться и в дальнейшем, в зависимости от обстоятельств.
Если дискретная случайная величина принимает бесконечную по-следовательность-значений с законом распределения
то ее дисперсия определяется формулой
при условии, что этот ряд сходится.
Дисперсия непрерывной случайной величины X, все значения которой принадлежат отрезку 
определяется формулой
Дисперсию можно вычислять по формуле
Дисперсия непрерывной случайной величины X, все значения которой принадлежат отрезку 
, определяется формулой
если этот несобственный интеграл сходится.абсолютно.
Средним квадратическим отклонением, или стандартным отклонением, случайной величины X называется корень квадратный из ее дисперсии:
Это определение имеет смысл, поскольку выполнено условие (2.5.3).
Пример с решением
Пример 1.
Доказать формулы (2.5.1) и (2.5.4).
Решение:
равенство (2.5.1) доказано.
Учитывая свойства математического ожидания, получаем
равенство (2.5.4) доказано.
Пример 2.
Решение:
Принимая во внимание определение дисперсии и тот факт, что математическое ожидание постоянной равно этой постоянной, получаем
Из определения дисперсии и свойств математического ожидания следует, что
Для доказательства формулы (2.5.8) воспользуемся формулой (2.5.4):
Равенство (2.5.8) следует из формул (2.5.6) и (2.5.7):
Пример 3.
Дискретная случайная величина X имеет закон распределения
Найти дисперсию и среднее квадратическое отклонение случайной величины X.
Решение:
По формуле (2.4.3) находим
Запишем закон распределения квадрата отклонения этой величины, т.е. величины 
По формуле (2.5.10) получаем
В соответствии с формулой (2.5.16) находим среднее квадратическое отклонение
Замечание. Дисперсию можно вычислить и по формуле (2.5.4). Найдем для этого математическое ожидание квадрата случайной величины X, предварительно записав закон распределения случайной величины X 2 ;
По формуле (2.4.3) находим
В соответствии с формулой (2.5.4) находим
Пример 4.
Закон распределения дискретной случайной величины X задан таблицей
Вычислить дисперсию случайной величины X по формуле (2.5.4) и по формуле (2.5.10).
Решение:
Сначала найдем математическое ожидание случайной величины^:
Запишем закон распределения случайной величины 
и найдем дисперсию случайной величины Xпо формуле (2.5.10):
Квадраты значений случайной величины X равны: 
,
, т.е. величина 
принимает значения 
Закон распределения случайной величины X2 можно записать в виде:
По формуле (2.4.3) находим
Следовательно, по формуле (2.5.4) имеем
Пример 5.
Симметричная монета подбрасывается 4 раза. Случайная величина X- «число выпадений герба при этих подбрасываниях». Найти числовые характеристики случайной величины 
Решение:
Данная дискретная случайная величина X может принимать пять значений: 
.
Закон распределения случайной величины X можно задать таблицей Находим математическое ожидание 
Закон распределения случайной величины 
имеет вид:
Вычислим дисперсию 
и среднее квадратическое отклонение 
:
Пример 6.
Решение:
Запишем сначала закон распределения этой случайной величины в виде таблицы
Найдем математические ожидания 
:
Дисперсию вычислим по формуле (2.5.4):
Пример 7.
Даны все возможные значения дискретной случайной величины 
а также известны 
Найти закон распределения случайной величины X
Решение:
где 
пока неизвестны, причем 
Используя условие, получаем систему двух уравнений с тремя неиз-вестными
Поскольку 
то система уравнений принимает вид
откуда 
. Поэтому 
Итак, закон распределения случайной величины X определяется таблицей
Пример 8.
Дискретная случайная величина X может принимать только два значения 
, причем 
. Известны вероятность 
математическое ожидание 
и дисперсия 
Найти закон распределения дискретной случайной вели-чиньгЛ.
Решение:
Поскольку 
(см. формулу (2.1.2)) и 
то 
откуда 
. По формуле (2.5.12) находим
Решая систему уравнений
и учитывая условие 
получаем 
Следовательно,
Пример 9.
Найти числовые характеристики 
непрерывной случайной величины X, заданной плотностью распределения
Решение:
Сначала находим М(Х) по формуле (2.4.7):
В соответствии с формулой (2.5.13) найдем D(X) :
По формуле (2.5.16) находим
Пример 10.
Найти числовые характеристики 
непрерывной случайной величины X, заданной плотностью вероятностей
Решение:
С помощью формулы (2.4.7) находим математическое ожидание:
По формулам (2.5.13) и (2.5.16) соответственно получаем
Пример 11.
Случайная величина X задана функцией распределения
Найти числовые характеристики случайной величины 
Решение:
Сначала найдем плотность распределения р(х) с помощью формулы (2.3.5). Так как 
, то
По формуле (2.4.7) вычисляем математическое ожидание:
В соответствии с формулами (2.5.13) и (2.5.16) находим дисперсию и среднее квадратическое отклонение:
Пример 12.
Независимые случайные величины 
имеют одинаковые распределения, для них
при 
Найти числовые характеристики среднего арифметического этих случайных величин, т.е. случайной величины
С учетом формулы (2.4.13) и условия (I) находим
т.е. математическое ожидание среднего арифметического п независимых одинаково распределенных случайных величин равно математическому ожиданию каждой из этих величин.
Учитывая формулы (2.5.6), (2.5.9) и условие (I), получаем
т.е. дисперсия среднего арифметического п независимых одинаково распределенных случайных величин в л раз меньше дисперсии каждой из этих величин.
Учитывая определение и условие (I), находим
Таким образом, среднее квадратическое отклонение среднего арифметического n независимых одинаково распределенных случайных величин в 
раз меньше среднего квадратического отклонения каждой величины.
Лекции:
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Содержание:
Числовые характеристики случайных величин:
Как мы уже выяснили, закон распределения полностью характеризует случайную величину, так как позволяет вычислить вероятности любых событий, связанных с этой случайной величиной. Однако, во-первых, закон распределения не всегда известен, а, во-вторых, для решения многих практических задач совсем необязательно знать закон распределения. Достаточно знать отдельные числовые характеристики, которые в сжатой, компактной форме выражают наиболее существенные черты распределения.
Например, можно составить законы распределения двух случайных величин – числа очков, выбиваемых двумя стрелками, – и выяснить, какой из двух стрелков стреляет лучше. Однако, даже не зная законов распределения, можно сказать, что лучше стреляет тот, кто в с р е д н е м выбивает большее количество очков. Таким средним значением случайной величины является математическое ожидание.
Математическое ожидание случайной величины
Определение: Математическим ожиданием, или средним значением, M(X) д и с к р е т н о й случайной величины X называется сумма произведений всех ее значений на соответствующие им вероятности: 
Заменим в формуле для дискретной случайной величины знак суммирования по всем ее значениям знаком интеграла с бесконечными пределами, дискретный аргумент xi – непрерывно меняющимся 
Рассмотрим свойства математического ожидания.
Пример:
Найти математическое ожидание случайной величины Z = 8X – – 5Y + 7, если известно, что M(X) = 3, M(Y) = 2.
Решение:
Используя свойства 1, 2, 3 математического ожидания, находим 
Итак, мы установили, что математическое ожидание является важной числовой характеристикой случайной величины. Однако одно лишь математическое ожидание не может в достаточной степени характеризовать случайную величину. Вернемся к задаче о стрелках. При равенстве средних значений числа выбиваемых очков, вопрос о том, какой из стрелков стреляет лучше, остается открытым. Однако в этом случае можно сделать предположение, что лучше стреляет тот стрелок, у которого отклонения числа выбитых очков от среднего значения меньше.
Мерой рассеяния значений случайной величины вокруг ее математического ожидания служит дисперсия (слово дисперсия означает «рассеяние).
Дисперсия случайной величины
Определение: Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания: 
Для дискретной случайной величины X эта формула принимает вид: 
Для непрерывной случайной величины: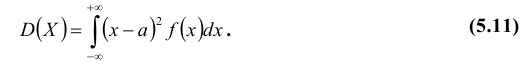 
На практике для вычисления дисперсии часто удобно пользоваться следующей теоремой.
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания: 
Для дискретной случайной величины X эта формула принимает вид: 
Для непрерывной случайной величины: 
Рассмотрим свойства дисперсии.
Пример №1
Найти дисперсию случайной величины Z = 8X – 5Y + 7, если известно, что D(X) = 1, D(Y) = 2.
Решение:
Используя свойства дисперсии, находим 
Среднее квадратическое отклонение случайной величины
Дисперсия D(X) имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину
Определение: Средним квадратическим отклонением (или стандартным отклонением) σ(Х) случайной величины Х называют значение квадратного корня из ее дисперсии: 
Свойства среднего квадратического отклонения вытекают из свойств дисперсии.
Мода и медиана. Квантили
Кроме математического ожидания, дисперсии и среднего квадратического отклонения, в теории вероятностей применяется еще ряд числовых характеристик, отражающих те или иные особенности распределения.
Определение: Модой Мо(Х) случайной величины Х называется ее наиболее вероятное значение (для которого вероятность pi или плотность вероятности f(x) достигает максимума).
Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным.
Определение: Медианой Ме(Х) непрерывной случайной величины Х называется такое ее значение, для которого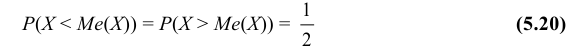 
т. е. вероятность того, что случайная величина Х примет значение, меньшее медианы или большее ее, одна и та же и равна 1/2. Геометрически вертикальная прямая х = Ме(Х), проходящая через точку с абсциссой, равной Ме(Х), делит площадь фигуры под кривой распределения на две равные части. Очевидно, что в точке х = Ме(Х) функция распределения равна 1/2.
Пример №2
Найти моду, медиану случайной величины Х с плотностью вероятности 
Решение:
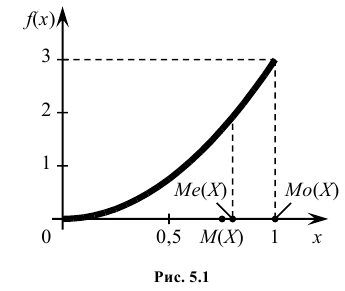
Кривая распределения представлена на рис. 5.1 Очевидно, что плотность вероятности максимальна при х= Мо(Х) = 1. Медиану Ме(Х) = найдем из условия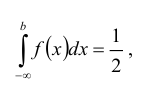 
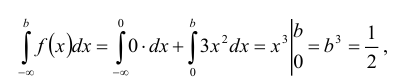
или 
откуда 
Наряду с модой и медианой для описания случайной величины используется понятие квантиля.
Определение: Квантилем уровня q (или q-квантилем) называется такое значение хq случайной величины, при котором функция ее распределения принимает значение, равное q, т. е. 
Пример №3
По данным примера 5.3 найти квантиль 
Решение:
Находим функцию распределения 
Моменты случайных величин. Асимметрия и эксцесс
Среди числовых характеристик случайной величины особое место занимают моменты – начальные и центральные.
Определение: Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени этой величины: 
Для дискретной случайной величины формула начального момента имеет вид: 
Для непрерывной случайной величины: 
Определение: Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени отклонения случайной величины Х от ее математического ожидания: 
Для дискретной случайной величины формула центрального момента имеет вид:
Для непрерывной случайной величины: 
Нетрудно заметить, что при k = 1 первый начальный момент случайной величины Х есть ее математическое ожидание
при k = 2 второй центральный момент – дисперсия 
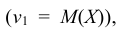
Т.е. первый начальный момент характеризует среднее значение распределения случайной величины Х; второй центральный момент – степень рассеяния распределения Х относительно математического ожидания. Для более подробного описания распределения служат моменты высших порядков.
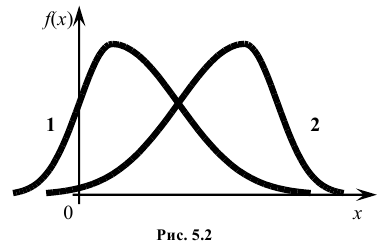
Третий центральный момент μ3 служит для характеристики ассиметрии (т.е. скошенности ) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, ее делят на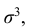 
, где σ – среднее квадратическое отклонение случайной величины Х.
Полученная величина А называется коэффициентом асимметрии случайной величины: 
Если распределение симметрично относительно математического ожидания, то коэффициент асимметрии равен нулю А = 0.
На рис. 5.2 показаны две кривые распределения 1 и 2. Кривая 1 имеет положительную (правостороннюю) асимметрию (А > 0), а кривая 2 – отрицательную (левостороннюю) асимметрию (А
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.