Длина отрезка bc на рисунке равна известно что точка м середина отрезка

18.04.202219.04.2022 admin 0 Comments

Докажите, что DM = MC.

Решение смотри на фото.

Расстояние между серединами отрезков AM и NB равно d.

Найдите AB и расстояние между серединами отрезков AM и MN.

Чему равна длина отрезка AD?

Даны два пересекающихся отрезка (см?

Даны два пересекающихся отрезка (см.

Докажите, что треугольник ABK = треугольнику ACE, если точка А является серединой отрезка ВС и серединой отрезка ЕК.

Отрезки AD и ВК пересекаются в точке С?

Отрезки AD и ВК пересекаются в точке С.

Точка С середина отрезков AD и BK.

Докажите что треугольник АBC = треугольнику DKC.

На рис?

Докажите, что треугольники BOC и AOD равны.

Докажите что любая точка прямой, проведенной перпендикулярно к отрезку через его середину, одинаково удалена от концов данного отрезка?

Докажите что любая точка прямой, проведенной перпендикулярно к отрезку через его середину, одинаково удалена от концов данного отрезка.

На рисунке ∠А = ∠В, точка О середина отрезка АВ?

На рисунке ∠А = ∠В, точка О середина отрезка АВ.

Картинка не правильная по условию решать!

Отрезки EF и РД пересекаются в их середине М?

Отрезки EF и РД пересекаются в их середине М.

Докажите, что PE || ДF.

На рисунке точка M является серединой отрезков АС и BD?

На рисунке точка M является серединой отрезков АС и BD.

Докажите, что прямые BC и AD параллельны.

В, так как это прямая и она имеет начало но не имеет конца, а если 2 прямые значит одна точка на каждой.

Проведи 2 прямые так, чтобы они пересеклись и получиться одна общая точка.

АВ = 3 * 2 = 6 см (т. К. медиана в прямоугольном треугольнике, проведенная из прямого угла, равна половине гипотенузы).

Решение смотри на фото.

AB = CD = 5 CP = BC = AD = 4( угол CBP = углу CPB как внутренние накрест лежащие) значит P = 4 + 4 + 5 + 5 = 18.

Назовем стороны a, b, c, d P = a + b + c + d a = a b = a + 3 c = a + 4 d = a + 5 P = a + (a + 3) + (a + 4) + (a + 5) P = 8 см = 80 мм (по условию) 80 = 4a + 12 68 = 4a a = 17 Стороны равны : a = 17 мм b = 20 мм c = 21 мм d = 22мм.

KB⊥BC, AD||BC = > KB⊥AD, ∠BKD = 90 BO = OD (диагонали параллелограмма точкой пересечения делятся пополам) KO = OD (медиана, проведенная из вершины прямого угла, равна половине гипотенузы) ∠BEK = ∠EKD, ∠EBD = ∠BDK (накрест лежащие углы при AD||BC) △BO..

S = 1 / 2 * 12 * a = 1 / 2 * 15 * b = 1 / 2 * c * 20 S = 6a = 15 / 2b = 10c a = 5c / 3 b = 4c / 3 Найдем полупериметр : (5с / 3 + 4с / 3 + c) / 2 = 2c По формуле Герона : S = sqrt(2c * c / 3 * 2c / 3 * c) = (2c ^ 2) / 3 Приравняем площади : 10с = (2c..

Источник

Волжский класс

Боковая колонка

Видео

Книжная полка

Малина для Админа

Боковая колонка

Опросы

Календарь

Декабрь 2021

Пн	Вт	Ср	Чт	Пт	Сб	Вс
1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30	31

7 класс. Геометрия. Атанасян. Учебник. Ответы к стр. 17

Начальные геометрические сведения
Измерение отрезков
Длина отрезка. Единицы измерения. Измерительные инструменты

Ответы к стр. 17

Задачи

30. Точка В делит отрезок АС на два отрезка. Найдите длину отрезка АС, если АВ = 7,8 см, ВС = 25 мм.

Р е ш е н и е
АС = АВ + ВС
ВС = 25 мм = 2,5 см
АС = 7,8 + 2,5 = 10,3 (см)

О т в е т. АС = 10,3 см.

31. Точка В делит отрезок АС на два отрезка. Найдите длину отрезка ВС, если: а) АВ = 3,7 см, АС = 7,2 см; б) AB = 4 мм, АС = 4 см.

О т в е т. ВС = 3,5 см.

О т в е т. ВС = 36 мм.

32. Точки А, B и С лежат на одной прямой. Известно, что AB = 12 см, BC = 13,5 см. Какой может быть длина отрезка АС?

Р е ш е н и е.
Рассмотрим взаимное расположение точек: А — В — С или В — А — С (А — С — В быть не может, так как по условию задачи АВ

О т в е т. Длина отрезка АС может быть 25,5 см или 1,5 см.

33. Точки B, D и М лежат на одной прямой. Известно, что BD = 7 см, MD = 16 см. Каким может быть расстояние BM?

Р е ш е н и е.
Рассмотрим взаимное расположение точек: В — D — М или D — В — М (В — М — D быть не может, так как по условию задачи ВD

О т в е т. Расстояние BM может быть 23 см или 9 см.

34. Точка С — середина отрезка AB, равного 64 см. На луче СА отмечена точка D так, что CD = 15 см. Найдите длины отрезков BD и DA.

Р е ш е н и е.
AC = BC = AB : 2 = 64 : 2 = 32 (см)
АС = 32 см, СD = 15 см ⇒ АС > СD и расположение точек будет: A — D — C — B
АС = АD + СD ⇒ DA = AC — CD = 32 — 15 = 17 (см)
АВ = АD + DB ⇒ BD = AB — DА = 64 — 17 = 47 (см) или
BD = CD + BC = 15 + 32 = 47 (см)

О т в е т. Длина отрезка BD = 47 см, отрезка DA = 17 см.

35. Расстояние между Москвой и С.-Петербургом равно 650 км. Город Тверь находится между Москвой и С.-Петербургом в 170 км от Москвы. Найдите расстояние между Тверью и С.-Петербургом, считая, что все три города расположены на одной прямой.

Д а н о
Москва — С.-Петербург = 650 км
Москва — Тверь — С.-Петербург
Москва — Тверь = 170 км

Р е ш е н и е.
Москва — т. М, Тверь — т. Т, С.-Петербург — т. S
Расположение точек на прямой: М — Т — S
MS = MT + TS ⇒ TS = MS — MT = 650 — 170 = 480 (км)

О т в е т. Расстояние между Тверью и С.-Петербургом 480 км.

36. Лежат ли точки А, B и С на одной прямой, если АС = 5 см, AB = 3 см, BC = 4 см?

Р е ш е н и е.
Если точки А, В и С лежат на одной прямой, то больший из отрезков АВ, ВС и АС равен сумме двух других. По условию больший из из данных отрезков (отрезок АС) равен 5 см, а сумма двух других (АВ + ВС) равна 7 см. Поэтому точки А, В и С не лежат на одной прямой.

О т в е т. А, В и С не лежат на одной прямой.

37. Точка С — середина отрезка AB, точка О — середина отрезка АС. Найдите:
а) АС, СB, АО и ОB, если AB = 2 см;
б) AB, АС, АО и ОB, если СB = 3,2 м.

Р е ш е н и е
а) Расположение точек: А — О — С — В
AC = CВ = AB : 2 = 2 : 2 = 1 (см)
АО = ОС = АС : 2 = 1 : 2 = 0,5 (см)
ОВ = ОС + СВ = 0,5 + 1 = 1,5 (см)

О т в е т. АС = 1 см, СB = 1 см, АО = 0,5 см, ОB = 1,5 см.

б) Расположение точек: А — О — С — В
СВ = АВ : 2 ⇒ АВ = 2СВ = 2 • 3,2 = 6,4 (м)
АС = CB = 3,2 м
АО = ОС = АС : 2 = 3,2 : 2 = 1,6 (м)
ОВ = ОС + СВ = 1,6 + 3,2 = 4,8 (м)

О т в е т. АВ = 6,4 см, АС = 3,2 см, АО = 1,6 см, ОB = 4,8.

38. На прямой отмечены точки О, А и B так, что ОА = 12 см, ОB = 9 см. Найдите расстояние между серединами отрезков ОА и ОB, если точка О:
а) лежит на отрезке AB;
б) не лежит на отрезке AB.

Н а й т и
Расстояние между серединами ОА и ОВ, если:
а) О ∈ АВ;
б) О ∉ АВ.

Р е ш е н и е
а) Расположение точек: А — О — В
Дополнительные построения: т. С — середина ОА, т. Е — середина ОВ

АС = СО = АО : 2 = 12 : 2 = 6 (см)
ВЕ = ЕО = ВО : 2 = 9 : 2 = 4,5 (см)
Тогда: А — С — О — Е — В, расстояние между серединами ОА и ОВ — отрезок СЕ.
СЕ = СО + ОЕ = 6 + 4,5 = 10,5 (см)

О т в е т. Расстояние между серединами ОА и ОВ 10,5 см.

б) Расположение точек: О — В — А (О — А — В быть не может, так как по условию задачи ОА > ОВ).
Дополнительные построения: т. С — середина ОА, т. Е — середина ОВ

АС = СО = АО : 2 = 12 : 2 = 6 (см)
ВЕ = ЕО = ВО : 2 = 9 : 2 = 4,5 (см)
Так как СО > ЕО, то Е ∈ СО
Тогда: О — В — С — Е — А, расстояние между серединами ОА и ОВ — отрезок СЕ.
СО = СЕ + ЕО ⇒ СЕ = СО — ЕО = 6 — 4,5 = 1,5 (см)

О т в е т. Расстояние между серединами ОА и ОВ 1,5 см.

39. Отрезок, длина которого равна α, разделен произвольной точкой на два отрезка. Найдите расстояние между серединами этих отрезков.

Р е ш е н и е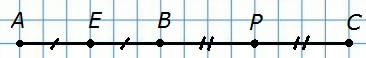

Расположение точек: А — Е — В — Р — С
АЕ = ЕВ = 1 /₂ АB
ВР = РС = 1 /₂ ВС
ЕР = ЕВ + ВР = 1 /₂ АВ + 1 /₂ ВС = 1 /₂ (АВ + ВС) = 1 /₂ АС = 1 /₂ α

40. Отрезок, равный 28 см, разделён на три неравных отрезка. Расстояние между серединами крайних отрезков 16 см. Найдите длину среднего отрезка.

Р е ш е н и е

Расположение точек: А — Р — С — Е — М — В
АР + МВ = АВ — РМ = 28 — 16 = 12 (см)
АР = РС, МВ = ЕМ ⇒ АР + МВ = РС + ЕМ
АР + МВ + РС + ЕМ = 12 + 12 = 24 (см)
СЕ = АВ — (АР + МВ + РС + ЕМ) = 28 — 24 = 4 (см)

Источник

Длина отрезка bc на рисунке равна известно что точка м середина отрезка

Площадь треугольника АВС равна 12. На прямой АС взята точка D так, что точка С является серединой отрезка AD. Точка K — середина стороны AB, прямая KD пересекает сторону BC в точке L.

a) Докажите, что BL : LC = 2 : 1.

б) Найдите площадь треугольника BLK.

а) Соединим отрезками точки B и D, A и L. Рассмотрим треугольник АВD. Ясно, что L — точка пересечения медиан этого треугольника. Отсюда BL : LC = 2 : 1, что и требовалось доказать.

б) Как известно, медианы треугольника, пересекаясь в одной точке, делят его на 6 равновеликих треугольников. Учитывая то, что L — точка пересечения медиан а также получим:

Точка D делит сторону AC в отношении AD : DC = 1 : 2.

а) Докажите, что в треугольнике ABD найдётся медиана, равная одной из медиан треугольника DBC.

б) Найдите длину этой медианы в случае, если AB = 7, BC = 8, и AC = 9.

а) Обозначим середины отрезков BA, BD, BC за E, F, G соответственно. Тогда EG — средняя линия треугольника ABC, и точка F лежит на ней. Поскольку FG — средняя линия DBC, то Итак, в четырехугольнике AFGD две стороны равны и параллельны, значит, он параллелограмм и

б) По теореме косинусов в треугольнике ABC имеем откуда

По теореме косинусов в треугольнике DGC имеем откуда

Ответ:

Площадь треугольника ABC равна 10; площадь треугольника AHB, где H — точка пересечения высот, равна 8. На прямой CH взята такая точка K, что треугольник ABK — прямоугольный.

а) Докажите, что

б) Найдите площадь треугольника ABK.

а) Заметим, что поскольку тогда или как перпендикуляры к одной прямой. Значит, Обозначим основания высот треугольника ABC за Тогда точки K, B, A, A₁, B₁ лежат на окружности с диаметром AB (из-за прямых углов). заметим, что — основание перпендикуляра из K на