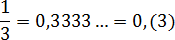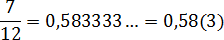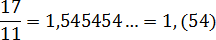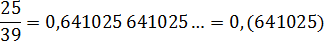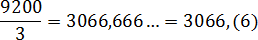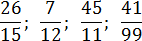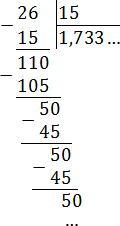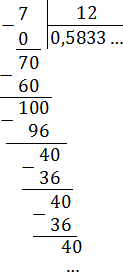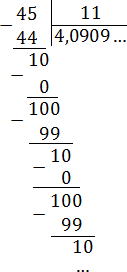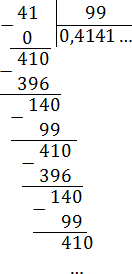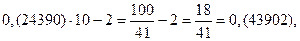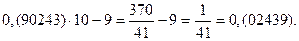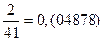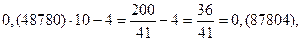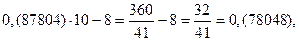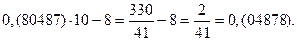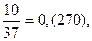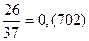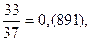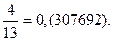Длина периода это что
Периодические десятичные дроби
Помните, как в самом первом уроке про десятичные дроби я говорил, что существуют числовые дроби, не представимые в виде десятичных (см. урок «Десятичные дроби»)? Мы еще учились раскладывать знаменатели дробей на множители, чтобы проверить, нет ли там чисел, отличных от 2 и 5.
Так вот: я наврал. И сегодня мы научимся переводить абсолютно любую числовую дробь в десятичную. Заодно познакомимся с целым классом дробей с бесконечной значащей частью.
— это любая десятичная дробь, у которой:
Поскольку определений много, стоит подробно рассмотреть несколько таких дробей:
Эта дробь встречается в задачах чаще всего. Непериодическая часть: 0; периодическая часть: 3; длина периода: 1.
Непериодическая часть: 0,58; периодическая часть: 3; длина периода: снова 1.
Непериодическая часть: 1; периодическая часть: 54; длина периода: 2.
Непериодическая часть: 0; периодическая часть: 641025; длина периода: 6. Для удобства повторяющиеся части отделены друг от друга пробелом — в настоящем решении так делать не обязательно.
Непериодическая часть: 3066; периодическая часть: 6; длина периода: 1.
Как видите, определение периодической дроби основано на понятии значащей части числа. Поэтому если вы забыли что это такое, рекомендую повторить — см. урок «Умножение и деление десятичных дробей».
Переход к периодической десятичной дроби
Рассмотрим обыкновенную дробь Разложим ее знаменатель на простые множители. Возможны два варианта:
Чтобы задать периодическую десятичную дробь, надо найти ее периодическую и непериодическую часть. Как? Переведите дробь в неправильную, а затем разделите числитель на знаменатель «уголком».
При этом будет происходить следующее:
Вот и все! Повторяющиеся цифры после десятичной точки обозначаем периодической частью, а то, что стоит спереди — непериодической.
Задача. Переведите обыкновенные дроби в периодические десятичные:
Все дроби без целой части, поэтому просто делим числитель на знаменатель «уголком»:
Как видим, остатки повторяются. Запишем дробь в «правильном» виде:
В итоге получается дробь:
Записываем в нормальном виде:
Переход от периодической десятичной дроби к обыкновенной
Рассмотрим периодическую десятичную дробь Требуется перевести ее в классическую «двухэтажную». Для этого выполним четыре простых шага:
Задача. Приведите к обыкновенной неправильной дроби числа:
Работаем с первой дробью:
В скобках содержится лишь одна цифра, поэтому период Далее умножаем эту дробь Имеем:
Вычитаем исходную дробь и решаем уравнение:
Теперь разберемся со второй дробью. Итак,
Период k = 2, поэтому умножаем все
Снова вычитаем исходную дробь и решаем уравнение:
100 X − X =
99 X = 3207;
X = 3207/99 = 1069/33.
Приступаем к третьей дроби: Схема та же самая, поэтому я просто приведу выкладки:
Период k = 1 ⇒ умножаем все на 10 k = 10 1 = 10;
Наконец, последняя дробь: Опять же, для удобства периодические части отделены друг от друга пробелами. Имеем:
Это очень просто
Рассмотрим следующую задачу. Найти период дроби 1/81. Уверяю, что для решения не потребуется ни калькулятор, ни деление столбиком. Для начала вспомним чему равно 81*(Период). Пусть длина периода n, тогда исходная дробь запишется как:
Перепишем данное представление в следующем виде:
Последнее выражение можно представить так:
Ну а теперь то соотношение, которое мы искали:
Для нашего случая это тождество будет следующим:
Разделим левую и правую часть на 9, получим:
Первое число, составленное из одних единиц, которое делится на 9 равно 111111111, это следует из признака делимости на 9. Делить будем через сумму цифр исходного числа. Двигаемся слева направо, складываем цифры делимого и на каждом шаге записываем полученную сумму. Результат работы данного алгоритма — число 12345678,9999… Здесь надо пояснить, что когда мы достигаем крайней правой цифры, то ставим запятую и полученную сумму цифр исходного числа дублируем как бесконечную десятичную дробь. Вспоминаем, что 0,999. =1 и получаем ответ, который мы искали 12345679. Если рассмотреть более общую задачу нахождения периода дроби , то окажется, что период такой дроби имеет длину
и если известен период для случая n-1, то следующий равен произведению данного периода на число вида 11111… (повторяется
раз)22222… (повторяется
раз)33333… (повторяется
раз). Самая правая секция будет иметь вид 8888..889. Последняя цифра девятка.
И еще одно наблюдение, теперь для дробей вида . В этом случае длина периода равна
. И если известен период для случая n-1, то следующий период равен произведению данного периода на число, составленное из 10 блоков, где длина каждого блока
. Блоки имеют следующую структуру:
09090909…
18181818…
27272727…
36363636…
…
последний блок 90909091. Для период 09, для
период будет 09182736455463728191*9=0082644628099173553719.
Проверил формулу для . Получил
75131480090157776108189331329827197595792637114951164537941397445529676934635612
32156273478587528174305033809166040570999248685199098422238918106686701728024042
0736288504883546205860255447032306536438767843726521412471825694966190833959429,
что совпадает с периодом без ведущих нулей.
Приведу код процедур, которые я использовал для проверки своих выводов.
Глава 2 Свойства периодических дробей
Великий немецкий математик Карл Фридрих Гаусс, будучи гимназистом, обращал дроби вида 1/р, где р – простое число, отличное от 2 и 5, в бесконечные десятичные дроби: в каждом случае он с поразительным терпением ожидал, когда знаки начнут повторяться. Ему хотелось понять, как зависит длина периода такой дроби от р.
Мы в своей работе для вычисления длины периода использовали программу, написанную на языке Паскаль.
И вот, что получилось.
р – знаменатель дроби (простое число, отличное от 2 и 5), L(p) – количество цифр в периоде.
Т.о. из таблицы видно, что длина L(p) наименьшего периода для некоторых дробей совпадает с числом р – 1. А именно, L(p) = р – 1 для р = 7, 17, 19, 23, 47, 59, 61, 97, 109, 113 и т.д.. Конечно или бесконечно множество таких чисел по сей день неизвестно.
Также из таблицы видна еще одна закономерность: длина наименьшего периода является делителем числа р – 1
Рассмотрим записи обыкновенных дробей в виде периодических
| Обыкновенная дробь | Периодическая дробь |
| 1/7 | 0,(124857) |
| 2/7 | 0,(285714) |
| 3/7 | 0,(428571) |
| 4/7 | 0,(571428) |
| 5/7 | 0,(714285) |
| 6/7 | 0,(857142) |
| Обыкновенная дробь | Периодическая дробь | Обыкновенная дробь | Периодическая дробь |
| 1/11 | 0,(09) | 6/11 | 0,(54) |
| 2/11 | 0,(18) | 7/11 | 0,(63) |
| 3/11 | 0,(27) | 8/11 | 0,(72) |
| 4/11 | 0,(36) | 9/11 | 0,(81) |
| 5/11 | 0,(45) | 10/11 | 0,(90) |
| Обыкновенная дробь | Периодическая дробь | Обыкновенная дробь | Периодическая дробь |
| 1/13 | 0,(076923) | 7/13 | 0,(538461) |
| 2/13 | 0,(153846) | 8/13 | 0,(615384) |
| 3/13 | 0,(230769) | 9/13 | 0,(692307) |
| 4/13 | 0,(307692) | 10/13 | 0,(769230) |
| 5/13 | 0,(384615) | 11/13 | 0,(615384) |
| 6/13 | 0,(461538) | 12/13 | 0,(923076) |
Удивительно, но какую бы дробь мы не взяли, сумма цифр периода кратна девяти:
для дробей со знаменателем 7 эта сумма равна 27 = 9 × 3;
для дробей со знаменателем 11: 9 = 9 × 1;
для дробей со знаменателем 13: 27 = 9 × 3;
для дробей со знаменателем 19: 81 = 9 × 9;
для дробей со знаменателем 31: 54 = 9 × 6;
для дробей со знаменателем 37: 9 = 9 × 1 или 18 = 9 × 2 и т. д.
Докажем это свойство. Рассмотрим дробь вида 
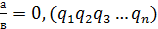
Из полученных равенств выразим q1, q2, q3 и т.д. и найдем сумму этих чисел. Получим:


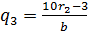
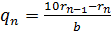
q1 + q2 + q3 + … + qn = 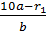

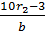

= 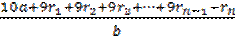
a = rn) = 
2.2 Циклические сдвиги
Рассмотрим следующие разложения:
Периоды этих шести дробей начинаются сразу же после запятой и получаются друг из друга циклическим сдвигом. Случайно ли это?
Возьмем вместо 7, например, 41.
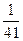
«Прокрутим» период: 0,(24390) = 
Полученная дробь в 10 раз больше первоначальной. Посмотрим, что получится, если мы полученную дробь снова умножим на 10 и вычтем целую часть.
Получился замкнутый цикл из дробей, имеющих одинаковые цифры в периоде. Проведем аналогичные операции, взяв другую дробь.
Снова получился замкнутый цикл из дробей с одинаковыми цифрами в периоде, причем, количество дробей в цикле одинаково.
Таким образом, можно предположить, что десятичные дроби образуют замкнутые циклы, в которые входят дроби, имеющие одинаковые цифры в периоде, причем каждую последующую дробь можно получить из предыдущей умножением на десять с последующим вычитанием целой части.
2.3 Особенности числителей дробей цикла
Рассмотрим некоторые циклы.

Заметим, что сумма числителей дробей равна знаменателю: 1 + 10 + 26 = 34.
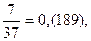
Заметим, что сумма числителей дробей равна удвоенному знаменателю: 7 + 33 + 34 = 74 = 37 × 2.
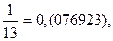
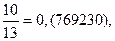
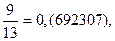
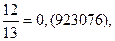
Заметим, что сумма числителей дробей равна утроенному знаменателю: 1 + 10 + 9 + 12 + 3 + 4 = 39 = 13 ×3.
Во всех случаях сумма числителей дробей, образующих цикл, кратна знаменателю. Проанализировав, полученные нами данные, мы заметили следующую закономерность: сумма числителей дробей цикла во столько раз больше знаменателя дроби, во сколько раз сумма цифр периода больше 9.
Дата добавления: 2014-11-30 ; просмотров: 2329 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Длина периода это что
Вероятно, читатель знает (а если нет ещё лучше: он узнает это из нашей статьи), что всякая обыкновенная дробь представляется периодической десятичной дробью (конечную десятичную дробь мы можем считать периодической с Но вряд ли многие представляют, сколько неожиданностей заключает в себе эта периодическая дробь. Рассмотрим три примера:
7
12
Мы видим, что у чисел 1 / 7 и 1 / 13 период начинается сразу после запятой и состоит из шести цифр (142857 и 076923 соответственно), а у он начинается с третьей позиции после запятой и состоит из единственной Внимательное рассмотрение периодов позволяет заметить ещё одно обстоятельство. Именно, положим (период и будем последовательно умножать
| 2 N = 285714, | 3 N = 428571, |
| 4 N = 571428, | 5 N = 714285, |
| 6 N = 857142, | 7 N = 999999. |
Мы видим, что первые пять из этих чисел получаются из числа N «круговой перестановкой» цифр: цифр из конца числа переезжает в начало; а состоит из одних девяток. Теперь проделаем то же с периодом
| 2 N = 153846, | 3 N = 230769, |
| 4 N = 307692, | 5 N = 384615, |
| 6 N = 461538, | 7 N = 538461, |
| 8 N = 615384, | 9 N = 692307, |
| 10 N = 769230, | 11 N = 846153, |
| 12 N = 923076, | 13 N = 999999. |
Можно заметить ещё вот что. Если взять любое из выписанных выше шестизначных чисел, кроме числа 999999, «разломить» его на два трёхзначных числа и вычислить сумму этих половинок, то получится 999; например,
Как видите, с периодическими десятичными дробями связано немало загадок. Некоторые из этих загадок остаются не разгаданными по сей день, несмотря на многочисленные попытки, предпринимавшиеся на протяжении нескольких веков математиками из разных стран, как великими, так и более «скромными». Всё же об этом мы можем рассказать.
Хобби Иоганна Бернулли
Оставим на время периоды и перенесёмся в Швейцарию конца XVIII века. Мы наблюдаем странную картину: маститый математик Иоганн III Бернулли, представитель знаменитой математической семьи Бернулли, удостоившейся, подобно королевским династиям, присоединения порядковых номеров к именам, занимается, можно сказать, детской игрой! Он разлагает на простые множители числа, записываемые одними единицами: 11 = 11, В 1773 году Бернулли помещает в трудах Берлинской академии таблицу простых делителей чисел, составленных из до Несмотря на то, что ему не удалось найти делители для некоторых чисел этого вида 17, 29), а для трёх чисел 25, 27) разложение не доведено до простых множителей, несмотря на допущенные им ошибки (для 24, 26), мы сегодня можем только преклоняться перед гигантским трудом по вычислению простых множителей этих огромных чисел. Можно предположить, что автором таблицы двигала не только исследовательская жилка учёного, но и подлинная эстетическая страсть художника, вдохновлённого удивительным притягательным миром этой загадочной вереницы единиц. Свои сомнения в правильности разложения в отдельных случаях И. Бернулли отражает звёздочкой.

Рис. 1.
В течение первых ста лет, прошедших со времени опубликования таблицы И. Бернулли, в неё не было внесено особой ясности. В 1838 году Вестерберг разложил на простые множители число из и это всё. В 1879 году французский математик Эдуард Люка находит простые делители для и признаёт, что цепочка из не поддаётся разложению. В 1895 году в Париже выходит его книга «Занимательная арифметика», содержащая приведённую ниже таблицу.
| ||||||||||||||||||||||||||||||||||
Угасший было интерес к числам, составленным из единиц, вновь возрос в последние годы, особенно в связи с развитием теории арифметических кодов, служащей основой для реализации методов помехоустойчивого кодирования в компьютерной технике (см., например, книгу Ю. Г. Дадаева «Теория арифметических кодов», изданную в Москве в 1981 г.). Наши загадочные числа, спустя почти двести лет после опубликования первой таблицы их делителей, приобретают, наконец, собственное имя. В «Занимательной теории чисел» 1964 г.) её автор А. Бейлер, посвятив этим числам целую главу под названием «111. 1111», вводит для них термин «repunit» (сокращение английского repeated unit повторенная единица). Русского слова «репьюнит» ещё не найти в словарях, но оно уже появляется в рефератах к зарубежным статьям, приобретая силу нового международного термина.
Математики продолжают штурмовать таблицу делителей репьюнитов, и к n в таблице уже достигает 3000 (С. Ейтс), однако в ней ещё достаточно много пробелов. (К настоящему времени часть этих пробелов ликвидирована и найдены делители. репьюнитов включительно). Отдельный интерес представляют простые репьюниты, поиск которых также продолжается. Уже доказано, что и репьюниты простые.
Нас, однако, репьюниты интересуют не сами по себе, а в связи с периодами десятичных дробей. Существование связи между теми и другими предвидел и Бернулли, который одновременно с уже упоминавшейся таблицей делителей репьюнитов опубликовал обзор известных к тому времени результатов о периодах десятичных дробей, включавший в себя пространную таблицу этих периодов В действительности, эта связь, как мы сейчас увидим, лежит на поверхности.

Рис. 2.
Делители репьюнитов и
представление обыкновенных дробей десятичными
Начнём с трёх простых наблюдений.
( где несколько первых цифр a i могут быть нулями ). Тогда
Теперь мы можем сформулировать Важный Результат.
Всё это нами уже доказано. Между прочим, из этой теоремы вытекает следующий, довольно неожиданный результат.
Действительно, если m не делится на 3, то число делится на 9.
Утверждения о периодах в случаях, не охватываемых мы приведём в качестве упражнений.
Доказательство этого утверждения опирается на лемму: если р и q взаимно просты, то найдутся целые положительные A и B такие, что
Наконец, можно усилить наше следствие.
Теперь мы приступаем к изучению зависимости длин периодов от знаменателей. В этом изучении нам поможет, наряду с теоремой 1,
Малая теорема Ферма
В отличие от своей «Великой теоремы» малую теорему Пьер Ферма снабдил доказательством: он изложил его в в одном из писем. Теорема формулируется так:
Мы не приводим доказательства этой теоремы (хотя читатель, который проделает все упражнения к этой статье, вероятно сможет её доказать). Её доказательство имеется в популярной литературе (см., например, книгу Р. Куранта и Г. Роббинса «Что такое математика?», переизданную в Москве в 1976 г.). Нас эта теорема интересует, главным образом, как средство доказательства фундаментального свойства периодов.
Длина периода дроби с простым знаменателем
| | 999. 999 999. 999 999. 999 000. 000 |
| 999. 999 |
Это число составлено из p 1 n девяток, и оно тоже делится Проделав ещё одно подобное вычитание, мы находим, что делится число, составленное из девяток, потом из девяток В конце концов мы придём к числу, в котором девяток меньше, и тут есть две возможности. Либо это число вообще будет нулём, но это как раз и значит, что делится Либо в этом числе девяток будет но а это противоречит тому, что n наименьшая возможная длина числа из девяток, которое делится Теорема доказана.
Обозначим для числа m через L ( m ) длину периода десятичной дроби, Мы доказали, что если p простое число, то есть делитель числа Но какой? Посмотрим на таблицу И. Бернулли (рис. 2). Мы видим, что Ясности не много.
Кропотливая работа математиков по выявлению какой-нибудь закономерности в расположении этих групп среди всех простых чисел увенчалась неожиданным результатом. Было обнаружено достаточно устойчивое отношение численностей этих групп в пропорции при этом были использованы таблицы длин периодов для простых знаменателей до 1 370 471 включительно (С. Ейтс, 1975 г.). Были получены и другие общие результаты, причём оказалось, что большое значение при определении длины периода с имеет остаток от деления Например, если этот остаток 27, 31, 39, то нечётно, а если то чётно. Всё же задача вычисления чисел для видимо, далека от решения.
Случай непростого знаменателя
Поскольку всякое натуральное число есть произведение степеней простых, которые между собой взаимно просты, последнее утверждение сводит задачу вычисления длины периода к случаю, когда знаменатель есть степень простого числа. А здесь снова нет ясности: например,
Теперь нам пора оставить длины периодов и обратиться к объяснению феноменов, обнаруженных в начале статьи.
Эффект круговой перестановки
Напомним, в чём он состоит. Мы видели, что шестизначный период при умножении 3, 4, подвергается круговой перестановке: цифр из конца числа переезжает в начало. Несколько иначе ведёт себя при умножении на различные числа шестизначный период Впрочем, что именно с ним происходит, читатель может вспомнить, заглянув в начало статьи, а мы сейчас докажем теорему, более или менее объясняющую это явление.
Это периодическая десятичная дробь, период которой получается из периода круговой перестановкой цифр: переезжает из начала в конец; но в то же время это число больше а значит, и его период больше периода Теорема доказана.
Если число 1/ m имеет ( m 1 )-значный период, то доказанная теорема всё объясняет. Действительно, круговыми перестановками цифр из периода можно получить чисел (включая его самого), и все эти числа различны. С другой стороны, умножая период мы тоже получаем чисел; значит, это в точности те же числа. Если же период короче, то круговые перестановки цифр не исчерпывают всех чисел с Всё, что можно сказать в этом случае это что круговая перестановка цифр всегда приводит к числу это доказывается точно так же, как теорема 3.
Интересно, что теорема 3 в некотором смысле обращается:
что нам и требуется.
Сами того не желая, мы научились решать один тип олимпиадных задач. Вот пример.
Ответ : 102564, 128205, 142857, 153846, 179487, 205128, 230769.
Заметим, что простота q использовалась нами только в одном месте: мы вывели из неё, что взаимно просто Разумеется, эта взаимная простота может наступить и при так что заключение нашей теоремы справедливо и при многих непростых знаменателях.
Рассмотрим снова период дроби 1 / 7 : N = 142857. Возведём его в квадрат отделим последние шесть цифр и сложим с тем, что останется:
122449 + 20408 = 142857.
Получился снова наш период. Проделаем подобное с периодом
Получился, правда, не наш исходный период, но число, отличающееся от него на круговую перестановку цифр. Аналогичное для периода