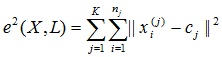Для чего используется кластеризация

Что такое кластеризация или кластерный анализ

Примеры кластеризации в маркетинге.

Если у вас есть большой массив данных, то наиболее эффективный способ понять, что с ними делать — рассортировать их в группы для первичного анализа. Группировать можно при помощи — сегментации (вы сами задаете критерии, например, возрастные и ценовые группы) или кластеризации (математический алгоритм сам выявляет “связующий” критерий или признак, который объединяет данные). Ценность data-driven подхода и основное отличие кластеризации заключается в том, что алгоритмы выявляют и объединяют параметры с похожими чертами из первичного массива данных.

Маркетинг и продажи — одно из направлений применения кластерного анализа. В частности для прогнозирования будущего поведения покупателя — персонализации и таргетирования. Кластерный анализ использует математические модели для обнаружения групп схожих клиентов, основываясь на наименьших различиях среди покупателей в каждой группе.

Кластерный анализ (англ. cluster analysis) — многомерная статистическая процедура, выполняющая сбор данных, содержащих информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы.

Боль: кампании, как маркетинговая инвестиция, должны быть направлены на конкретную целевую группу.

Стандартный пул данных в датасете:

Более глубокое понимание клиентских сегментов достигается путем разработки 3D-модели кластеров на основе ключевых бизнес-показателей, таких как размещенные заказы (покупки), частота заказов, заказанные товары или изменение цен. Актуальность результатов кластеризации для бизнеса позволяет лицам, принимающим решения, выявлять проблемные кластеры, которые вынуждают продавца использовать больше ресурсов для достижения целевого результата. Затем можно сосредоточить свои маркетинговые и операционные усилия на правильных кластерах, чтобы обеспечить оптимальное использование ресурсов, включая:

Хотя возможности прогнозирования, предлагаемые кластеризацией, могут трансформировать результаты целевого маркетинга, кластеризация наиболее эффективна при использовании вместе с другими решениями для розничной аналитики. Ценность кластеризации продуктов особенно видна в очень разреженном датасете (наборе данных). В дополнение к повышению рентабельности маркетинговых инвестиций (ROMI) с точки зрения прибыльности клиентов, кластеризация продуктов может помочь ритейлерам таргетировать и активизировать клиентов из категории с невысокой платежеспособностью.

Подробнее о функционале модуля “Кластеризация” смотрите в обучающем видео.

Источник

Кластеризация

Кластеризация — это разбиение множества объектов на подмножества (кластеры) по заданному критерию. Каждый кластер включает максимально схожие между собой объекты. Представим переезд: нужно разложить по коробкам вещи по категориям (кластерам) — например одежда, посуда, декор, канцелярия, книги. Так удобнее перевозить и раскладывать предметы в новом жилье. Процесс сбора вещей по коробкам и будет кластеризацией.

Критерии кластеризации определяет человек, а не алгоритм, — этим она отличается от классификации. Этот метод машинного обучения (Machine Learning) часто применяют в различных неструктурированных данных — например если нужно автоматически разбить коллекцию изображений на мини-группы по цветам.

Кластерный анализ применяют в разных сферах:

Типы входных данных

Признаковое описание объектов

Объект описывается при помощи набора характеристик. Признаки бывают числовые и категориальные. Например, можно кластеризовать группу покупателей на основе их покупок в интернет-магазине. В качестве входных данных будут средний чек, возраст, количество покупок в месяц, любимая категория покупок и другие критерии.

Матрица расстояний между выделенными объектами

Это симметричная таблица, где по строкам и столбцам расположены объекты, а на пересечении — расстояние между ними: например, таблица с расстояниями между отелями в разных городах. Такой способ может помочь выделить кластеры отелей, которые сгруппированы в одной и той же локации.

Освойте самую востребованную технологию искусственного интеллекта. Дополнительная скидка 5% по промокоду BLOG.

Цели кластеризации

Сжатие данных

Кластеризация актуальна, если исходная выборка слишком большая. В результате от каждого кластера остается по одному типичному представителю. Количество кластеров может быть любым — здесь важно обеспечить максимальное сходство объектов внутри каждой группы.

Поиск паттернов внутри данных

Разбиение объектов на кластеры позволяет добавить дополнительный признак каждому объекту. Так, если в результате кластерного анализа выявилось, что определенный покупатель относится к первому кластеру, и мы знаем, что первый кластер — это кластер людей, которые тратят большое количество денег на покупки по средам, то можно сказать, что это покупатель приобретает продукты в основном по средам.

Поиск аномалий

В этом случае выделяют нетипичные объекты, не подходящие ни к одному сформированному кластеру. Интересны отдельные объекты, которые не вписываются ни в одну из сформированных групп.

Методы кластеризации

Общепринятой классификации методов нет, но есть несколько групп подходов.

1. Вероятностный подход. В рамках него предполагается, что каждый из объектов относится к одному из классов.

2. Подходы с учетом систем искусственного интеллекта. Большая условная группа методов, разнится с методической точки зрения.

4. Иерархический подход. Предполагает наличие вложенных групп — кластеров разного порядка. Выделяются агломеративные и дивизионные (объединительные и разделяющие) алгоритмы. В зависимости от количества признаков могут выделяться политетические (используют при сравнении нескольких признаков одновременно) и монотетические (используют при применении одного признака) методы классификации.

Как описать кластеризацию формально?

В кластеризации имеют дело с множеством объектов (X) и множеством номеров кластеров (Y). Задана функция расстояния между объектами ( p). Нужно разбить обучающую выборку на кластеры, так чтобы каждый кластер состоял из объектов, близких по метрике p, а объекты разных кластеров существенно отличались. При этом каждому объекту приписывается номер кластера y(i).

Алгоритм кластеризации — это функция, которая любому объекту X ставит в соответствие номер кластера Y.

Data Science с нуля

Вы получите достаточную математическую подготовку и опыт программирования на Python, чтобы решать задачи машинного обучения.

Источник

Кластеризация

Материал из MachineLearning.

Кластерный анализ (Data clustering) — задача разбиения заданной выборки объектов (ситуаций) на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались.

Задача кластеризации относится к широкому классу задач обучения без учителя.

Содержание

Типология задач кластеризации

Типы входных данных

Матрица расстояний может быть вычислена по матрице признаковых описаний объектов бесконечным числом способов, в зависимости от того, как ввести функцию расстояния (метрику) между признаковыми описаниями. Часто используется евклидова метрика, однако этот выбор в большинстве случаев является эвристикой и обусловлен лишь соображениями удобства.

Обратная задача — восстановление признаковых описаний по матрице попарных расстояний между объектами — в общем случае не имеет решения, а приближённое решение не единственно и может иметь существенную погрешность. Эта задача решается методами многомерного шкалирования.

Таким образом, постановка задачи кластеризации по матрице расстояний является более общей. С другой стороны, при наличии признаковых описаний часто удаётся строить более эффективные методы кластеризации.

Цели кластеризации

В первом случае число кластеров стараются сделать поменьше. Во втором случае важнее обеспечить высокую (или фиксированную) степень сходства объектов внутри каждого кластера, а кластеров может быть сколько угодно. В третьем случае наибольший интерес представляют отдельные объекты, не вписывающиеся ни в один из кластеров.

Во всех этих случаях может применяться иерархическая кластеризация, когда крупные кластеры дробятся на более мелкие, те в свою очередь дробятся ещё мельче, и т. д. Такие задачи называются задачами таксономии.

Результатом таксономии является древообразная иерархическая структура. При этом каждый объект характеризуется перечислением всех кластеров, которым он принадлежит, обычно от крупного к мелкому. Визуально таксономия представляется в виде графика, называемого дендрограммой.

Классическим примером таксономии на основе сходства является биноминальная номенклатура живых существ, предложенная Карлом Линнеем в середине XVIII века. Аналогичные систематизации строятся во многих областях знания, чтобы упорядочить информацию о большом количестве объектов.

Функции расстояния

Методы кластеризации

Формальная постановка задачи кластеризации

Решение задачи кластеризации принципиально неоднозначно, и тому есть несколько причин:

Источник

Обзор алгоритмов кластеризации данных

В своей дипломной работе я проводил обзор и сравнительный анализ алгоритмов кластеризации данных. Подумал, что уже собранный и проработанный материал может оказаться кому-то интересен и полезен.
О том, что такое кластеризация, рассказал sashaeve в статье «Кластеризация: алгоритмы k-means и c-means». Я частично повторю слова Александра, частично дополню. Также в конце этой статьи интересующиеся могут почитать материалы по ссылкам в списке литературы.

Так же я постарался привести сухой «дипломный» стиль изложения к более публицистическому.

Понятие кластеризации

Кластеризация (или кластерный анализ) — это задача разбиения множества объектов на группы, называемые кластерами. Внутри каждой группы должны оказаться «похожие» объекты, а объекты разных группы должны быть как можно более отличны. Главное отличие кластеризации от классификации состоит в том, что перечень групп четко не задан и определяется в процессе работы алгоритма.

Меры расстояний

Итак, как же определять «похожесть» объектов? Для начала нужно составить вектор характеристик для каждого объекта — как правило, это набор числовых значений, например, рост-вес человека. Однако существуют также алгоритмы, работающие с качественными (т.н. категорийными) характеристиками.

Классификация алгоритмов

Объединение кластеров

Обзор алгоритмов

Алгоритмы иерархической кластеризации

Среди алгоритмов иерархической кластеризации выделяются два основных типа: восходящие и нисходящие алгоритмы. Нисходящие алгоритмы работают по принципу «сверху-вниз»: в начале все объекты помещаются в один кластер, который затем разбивается на все более мелкие кластеры. Более распространены восходящие алгоритмы, которые в начале работы помещают каждый объект в отдельный кластер, а затем объединяют кластеры во все более крупные, пока все объекты выборки не будут содержаться в одном кластере. Таким образом строится система вложенных разбиений. Результаты таких алгоритмов обычно представляют в виде дерева – дендрограммы. Классический пример такого дерева – классификация животных и растений.

Для вычисления расстояний между кластерами чаще все пользуются двумя расстояниями: одиночной связью или полной связью (см. обзор мер расстояний между кластерами).

К недостатку иерархических алгоритмов можно отнести систему полных разбиений, которая может являться излишней в контексте решаемой задачи.

Алгоритмы квадратичной ошибки

Задачу кластеризации можно рассматривать как построение оптимального разбиения объектов на группы. При этом оптимальность может быть определена как требование минимизации среднеквадратической ошибки разбиения:

где c_j — «центр масс» кластера j (точка со средними значениями характеристик для данного кластера).

К недостаткам данного алгоритма можно отнести необходимость задавать количество кластеров для разбиения.

Нечеткие алгоритмы

Алгоритмы, основанные на теории графов

Суть таких алгоритмов заключается в том, что выборка объектов представляется в виде графа G=(V, E), вершинам которого соответствуют объекты, а ребра имеют вес, равный «расстоянию» между объектами. Достоинством графовых алгоритмов кластеризации являются наглядность, относительная простота реализации и возможность вносения различных усовершенствований, основанные на геометрических соображениях. Основными алгоритмам являются алгоритм выделения связных компонент, алгоритм построения минимального покрывающего (остовного) дерева и алгоритм послойной кластеризации.

Алгоритм выделения связных компонент

В алгоритме выделения связных компонент задается входной параметр R и в графе удаляются все ребра, для которых «расстояния» больше R. Соединенными остаются только наиболее близкие пары объектов. Смысл алгоритма заключается в том, чтобы подобрать такое значение R, лежащее в диапазон всех «расстояний», при котором граф «развалится» на несколько связных компонент. Полученные компоненты и есть кластеры.

Для подбора параметра R обычно строится гистограмма распределений попарных расстояний. В задачах с хорошо выраженной кластерной структурой данных на гистограмме будет два пика – один соответствует внутрикластерным расстояниям, второй – межкластерным расстояния. Параметр R подбирается из зоны минимума между этими пиками. При этом управлять количеством кластеров при помощи порога расстояния довольно затруднительно.

Алгоритм минимального покрывающего дерева

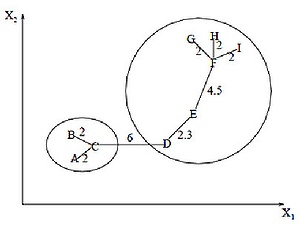
Алгоритм минимального покрывающего дерева сначала строит на графе минимальное покрывающее дерево, а затем последовательно удаляет ребра с наибольшим весом. На рисунке изображено минимальное покрывающее дерево, полученное для девяти объектов.

Путём удаления связи, помеченной CD, с длиной равной 6 единицам (ребро с максимальным расстоянием), получаем два кластера: и . Второй кластер в дальнейшем может быть разделён ещё на два кластера путём удаления ребра EF, которое имеет длину, равную 4,5 единицам.

Послойная кластеризация

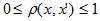
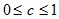
Алгоритм послойной кластеризации основан на выделении связных компонент графа на некотором уровне расстояний между объектами (вершинами). Уровень расстояния задается порогом расстояния c. Например, если расстояние между объектами , то .

Алгоритм послойной кластеризации формирует последовательность подграфов графа G, которые отражают иерархические связи между кластерами:

,

Источник

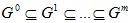
Национальная библиотека им. Н. Э. Баумана
Bauman National Library

Персональные инструменты

Кластерный анализ

Кластерный анализ (англ. cluster analysis) — многомерная статистическая процедура, выполняющая сбор данных, содержащих информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы.

Содержание

Введение

Историческая справка

Первое применение кластерный анализ нашел в социологии. Название кластерный анализ происходит от английского слова cluster – гроздь, скопление. Впервые в 1939 был определен предмет кластерного анализа и сделано его описание исследователем Трионом (Tryon). Главное назначение кластерного анализа – разбиение множества исследуемых объектов и признаков на однородные в соответствующем понимании группы или кластеры. Это означает, что решается задача классификации данных и выявления соответствующей структуры в ней. Методы кластерного анализа можно применять в самых различных случаях, даже в тех случаях, когда речь идет о простой группировке, в которой все сводится к образованию групп по количественному сходству.

Достоинства

Большое достоинство кластерного анализа в том, что он позволяет производить разбиение объектов не по одному параметру, а по целому набору признаков. Кроме того, кластерный анализ в отличие от большинства математико-статистических методов не накладывает никаких ограничений на вид рассматриваемых объектов, и позволяет рассматривать множество исходных данных практически произвольной природы. Это имеет большое значение, например, для прогнозирования конъюнктуры, когда показатели имеют разнообразный вид, затрудняющий применение традиционных эконометрических подходов. Кластерный анализ позволяет рассматривать достаточно большой объем информации и резко сокращать, сжимать большие массивы социально-экономической информации, делать их компактными и наглядными.

Важное значение кластерный анализ имеет применительно к совокупностям временных рядов, характеризующих экономическое развитие (например, общехозяйственной и товарной конъюнктуры). Здесь можно выделять периоды, когда значения соответствующих показателей были достаточно близкими, а также определять группы временных рядов, динамика которых наиболее схожа.

Кластерный анализ можно использовать циклически. В этом случае исследование производится до тех пор, пока не будут достигнуты необходимые результаты. При этом каждый цикл здесь может давать информацию, которая способна сильно изменить направленность и подходы дальнейшего применения кластерного анализа. Этот процесс можно представить системой с обратной связью. В задачах социально-экономического прогнозирования весьма перспективно сочетание кластерного анализа с другими количественными методами (например, с регрессионным анализом).

Недостатки

Как и любой другой метод, кластерный анализ имеет определенные недостатки и ограничения: в частности, состав и количество кластеров зависит от выбираемых критериев разбиения. При сведении исходного массива данных к более компактному виду могут возникать определенные искажения, а также могут теряться индивидуальные черты отдельных объектов за счет замены их характеристиками обобщенных значений параметров кластера. При проведении классификации объектов игнорируется очень часто возможность отсутствия в рассматриваемой совокупности каких-либо значений кластеров.

Задачи и решения

В кластерном анализе считается, что:

Выбор масштаба играет большую роль. Как правило, данные нормализуют вычитанием среднего и делением на стандартное отклонение, так что дисперсия оказывается равной единице.

Задача кластерного анализа

Решение задачи кластерного анализа

Решением задачи кластерного анализа являются разбиения, удовлетворяющие некоторому критерию оптимальности. Этот критерий может представлять собой некоторый функционал, выражающий уровни желательности различных разбиений и группировок, который называют целевой функцией. Например, в качестве целевой функции может быть взята внутригрупповая сумма квадратов отклонения:

Математические характеристики кластера

Неоднозначность задачи кластерного анализа

Стандартизация

Стандартизация (standardization) или нормирование (normalization) приводит значения всех преобразованных переменных к единому диапазону значений путем выражения через отношение этих значений к некой величине, отражающей определенные свойства конкретного признака. Существуют различные способы нормирования исходных данных:

Формальное описание задач кластеризации

Дано множество объектов данных I, каждый из которых представлен набором атрибутов. Требуется построить множество кластеров C и отображение F множества I на множество C, т.е. F: I → C. Отображение F задает модель данных, являющуюся решением задачи. Множество I определим следующим образом:

Задача кластеризации состоит в построении множества:

Расстояние

Алгоритмы (общее)

Решение задачи кластеризации принципиально неоднозначно, и тому есть несколько причин:

Меры близости

Существует четыре вида мер близости: меры расстояния, меры сходства, меры предсказуемости вероятностные коэффициенты сходства. Каждый из этих видов имеет свои достоинства и недостатки, которые следует рассматривать прежде, чем будет принято решение использовать какие-либо из них. Когда необходимо установить сходство между объектами, описываемыми бинарными переменными, применяются коэффициенты ассоциативности. Удобнее рассматривать эти коэффициенты, обратившись к таблице ассоциативности, в которой связь между объектами представлена в виде наличия и отсутствия признаков.

Меры расстояния

Меры сходства

Простой коэффициент совстречаемости имеет вид

Коэффициент Жаккара, определенный следующим образом

не учитывает одновременного отсутствия признака при вычислении сходства (клетка не d рассматривается). Он изменяется от 0 до 1. В противоположность коэффициенту совстречаимости коэффициент Жаккара принимает в расчет лишь те признаки, которые характерны хотя бы для одного из объектов.

Мера сходства Рассела и Рао, определенная как бинарное скалярное произведение, вычисляется по формуле:

Мера сходства Дайса:

Мера сходства Снита и Сокала (1):

Мера сходства Снита и Сокала (2):

Мера сходства Снита и Сокала (3):

Мера сходства Роджерса и Танимато:

Мера сходства Кулсински (1):

Вероятностные меры сходства

Вероятностные меры пригодны лишь для бинарных данных.

Мера сходства Кулсински (2), принимающая значения от 0 до 1, вычисляется как:

Мера сходства Снита и Сокала (4), принимающая значения от 0 до 1, определяется по формуле:

Мера сходства Хаманна, определенная на интервал [-1; +1], имеет вид:

Меры предсказуемости

Коэффициент Лямбда Гудмана и Крускала дает оценку предсказуемости состояния характеристик на один объект (наличие или отсутствие) заданного состояния на другой объект. Лямбда изменяется от 0 до 1 и вычисляется по формуле:

Коэффициент D Андерберга вычисляет уменьшение ошибки подобия, когда один объект применяется для прогнозирования другого объекта. D изменяется от 0 до 1 и определяется как:

Этот коэффициент равен нулю, если признаки независимы и может принимать значение +1, только когда bc = 0, т.е. в случае полной связности, а значение −1, только когда ad = 0, т.е. в случае полной отрицательной связности.

Другие бинарные меры

Мера сходства Снита и Сокала (5):

Корреляция четырех точек (аналог коэффициента Пирсона):

Дисперсия меры сходства:

Измерение близости объектов

Проблема измерения близости объектов неизбежно возникает при любых трактовках кластеров и различных методах классификации.

Отметим основные трудности, возникающие при этом: неоднозначность выбора способа нормировки и определения расстояния между объектами. Рассмотрим результаты небольшого обследования. Студенты группы записывают свои данные (вес, рост), оформляют в таблицу и строят по ним корреляционное поле. Масштабы по осям выбираются произвольно (рис.1.1).

На рис.1.1а выделяются классы A – девушки, B – юноши. На рис. 1.1b выделяются классы A1 (юноши и девушки) и B1(часть юношей). Класс юношей C (пунктирная линия) на рис. 1.1б не выделит, поскольку расстояния между ближайшими объектами классов A1 и B1 существенно больше, чем внутренние расстояния в A1, юноши из A почти никакими алгоритмами к B1 не присоединяются.

Однако определить расстояние между объектами в данном случае нельзя, поскольку признаки измерены в разных единицах измерения. Требуется нормировка показателей, переводящая их в безразмерные величины: тогда измерение близости объектов становится оправданным.

В кластерном анализе для количественной оценки сходства вводится понятие метрики. Сходство или различие между классифицируемыми объектами устанавливается в зависимости от метрического расстояния между ними. Если каждый объект описывается k признаками, то он может быть представлен как точка в k-мерном пространстве, и сходство с другими объектами будет определяться как соответствующее расстояние.

Характеристики близости объектов

Объединение или метод древовидной кластеризации используется при формировании кластеров несходства или расстояния между объектами. Эти расстояния могут определяться в одномерном или многомерном пространстве. Например, если вы должны кластеризовать типы еды в кафе, то можете принять во внимание количество содержащихся в ней калорий, цену, субъективную оценку вкуса и т.д. Наиболее прямой путь вычисления расстояний между объектами в многомерном пространстве состоит в вычислении евклидовых расстояний. Если вы имеете двух- или трёхмерное пространство, то эта мера является реальным геометрическим расстоянием между объектами в пространстве (как будто расстояния между объектами измерены рулеткой). Однако алгоритм объединения не «заботится» о том, являются ли «предоставленные» для этого расстояния настоящими или некоторыми другими производными мерами расстояния, что более значимо для исследователя; и задачей исследователей является подобрать правильный метод для специфических применений.

Евклидово расстояние является самой популярной метрикой в кластерном анализе. Оно попросту является геометрическим расстоянием в многомерном пространстве. Геометрически оно лучше всего объединяет объекты в шарообразных скоплениях.

Квадрат евклидова расстояния. Для придания больших весов более отдаленным друг от друга объектам можем воспользоваться квадратом евклидова расстояния путем возведения в квадрат стандартного евклидова расстояния.

Обобщенное степенное расстояние представляет только математический интерес как универсальная метрика.

Расстояние Чебышева. Это расстояние стоит использовать, когда необходимо определить два объекта как «различные», если они отличаются по какому-то одному измерению.

Манхэттенское расстояние (расстояние городских кварталов), также называемое «хэмминговым» или «сити-блок» расстоянием.

Это расстояние рассчитывается как среднее разностей по координатам. В большинстве случаев эта мера расстояния приводит к результатам, подобным расчетам расстояния евклида. Однако, для этой меры влияние отдельных выбросов меньше, чем при использовании евклидова расстояния, поскольку здесь координаты не возводятся в квадрат.

Процент несогласия. Это расстояние вычисляется, если данные являются категориальными.

Источник