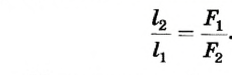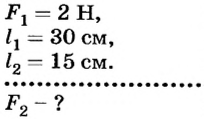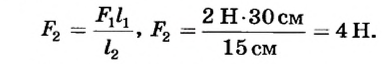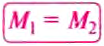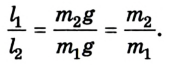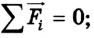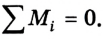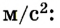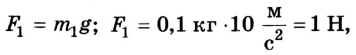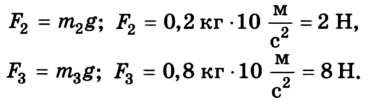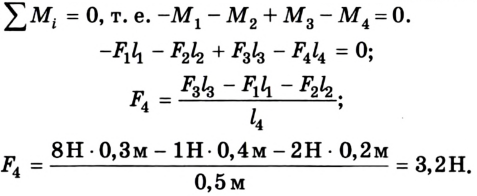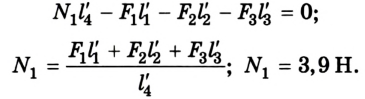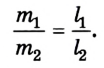Для чего используется рычаг

Что это рычаг в физике? Принцип работы рычага. Виды рычагов

Физическое понятие о рычаге

Вам будет интересно: Что такое ржавчина и как с ней бороться: оксиды железа

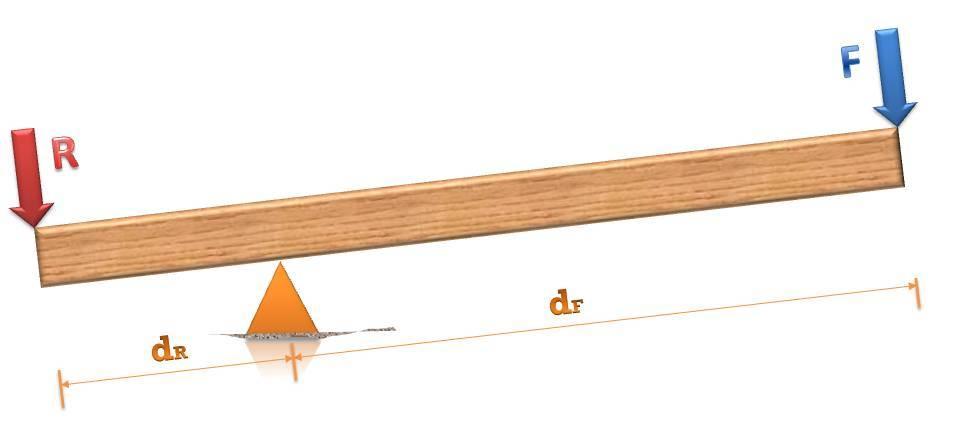
На рисунке выше показан рассмотренный простой механизм, который является рычагом первого рода (см. ниже).

Историческая справка

Каждый школьник слышал уже в 7 классе о знаменитом рычаге Архимеда. Греческий философ утверждал, что при определенных размерах этого простого механизма он мог бы перевернуть нашу Землю, будь вторая такая планета, которую можно было бы использовать в качестве опоры. Архимеду действительно принадлежит большая заслуга в развитии статики, поскольку он смог экспериментально получить математическое равенство, которое в настоящее время носит название «Условия равновесия рычага».

Однако сам принцип рычага использовался задолго до нашей эры. Так, известно, что для забора воды из рек применялся этот простой механизм. Существуют исторические свидетельства, что при строительстве пирамид египтяне также применяли систему рычагов.

Принцип работы рычага

Познакомившись с вопросом, что такое рычаг в физике (это наипростейший механизм), перейдем к рассмотрению принципа, согласно которому с помощью рычага получается выигрыш в силе или в пути перемещения. Для этого вспомним, что в физике существует величина, которая называется моментом силы. Последний равен произведению плеча силы на модуль силы, то есть:

Если вспомнить статику, то второе условие равновесия системы твердых тел в ней гласит, что система не будет совершать вращательного движения, если сумма всех n моментов сил в ней равна нулевому значению. То есть:

Прежде чем переходить к формулировке условия равновесия рычага, отметим, что момент силы, который стремится повернуть систему против часовой стрелки, является положительным. Противоположный ему момент будет отрицательным.

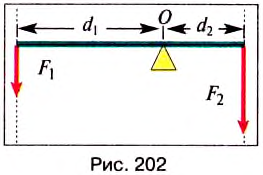
Выше показан рычаг, на который оказывают действие внешняя сила F и сила нагрузки R. Учитывая значение плеч сил и направления моментов, можно записать следующее равенство:

Откуда получаем условие равновесия рычага, полученное еще Архимедом:

Это условие говорит о том, что чем длиннее плечо dF, тем меньшую силу F следует приложить, чтобы поднять вес R. При этом высота подъема этого веса будет меньше, чем высота, на которую опустится плечо dF. Таким образом, при dF>dR получается выигрыш в силе, но проигрыш в пути. При обратном соотношении плеч получится выигрыш уже в пути, но силу F придется приложить большей величины, чем вес R.

Таким образом рычаг можно применять как для подъема тяжестей, так и для сообщения скорости телу весом R. Последнее раньше использовалось в катапультах.

Виды рычагов и примеры

В зависимости от положения опоры и порядка расположения действующих на балку сил рычаги бывают трех родов. Расскажем кратко об особенностях каждого из них.

В качестве рычагов третьего рода можно привести в пример рыбацкую удочку, пинцет или столовую вилку.

Источник

Рычаг

Рыча́г — простейшее механическое устройство, представляющее собой твёрдое тело (перекладину), вращающееся вокруг точки опоры. Стороны перекладины по бокам от точки опоры называются плечами рычага.

Рычаг используется для получения большего усилия на коротком плече с помощью меньшего усилия на длинном плече (или для получения большего перемещения на длинном плече с помощью меньшего перемещения на коротком плече). Сделав плечо рычага достаточно длинным, теоретически, можно развить любое усилие.

Частными случаями рычага являются также два других простейших механизма: ворот и блок.

Содержание

История

Человек стал использовать рычаг ещё в доисторические времена, интуитивно понимая его принцип. Такие инструменты, как мотыга или весло, применялись, чтобы уменьшить силу, которую необходимо было прикладывать человеку. В пятом тысячелетии до нашей эры в Месопотамии применялись весы, использовавшие принцип рычага для достижения равновесия. [1] [2] Позже, в Греции, был изобретён безмен, позволивший изменять плечо приложения силы, что сделало использование весов более удобным. Около 1500 года до н. э. в Египте и Индии появляется шадуф, прародитель современных кранов, устройство для поднимания сосудов с водой. [3]

Неизвестно, пытались ли мыслители тех времён объяснить принцип работы рычага. Первое письменное объяснение дал в III веке до н. э. Архимед, связав понятия силы, груза и плеча. Закон равновесия, сформулированный им, используется до сих пор и звучит как: «Усилие, умноженное на плечо приложения силы, равно нагрузке, умноженной на плечо приложения нагрузки, где плечо приложения силы — это расстояние от точки приложения силы до опоры, а плечо приложения нагрузки — это расстояние от точки приложения нагрузки до опоры». По легенде, осознав значение своего открытия, Архимед воскликнул: «Дайте мне точку опоры, и я переверну Землю!». [3]

В 1773 году Джеймс Уатт предложил идею составного рычага, состоящего из двух или нескольких связанных друг с другом рычагов, который можно было использовать для ещё большего увеличения усилия. Пример составного рычага, используемого в повседневной жизни, можно найти в щипчиках для ногтей. [3]

В современном мире принцип действия рычага используется повсеместно. Практически любой механизм, преобразующий механическое движение, в том или ином виде использует рычаги. Подъёмные краны, двигатели, плоскогубцы, ножницы, а также тысячи других механизмов и инструментов используют рычаги в своей конструкции.

Принцип действия

Принцип работы рычага является прямым следствием закона сохранения энергии. Чтобы переместить рычаг на расстояние сила, действующая со стороны груза, должна совершить работу равную:

.

Если посмотреть с другой стороны, сила, приложенная с другой стороны, должна совершать работу

,

где — это перемещение конца рычага, к которому приложена сила . Чтобы выполнялся закон сохранения энергии для замкнутой системы, работа действующей и противодействующей сил должны быть равны, то есть:

, .

По определению подобия треугольников, отношение перемещений двух концов рычага будет равно отношению его плеч:

, следовательно .

Учитывая, что произведение силы и расстояния является моментом силы, можно сформулировать принцип равновесия для рычага. Рычаг находится в равновесии, если сумма моментов сил (с учётом знака), приложенных к нему, равна нулю.

Для рычагов, как и для других механизмов, вводят характеристику, показывающую механический эффект, который можно получить за счёт рычага. Такой характеристикой является передаточное отношение, оно показывает, как соотносятся нагрузка и приложенная сила:

.

Составной рычаг

Составной рычаг представляет собой систему из двух и более простых рычагов, соединённых таким образом, что выходное усилие одного рычага является входным для следующего. Например, для системы из двух последовательно связанных рычагов, если на входное плечо первого рычага приложена сила , на другом конце этого рычага выходное усилие окажется , и связаны они будут с помощью передаточного отношения:

.

При этом на входное плечо второго рычага будет воздействовать такое же усилие , а выходным усилием второго рычага и всей системы будет , передаточное отношение второй ступени будет равно:

.

При этом механический эффект всей системы, то есть всего составного рычага, будет вычисляться как отношение входного и выходного усилия для всей системы, то есть:

.

Таким образом, передаточное отношение составного рычага, состоящего из двух простых будет равно произведению передаточных отношений входящих в него простых рычагов.

Такой же подход решения можно применять и для более сложной системы, состоящей, в общем случае из n рычагов. В этом случае в системе будет присутствовать 2n плеч. Передаточное отношение для такой системы будет вычисляться по формуле:

,

Как видно из формулы для этого случая также верно, что передаточное отношение составного рычага равно произведению передаточных отношений входящих в него элементов.

Типы рычагов [4]

Источник

Рычаги

Что из себя представляет рычаг в физике

Человек стал использовать рычаги еще в доисторическое время. Однако первое летописное упоминание об устройстве дал Архимед в III веке до н. э. Его закон равновесия гласил:

«Усилие, умноженное на плечо приложения силы, равно нагрузке, умноженной на плечо приложения нагрузки, где плечо приложения силы — это расстояние от точки приложения силы до опоры, а плечо приложения нагрузки — это расстояние от точки приложения нагрузки до опоры».

Рычаг — это простой механизм, который способен меньшей силой уравновесить большую. Он имеет вид твердого тела, вращающееся вокруг неподвижной опоры.

Рычаг используется для получения большего усилия на коротком плече с помощью меньшего усилия на длинном плече.

Рычаг первого и второго рода

Существуют несколько типов рычагов.

Рычаги первого рода — это такие приспособления, в которых точка опоры всегда располагается между точкой усилия и нагрузкой. Чтобы понять, как это работает, можно представить гвоздодер или весы.

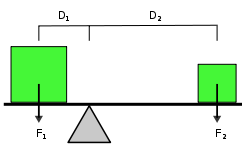
Рычаги второго рода — это такие механизмы, в которых на одном конце рычага находится точка опоры, а к другому прикладывается усилие. Груз, который необходимо поднять, располагается между точкой опоры и усилием.

За образец рычагов второго рода можно взять тачку для перевозки грузов. Груз находится между рукоятками тачки и колесом.

В наше время рычаги повсеместно используются во многих сферах жизни. Можно сказать, что почти любой механизм, производящий механическое движение в том или ином виде использует принцип действия рычага.

Рычаги в технике

Рычаги широко применимы в технике. Наиболее очевидный пример — рычаг переключения коробки передач в машине. Часть, что видна в салоне автомобиля, это короткое плечо рычага. Длинное плечо скрыто под днищем авто, оно длиннее короткого в два раза. Управляя коротким плечом рычага в машине, длинным плечом мы переключаем соответствующие механизмы.

Длина плеча рычага, диапазон его хода и сила, направленная на его сдвиг, взаимодействуют друг с другом.

Например, в спортивных автокарах, для более оперативного переключения передач, обычно устанавливают короткий рычаг, и уменьшают диапазон его хода. Однако в этот момент водителю необходимо приложить больше силы, чтобы переключить передачу.

В большегрузных автомобилях, где все механизмы сами по себе тяжелее, рычаг делают длиннее, и диапазон его хода так же длиннее, чтобы было проще управлять агрегатом.

Рычаги различного вида имеются у многих девайсов: педали или ручной тормоз велосипеда, ручка швейной машины, клавиши пианино — все это примеры рычагов.

Существует масса примеров рычагов на стройке: лом, экскаватор, подъемный кран. Строители используют такие приборы, как: кусачки, ножницы для резки бумаги или металла.

Примером рычага, дающего минус в силе, но плюс в расстоянии, является весло. Чем длиннее часть весла погружаемого в воду, тем больше его радиус вращения и скорость движения.

Рычаги в быту

Рычаги очень часто можно встретить в быту. Было бы необычайно сложно открыть туго завинченный водопроводный кран, если бы у него не было небольшой, но необходимой ручки, представляющей собой рычаг.

В качестве примера можно также рассмотреть гаечный ключ, предназначенный для откручивания или закручивания болта или гайки. Чем длиннее ключ, тем проще будет открутить гайку, или наоборот.

Дверь — это отличный пример рычага в будничной жизни. Практически невозможно открыть дверь, толкая ее возле крепления петель. Дверь будет открываться с трудом. Но чем дальше от дверных петель будет располагаться точка направления силы, тем легче будет распахнуть дверь.

С детства знакомое развлечение, качели для двоих, действуют тоже по принципу рычага. Есть неподвижная ось вращения, вокруг которой качели вращаются под действием сил тяжести детей. Чтобы перевесить своего друга, сидящего на противоположном сидении, поднять его, ребенок садится на самый край качели. Если он сядет ближе к опоре качели, может не перевесить.

Примеры рычагов в живой природе

Тело человека как рычаг

Опорно-двигательная система любого живого существа состоит из множества рычагов. Например, локтевой сустав. Лучевая и плечевая кости соединяются вместе хрящом. К ним, в свою очередь, присоединяются мышцы бицепса и трицепса. Место примыкания лучевой и плечевой костей — это своеобразная точка опоры. Таким образом образуется простейший механизм рычага.

Примеры рычагов в устройстве других живых существ

Наглядный пример применения преимуществ рычага в скелетно-мышечной системе живого организма — обратные задние колени у многих представителей животного мира (кошки, лошади и т.д.).

Их кости длиннее наших, они намного эффективнее использовать силу своих мышц, так как их задние ноги имеют специальное устройство. Хоть их мышцы сильнее чем у нас, их вес на порядок больше.

Лошадь в среднем весит около 450 кг, и при этом может без труда прыгнуть на высоту около двух метров. Чтобы повторить такой трюк, человеку надо быть мастером спорта по прыжкам в высоту, хотя люди имеют вес в среднем в 8-9 раз меньше, чем лошадь.

Меньшие по размерам существа также имеют в своем внутреннем устройстве рычаги: например, суставы насекомых. К тому же, клешни рака или краба действуют тоже как рычаг. Механизм клешней схож с принципом действия щипцов.

Источник

Содержание:

Рычаг:

Взаимодействие может происходить через промежуточные тела.

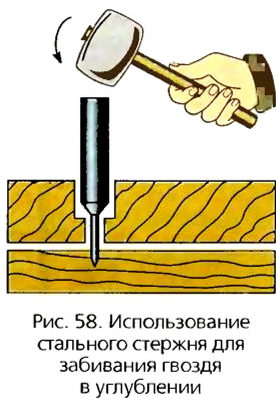
Взаимодействие может происходить не только при непосредственном контакте, но и при наличии промежуточных тел. Таких примеров можно привести большое количество. Так, если мастер забивает гвоздь в углублении, он ставит на головку гвоздя металлический стержень и по нему ударяет молотком (рис. 58). Молоток действует на стержень, который, в свою очередь, уже действует на гвоздь.

Можно ли изменять значения силы

Если взаимодействие между телами происходит через промежуточные тела, то можно изменять силы взаимодействия между ними. Оно может изменить как направление силы, так и ее значение. Одним из примеров такого использования промежуточных тел для взаимодействия между телами является рычаг. В быту и на производстве можно наблюдать много таких примеров.

Часто можно видеть, как тяжелый предмет поднимают или перемещают с помощью металлического стержня (рис. 59). В этом случае стержень называют рычагом.

Что такое рычаг

Рычагом называют жесткий стержень, имеющий ось вращения.

Под действием нескольких сил рычаг может вращаться или быть неподвижным. В последнем случае говорят, что рычаг уравновешен.

Как уравновесить рычаг

Выясним, при каких условиях рычаг, на который действует несколько сил, будет уравновешен.

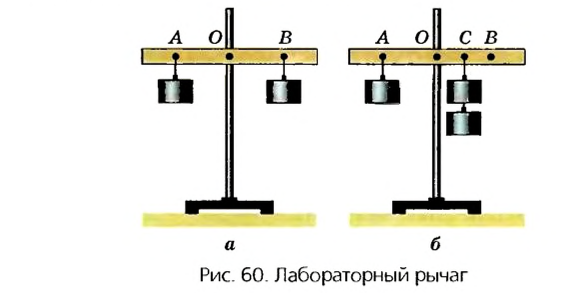
Для этого возьмем деревянную планку с отверстием посередине и поместим ее на оси, закрепленной в штативе (рис. 60). Это и будет рычаг. Слева от оси вращения повесим в точке А на расстоянии 10 см гирьку массой 102 г. В этом случае говорят, что точка А является точкой действия силы 1 Н. Под действием этой силы рычаг начнет вращаться против часовой стрелки. Для того чтобы он не вращался и оставался в горизонтальном положении, на другом конце рычага найдем такую точку В, при закреплении в которой гирьки массой 102 г рычаг перестанет вращаться. Измерив расстояние ОВ, увидим, что оно также равно 10 см. Таким образом, OA = ОВ, если F_l = F₂. Если направление действия силы перпендикулярно к направлению оси вращения рычага, то расстояние от его оси вращения к направлению действия силы называют плечом силы.

Если силы, действующие на рычаг, находящийся в равновесии, равны, то равны и плечи этих сил.

Если левую гирьку оставить прикрепленной в точке А, а в точке В подвесить две такие гирьки массой по 102 г каждая, то равновесие рычага нарушится и он начнет вращаться. Достигнуть равновесия в этом случае можно, изменяя положение точки подвеса двух гирек. Так можно установить новое положение точки подвеса С. Измерив оба плеча, увидим, что правое плечо ОС в два раза меньше левого плеча OA.

В случае равновесия рычага плечо большей силы меньше, и наоборот, плечо меньшей силы больше.

Используя свойства пропорции, получаем

В уравновешенном рычаге плечи сил обратно пропорциональны силам.

Что такое момент силы

Физическую величину, равную произведению силы на плечо, называют моментом силы. Единицей измерения момента силы является ньютон-метр (Н-м).

Сформулируем условие равновесия рычага в общем виде.

Рычаг пребывает в равновесии, если момент силы, вращающий рычаг по часовой стрелке, равен моменту силы, вращающему рычаг против часовой стрелки.

Конструктивно рычаг может быть таким, что силы будут действовать по одну сторону от оси вращения. Условие равновесия для него будет такое же, как и для рычага, рассмотренного выше.

Используя условие равновесия рычага, можно рассчитывать силы, действующие на него, или плечи этих сил.

Пример:

На одно из плеч рычага длиной 30 см действует сила 2 Н. Какая сила должна подействовать на другое плечо этого рычага длиной 15 см, чтобы он оставался неподвижным.

Дано:

Решение

При условии равновесия рычага 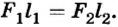Отсюда

Ответ. На второе плечо рычага должна подействовать сила 4 Н.

Где используют рычаги

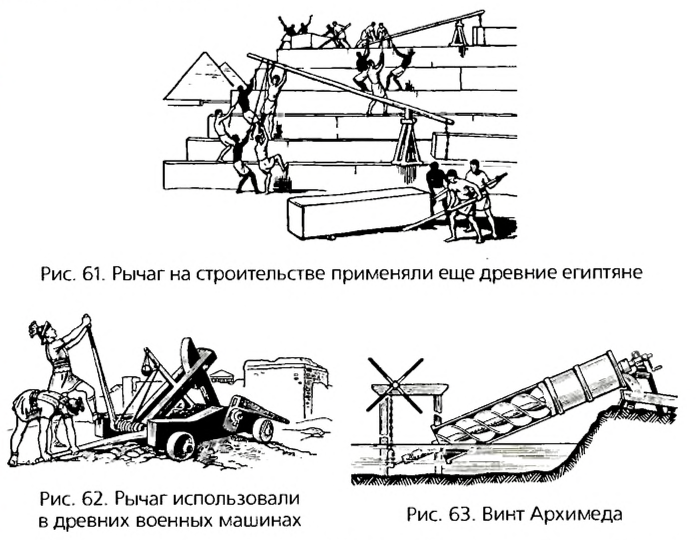
Рычаг известен человеку с того времени, когда человек взял палку, чтобы сбить плод с дерева. И вся следующая история человечества связана с использованием рычагов. Так, исследования историков показывают, что при строительстве пирамид древние египтяне использовали рычаги для поднятия тяжелых блоков на значительную высоту (рис. 61). Историкам науки известно, что древние римляне использовали рычаги для создания различных строительных и военных машин (рис. 62). Значительный вклад в теорию рычагов внес древнегреческий ученый и изобретатель Архимед. Сконструированные им машины помогали оборонять греческие города от захватчиков, подавать воду для орошения полей (рис. 63), перемещать значительные грузы на стройках, выполнять большое количество других подобных работ.

Рычаги широко используются и в современной технике, в самых разнообразных машинах.

Рычагом является стрела подъемного крана, используемого в строительстве. Она дает возможность получить выигрыш в силе или расстоянии. Момент силы, действующей на конце стрелы при подъеме груза, уравновешивается моментом противовеса, находящегося на противоположном конце стрелы.

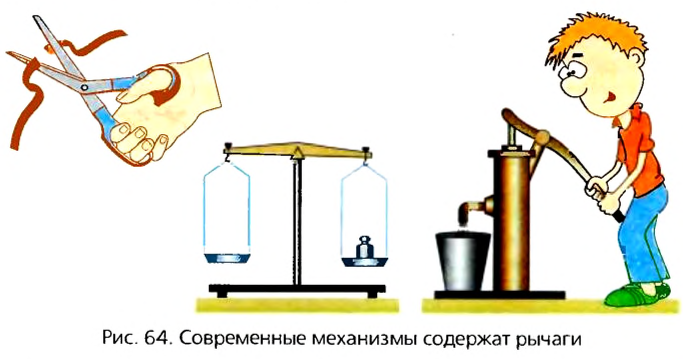
Принцип рычага используется во многих устройствах и инструментах, которыми мы пользуемся ежедневно. На рисунке 64 изображены некоторые из них. На них легко найти части, исполняющие роль рычагов.

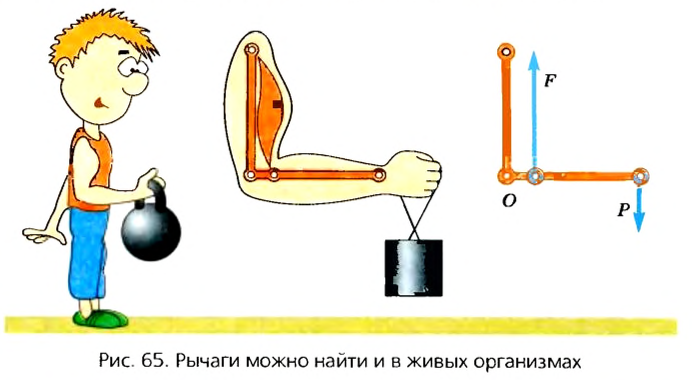
Рычаги можно найти и в живых организмах. По принципу рычага работают руки человека (рис. 65), ноги, голова.

Условие равновесия рычага и момент силы

Как уже отмечалось, рычаг — твёрдое тело, которое может вращаться около неподвижной опоры. Его применяют для изменения направления и значения силы, например для уравновешивания большой силы малой. Рычаг имеет следующие характеристики

Точка приложения силы — это точка, в которой на рычаг действует другое тело.

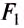
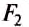
Ось вращения — прямая, проходящая через неподвижную точку опоры рычага О, и вокруг которой он может свободно вращаться. Рассмотрим случай, когда ось вращения расположена между точками приложения сил и .

Линия действия силы — это прямая, вдоль которой направлена сила.

Плечо силы — кратчайшее расстояние от оси вращения тела О до линии действия силы. Плечо силы обозначается буквой d. Единицей плеча силы в СИ является один метр (1 м).

Опыт. Возьмём рычаг, подобный изображённому на рис. 203. На расстоянии 10 см от оси вращения подвесим к нему 6 грузиков, каждый массой по 100 г. Чтобы уравновесить рычаг двумя такими же грузиками, нам придётся их подвесить с другой стороны рычага, но на расстоянии 30 см.

Следовательно, для того чтобы рычаг находился в равновесии, нужно к длинному плечу приложить силу, во столько раз меньшую, во сколько раз его длина больше длины короткого плеча. Такое правило рычага описывают формулой обратно пропорциональной зависимости: ,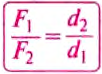

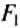
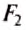
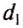
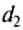
где и — силы, действующие на рычаг; и — плечи соответствующих сил. Поэтому правило (условие) равновесия рычага можно сформулировать так.

Рычаг находится в равновесии тогда, когда значения сил, действующих на него, обратно пропорциональны плечам этих сил.

С тех пор, когда Архимед установил правило рычага, оно просуществовало в первозданном виде почти 1900 лет. И лишь в 1687 г. французский учёный П. Вариньон придал ему более общую форму, используя понятие момента силы.

Момент силы М— это физическая величина, значение которой опре-Г деляется произведением модуля силы F, вращающей тело, и ее плеча d : .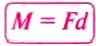

Единицей момента силы в СИ является один ньютон-метр (1 Н • м), равный моменту силы 1 Н, приложенной к плечу 1 м.

Докажем, что рычаг находится в равновесии под действием двух сил, если значение момента М₁ силы, вращающей рычаг против часовой стрелки, равно значению момента М₂ силы, вращающей его по часовой стрелке, т.е.:

Из правша рычага 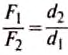на основе свойства пропорции вытекает

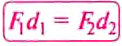
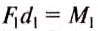
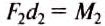
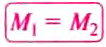
равенство:. Но — момент силы, вращающей рычаг против часовой стрелки (рис. 202),— момент силы, вращающей рычаг по часовой стрелке. Таким образом: ,

что и требовалось доказать. Итак, правило (условие) равновесия рычага можно ещё сформулировать так.

Рычаг находится в равновесии под действием двух сил, если значение момента силы, вращающей рычаг против часовой стрелки, равно значению момента силы, вращающей его по часовой стрелке.

Момент силы — важная физическая величина, она характеризует действие силы, показывает, что оно зависит и от модуля силы, и от её плеча. Например, мы знаем, что действие силы на дверь зависит и от модуля силы, и оттого, где приложена сила: дверь тем легче повернуть, чем дальше от оси вращения приложена сила, действующая на неё; гайку легче открутить длинным гаечным ключом, чем коротким; ведро тем легче вытянуть из колодца, чем длиннее ручка ворота.

Основы статики и равновесие рычага

Еще в давние времена люди использовали обычную палку в качестве рычага, выигрывая этим в силе. На рисунке 2.35 показано, как с помощью рычага можно поднять по ступенькам большие каменные глыбы, например для строительства пирамид.

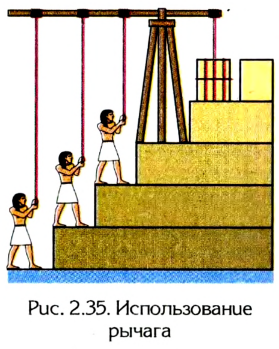
В древних книгах по механике, написанных учеными Греции и Египта, главным образом рассматривались вопросы статики. Важнейшие открытия в этой области принадлежали великому греческому философу Аристотелю, который и дал название «механика» науке, изучающей простейшие движения материальных тел, находящихся в природе или создающихся людьми в процессе их деятельности.

Ученые уже тогда понимали значение статики как одной из основных составляющих фундамента механики. Дальнейшее развитие науки и, особенно, техники подтвердило правильность их вывода: действие огромного количества £ механизмов и машин базируется на законах о равновесии сил.

Основы науки о равновесии были заложены еще Архимедом. Именно он ввел в физику такое понятие, как центр тяжести и момент силы относительно точки и оси, определил положение центра тяжести для многих тел и фигур, математически обосновал законы рычага, сформулировал правила приложения параллельных сил.

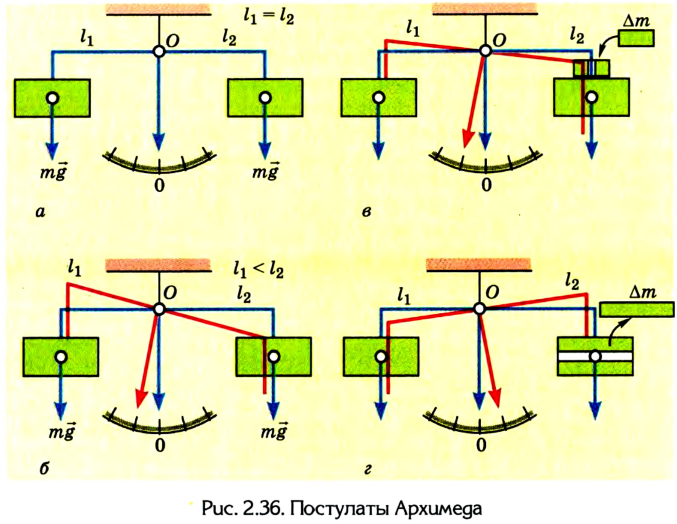
В своей работе «О равновесии плоских фигур» Архимед опирался на положения, которые считал само собой разумеющимися:

Рычаг находится в равновесии, если плечи сил обратно пропорциональны значениям сил, действующих на него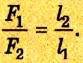

Из этих положений Архимед сделал вывод: грузы пребывают в равновесии, когда плечи рычага обратно пропорциональны грузам:

Условия равновесия тел. Устойчивое и неустойчивое равновесие

Вспомним, что момент силы относительно какой-либо оси равен произведению модуля силы на ее плечо: М = Fl. Плечом силы l называется кратчайшее расстояние от оси вращения до линии действия данной силы. Момент силы считается положительным, если сила стремится повернуть тело по часовой стрелке, и отрицательным, если такое действие противоположно. Для равновесия тел необходимы два условия: 1) геометрическая сумма приложенных к телу сил равна нулю:

2) алгебраическая сумма моментов сил относительно любой неподвижной оси равна нулю:

Момент силы: М = Fl.

Условия равновесия тел:

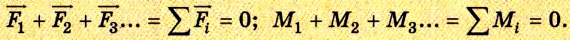
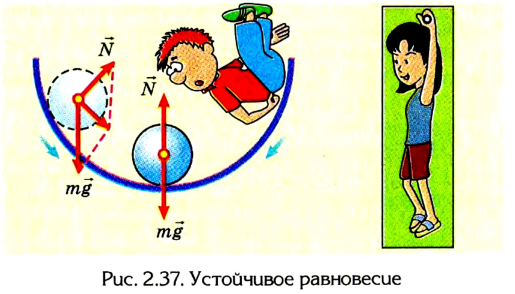
Равновесие устойчивое, если при незначительном смещении тело вновь возвращается в положение равновесия (рис. 2.37).

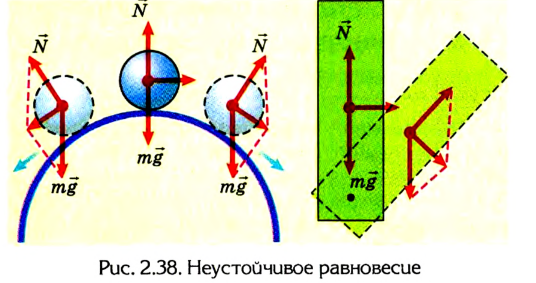
При неустойчивом равновесии незначительное смещение тела вызывает в дальнейшем значительное удаление его от исходного положения (рис. 2.38).

Равновесие тела может быть устойчивым, неустойчивым и безразличным.

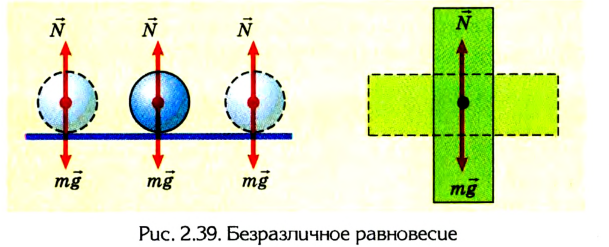
Если любые смещения тела не нарушают его состояния равновесия, то можно говорить о безразличном равновесии (рис. 2.39).

Примеры решения задач на равновесие рычага

Рассмотрим примеры решения задач статики.

Пример №1

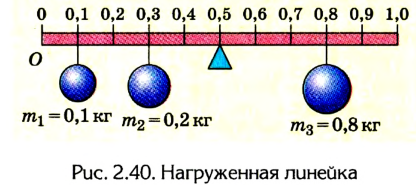
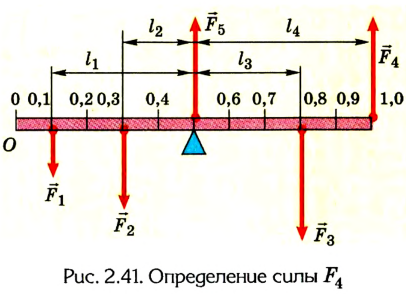
Метровая линейка, весом которой можно пренебречь, положена средним делением на подставку и нагружена гирями (рис. 2.40). Какого направления и значения сила должна быть приложена на делении 1 м для того, чтобы линейка находилась в равновесии? Какой будет сила реакции опоры, если приложить эту силу?

Решение:

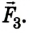
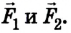
Выполняем рисунок в соответствии с условием задачи (рис. 2.41), указав силы и их плечи. Линейка под действием моментов сил может вращаться вокруг неподвижной оси О, которая проходит через точку О. Будем считать положительными все моменты, вращающие систему по часовой стрелке. В задаче это момент силы Отрицательные моменты создают силы

Для упрощения вычислений значение ускорения свободного падения будем считать равным 10

Предположим, что для равновесия системы на конце линейки 1 м должна быть приложена сила 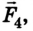направленная вертикально вверх. Если же мы ошиблись в выборе направления этой силы, то в ответ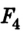е значение силы получится со знаком «-«. Для решения задачи воспользуемся вторым условием равновесия тела:

Ответ:= 3,2H, направление силы выбрано правильно.

Пример №2

Метровая линейка, весом которой можно пренебречь, положена крайними точками на две опоры и нагружена гирями, как в предыдущей задаче. Нужно определить силы реакции опор 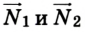(рис. 2.42).

Решение:

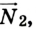
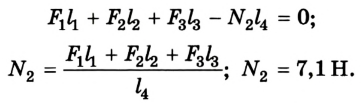
Чтобы определить силу реакции опоры можно воспользоваться таким приемом. Если опору забрать, то для равновесия системы на отметке 1 м необходимо приложить силу, направленную вертикально вверх. Иначе система будет вращаться вокруг оси в точке О линейки по часовой стрелке. Теперь можно применить правило моментов:

Чтобы определить силу реакции опоры 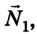действуем аналогично. Теперь система будет вращаться вокруг оси против часовой стрелки, когда она проходит через отметку 1 м:

Чтобы найти силы реакции опор, можно воспользоваться правилом сложения параллельных сил. Им же можно пользоваться и для контроля найденных значений.

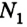
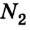
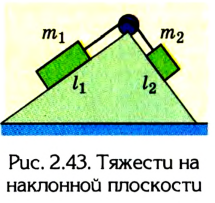
Ответ: = 3,9 H; =7,1 Н.

Оригинальный метод решения задач статики был предложен Симоном Сте-вином (1548-1620). Для случаев равновесия тел на наклонной плоскости он доказал, что массы тел соотносятся как длины плоскостей, которые их образуют (рис. 2.43):

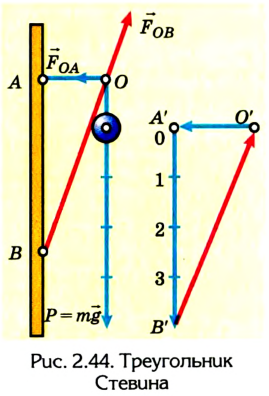
Он же установил принцип сложения статических сил (треугольник сил): три силы, действующие на одну точку, находятся в равновесии тогда, когда они бывают параллельны и пропорциональны трем сторонам плоского треугольника (рис. 2.44). Приведем пример решения одной из задач статики с применением треугольника сил.

Пример №3

На кронштейне висит лампа весом 4 Н. Найти значение сил упругости в деталях ОА и ОВ.
Дано:

Решение:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник