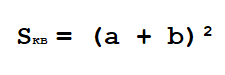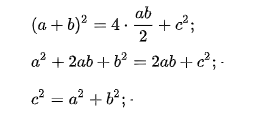Для чего используется теорема пифагора
Теорема Пифагора: история, формулы и доказательства
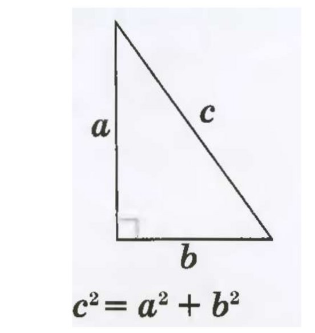
Теорема Пифагора – одна из самых известных геометрических теорем, которая устанавливает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Большинство ученых считают, что теорема Пифагора была доказана древнегреческим математиком и философом Пифагором (или Питагором). Однако есть версия, что теорему знали и до его рождения. Доказательством этого является то, что в Древнем Египте знали, что треугольник, у которого стороны имеют 3 см, 4 см и 5 см, является прямоугольным. А о других теоремах можно узнать в учебнике по геометрии за 8 класс А.Г. Мерзляка.
Еще в детстве Пифагор отличился интересом к точным наукам. Впоследствии он переехал жить на остров Лесбос, где познакомился с Фалесом Милетским – древнегреческим философом и математиком, который доказал теоремы о трех точках на окружности и пропорциональных отрезках. За время, когда Пифагор учился в Милетской школе, он изучал астрологию, медицину, прогнозы затмений и другие важные в то время науки. Лекции Фалеса и его ученика Анаксимандра сыграли важную роль для Пифагора.
После обучения в Египте, плена в Вавилоне, в 60 лет Пифагор решает вернуться домой, чтобы поделиться своими знаниями с народом. Впоследствии он открыл собственную школу, в которой геометрия впервые выступает как самостоятельная наука.
О том, что квадрат гипотенузы равен сумме квадратов катетов, знали задолго до рождения Пифагора. Но именно он считается первым ученым, который доказал соотношение сторон треугольника.
В теореме Пифагора говорится, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Пусть ВС = а; АС = b; АВ = с.
Тогда имеем такую формулу, которая применяется при нахождении неизвестной стороны в прямоугольном треугольнике, когда две другие – известны:
Когда мы определили квадрат гипотенузы, нужно найти квадратный корень. Такую же формулу мы можем применить к неизвестному катету:
А больше рисунков и формул можно увидеть в онлайн уроке за 8 класс по геометрии на тему «Метрические соотношения в прямоугольном треугольнике. Теорема Пифагора».
Самый популярный и самый простой метод доказательства теоремы связан с площадями фигуры.
Нужно расположить одинаковые прямоугольные треугольники так, чтобы внутри образовался квадрат. Каждая сторона внешнего квадрата должна состоять из суммы катетов прямоугольного треугольника a + b.
Площадь этого квадрата можно будет найти благодаря формуле:
Внутренний четырехугольник можно считать квадратом, ведь, если добавить два острые углы прямоугольного треугольника, то получится 90°. Следует считать, что площадь внешнего квадрата состоит из площади внутреннего квадрата и четырех площадей одинаковых прямоугольных треугольников. Итак, в заключении:
Итак, теорема Пифагора доказана.
2. Доказательство Евклида
Доказательство Евклида также называется «Пифагоровы штаны». Ее так назвали, потому что сумма площади квадратов, образованных с использованием катетов прямоугольного треугольника равна площади квадрата, который построен на гипотенузе этого же треугольника. Квадраты напоминали ученикам мужские штаны.
На примере приведенных картинок ниже можно увидеть, как оригинально передали суть доказательства Евклида.
В вашем учебнике не было таких доказательств? Вы можете найти другой в разделе «Учебники по геометрии за 8 класс».
Пример задачи на применение теоремы Пифагора
Условия задачи. В треугольнике ABC дано: ∠C = 90 °, BC = 20 см, AC = 15 см. Найти сторону AB.
Решение. Поскольку в треугольнике АВС ∠С = 90°, следовательно, по теореме Пифагора имеем:
АВ² = BС² + АС²; AВ² = 20² + 15², AВ² = 625, AB = √625| AB = 25 см.
Если вам нужно решить задачу с помощью теоремы Пифагора, а вы сомневаетесь в конечном ответе, тогда можете проверить свои знания благодаря разделу «ГДЗ и решебники по геометрии за 8 класс».
А если вы хотите крепче закрепить знания по другим темам по геометрии, то можете просматривать видео в разделе «Онлайн уроки за 8 класс по геометрии». Узнайте больше о перпендикуляре и наклонной, сумме углов выпуклого треугольника, площадь квадрата и прямоугольника, решение задач методом площадей и тому подобное.
ПРОЕКТ на тему «Теорема Пифагора и ее практическое применение по математике»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа № 50»
ПРОЕКТ
на тему «Теорема Пифагора и ее практическое применение»
по математике
Ученицы 8 класса
Данилян Ева
Руководитель проекта: учитель математики
Гаджиева Саида Гамзаевна
г. Махачкала
2021 г.
1.1 Биография Пифагора……………………………………………. 4
1.2 История теоремы и её формулировка…………………………………. 4
2.1 Исследование знаний о теореме………………………………. 6
2.2 Применение теоремы в различных областях жизни…………………. 7
Заключение………………………………………………………….…………. 13
Объект исследования. Теорема Пифагора.
Гипотеза. Если теорема Пифагора так популярна и сегодня, то в ней заложены такие основы, которые позволяют использовать её в широком диапазоне.
Цели и задачи. Цель работы – показать значение теоремы Пифагора не только в математике, но и других отраслях нашей повседневной жизни.
Исходя из цели, были поставлены следующие задачи:
1. Найти в различных источниках и проанализировать найденную информацию о теореме и биографии Пифагора.
2. Изучить историю появления и развития теоремы Пифагора.
3. Провести опрос среди учащихся в виде анкетирования для выявления знаний о теореме Пифагора.
4. Установить какое значение имеет открытие теоремы в развитии математики.
5. Выяснить где может применяться теорема в повседневной жизни.
6. Обработать полученные данные и сделать вывод.
Г лава I . Основное содержание
1.1 Биография Пифагора.
В Кротоне Пифагор выступил организатором собственной школы, которая была одновременно и политической структурой, и религиозно-монашеским орденом со своим уставом и очень строгими правилами.
Прокатившаяся в то время волна демократических восстаний в Греции и колониях докатилась и до Кротона. После победы демократии Пифагор с учениками переселяется в Тарент, позднее в Метапонт. Когда они прибыли в Метапонт, там бушевало народное восстание, и в одном из ночных побоищ Пифагор погиб. Тогда он был глубоким старцем, ему было около 80 лет. Вместе с ним прекратила существование и его школа, ученики рассредоточились по всей территории страны.
Поскольку Пифагор считал свое учение тайной и практиковал только устную передачу его ученикам, собрания сочинений после него не осталось. Некоторые сведения все-таки стали явными, однако разграничить истину и выдумки невероятно сложно.
1.2 История теоремы и её формулировка.
Сегодня уже не проверишь, кто прав, а кто заблуждается. Известно лишь, что доказательства Пифагора, если оно когда-либо существовало, не сохранилось. Впрочем, высказываются предположения, что знаменитое доказательство из «Начал» Евклида может принадлежать как раз Пифагору, и Евклид его только зафиксировал.
Также мне оказался интересен тот факт, что задачи о прямоугольном треугольнике встречаются в египетских источниках времен фараона Аменемхета I, на вавилонских глиняных табличках периода правления царя Хаммурапи, в древнеиндийском трактате «Сульва сутра» и древнекитайском сочинении «Чжоу-би суань цзинь».
Во времена Пифагора теорема звучала так: «доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника равновелик сумме квадратов, построенных на катетах» или «площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.
В современных учебниках теорема гласит: «в прямоугольном треугольник квадрат гипотенузы равен сумме квадратов катетов».
Глава II . Практическая часть.
2.1 Исследование знаний о теореме.
В школьном курсе геометрии с помощью теоремы Пифагора решаются только математические задачи. К сожалению, вопрос о практическом применении теоремы рассматривается крайне редко. Теорема Пифагора самая известная теорема в геометрии, о ней знает подавляющее большинство населения планеты. В связи с этим, мне стало интересно проанализировать знания по этому вопросу среди своих сверстников. Я провела в школе опрос на тему: «Знаете ли Вы теорему Пифагора?» Были получены следующие результаты:
Теорема Пифагора и её практическое применение
Управление образования администрации Беловского района
МОУ «Старопестеревская средняя общеобразовательная школа»
«Теорема Пифагора и её
I. Историческая справка о Пифагоре…………………………………5
II. Доказательства теоремы Пифагора…………………………………6
III. Использование теоремы Пифагора в решении задач…………..13
IV. Практическое применение теоремы Пифагора
1) архитектура и строительство………………………………..…21
(ок. 580 – ок. 500 г. до н. э.)
Пребудет вечной истина, как скоро
Её познает славный человек!
И ныне теорема Пифагора верна,
Как и в его далёкий век.
Инструментами нашего исследования являются следующие аспекты:
а) объект исследования – т. Пифагора;
б) субъект исследования – геометрическое пространство;
в) предмет исследования – применение т. Пифагора.
В данном исследовании мы попытались объединить и систематизировать самые разные стороны применения теоремы Пифагора. Кроме того, мы рассмотрели личность Пифагора, обратили внимание на различные доказательства этой теоремы и решения множества задач по её практическому применению в различных сферах жизни.
Цель: доказать, что «простота, красота и универсальность» теоремы Пифагора позволяет использовать её в различных сферах науки и жизни.
· рассмотреть гипотезы об авторстве доказательства теоремы Пифагора;
· продемонстрировать способы доказательства теоремы Пифагора (например, одно из доказательств «Пифагоровы штаны во все стороны равны»);
· показать применение теоремы Пифагора при решении задач;
· рассмотреть её практическое применение в архитектуре, строительстве, мобильной связи, астрономии.
В своей исследовательской работе использовали монографии по математике, исследовательские разработки, материалы периодической печати, Интернет-ресурсы, мультимедийные компьютерные технологии. В работе представлен объёмный иллюстративный материал в виде таблиц, чертежей, иллюстраций, фотоснимков, рисунков, математических расчётов. Во всех расчетах оперировали приближёнными числовыми значениями величины, так как первоначальные исходные данные получали путём измерений.
Мы представляем результат работы над проектом в виде электронной презентации. Практическое применение нашей работы – использование нашего проекта для элективных курсов, предпрофильной и профильной подготовках и на факультативных занятиях.

Пифагор Самосский родился около 580 г. до н. э. на острове Самос в Ионическом море. Пифагор – едва ли не самый популярный учёный за всю историю человечества.
Он принимал в свою школу только тех юношей, которые промолчали в течение пяти лет. Значит, при занятиях математикой нужна абсолютная тишина для того, чтобы можно было сосредоточить все внимание на решении того или другого утверждения.
Пифагор был не только учёным, но и основателем первой научной школы. Он был и воспитателем душ, проповедником собственной «пифагорейской» этики, философом, которого по силе духа и силе воздействия можно сравнить разве с его великими современниками: Конфуцием, Буддой. Но в отличие от них Пифагор создал самую яркую «религию». Он воспитывал в человеке веру в могущество разума, убеждённость в познаваемости природы, уверенность в том, что ключом к тайнам мироздания является математика.
2500 лет тому назад Пифагор направил людей по пути торжества разума. Легенды наперебой объявляют Пифагора чудотворцем. Сообщают, что у него было золотое ребро, что люди видели его одновременно в двух разных городах говорящим со своими учениками, что, однажды, когда он с многочисленными спутниками переходил реку и заговорил с ней, река вышла из берегов и громким голосом воскликнула: «ДА здравствует Пифагор!» Сообщали, что в Тиррении он умертвил своим уксусом ядовитую змею, унёсшую многие жизни. Что он предсказывал землетрясения, отвращал ураганы, укрощал морские волны, останавливал повальные болезни. Порфирий рассказывал о Пифагоре такую историю, что в Торренте он увидел быка, жевавшего новые бобы, подошёл к пастуху и посоветовал сказать быку, чтобы тот этого не делал. Пастух засмеялся и сказал, что он не умеет говорить по-бычьи. Тогда Пифагор сам подошёл к быку и прошептал ему что-то на ухо; после чего бык не только пошёл прочь из бобовника, но и никогда не касался бобов. В 1808 году в Санкт-Петербурге вышла карманного формата книжка «Пифагоровы законы и нравственные правила». Вот некоторые извлечения из этой книги, содержащей 325 заповедей.
Доказательство теоремы Пифагора.
Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдём:
Катеты в квадрат возводим,
Сумму степеней находим –
И таким простым путём
К результату мы придём.
Сегодня известно около 500 различных доказательств теоремы Пифагора геометрических, алгебраических, механических и прочих.
Трудно найти человека, который не знал бы её шуточную формулировку: «Пифагоровы штаны во все стороны равны».
А 


 |
Площадь большого квадрата равна сумме площадей маленького квадрата и площадей 4-х треугольников

Рассмотрим один из примеров доказательства теоремы Пифагора.
 |
1) Достроим треугольник до квадрата со
Вычтем из обеих частей 2ав, тогда:
с2=а2+в2,что и требовалось доказать.
1) Прямоугольные треугольники равны по
2) Внутри получается квадрат, т. к. этот
четырёхугольник ромб с прямым углом.



Решение практических задач на применение теоремы Пифагора.

Better Explained: удивительные применения теоремы Пифагора
Мы привыкли думать, что теорема Пифагора — это что-то про геометрию и треугольники. На самом деле область её применения гораздо шире, и автор ресурса Better Explained готов это доступно объяснить.
Теорема Пифагора — настоящая знаменитость в мире математики: уж если её формула засветилась в сериале «Симпсоны», она точно известна всем.
Большинство считает, что формула теоремы Пифагора применима только в геометрии и только к треугольникам. Скорее всего, при упоминании этой теоремы вы вспоминаете что-то такое:
А теперь вдумайтесь: теорема Пифагора работает для любых фигур и для всех квадратных уравнений.
Если вы продолжите читать статью, вы узнаете, как эта теорема возрастом в 2,5 тысячи лет может помочь нам разобраться в информационных технологиях, физике и даже в полной мере оценить силу социальных сетей.
Идём к пониманию площади
Всегда увлекательно посмотреть на привычное под новым углом. К примеру, до написания этой статьи я никогда не задумывался о глубинном понятии такого явления, как «площадь фигуры». Да, мы можем помнить формулы, но вот понимаем ли мы саму природу площади?
Удивительно, но площадь любой фигуры может быть вычислена путём возведения в квадрат любого линейного сегмента. Линейный сегмент — это отрезок прямой, который мы выбираем в геометрической фигуре. Например, в качестве линейного сегмента квадрата мы выбрали сторону. Тогда площадью квадрата является квадрат его стороны (сторона = 5, площадь = 25). В качестве линейного сегмента круга можно взять радиус, и тогда площадью круга будет являться число π, умноженное на квадрат его радиуса (радиус = 5, площадь = 25π). Куда проще?
Мы можем взять любой линейный сегмент и с его помощью вычислить площадь: каждый линейный сегмент, возведённый в квадрат, даст нам величину площади фигуры, если его помножить на определённый коэффициент. Так мы получаем универсальную формулу расчёта площади фигуры:
Площадь фигуры = Коэффициент * (линейный сегмент)²
Посмотрите на диагональ d квадрата. Сторона квадрата при этом будет вычисляться как d, поделённая на √2. В этом случае площадь квадрата будет вычисляться как 1/2 d². Если мы хотим использовать диагональ фигуры в качестве линейного сегмента, нашим коэффициентом будет являться число 1/2.
А теперь в качестве линейного сегмента используем периметр p. Сторона квадрата — это p/4, значит, его площадь вычисляется по формуле p²/16. В этом случае коэффициентом для p² будет являться 1/16.
А можно взять вообще любой линейный сегмент?
А как же! Между «традиционным» сегментом (ну, например, стороной квадрата) и любым другим по вашему вкусу (скажем, периметром) всегда существует взаимосвязь (несложно догадаться, что периметр будет равен четырём сторонам квадрата). Если мы можем конвертировать новый сегмент в традиционный, площадь вычисляется легко — изменится лишь коэффициент в уравнении.
А можно взять вообще любую геометрическую фигуру?
Почти. Универсальная формула работает для всех подобных фигур — тех, что являются увеличенными или уменьшенными версиями одной и той же фигуры. Ну, например:
Все квадраты похожи друг на друга (площадь квадрата — всегда квадрат одной его стороны). Все круги похожи друг на друга (площадь круга — всегда π*r²). Треугольники не похожи друг на друга: они бывают вытянутыми или плоскими, «толстенькими» и «тоненькими», и у каждого треугольника — свой коэффициент для вычисления площади в зависимости от того, какой линейный сегмент вы выбрали. Измените форму треугольника, изменится и уравнение.
В целом все треугольники подчиняются правилу «площадь = 1/2 основания * высоту». Но отношения между основанием и высотой зависят от вида треугольника, поэтому и коэффициент в универсальной формуле будет всегда разным.
Почему для сохранения универсальности уравнения необходимы подобные фигуры? Интуитивно понятно, что при масштабировании фигуры вы меняете её размер, но сохраняете пропорции. Периметр квадрата всегда будет вычисляться умножением размера его стороны на 4.
Поскольку коэффициент в формуле площади основывается на отношениях между элементами фигуры, формула будет работать для всех фигур с одинаковыми пропорциями (подобными фигурами). Это как сказать, что полный размах рук человека приблизительно соответствует его росту — вне зависимости от того, кто перед нами, ребёнок или баскетболист.
Так вот, основная концепция расчёта площади фигуры может быть выражена в следующих трёх постулатах:
Интуитивное понимание теоремы Пифагора
Никто не спорит с тем, что теорема Пифагора работает. Но почти все её доказательства основаны на механических действиях: переставляем местами фигуры, и вуаля! — уравнение всё равно работает. Давайте подумаем: вам правда интуитивно понятно, что уравнение должно выглядеть как a² + b² = c²? А почему не 2a² + b² = c²? Давайте попробуем найти в этом смысл.
Для начала нам понадобится осознать и принять удивительный факт: любой прямоугольный треугольник можно разбить на два подобных прямоугольных треугольника.
Круто, да? Всего один опущенный перпендикуляр, и один треугольник превращается в две свои маленькие копии.
Собственно, этот пример говорит нам об очень простой вещи:
Площадь (чего-то большого) = Площадь (кое-чего среднего) + Площадь (кое-чего поменьше)
Маленькие треугольники были получены из большого, поэтому мы просто складываем их площади. И да, самое главное: поскольку треугольники подобны, для них действует одна и та же формула вычисления площади.
Давайте назовём длинную сторону (с длиной 5) — с, среднюю сторону (с длиной 4) — b, и короткую сторону (с длиной 3) — a. Формула площади для этих треугольников выглядит так:
Площадь = F*гипотенуза²,
где F — это множитель (в этом случае — 6/25 или 0,24). С формулой можно поиграть:
Площадь (чего-то большого) = Площадь (кое-чего среднего) + Площадь (кое-чего поменьше)
Fc² = Fb² + Fa²
Просто уберите F, и вы получите:
c² = b² + a²
Ой, так это же наша любимая теорема! Мы знали, что она нас не подведёт, но теперь мы понимаем, почему:
Конечно, теорема Пифагора работает только в Евклидовой геометрии и не может применяться, например, к сферам. Но об этом нужно поговорить в другой раз.
Применение теоремы: Возьмём любую фигуру
Ранее мы использовали простую плоскую фигуру — треугольник. Но ведь линейный сегмент можно извлекать из абсолютно любой фигуры. Возьмём, к примеру, круг. На изображении мы видим три разных круга с радиусами, равными сторонам нашего пифагоровского треугольника.
Можно ли с большим кругом поступить так же, как мы поступили с большим треугольником — сложить площади меньших кругов? При этом мы будем помнить, что площадь каждого маленького круга мы можем высчитать, используя квадрат известного нам линейного сегмента, умноженный на конкретный коэффициент — в данном случае это будет число Пи.
Да-да, всё верно: Площадь круга радиусом 5 = Площадь круга радиусом 4 + Площадь круга радиусом 3.
Мы запросто подставляем в формулу нужный коэффициент, и она всё ещё работает.
Помните, что в качестве линейного сегмента может выступать любой элемент плоской фигуры. Вы могли выбрать радиус, диаметр или длину окружности — изменился бы только коэффициент, но отношения 3-4-5 остались бы неизменными.
Теорема Пифагора позволяет находить соотношение площадей любых подобных фигур. Это то, чему нас не учат в школе.
Применение теоремы: сохранение квадратов
Теорема Пифагора применяется к любому квадратному уравнению. Подобно тому, как вы разбиваете треугольники, вы можете разбить квадрат любого количества чего угодно (c²) на более малые его доли (a²+b²). Этим «чем угодно» может быть расстояние, энергия, человекочасы, время или количество пользователей в социальной сети.
Социальные сети.
Есть такой закон — закон Меткалфа, формулирующий уровень полезности социальной сети: он говорит, что ценность социальной сети растёт в квадратичной зависимости от количества пользователей в ней. Например:
Сеть из 50 млн. пользователей = Сеть из 40 млн. пользователей + Сеть из 30 млн. пользователей
Кажется удивительным, что полезность социальной сети в 50 миллионов человек выражается через полезность двух соцсетей, в сумме имеющих 70 миллионов человек, но это на самом деле так. Социальная сеть растёт нелинейно.
Информационные технологии.
Некоторым программам требуется n² времени для обработки n запросов. Другими словами:
50 запросов = 40 запросов + 30 запросов
Удивительно, но 70 элементов данных, разбитые на две группы, будут обработаны так же быстро, как одна группа из 50 элементов. Именно поэтому имеет смысл сортировать элементы по группам и подгруппам. Эта особенность используется почти во всех алгоритмах сортировки. Теорема Пифагора помогает понять, почему сортировка 50 элементов сразу менее эффективна, чем сортировка этого же количества элементов по отдельности.
Площадь поверхности.
Площадь поверхности сферы определяется как 4πr². Что это значит?
Площадь радиусом 50 = Площадь радиусом 40 + Площадь радиусом 30
В жизни нам встречается не так уж и много сфер, но вот портовым работникам это знание весьма полезно (в конце концов, корпус любого судна — это деформированная сфера). Количеством краски, необходимой для 50-тифутовой яхты, можно окрасить две яхты длиной 40 и 30 футов.
Физика.
Если вспомнить школьные уроки физики, можно привести в пример формулу расчёта кинетической энергии объекта массой m при скорости v: 1/2mv². Применяем теорему Пифагора.
Энергия при скорости в 500 км/ч = Энергия при скорости в 400 км/ч + Энергия при скорости в 300 км/ч
Значит, одного и того же количества энергии хватает либо на запуск одного предмета на скорости 500 км/ч, либо на запуск двух других на меньшей скорости.
Попробуйте сами
В теорему Пифагора можно подставлять абсолютно любые цифры. Она может помочь нам и в повседневной жизни. Например, мы никак не можем выбрать: заказать большую пиццу диаметром 50 см или две диаметром 30 см? Мы с теоремой уже знакомы хорошо и нас не обмануть: площадь одной пиццы в 50 см будет действительно больше, чем площадь двух пицц по 30 см в диаметре (можете проверить, мы не обманываем). Всегда можно подставить другие цифры, а для ленивых есть простой и удобный калькулятор.
Наслаждайтесь
Со школьной скамьи мы уверены, что теорема Пифагора — это что-то о треугольниках и геометрии. Мы с вами вместе убедились, что это не так.
Помните, что стороны прямоугольного треугольника могут превратиться в линейный сегмент любой фигуры, и стать переменными в любом квадратном уравнении. И это ошеломительно.
Спасибо великолепной статье на BetterExplained.