Для чего используется цилиндрическая проекция
Цилиндрические проекции и области их применения.
Цилиндрическая проекция – вспомогательная поверхность цилиндр. Все параллели и меридианы имеют равную длину. На полюсах гиперискажение из-за равных параллелей.
Цилиндрические проекции могут быть как нормальными, так и поперечнами или косыми.
По свойствам изображения проекции могут быть равноугольными, равновеликими и произвольными.
Цилиндрические проекции находят разнообразное применение. Могут быть использованы для обзорного изображения земной поверхности. Равноугольная цилиндрическая используется для навигации. В России используют поперечную цилиндрическую проекцию Гаусса – Крюгера для составления миллионной карты.
Конические проекции и области их применения.
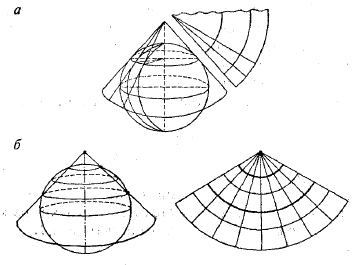
Коническая проекция – вспомогательная поверхность конус, касающийся шара по определенной параллели. Меридианы – прямые радиальные линии из полюса, параллели – дуги концентрической окружности. Также могут быть нормальными, поперечными, косыми.
По характеру искажений конические проекции могут быть различными. Наибольшее распространение получили равноугольные и равнопромежуточные проекции.
Эти проекции пригодны для территорий, расположенных в средних широтах, имеющих широтную вытянутость. Применяют для карт территорий, вытянутых вдоль параллелей
Азимутальные проекции и области их применения.
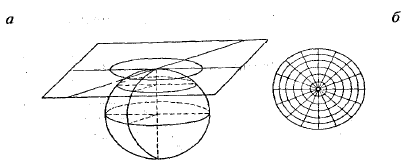
Для построения азимутальной проекции используется плоскость, касательная к шару в точке полюса. Параллели – концентрические окружности. Меридианы – линии из центра.
Бывает также азимутальная поперечная и азимутальная косая проекция. Распространена азимутальная поперечная – экваториальная проекция (осевой меридиан и экватор – прямые. Остальное – симметричные относительно них дуги)
Азимутальная проекция применяется в основном при картировании арктических и антарктических областей. Экваториальная азимутальная для карт полушарий и Африки. Косая азимутальная для Австралии, Америки.
Классификация проекций по характеру искажений. Области применения проекций с разным характером искажений.
Равновеликие – искажения площадей нет, но очень сильно нарушается форма фигур. Эллипс искажения имеет постоянную площадь, но сжимается к полюсам. Расстояние между параллелями от экватора к полюсам уменьшается. Значительны искажения углов и форм.
Равноугольные – углы на карте равны углам на эллипсоиде. Эллипс искажения всегда окружность, но он увеличивается к полюсам. Расстояние между параллелями увеличивается от экватора к полюсам.
Главным примером данной проекции является поперечно-цилиндрическая Проекция Меркатора (1569г)
Все проекции с разными показателями искажения – произвольные. Из произвольных выделяется равнопромежуточная проекция.
Равнопромежуточная проекция с равным балансом искажения площадей и углов. Эллипс искажения меняет и площадь и форму. Расстояние между параллелями равно.
Различают равнопромежуточные проекции по меридианам или параллелям. В них искажения длин отсутствуют по одному из направлений: либо вдоль меридиана, либо вдоль параллели.
Для навигации используются равноугольные проекции, для территориального планирования равновеликие и равнопромежуточные.
Произвольные. На карте в любых соотношениях имеются искажения и углов, и площадей. Но эти искажения распределяются по карте наиболее выигрышным образом, при этом достигается некий компромисс. Например, минимальные искажения приходятся на центральную часть карты, а все сжатия и растяжения «сбрасываются» к её краям.
Факторы выбора картографических проекций.
— Географические особенности территории. Ее положение на Земном шаре, размеры, широтная или меридиональная конфигурация.
— Назначение, масштаб и тематика карты.
— Условия и способы использования карты, задачи, которые будут по ней решаться, требование к точности.
— Особенности самой проекции. Искажения и.т.д.
Значимость факторов может быть различна в зависимости от назначения карты. Так для навигационных важна точность, для школьной карты – наглядность, а для карты Арктики – положение на Земном шаре.
Дата добавления: 2019-02-12 ; просмотров: 172 ; Мы поможем в написании вашей работы!
Для чего используется цилиндрическая проекция
Поверхность земли имеет сферическую форму, поэтому приходится каким-то образом изображать реальный мир в плоской, или планарной системе координат. При создании карт эллипсоид вращения должен быть развернут на плоскость. Понятно, что он не может быть развернут на плоскости без складок или разрывов, поэтому при создании карт прибегают к помощи картографических проекций, в которых отображение поверхности земли или иного небесного тела происходит по строгим математическим законам. Эти законы выражают функциональную связь координат точек на поверхности эллипсоида вращения и плоскости (карте). В основу такого отображения положена система географических или геодезических координат, координатными линиями которой являются меридианы и параллели.
Различные проекции имеют разные типы искажений. Некоторые проекции разработаны с учетом минимизации искажений одной или двух характеристик данных. Проекция может сохранять площадь объектов, но изменять их форму. Растяжение и сжатие отдельных частей изображения картографируемой поверхности в той или иной проекции неизбежно сопровождается искажениями длин, площадей и углов. В одних проекциях можно избежать искажения углов, в других – площадей, но длины линий будут искажены во всех проекциях, за исключением отдельных точек или некоторых линий на карте, о чем мы поговорим несколько позже.
Картографические проекции предназначены для определенных целей, так некоторые картографические проекции могут использоваться для отображения крупномасштабных объектов на ограниченной площади, другие – для составления мелкомасштабных карт мира.
Проекции классифицируются по следующим основным признакам:
по характеру искажений;
по виду нормальной сетки параллелей и меридианов;
по ориентировке вспомогательной поверхности.
По характеру искажений различают проекции:
Среди них особое место занимают проекции равнопромежуточные, в которых масштаб длин по одному из главных направлений сохраняется постоянным.
По по виду нормальной сетки параллелей и меридианов различают проекции:
Рисунок 27. Коническая проекция
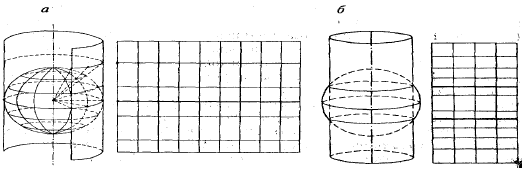
Цилиндрические проекции бывают прямые, косые и поперечные. В прямых цилиндрических проекциях одни и те же участки поверхности изображаются одинаково вдоль линии разреза в восточной и западной частях карты, что обеспечивает удобство чтения карты по широтным поясам. Косые цилиндрические проекции имеют географическую сетку, которая дает представление о сферичности земного шара. С уменьшением широты полюса кривизна параллелей увеличивается, а их протяженность уменьшается, что дает представление о сферичности земли.
Цилиндрические проекции применяются при составлении карт мелких и крупных масштабов — от общегеографических до специальных. Так, например, аэронавигационные маршрутные полетные карты чаще всего составляются в косых и поперечных цилиндрических равноугольных проекциях (на шаре).
Рисунок 28. Цилиндрическая проекция
Рисунок 29. Азимутальная проекция
Применяются прямые, косые и поперечные азимутальные проекции, что определяется широтой центральной точки проекции, выбор которой зависит от расположения территории. Меридианы и параллели в косых и поперечных проекциях изображаются кривыми линиями, за исключением среднего меридиана, на котором находится центральная точка проекции. В поперечных проекциях прямой изображается также экватор: он является второй осью симметрии.
цилиндрическая проекция
Смотреть что такое «цилиндрическая проекция» в других словарях:
цилиндрическая проекция — cilindrinė projekcija statusas T sritis fizika atitikmenys: angl. cylindrical projection vok. Zylinderprojektion, f; zylindrische Projektion, f rus. цилиндрическая проекция, f pranc. projection cylindrique, f … Fizikos terminų žodynas
ЦИЛИНДРИЧЕСКАЯ ПРОЕКЦИЯ — картографическая проекция, в которой параллели нормальной сетки параллельные прямые, а меридианы перпендикулярные параллелям прямые; расстояния между ними пропорциональны разностям долгот. Большая часть морских карт составлена в Цилиндрической… … Морской энциклопедический справочник
Цилиндрическая проекция — один из видов картографических проекции (См. Картографические проекции) … Большая советская энциклопедия
Цилиндрическая проекция Миллера — Проекция Миллера для Земного шара Цилиндрическая проекция Миллера модификация проекции Меркатора, предложенная … Википедия
Эквидистантная цилиндрическая проекция — The Blue Marble: Land Surface, Ocean Color and Sea Ice как пример равнопромежуточной проекции Равнопромежуточная проекция одна из основных картографических проекций. Она, как и проекция Меркатора, относится к цилиндрическим проекциям. При этой… … Википедия
цилиндрическая картографическая проекция — цилиндрическая проекция Картографическая проекция, в которой параллели нормальной сетки параллельные прямые, а меридианы перпендикулярные параллелям прямые, расстояния между которыми пропорциональны разностям долгот. [ГОСТ 21667 76] Тематики… … Справочник технического переводчика
Проекция Меркатора — Карта мира Меркатора 1569 года Равноугольная цилиндрическая проекция Меркатора одна из основных картографических проекций. Разработана Герардом Меркатором для применения в его «Атласе». «Равноугольная» в названии проекции подчёркивает то, что… … Википедия
Проекция (картография) — Пример картографической проекции проекция Меркатора Картографическая проекция математически определенный способ отображения поверхности эллипсоида на плоскости. Суть проекций связана с тем, что фигуру Земли эллипсоид, не развертываемый в… … Википедия
Проекция Хобо-Дайера — карты мира … Википедия
Цилиндрические проекции
Цилиндрические проекции получаются путем проектирования поверхности глобуса на боковую поверхность касательного или секущего цилиндра. В зависимости от положения оси цилиндра относительно оси вращения Земли цилиндрические проекции могут быть:
1) нормальные — ось цилиндра совпадает с осью вращения Земли;
2) поперечные — ось цилиндра перпендикулярна к оси вращения Земли;
Карты в цилиндрической проекции издаются в нескольких разновидностях.
Нормальная равноугольная цилиндрическая проекцияприобрела всеобщее распространение для составления морских карт. Эту проекцию называют еще проекцией Меркаторапо имени голландского картографа, который ее предложил.
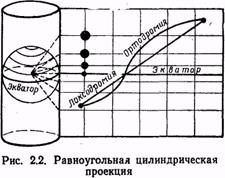
Построение этой проекции производится проектированием глобуса из его центра на боковую поверхность цилиндра, касательного к экватору (рис. 2.2). После проектирования цилиндр разрезается по образующей и разворачивается на плоскость. При проектировании на поверхность цилиндра параллели растягиваются до длины экватора. Соответственно на такую же величину растягиваются и меридианы. Поэтому проекция сохраняет подобие фигур и является равноугольной.
Карты в равноугольной цилиндрической проекции имеют следующие основные свойства:
1) меридианы и параллели изображаются взаимно перпендикулярными линиями;
2) расстояния между меридианами одинаковые, а между параллелями увеличиваются с увеличением широты;
3) сохраняется равенство углов и подобие фигур;
4) масштаб переменный и с увеличением широты становится крупнее, поэтому расстояние между двумя точками определяется по специальной шкале, нанесенной на боковых обрезах карты. Эта шкала учитывает переменный масштаб по широте;
5) искажение масштаба практически не ощутимо только в полосе ±5° от экватора;
6) локсодромия изображается прямой линией, что является основным преимуществом этой проекции, значительно облегчающим решение навигационных задач;
7) ортодромия изображается кривой линией, выпуклой к полюсу (т. е. в сторону более крупного масштаба).
В нормальной равноугольной цилиндрической проекции издаются навигационные морские карты.
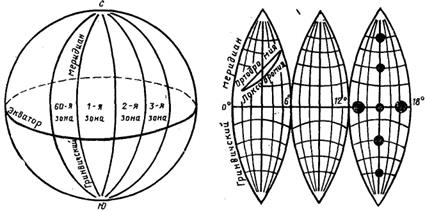
Равноугольная поперечно-цилиндрическая проекция.Эту проекцию предложил немецкий математик Гаусс, поэтому ее обычно называют проекцией Гаусса. Равноугольная поперечноцилиндрическая проекция получается путем проектирования земной поверхности на боковую поверхность цилиндра, расположенного перпендикулярно оси вращения Земли.
Для построения карт в этой проекции поверхность Земли делят меридианами на 60 зон. Каждая такая зона по долготе занимает 6°. Счет зон ведется на восток от Гринвичского меридиана, который является западной границей первой зоны (рис. 2.3). По широте зоны простираются от Северного полюса до Южного. Каждая зона изображается на своем цилиндре, касающемся поверхности глобуса по среднему меридиану данной зоны. Указанные особенности построения позволяют уменьшить искажения.
Карты в равноугольной поперечно-цилиндрической проекции имеют такие свойства:
1) незначительное искажение масштаба; на осевых меридианах искажения длин отсутствуют, а по краям зон на широте 0° не превышают 0,14%, т. е. 140 м на 100 км измеряемой длины и практического значения не имеют;
2) сохраняется равенство углов и подобие фигур; на крайних меридианах зон фигуры изображаются в более крупном масштабе, чем на среднем меридиане;
3) осевой меридиан зоны и экватор изображаются прямыми взаимно перпендикулярными линиями; остальные меридианы — кривыми линиями, сходящимися от экватора к полюсам, а параллели— дугами, выпуклыми к экватору; кривизна меридианов в пределах одного листа карты незаметна;
4) в пределах одной зоны листы карт склеиваются без разрывов;
5) локсодромия имеет вид кривой, выпуклой к экватору;
6) ортодромия на расстоянии до 1000 км изображается прямой линией;
7) на картах масштаба 1:200000 и крупнее нанесена километровая
Рис. 2.3. Поперечно-цилиндрическая проекция
сетка прямоугольных координат Гаусса.
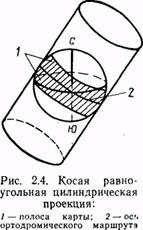
Косая равноугольная цилиндрическая проекция.Эта проекция получается при проектировании земной поверхности на боковую поверхность цилиндра, расположенного под углом к оси вращения Земли (рис. 2.4). Цилиндр располагают так, чтобы он касался глобуса по оси маршрута. Этим достигается уменьшение искажений на составляемой карте. На картах в этой проекции в полосе 500—600 км от осевой линии маршрута искажения масштаба не
превышают 0,5%. Ортодромия в полосе карты изображается прямой линией.
В косой равноугольной цилиндрической проекции издаются маршрутно-полетные карты масштабов 1 : 1 000 000 и 1 : 2 000 000, а также бортовая карта масштаба 1 : 4 000 000.
Дата добавления: 2015-04-21 ; просмотров: 3576 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Цилиндрическая проекция: характеристики, достоинства и недостатки
Содержание:
Однако проекционные цилиндры также могут быть выбраны секущими к двум параллелям, равноудаленным от экваториальной линии, в этом случае цилиндр будет иметь радиус меньше экваториального.
Полученная карта цилиндрической проекции будет представлять собой сетку горизонтальных параллелей и вертикальных меридианов, образующих прямые углы.
Преимущества цилиндрической проекции
В картографии используется несколько типов цилиндрических проекций, каждый из которых имеет свои сильные и слабые стороны. В любом случае выбор типа проекции будет зависеть от конечного назначения карты.
Прежде всего, преимущество этой и любой другой картографической проекции состоит в том, что с их помощью вы можете визуализировать части Земли на плоской поверхности и брать их с собой для удобства.
Цилиндрическая проекция очень подходит для карт мира, поскольку могут быть представлены оба полушария, в отличие от других проекций, таких как коническая проекция, которая позволяет отображать только одно из полушарий.
Теперь при изображении сферической поверхности на плоскости она всегда будет так или иначе искажена. В случае цилиндрической проекции наименьшие искажения возникают в тропической зоне.
Именно для того, чтобы воспользоваться преимуществами этого типа проекции, но в то же время, пытаясь минимизировать эти неудобства, географы на протяжении веков предлагали различные типы цилиндрических проекций.
Цилиндрическая проекция Меркатора
Изобретение этой проекции приписывается бельгийскому картографу, географу и математику Герарду Меркатору в 1569 году. Это одна из наиболее широко используемых проекций на картах мира даже сегодня.
Его главное достоинство в том, что маршрут с постоянным направлением отображается на карте прямой линией.
Из-за этой уникальной особенности навигаторы переняли именно этот тип карты вскоре после ее выпуска. В этом случае проекция соответствует проекции, поскольку сохраняет направления и углы.
Но именно это делает проекцию Меркатора не сохраняющей площади.Регионы за пределами тропиков, особенно далеко на севере или далеко на юге, выглядят чрезмерно большими.
С момента своего создания проекция Меркатора широко использовалась для отображения карт мира с континентами и странами.
Недостатки
Проблема с цилиндрической проекцией, как мы видели в предыдущих разделах, заключается в том, что шкала искажена в сторону от экватора или опорных параллелей, также известных как стандартные параллели.
Главный недостаток заключается в том, что за пределами тропических регионов это искажение форм и расстояний увеличивается, увеличивая эту деформацию для полярных широт, из-за чего эти территории кажутся намного больше, чем они есть на самом деле.
По этой причине были внесены модификации для максимального устранения искажений, появляющиеся варианты в цилиндрических выступах, основные характеристики которых представлены ниже.
Это вариант классической проекции Меркатора, которая стала стандартной картографической системой для Интернета. Это система, принятая Google в 2005 году для своих популярных приложений, Google Maps и Google Earth.
Другие крупные поставщики карт в Интернете, такие как Bing Maps, Mapquest, OpenStreetMap, Mapbox и другие, приняли эту систему проецирования.
Разница между исходной проекцией Меркатора и проекцией этого типа очень тонкая, и конечный результат очень мало отличается.
В исходной проекции Земля предполагается сферой, тогда как в сети Меркатор Земля считается эллипсоидальной.
Однако есть страны, которые не внедрили эти улучшения в свои карты. Например, для континентальной части Соединенных Штатов и Канады проекция конической формы Ламберта предпочтительна для аэронавигационных карт и проекция Альберта Коника для данных кадастра.
Цилиндрическая проекция Ламберта
Это цилиндрическая проекция, предложенная в 1772 году швейцарским математиком и географом Иоганном Генрихом Ламбертом (1728-1777). В своей первоначальной версии Ламберт использует экватор как опорную параллель.
В этом типе проекции цель состоит в том, чтобы исправить искажение в области, вызванное проекцией Меркатора, поэтому она также известна как цилиндрическая проекция равной площади.
Постоянство площади в проекции Ламберта достигается за счет деформации ракурса, главным образом в областях больших значений широты.
На основе этого типа проекции возникло семейство по крайней мере из семи вариантов, в которых выбраны две параллели, равноудаленные от экваториальной линии, сохраняя неизменность области как фундаментальную характеристику, но минимизируя деформацию в интересующих широтах. согласно использованию карты.
Другие виды цилиндрических выступов, их достоинства и недостатки
Помимо уже рассмотренных, есть и другие виды цилиндрических выступов, даже довольно старые. Некоторые из них описаны ниже.
Эквидистантная цилиндрическая проекция
Это тип простой проекции, в которой меридианы земной сферы превращаются в равноотстоящие вертикальные линии. Аналогичным образом параллели или круги широты становятся горизонтальными линиями, которые также находятся на одинаковом расстоянии.
Этот тип проекции очень древний и приписывается Маринусу Тириосскому, греческому географу, который жил между 70 и 130 годами нашей эры. С.
Этот тип проекции имеет недостаток, заключающийся в том, что он деформирует области и формы, главным образом, в зонах более высоких широт, чем тропики, сглаживая формы по горизонтали вблизи полярных регионов.
Таким образом, этот тип проекции не сохраняет площади и углы, за исключением экваториальной параллели, где это точно.
Цилиндрическая проекция Миллера
Он был предложен картографом Осборном Мейтландом Миллером (1897–1979) в 1942 году с использованием экватора в качестве эталона, параллельного цилиндру проекции.
Эта проекция очень похожа на проекцию Меркатора, но с тем недостатком, что она не соответствует требованиям, то есть фиксированный курс на карте Миллера выглядит как кривая.
Чтобы выполнить свою проекцию, Миллер начал с проекции Меркатора, умножив реальную широту на коэффициент, а затем выполнил проекцию Меркатора. Чтобы компенсировать коэффициент на прогнозируемой широте, он умножается на обратный коэффициент, то есть 5/4.
В результате формы в высоких широтах меньше искажаются по сравнению с исходной формой.
Ссылки
Теорема о факторах: объяснение, примеры, упражнения
Отказ от ответственности: что это такое и как это сделать