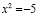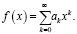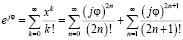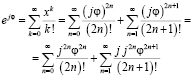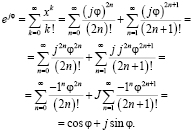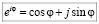Для чего используют комплексные числа

Введение в комлексные числа

Выяснив, что многие знакомые программисты не помнят комплексные числа или помнят их очень плохо, я решил сделать небольшую шпаргалку по формулам.

А школьники могут что-то новое узнать 😉
// Всех кого заинтересовал прошу под кат.

Итак, комплексные числа эта такие числа, которые можно записать как

Где x, y вещественные числа(т.е привычные всем числа), а i — число, для которого
выполняется равенство

x называется действительной частью, y — мнимой.

Это алгебраическая форма записи комплексного числа.

Существует также тригонометрическая форма записи комплексного числа z:

С введением, пожалуй, все.

Переходим к самому интересному — операциям над комплексными числами!
Для начала рассмотрим сложение.

У нас есть два таких комплексных числа:

Как же их сложить?
Очень просто: сложить действительную и мнимую части.
Получим число:

Все просто, не так ли?
Вычитание выполняется аналогично сложению.
Нужно просто вычесть из действительной части 1 числа действительную часть 2 числа,
а потом проделать тоже с мнимой частью.
Получим число

Умножение выполняется вот так:

Напомню, x это действительная часть, y — мнимая.
Деление выполняется вот так:

Кстати, поддержка комплексных чисел есть в стандартной библиотеке Python:

Вместо i используется j.
Кстати, это потому что Python принял конвенцию инженеров-электриков, у которых
буква i обозначает электрический ток.
Задавайте свой вопросы, если они есть, в комментариях.
Надеюсь, вы узнали для себя что-то новое.

UPD: В комментариях просили рассказать о практическом применении.
Так вот комплексные числа нашли широкое практическое применение в авиации
(подъемная сила крыла) и в электричестве.
Как видете, очень нужная вещь 😉

Источник

Комплексные числа

Формы

Так сложилось в математике, что у данных чисел несколько форм. Число одно и тоже, но записать его можно по-разному:

Далее с примерами решений вы узнаете как переводить комплексные числа из одной формы в другую путем несложных действий в обе стороны.

Изображение

Изучение выше мы начали с алгебраической формы. Так как она является основополагающей. Чтобы было понятно в этой же форме изобразим комплексное число на плоскости:

Вычислить сумму и разность заданных комплексных чисел:

Сначала выполним сложение. Для этого просуммируем соответствующие мнимые и вещественные части комплексных чисел:

Аналогично выполним вычитание чисел:

Выполнить умножение и деление комплексных чисел:

Так, теперь разделим первое число на второе:

Суть деления в том, чтобы избавиться от комплексного числа в знаменателе. Для этого нужно домножить числитель и знаменатель дроби на комплексно-сопряженное число к знаменателю и затем раскрываем все скобки:

Разделим числитель на 29, чтобы записать дробь в виде алгебраической формы:

Для возведения в квадрат достаточно умножить число само на себя:

Пользуемся формулой для умножения, раскрываем скобки и приводим подобные:

В этом случае не всё так просто как в предыдущем случае, когда было возведение в квадрат. Конечно, можно прибегнуть к способу озвученному ранее и умножить число само на себя 7 раз, но это будет очень долгое и длинное решение. Гораздо проще будет воспользоваться формулой Муавра. Но она работает с числами в тригонометрической форме, а число задано в алгебраической. Значит, прежде переведем из одной формы в другую.

Вычисляем значение модуля:

Найдем чем равен аргумент:

$$ \varphi = arctg \frac<3> <3>= arctg(1) = \frac<\pi> <4>$$

Записываем в тригонометрическом виде:

Преобразуем в алгебраическую форму для наглядности:

Представим число в тригонометрической форме. Найдем модуль и аргумент:

Используем знакомую формулу Муавра для вычисления корней любой степени:

Источник

Для чего используют комплексные числа

В математике чрезвычайно обширно используется решение задач с помощью комплексных чисел. Однако, что такое комплексные числа и как они нашли себя в электротехнике [4]?

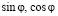
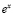
Для начала рассмотрим формулу Эйлера. Это серьёзная и важная формула, которая объединяет тригонометрические функции с экспонентой – с функцией, которая не входит в состав периодических функций, но очень часто используется в электротехнике [1].

Формула Эйлера считается базовой формулой при вычислении комплексных напряжений токов в электротехнике [2 ].

Известно, что свойства большинства математических функций выводят на множестве вещественных чисел, если они на этом множестве существуют. Но, например, уравнение

решения в области вещественных чисел не имеет.

Для того чтобы обеспечить решение таких уравнений, было введено понятие комплексного числа, включающего в себя не только вещественную, но и мнимую часть, которая содержит мнимую единицу, по определению равную

.

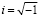
Если ввести допущение, что такое число существует, то всё равно очень много математических функций при невыполнении не выводят за множество комплексных чисел, а продолжают рассматривать на множестве вещественных чисел. При этом остаётся немало задач, особенно прикладного характера, решение которых нужно производить с помощью комплексных чисел [5, 6, 8].

Комплексным числом Z в общем случае считают сумму пары чисел – вещественного числа x и произведения yi, где i – есть мнимая часть:

.

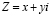
Преимуществом комплексных чисел является то, что, практически, все математические операции над комплексными числами не выходят за множество комплексных чисел, то есть результат действия над комплексными числами можно выразить в виде комплексного числа.

Этим активно пользуются при расчётах в электротехнике. В математике для символического изображения мнимой единицы используют обозначение i, но в электротехнике же так принято обозначать ток, поэтому это обозначение заменяют на j, физический смысл же от этого не меняется:

.

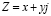
Вернёмся, применив эту формулу к тригонометрическим функциям, а именно к .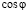

Учтём, что любая функция f(x) при определённых условиях представима в виде степенного ряда, то есть сводится к виду

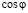
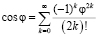
При разложении функции в ряд Маклорена получим:

.

Также распишем ряд Маклорена для функции :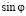

.

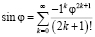
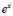
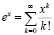
Точно так разложим на ряд Маклорена функцию и получим:

.

Предположим, что х принадлежит множеству комплексных чисел и 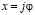. Для того, чтобы получить формулу Эйлера разобьём этот ряд на два ряда по чётным и нечётным степеням k:

далее в первом и втором слагаемом путём элементарных преобразований вынесем за скобку 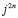и получим:

Учитывая то, что 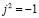, то получим следующее:

Собственно говоря, мы получили формулу Эйлера, устанавливающую зависимость между экспонентой и тригонометрическими функциями и имеющую вид:

Эта формула существенно помогает упростить математические выражения в комплексной области. Так при описании электромагнитных процессов в цепях переменного тока приходится вычислять много непростых интегралов, что приводит к громоздкому решению. Оказалось, что выполнение поставленных задач упрощается при введении комплексных чисел [3, 7].

Комплексные числа можно представлять в разных формах записи – алгебраической, тригонометрической или показательной – в зависимости от постановки задачи, исходных данных и требуемых результатов, но благодаря формуле Эйлера легко переходить от одной формы записи к другой. Например, переменный ток в цепи можно записать по-разному:

– алгебраическая форма;

= – тригонометрическая форма;

= – показательная форма.

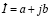
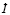
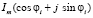
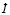
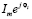
При сложении токов в цепях с начальной фазой, равной нулю, сложностей не возникает. Но при сложении токов с разными начальными фазами простая, на первый взгляд, задача приводит к громоздким тригонометрическим вычислениям. Тогда как, используя переход к комплексным числам, эта же задача решается в несколько строк [9, 10].

Если решать задачи электротехники с помощью векторов, то опять же удобно перейти к комплексной записи токов или напряжений и выполнять построения на комплексной плоскости, где горизонтальная ось – ось вещественной части комплексного числа, а вертикальная – ось мнимой части этого же числа.

Комплексные числа также применяются для описания гармонических колебаний в линейных электрических цепях, при этом переход от реальных гармонических токов и напряжений к комплексным амплитудам выражает суть метода комплексных амплитуд, который является моделью исследуемых процессов, где на первое место выдвигаются амплитуды, а время и частоты отодвигаются на задний план. Переход к комплексным значениям позволяет компактно описать один объект сразу двумя величинами.

По сути, переход от реальных гармонических колебаний к комплексным амплитудам есть построение модели с помощью комплексных чисел, которые в этой модели носят названия – комплексный ток, комплексное напряжение, комплексная ЭДС.

Применение комплексных чисел позволяет:

– использовать законы, формулы и методы расчётов, применяющиеся в цепях постоянного тока, для расчёта цепей переменного тока;

– упростить некоторые вычисления, заменив графическое решение с использованием векторов на алгебраическое решение;

– рассчитывать сложные цепи, не решающиеся другим путем;

– упростить расчеты цепей постоянного и переменного токов.

Источник

Основные действия над комплексными числами

Комплексные числа — определение и основные понятия

Обычные числа представляют собой множество действительных чисел, для обозначения которых используют букву R. Каждое число из множества можно отметить на числовой прямой.

К действительным числам носят:

Каждая точка на числовой прямой характеризуется некоторым действительным числом. Комплексное число является двумерным числом и записано в виде:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Где а и b являются действительными числами, i представляет собой так называемую мнимую единицу.

Уравнение можно мысленно поделить на несколько частей:

Следует отметить, что a + bi является единым числом, а не сложением. Места действительной и мнимой частей в уравнении можно менять:

Мнимую единицу допускается переставлять:

При таких операциях смысл выражения остается прежним. Однако стандартная запись комплексного числа имеет такой вид:

Данное утверждение можно привести в виде геометрической интерпретации. Тогда комплексные числа изображают на комплексной плоскости.

С помощью R обозначаю множество действительных чисел. В случае, когда требуется обозначить множество комплексных чисел, принято использовать букву С. Наличие буквы С на чертеже говорит о том, что на нем представлена комплексная плоскость. Данная плоскость включает две оси:

Re z — является действительной осью;

Im z — представляет собой мнимую ось.

Правила оформления такого графика практически не отличаются от требований к чертежам для декартовой системы координат. По осям задают масштаб и отмечают:

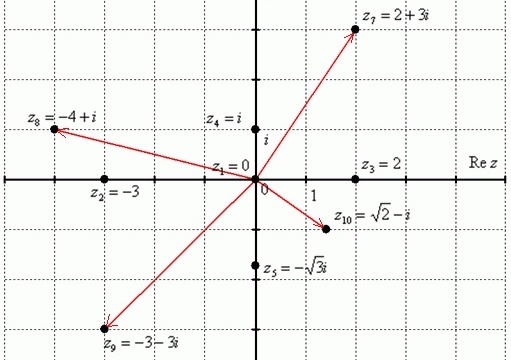
С помощью комплексной плоскости можно построить заданные комплексные числа:

Можно рассмотреть следующие комплексные числа:

Действительные числа являются частным случаем комплексных чисел. Действительная ось Re z обозначает в точности множество действительных чисел R, то есть на данной оси расположены все числа с обычными свойствами. Можно сформулировать справедливое утверждение: множество действительных чисел R представляет собой подмножество множества комплексных чисел С.

Данные числа являются комплексными числами, мнимая часть которых нулевая:

Мнимые числа с нулевой действительностью, которые расположены на мнимой оси Im z:

Есть ряд чисел с ненулевыми действительной и мнимой частью:

Для их обозначения используют точки на комплексной плоскости. К таким точкам проводят радиус-векторы из начала координат. Радиус-векторы не принято чертить к числам, которые расположены на осях и сливаются с ними.

Формы, как записываются

Алгебраическая запись комплексного числа имеет такой вид:

Кроме данной формы существует еще несколько способов для записи. Удобным и наглядным геометрическим представлением является:

z = a + bi в виде вектора с координатами (а;b) на декартовой плоскости, либо точкой — концом вектора с аналогичными координатами.

В этом случае пару комплексных чисел представляют в виде суммы соответствующих векторов, которую рассчитывают с помощью правила параллелограмма. Согласно теореме Пифагора, длина вектора с координатами (а;b) определяется, как:

Данная величина представляет собой модуль комплексного числа z = a + bi и имеет такое решение:

Вектор и положительное направление оси абсцисс образуют угол, отсчитанный против часовой стрелки. Данный угол называют аргументом комплексного числа z и обозначают, как Arg z. Аргумент имеет неоднозначное определение с точностью до прибавления величины, которая кратна 2π радиан. При повороте на такой угол вокруг начала координат вектор не изменяется.

В том случае, когда вектор длиной r с положительным направлением оси абсцисс составляет угол ϕ, его координаты будут следующими:

\(\left(r*\cos \varphi ;r*\sin \varphi \right)\)

Таким образом, получают тригонометрическую форму записи комплексного числа:

\(z=\left|z \right|*\left(\cos (Arg z)+i\sin (Arg z) \right)\)

Из-за более простого вида вкладок комплексные числа, как правило, представляют в тригонометрической форме.

Существует показательная форма для записи комплексных чисел. Какое-либо комплексное число, не равное нулю, можно представить в показательной форме:

Где \(\left|z \right|\) является модулем комплексного числа,

\(\varphi\) представляет собой аргумент комплексного числа.

Представить комплексное число в показательной форме можно с помощью нескольких действий:

Основные действия над комплексными числами с примерами

Манипуляции с комплексными числами выполняют так же, как с действительными числами. Арифметические действия могут быть следующими:

Складывать и вычитать комплексные числа можно с помощью правила:

(a + bi) ± (c + di) = (a ± c) + (b ± d)i

Умножение комплексных чисел выполняют таким образом:

(a + bi) · (c + di) = (ac – bd) + (ad + bc)i

В данном случае \(i^<2>=-1\)

Число \(\bar=a-bi\) является комплексно-сопряженным к \(z=a+bi\)

С помощью равенства \(z*\bar=a^<2>+b^<2>\) можно установить, как делить одно комплексное число на другое, не равное нулю, комплексное число:

Сложение комплексных чисел

Ели требуется сложить пару комплексных чисел:

Сначала нужно найти сумму их действительных и мнимых частей:

Таким образом, сумма какого-либо количества слагаемых определяется путем сложения действительных частей и сложением мнимых частей. В случае комплексных чисел справедливо правило первого класса, которое гласит, что от перестановки слагаемых их сумма остается прежней:

Вычитание комплексных чисел

Разность комплексных чисел:

Действие аналогично сложению. Разница заключается в необходимости выделения скобками вычитаемого числа. Далее следует раскрыть скобки и изменить знак:

Полученное в результате число обладает двумя частями. Действительная часть является составной:

Наглядно ответ будет записан в такой форме:

Умножение комплексных чисел

Можно найти произведение комплексных чисел:

Произведение будет записано таким образом:

Раскрыть скобки следует, руководствуясь правилом умножения многочленов, учитывая, что \(i^<2>=-1\)

Для того чтобы перемножить многочлены, требуется каждый член одного многочлена умножить на каждый член другого многочлена. Таким образом:

Как и в случае со сложением, произведение комплексных чисел перестановочно, то есть справедливо равенство:

Деление комплексных чисел

На примере комплексных чисел:

требуется определить частное:

Частное будет записано в таком виде:

Делить числа необходимо с помощью метода умножения знаменателя и числителя на сопряженное знаменателю выражение. В этом случае пригодится стандартная формула:

По условию знаменатель 7-6i. В данном знаменателе уже есть (а-b), поэтому сопряженным выражением в таком случае является (a+b), то есть 7+6i. Исходя из правила, знаменатель умножают на 7+6i. Сохранить равенство можно с помощью умножения числителя на то же самое число 7+6i:

Затем в числителе необходимо раскрыть скобки, то есть умножить пару чисел, согласно отмеченному ранее правилу. Для знаменателя требуется использовать формулу \((a-b)(a+b)=a^<2>-b^<2>\) и \(i^<2>=-1\)

Уравнение будет записано в таком виде:

Нахождение аргумента

При выполнении действий с модулем комплексных чисел необходимо руководствоваться формулой:

Для поиска аргумента комплексного числа требуется использовать определенную формулу для конкретного случая. Уравнение подбирается, исходя из положения числа z = a + bi в координатной четверти. Существует всего три таких варианта:

Извлечение корня из комплексных чисел

Комплексные числа в тригонометрической форме умножают таким образом:

z_<1>*z_<2>=\left|z_ <1>\right|*\left|z_ <2>\right|*(\cos (Arg z_<1>+Arg z_<2>)+i\sin (Arg z_<1>+Arg z_<2>))2

При умножении пары комплексных чисел их модули перемножаются, а аргументы складываются. Исходя из этого утверждения, вытекают формулы Муавра:

С помощью этого равенства можно извлечь корни любой степени из комплексных чисел. Корень n-й степени из числа z представляет собой комплексное число w, которое:

Где k может обладать любым значением из множества (0, 1, …, n-1).

Таким образом, в любом случае имеется ровно n корней n-ой степени из комплексного числа. На плоскости все они будут расположены в вершинах правильного n-угольника.

Возведение комплексных чисел в степень

В качестве примера можно возвести в квадрат комплексное число:

Первый способ заключается в записи степени в виде произведения множителей:

Далее необходимо перемножить числа, согласно правилу умножения многочленов.

Второй метод заключается в использовании уравнения для сокращенного умножения:

Выражение примет следующий вид:

В случае комплексного числа можно достаточно просто записать определенную формулу для сокращенного умножения:

Такую же формулу можно представить для расчета квадрата разности, куба суммы и куба разности. Если необходимо возвести в 5-ю, 10-ю или любую другую степень комплексное число, следует воспользоваться тригонометрической формой комплексного числа, то есть формулу Муавра. К примеру, дано комплексное число в тригонометрической форме:

\(x = <-b \pm \sqrt\over 2a>z=\left|z \right|*\left(\cos \varphi +i\sin \varphi \right)\)

Данное число требуется возвести в натуральную степень n. Для этого необходимо использовать уравнение:

\(z^=\left|z \right|^*\left(\cos (n\varphi) +i\sin (n\varphi) \right)\)

Представленная формула вытекает из правила для умножения комплексных чисел, которые записаны в тригонометрической форме. Для того чтобы найти произведение чисел, требуется:

\(z_<1>=\left|z_ <1>\right|*(\cos \varphi _<1>+i\sin \varphi _<1>)\)

\(z_<2>=\left|z_ <2>\right|*(\cos \varphi _<2>+i\sin \varphi _<2>)\)

Далее требуется перемножить модули этих комплексных чисел и найти сумму аргументов:

\(x = <-b \pm \sqrt\over 2a>z_<1>* z_<2>=\left|z_ <1>\right|*\left|z_ <2>\right|*(\cos( \varphi _<1>+\varphi _<2>)+i\sin ( \varphi _<1>+\varphi _<2>)\)

Аналогичный порядок действий для показательной формы комплексного числа:

Источник