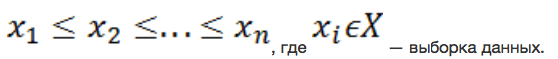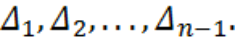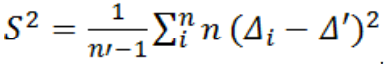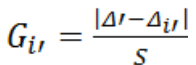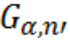Для чего используют критерий граббса

Определение выбросов по критерию Граббса

Существуют стандартные критерии определения выбросов в выборке при заданном уровне значимости/доверия. Примерами таких критериев служат: критерий Шовене, тест Граббса, критерий Пирса, Q-тест Диксона. Упомянутые критерии (за исключением критерия Граббса) выстраивают выборку по возрастанию и проверяют крайние значения (min, max элемент выборки) на выброс, подключается таблица критических значений.

Содержание

Значения в таблицах зависят от количества элементов в выборке и уровня доверия/значимости. Критерии позволяют определить точно один выброс, в случае, когда их много, критерии могут не работать.

Описание подхода

1. Выстраиваем все элементы выборки по возрастанию (от меньшего к большему):

В случае многомерной выборки для сравнения элементов предлагается рассматривать евклидову метрику.

2. Определение максимально возможный процент выбросов в выборке (указывается экспертом, например 5%)

Здесь определяется верхняя граница количества выбросов. Это не значит, что число выбросов будет составлять строго 5% от выборки, это число будет меньше либо равно 5%. Этот параметр обозначим за g.

3. Строим ряд разностей

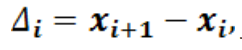
таким образом получим n-1 положительных элементов в последовательности (последовательность не обязательно возрастающая):

4. Находим максимальную разность

В последовательности разностей находим максимальную разность: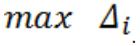

5. Проверка, попадает ли выброс в заданную в п.2. область

В противном случае, элемент с индексом i’ подозрителен на выброс.

6. Вырезаем подвыборку из начального набора данных

Здесь имеем два случая:

7. Среднее значение разностей

Находим среднее значение выборки разностей (п.3.) с учетом набора индексов (п.6.):

– число элементов в вырезанной подвыборке.

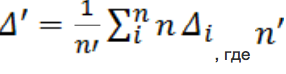
8. Среднеквадратическое отклонение

Рассчитываем характеристику разброса элементов:

9. Считаем статистику Граббса

Используем формулу Граббса для расчета значения статистики:

10. Задаем уровень значимости

– величина вероятности ошибки ( обычно 1%, 5%, 10%).

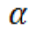
11. Использование таблицы критических значений, сравнение величины статистики из п.9. с критическим значением

По значению уровня значимости и числу элементов в подвыборке n’ находим критическое значение в таблице Граббса, обозначим его за

Сравниваем полученное значение полученное в п.9. Возможны два случая:

– исследуемое значение не является выбросом и в выборке нет начальном наборе данных нет выбросов вообще.

– исследуемое значение является выбросом.

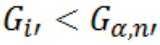
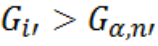
Если оно находится во второй половине выборки (п.1.), то все значения идущие после i ‘ являются выбросами, если оно находится в первой половине выборки (п.1.), то все значения идущие до i’ являются выбросами.

12. Если в п.11. был обнаружен выброс, то из начальной выборки убираем выбросы и повторяем весь алгоритм с первого пункта (п.1.)

Если вы уже используете сервис КОРУС | Управление запасами, но у вас остались вопросы по настройке интерфейса и отчетов, напишите нам на wms@korusconsuting.ru.

Вы можете ознакомиться с функциональностью сервиса и оценить его эффективность на примере собственных данных.

Запросите бесплатный тестовый доступ к сервису и начните оптимизацию запасов прямо сейчас!

Задайте вопрос эксперту на нашем сайте или по телефону: +7 495 130 01 87.

Источник

Аккредитация в Росаккредитации

форум для аккредитованных лабораторий

Точность методов и результатов измерений.

#1 Точность методов и результатов измерений.

Neiron601b, файл распространяется бесплатно и принадлежит домену данного форуму. Разрешается любое использование в т.ч и статистических таблиц. (модификация, копирование, частичное копирование, округление). При копировании и использовании таблиц ссылка на тему Точность методов и результатов измерений. обязательна. Так же желательно указать дату создания и версию таблицы. Расчёты прошли валидацию. Критические значения для критерия Граббса полностью коррелируют с ГОСТ Р ИСО 5725-2-2002 (это подтверждает правильность расчёта, (выбранную модель расчёта) статистических таблиц). Так же был создан отдельный файл для независимой перепроверки правильности расчёта уровней значимости p (значения выбирались случайным образом) Ошибок обнаружено небыло. Файл готов для верификации в аккредитованных лабораториях.

Пароль для защищённых листов 1234
По умолчанию редактировать можно только значения помеченные красным цветом.
При скачивании из интернета файла у меня включился защищённый просмотр, (невозможно вносит данные). Необходимо отключить в настройках Excel. Файл => Сведения => Разрешить редактирование

Реализовано:
Проверка на грубые выбросы.
1. Критерий Граббса одно наибольшее или одно наименьшее значение
2. Критерий Граббса два наибольших или два наименьших значения

#2 Выбросы

Выбросы
В простейшем случае выброс представляет собой наблюдение, несовместимое с остальными наблюдениями набора данных. В общем случае набор данных может содержать более одного выброса, расположенных, как с одной, так и с двух сторон упорядоченного набора данных. Основная проблема выявления выбросов состоит в определении того, действительно ли наблюдения, не совместимые с остальными данными являются выбросами. Эту задачу решают посредством заданного критерия значимости с учетом предполагаемого распределения данных. Наблюдения, для которых получены значимые результаты, рассматривают как выбросы из предполагаемого распределения.

Важность правильного выбора соответствующего распределения данных нельзя переоценить. На практике часто в качестве распределения данных часто рассматривают нормальное распределение, даже если данные получены из другого источника. Однако ошибочное предположение о распределении данных может приводить к некорректному отнесению элементов выборки к выбросам.

Причины выбросов
Появление выбросов обычно связано с одной или несколькими причинами.

a) Ошибки измерений и регистрации данных. Сюда относят ошибки в точности измерений, некорректно проведенные наблюдения, некорректную регистрацию данных или их введения в базу данных.

b) Загрязнение данных. Загрязнение данных происходит в том случае, когда данные принадлежат двум или более распределениям, т. е. имеется одно основное распределение и одно или несколько дополнительных распределений (примесей), загрязняющих данные. Если загрязняющие распределения имеют значительно отличающиеся от основного истинные средние, большие значения стандартных отклонений и/или более тяжелые хвосты распределений, чем у основного распределения, то существует возможность того, что экстремальные наблюдения, принадлежащие распределениям-примесям, могут появиться как выбросы основного распределения.
Примечание 1 — Причиной загрязнения может быть ошибка при отборе выборки, когда небольшую часть данных считают полученной из другой совокупности или если было осуществлено преднамеренное искажение (завышение или занижение) результатов эксперимента или опроса.

c) Ошибочное предположение о распределении данных. Набор данных считают полученным из конкретного распределения, но он получен из другого распределения.
Пример — Набор данных считают отобранным из нормального распределения, но он может иметь сильно ассиметричное распределение (например, экспоненциальное или логнормальное) или быть симметричным, но иметь тяжелые хвосты (например, t-распределение). Поэтому наблюдения, далеко отстоящие от медианы распределения, могут быть ошибочно приняты за выбросы, даже если это достоверные данные, принадлежащие ассиметричному распределению или распределению с тяжелыми хвостами.

d) Редкие наблюдения. В выборках, отобранных (как предполагается) из заданных распределений маловероятные наблюдения могут появиться в очень редких случаях. Экстремальные наблюдения в этом случае обычно принимают за выбросы, но они не являются выбросами.
Примечание 2 — Если генеральная совокупность имеет симметричное распределение с тяжелыми хвостами, то редко поступающие наблюдения могут приводить к ошибочным предположениям о распределении.

Необходимость обнаружения выбросов
Выбросы не всегда являются «плохими» или «ошибочными» данными. Они могут быть рассмотрены как индикаторы проявления редких явлений, требующих дальнейшего изучения. Например, если выброс вызван исключительно особенностями промышленной обработки, то важное значение имеет изучение причин выброса.

Многие методы статистической обработки данных и многие получаемые статистики чувствительны к наличию выбросов. Например, выборочные среднее и стандартное отклонения могут изменить свои значения при наличии даже одного выброса, что впоследствии может привести к неверным выводам.

#3 Точность методов и результатов измерений.

#4 Термины и определения

Выброс: Элемент маломощного подмножества выборки, существенно отличающийся от остальных элементов выборки.
Примечание 1 — Классификация наблюдения или подмножество выборки как выброс (или выбросы) зависит от выбранной модели генеральной совокупности, из которой отобрана выборка. Выброс не рассматривают как истинный элемент генеральной совокупности.
Примечание 2 — Выброс может появиться из другой генеральной совокупности, быть результатом некорректной регистрации данных или общей ошибкой измерений.
Примечание 3 — Подмножество может содержать одно или несколько наблюдений.

Маскировка: Наличие более одного выброса, затрудняющее обнаружение каждого выброса.

Робастная оценка: Оценка, нечувствительная к небольшим отклонениям от предполагаемой вероятностной модели данных.

Ошибка первого рода: Отклонение нулевой гипотезы, когда она истинна. (выброс есть, но не детектирован)

Ошибка второго рода: не отвергают нулевую гипотезу, когда она ложна. (выброса нет, но детектирован)
Вероятность ложного обнаружения выбросов: Вероятность того, что одно или несколько наблюдений незагрязненной выборки, ошибочно классифицированы как выбросы.

Мощность: это вероятность отклонения нулевой гипотезы, когда она ложна. Мощность критерия можно контролировать, повышать, но тогда вырастает шанс допустить ошибку 2-го рода.

#5 Критерий Граббса, ответ на критику.

Тема по обнаружению выбросов не сложная, но многогранная. Начиная писать одно, ты понимаешь, что перед этим нужно объяснить другое. И так по кругу.
Я наработал довольно много материала для анализа результатов измерений, и хотел уже начинать потихоньку выкладывать результаты, но понял что могу столкнутся с критикой, в этой статье я хочу предварительно осветить некоторые моменты.

Претензия первая.
Табличные значения критерия Граббса, приведённые в ГОСТ Р ИСО 5725-2-2002 и ГОСТ Р 8-736-2011, неверны, а именно: указанные в них уровни значимости завышены в два раза, как это показано, в частности, в [1]. В табл. 4а.1 приведены действительные значения Uтабл, взятые из первоисточника [2] Ими и следует пользоваться. ссылка: https://arhiuch.ru/lab4a.html

Прежде чем ответить на критику, расскажу, как были получены цифры в статье и ГОСТах.
Генерировалась необходимого размера n выборка случайных чисел с нормальным законом распределения.
В первом случае рассчитывался Gвыбор МИНИМАЛЬНОГО ИЛИ МАКСИМАЛЬНОГО значения.
Так повторяется несколько тысяч раз. Полученные Gвыборки записываются, упорядочиваются по возрастанию. Наименьшее Gвыбор число, 5%ов наибольших и будет являться Gтабл для доверительной вероятности p=0,95 для n объёма выборки.

Для ГОСТ
Расчёт происходил так же, за исключением: вместо МИНИМАЛЬНОГО, ИЛИ МАКСИМАЛЬНОГО значения выбиралось значение, при котором будет наибольшее Gвыбор.
В итоге, в первом случае получаем (здесь придется вводить понятия) Односторонний критерий Граббса, во втором Двухсторонний критерий Граббса (у которого как раз уровень значимости завышен в два раза).
Прежде чем предположить, где ВЕРНЕЕ, необходимо уточнить, при оценке выборки на грубые выбросы, поиска сомнительных результатов, необходимо самому выбирать критические уровни. И в первом, и во втором случае значения верны, просто они решают разную задачу. (Не буду писать о принятии нулевой гипотезы). В первом случае, Вы отвечаете на два вопроса: Есть ли вероятность выброса у минимального значения, и Есть ли вероятность выброса у максимального значения. (вероятность в процентах 95, или 99)
Во втором — Есть ли вероятность выброса в выборке значения с наибольшим отклонением от среднего (вероятность в процентах 95, или 99).
Лично для меня, второй вариант для целей метрологии логичнее. Покажите, если есть, сомнительное число.

А теперь, где ВЕРНЕЕ
Если до проведения эксперимента допускается, что различие сравниваемых параметров может быть как положительным, так и отрицательным, то следует использовать двусторонний критерий. Если же есть дополнительная информация, например, из предшествующих экспериментов, на основании которой можно сделать предположение, что один из параметров больше или меньше другого, то используется односторонний критерий. Т. е. если мы заранее не знаем может ли быть выброс, будет он минимальным значением, максимальным, либо вообще находится внутри выборки, необходимо брать двухсторонний, а если мы точно знаем, что с какой-либо стороны не может быть выброса (наверное, и такие варианты существуют), необходимо брать односторонний критерий Граббса.
Граббс мне друг, но ГОСТ дороже.

Претензия вторая
Применения критерия Граббса при анализе результатов испытания с тремя элементами.
Таким образом, проведенный моделирующий эксперимент показал ограниченность применения критерия Граббса для выявления выбросов и квази выбросов при проведении испытаний, когда объем выборки n 3. С одной стороны, чувствительность критерия Граббса недостаточная, а значит могут быть получены такие значения, которые с точки зрения физического смысла являются выбросами, а критерий Граббса их «не чувствует». С другой стороны, при двух одинаковых значениях из трех третье значение в выборке всегда по критерию Граббса будет признаваться выбросом. статья: КОРРЕКТНОСТЬ ПРИМЕНЕНИЯ КРИТЕРИЯ ГРАББСА ПРИ АНАЛИЗЕ РЕЗУЛЬТАТОВ ИСПЫТАНИЯ С ТРЕМЯ ЭЛЕМЕНТАМИ. Системи обробки інформації, 2007, випуск 6 (64) Е.Т. Володарский, И.А. Харченко, В.И. Згуря, М.Е. Молочков

Начну с определения.
Критерий Граббса применяется для оценки на грубые ошибки (промахи) сомнительных значений выборки из случайной величины, имеющей НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ.
Т. е. прежде, чем пользоваться этим критерием необходимо, либо доказать, либо предположить, либо по результатам предыдущих опытов принять то, что у Вас нормальное распределение.
Замечания к статье:
Если в выборке два из трёх одинаковые значения, распределение нормальным не будет.
Если «большая» дискретность, распределение нормальным не будет читайте Почему нормальное распределение не нормальное

Следует так же понимать, что бывают разные типы выборок, и статистические методы в некоторых случаях не будут давать ожидаемые результаты.

Например: не стоит искать выбросы при измерении температуры за окном (нестабильный объект исследования), при взятии проб в поле (у вас могут быть локальные загрязнения). В теоретическом эксперименте, приведенный в статье, данные на мой взгляд неподходящие. В статье не известно, что является в реальных условиях причиной разброса. Если регулятор нагрева (температура действительно может расти, рост величины, это не разброс вокруг величины), то такие данные не подходят для получения случайных величин.
Выбросы — это ошибки, это неправильно полученные данные, а не то, на что указала формула. Если система работала правильно, почему там необходимо их искать?

Немного теории. При 3 n обнаружить выбросы действительно сложно, НЕЗАВИСИМО ОТ ВЫБРАННОГО КРИТЕРИЯ.
Если СКО выборки заранее неизвестно, то 3 n это минимальное количество, при котором можно производить расчёты (для некоторых критериев 4-5). Приведу пример и вероятность того, что число 10 не относится к выборке.
1,0; 4,0; 10,0 p=36%
1,0; 2,0; 4,0; 10,0 p=80%
1,0; 2,0; 3,0; 4,0; 10,0 p=93%
1,0; 2,0; 2,9; 3,0; 4,0; 10,0 p=97% (10 — сомнительное)
1,0; 2,0; 2,9; 3,0; 3,0; 4,0; 10,0 p=99% (10- выброс)
Нам потребовалось 6 измерений, чтобы убедиться, что число, отличавшиеся от среднего более чем на 6σ, может являться грубой ошибкой.

Немного теории.
Минимальная последовательность действий при поиске выбросов:
1. Получаем результаты измерений.
2. Доказываем, принимаем, предполагаем, что распределение нормальное, если нет при расчёте используем робастную оценку.
3 Распределение нормальное
3.1 Проверяем на выбросы. Если есть сомнительное значение, проводим анализ, где могла быть ошибка (например, неправильно записали число, сломался прибор).
3.2 Если находим причину сомнительного значения, исключаем ошибочное число и рассчитываем окончательный результат, если нет, рассчитываем окончательный результат.
4.1 Если обнаружен выброс проводим анализ, где могла быть ошибка. (например, неправильно записали число, сломался прибор).
4.2 Если находим причину выброса, исключаем ошибочное число и рассчитываем окончательный результат. Если нет, при расчёте используем робастную оценку.

Оставим о Нём заметку здесь, мне кажется это будет лучшее что можно сделать.

Источник

Расширение области применения критериев типа Граббса, используемых при отбраковке аномальных измерений

Б.Ю. Лемешко, С.Б. Лемешко

Получены таблицы процентных точек для статистик критериев типа Граббса при проверке на выброс одновременно трех максимальных (трех минимальных) значений и одновременно минимального и максималь­ного значений в выборке. Методами статистического моделирования ис­следованы распре­деле­ния статистик критериев Граббса, используемых в задачах отбраковки аномальных измерений, при отклонениях наблюдае­мого за­кона от нормального.

Ключевые слова : проверка гипотез, аномальные наблюдения, кри­терии Граббса, процентные точки

Widening of the application area of Grubbs’s tests used for screening of outlying observations

B.Yu. Lemeshko, S.B. Lemeshko

The tables of percentage points has been obtained for Grubbs’s test sta­tistics in case of testing for discards of three maximal (or three minimal) val­ues simultaneously or minimal and maximal values simultaneously in a sam­ple. The distributions of Grubbs’s test statistics have been investigated by means of statistical simulation methods in problems of screening of outlying observations in case of non-normal distribution under observation.

Key words : testing hypotheses, outlying observations, Grubbs’s tests, percentage points

В практической деятельности важную роль играют статистические критерии, предна­значенные для выделения аномальных результатов из­мерений (выбросов). Если не исключить выбросы из анализируемых данных, то традиционно приме­няемые классические методы статис­тиче­ского анализа, как правило, не являющиеся робастными, чаще всего при­водят к некорректным выводам.

Результаты измерений, содержащие грубые ошибки обычно бы­вают хорошо заметны и могут быть выделены без применения ста­тисти­ческих методов. Применение статистических методов выяв­ления грубых ошибок целесообразно лишь в сомнительных случаях, когда информация о качестве измерений либо неполна, либо ненадежна [1]. При этом, при­меняя статистические методы, следует отслеживать выполнение тех предположений, в условиях которых корректно их использование.

Большинство существующих критериев отбраковки “подозри­тель­ных” данных опирается на предполо­жение о принадлежности наблю­­дае­мых случайных величин нормальному закону. К такого рода критериям относятся простые критерии Граббса 4, применяемые для проверки на аномальность (для оценки анормальности) выделяющихся результа­тов измерений. Использование именно этих критериев пред­полагает стандарт [5], представляющий собой аутентичный текст со­ответствую­щего международного стандарта ИСО 5725. Статистики кри­терия Граб­бса предусматривают возможность проверки на наличие в выборке либо одного аномального результата измерения (наименьшего или наи­боль­шего), либо двух (двух наименьших в выборке или двух наиболь­ших).

Наш интерес к критериям Граббса был обусловлен предпочтением, отданным этим критериям при реализации стандарта ИСО 5725. В на­стоящей работе мы хотели показать, как изменяются распределения ста­тистик критерия Граббса под влиянием отклонения наблюдае­мого закона от нормального. Это должно дать понимание того, что будет проис­хо­дить с результатами применения критериев при нарушении предполо­же­ний о нормальности. Вторая цель заключалась в реализации возмож­но­сти применения критериев с аналогичными статистиками для проверки еще двух гипо­тез: a ) для проверки на аномальность одновременно од­ного минималь­ного и одного максимального элементов в выборке; b ) для проверки на аномальность либо трех минимальных, либо трех макси­мальных элемен­тов в выборке.

В основе данных исследований лежит методика статистического моделирова­ния, опирающаяся на развиваемое программное обеспечение.

, ( 1)

, (2)

, (3)

. (4)

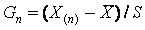
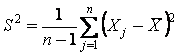
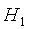
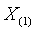
При проверке на выброс наименьшего выборочного значения кон­курирующая гипотеза предполагает, что принадлежит некото­рому другому закону, существенно сдвинутому влево. В данном случае вычисляемая статистика принимает вид

. (5)

Максимальный или минимальный элемент выборки считается вы­бросом, если значение соответствующей статистики превысит крити­че­ское: или , где – задаваемый уровень значимости.

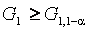
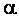
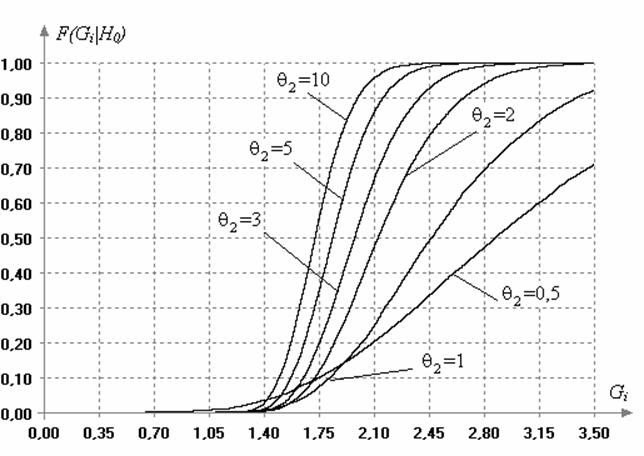
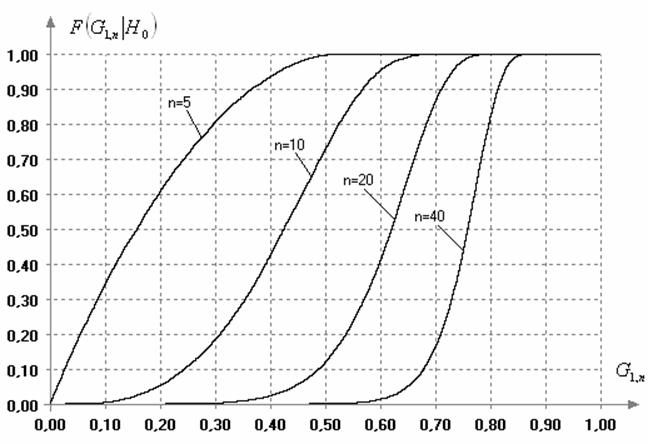
Статистики (1) и (5) распределены одинаково. Вид условных рас­пре­делений 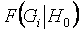статистик (1) и (5) в зависимости от объема анали­зи­руемой выборки при нор­мальном законе наблюдаемых величин пред­ставлен на рис. 1. Распределения статистики существенно зависят от объема выборки . Аналитический вид распределений статистики в стан­дарте [5] и первоисточниках 2 не приводится. Даются лишь верх­ние процентные точки для различных объемов выборок, так как решение об аномальности проверяемого минимального или максимального выбо­рочного значения принимается по правому “хвос­ту” распределения ста­тистики. Если в стандарте процентные точки приведены для объе­мов выборок лишь от 3 до 40, то в [4] процентные точки приведены в диапа­зоне до 147.

Рис. 1. Зависимость распределения статистик (1) и (5) критерия Граббса от объема выборок (в случае нормального закона)

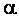
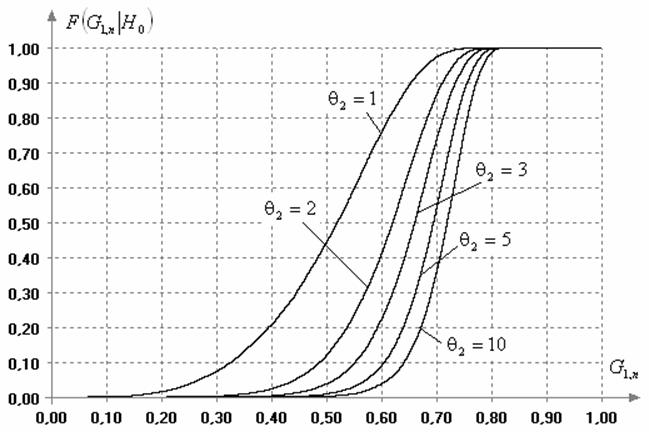
Замечание : В таблице процентных точек, приведенной в стандарте ([5], табл. 5), неверно указаны уровни значимости . На самом деле в данной таблице представлены значения, соответствующие уровням значимости 0.005 (0.5%) и 0.025 (2.5%), а не 0.01 (1%) и 0.05 (5%). Чтобы убедиться в этом, достаточно обратиться к первоисточнику [4]. Данное несоот­вет­ст­вие было замечено в процессе исследований распределений статистик Граббса. Это замечание в силе и для процентных точек статистик, пред­на­значенных для анализа на выбросы одновременно двух мини­мальных или двух максимальных выборочных значений. Вследствие такого недо­разумения при задании уровня значи­мости 0.01 или 0.05 и использовании процентных точек, при­веденных в стандарте ([5], табл.5), ошибочно не будет отбрако­вываться часть выбросов.

Данный критерий можно использовать для выделения аномальных результатов измерений только в случае нормального закона. Если на­блюдаемые слу­чайные величины принадлежат некоторому другому за­кону распределе­ния, то предельное распределение статистик (1) и (5) имеет иной вид. На рис. 2 отражено изменение распределений статистик (1) и (5) в случае принадлежности наблюдаемой случайной величины различным законам экспоненциального семейства распределений с плотностью

. (6)

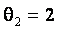
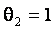
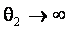
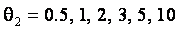
Частными случаями семейства являются нормальный закон при пара­метре формы и распределение Лапласа при . Предель­ными слу­чаями – распределение Коши ( ) и равномерное распределе­ние ( ). На рис. 2 приве­дены распределения статистик (1) и (5) при на­блюдаемых законах (6) со значениями параметра формы и при объемах выборок . Как видим, распределе­ния статистик отличаются очень сильно.

Рис.2. Изменение распределений статистик (1) и (5) критерия Граббса в случае различных законов семейства распределений (6) при

Справедливости ради следует напомнить, что впервые распре­деле­ние статистики вида (1) было исследовано в работе [6]. В [1] приводится целый ряд статистик вида (1) и (5), отличаю­щихся друг от друга комби­нациями известных и оцениваемых параметров сдвига и мас­штаба нор­мального закона. Применение критериев, опирающихся на варианты та­ких статистик, было предусмотрено в [7, 8]. Все приводимые здесь ста­тистики, не смотря на похожесть, отличаются от статистик Граббса (1) и (5), в которых используются оценки обоих параметров нормального за­кона. Вследствие этого и рас­пределения ни одной из этих статистик не совпадает в точности с распределением статистик Граббса (1) и (5). Об­зор еще ряда критериев, предназначенных для выявления и исключения аномальных выбороч­ных значений, приведен в [9].

, (7)

, (8)

, (9)

. (10)

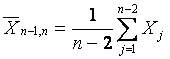
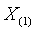
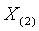
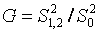
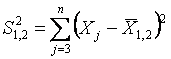
Для проверки на выброс одновременно двух наименьших величин и статистика критерия принимает вид

, (11)

, (12)

. (13)

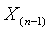
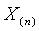
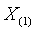
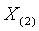
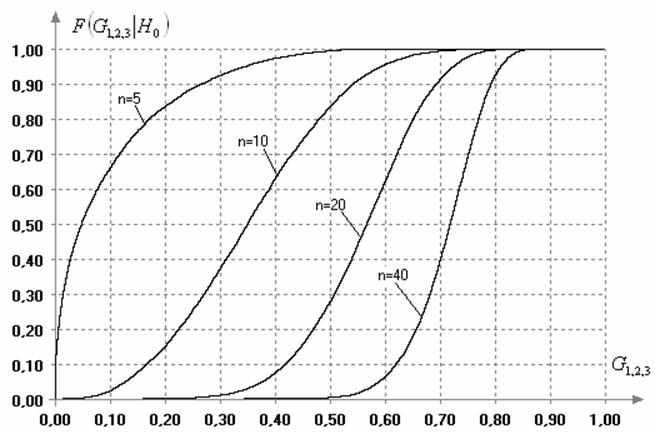
Оба значения ( , или , ) считаются выбросами, если значение соответствующей статистики окажется ниже критического: .

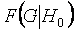
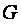
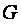
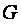
Вид условных распределений статистик (7) и (11) в зави­симости от объема анализируемой выборки представлен на рис. 3. Аналитический вид распределений статистики в стандарте [5] и в 3 не приводится. Даются лишь нижние процентные точки для различных объемов выборок, так как решение об аномальности одновременно двух наименьших или двух наибольших выборочных значений принимается по левому “хвосту” распределения статистики. В стандарте нижние про­центные точки приведены для объемов выборок лишь от 4 до 40. В пер­воисточнике [4] нижние процентные точки распределения статистики приведены в диапазоне до 149.

Рис. 3. Зависимость распределения статистик (7) и (11) критерия Граббса от объема выборок (в случае нормального закона)

Если наблюдаемые случайные величины принадлежат некоторому другому закону, отличному от нормального, то распределения статистик (7) и (11) принимают иной вид. Например, на рис. 4 приведены распреде­ления статистик (7) и (11) при наблюдаемых законах вида (6) со значе­ниями параметра формы при объемах выборок . Как следует из картины, представленной на этом рисунке, распределения статистик Граббса (7) и (11) очень сильно зависят от вида закона, кото­рому принадлежат наблюдаемые величины.

Как и в первом случае, критерий со статистиками (7) – (11) можно применять для отбраковки аномальных наблюдений, используя таблицы процентных точек, приведенные в [5] и в [4], только в случае нормаль­ного закона. Если наблюдаемый закон отличается от нормального, то ис­пользование указанных таблиц, как следует из картин, представленных на рисунках 2 и 4, может приводить как к пропуску выбросов, так и к при­числению к аномальным данных, не являющихся таковыми.

Рис. 4. Изменение распределений статистик (7) и (11) Граббса в случае различных законов распределения при

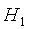
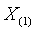
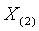
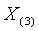
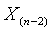
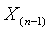
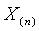
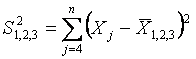
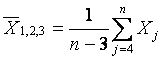
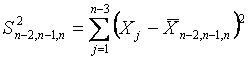
В случае проверки на аномальность одновременно трех минималь­ных или трех максимальных выборочных значений конкурирующая ги­потеза предполагает, что некоторому другому закону принадлежат , и (либо , и ). Статистики для проверки на ано­мальность одновременно трех минимальных или трех максимальных выборочных значений формируются в соответствии с соотношениями:

, (14)

, (15)

, (16)

. (17)

, (18)

. (19)

Статистики (14) и (15) распределены одинаково. Все три измерения считаются выбросами, если значение соответствующей статистики ока­жется ниже критического: или .

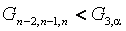
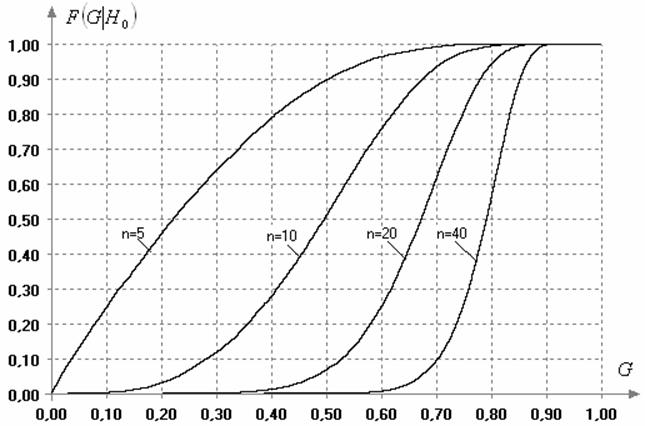
Естественно, что распределения данных статистик также являются зависящими от объема выборок . На рис. 5 показана зависимость от ус­ловных распределений и статистик (14) и (15) в случае извлечения выборок из нормальной генеральной совокупности. Вычисленные с использованием методики статистического моделирова­ния нижние процентные точки ( =0.1%, 0.5%, 1%, 5%, 10%) распределе­ний статистик (14) и (15) при представлены в таблице 1. Про­цент­ные точки стро­ились по моделируемым выборкам статистик. Объем каждой выборки, по которой оценивались процентные точки, составлял 50000 смоде­лиро­ванных значений статистики. В таблице приведены зна­чения процентных точек, полученные усреднением по 15 таким экспери­ментам.

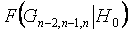
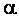
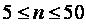
Рис. 5. Зависимость распределения статистик (14) и (15) от объема выборок (в случае нормального закона)

Таблица 1. Нижние процентные точки статистик (14) – (15) критерия типа Граббса

Распределения статистик (14) – (15) также зависят от наблюдае­мого закона. Рис. 6 иллюстрирует поведение распределений данных ста­ти­стик при наблюдаемых законах вида (6) со значениями параметра формы при объемах выборок .

Рис. 6. Изменение распределений статистик (14) и (15) в случае различ­ных законов семейства распределений (6) при

, (20)

, (21)

. (22)

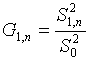
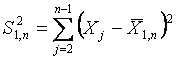
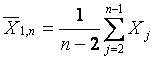
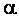
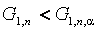
Оба значения считаются выбросами при заданном уровне значимо­сти , если вычисленное по выборке значение статистики (20) окажется ниже критического: .

Вид условных распределений статистики (20) в зависи­мости от объема в случае извлечения анализируемой выборки из нормальной генеральной совокупности представлен на рис. 7. Вычислен­ные с использованием методики статистического моделирования нижние процентные точки распределений статистики (14) при приве­дены в таблице 2.

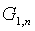
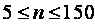
Рис. 7. Зависимость распределения статистики (20) от объема выборки (в случае нормального закона)

Таблица 2. Нижние процентные точки статистик (20) критерия типа Граббса

Распределения статистики (20) существенно зависят от наблюдае­мого закона. Рис. 8 показывает, как меняются распределения данной ста­ти­стики при наблюдаемых законах вида (6) со значениями параметра формы при объемах выборок .

Рис. 8. Изменение распределений статистики (20) в случае различных законов семейства распределений (6) при

Каждый из рассмотренных критериев позволяет (способен) отбра­ковывать содержащиеся в выборке аномальные данные, если количество выбросов в выборке не превышает их числа, на которое рассчитан соот­ветствующий критерий. В тех случаях, когда используемый крите­рий со­ответствует “реальному числу” выбросов, последние, как правило, удается выделить с применением этого критерия. При содержании в выборке большего числа грубых ошибок измерений, чем пред­усматривает стати­стика, критерий уже не способен их выделять. Например, если про­верка на выброс одного наибольшего значения не дала положительного ре­зультата, это еще не означает, что данное значение не является вы­бро­сом. Возможно, что в выборке содержится больше значений, ко­торые могут интерпретироваться как аномальные. Присутствие таких данных отражается на оценках дисперсии (3), (8), и оценках харак­тери­стик рас­сеяния (9), (12), (16), (18), (21), так как все они не явля­ются робастными. Следовательно, при использовании критериев типа Граббса необходимо последовательно тестировать выборку на наличие различного числа гру­бых ошибок измерений.

Выбросы в результатах измерений могут быть вызваны появлением “сдвинутых” значений, связанных с систематической ошибкой, могут быть связаны с увеличением рассеяния результатов измерений в силу различных причин. В последнем случае к выбросам могут относиться как наименьшие, так и наибольшие значения. Способность рассмотренных критериев выделять аномальные результаты измерений будет зависеть от вида за­сорения.

В качестве примера покажем мощность критериев на модели с симметричным засорением, кода выборка из нормальной генеральной совокупности с параметром сдвига и параметром масштаба засо­рена 10% наблюдений нормального закона с параметрами и 5 :

.

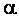
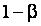
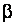
Мощ­ность критерия при заданной вероятности ошибки первого рода опреде­ляется величиной , где – вероятность ошибки второго рода. В данном случае ошибка второго рода заключается в том, что ано­маль­ное значение не идентифицируется как таковое. В таблице 3 приве­дены мощности критериев проверки на аномальность одного минималь­ного (или максимального) значения в выборке, одновременно двух ми­нималь­ных (двух максимальных) значений, одновременно одного мини­маль­ного и одного максимального значений в выборке объемом . Бо­лее высокая в данном случае мощность критерия со статистикой (20) объ­ясняется симметричностью засорения.

Таблица 3. Значения мощности 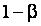критериев типа Граббса по отноше­нию к смеси с 10% симметричным засорением при

Уровень значимости

со статистикой (1) и (5)

со статистикой (7) и (11)

Вообще говоря, в случае необходимости нет принципиальных трудностей для построения модели распределения любой рассмотренной статистики критерия типа Граббса (или для определения процентных то­чек) при любом законе наблюдаемых случайных величин. Проблема лишь в том, что законов, для которых желательно иметь эффективную процедуру отбраковки аномальных измерений, слишком много.

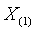
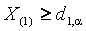
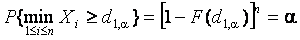
При проверке на выброс наименьшего значения гипотеза при­ни­мается, если . В этом случае , и кри­ти­чес­кое значение опре­деляется из уравнения .

Чтобы с помо­щью данной процедуры корректно выделять содер­жащиеся в выборке грубые ошибки, необходимо знание “истинного” за­кона . Од­нако на практике вектор параметров закона чаще всего прихо­дится оценивать по этой же самой выборке. В связи с чем такую проце­дуру отбраковки иногда называют параметрической. Содержащиеся в выборке выбросы отражаются на оценках параметров закона . Полученный закон ока­зывается существенно отличаю­щимся от “истинного”. Вследст­вие этого параметрические методы от­браковки рез­ко выделяю­щихся наблюдений становятся неустойчивыми [10].

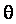
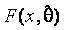
Следует отметить, что подобным же недостатком обладают и кри­терии типа Граббса: нет никакой гарантии, что в выборке не большее число аномальных измерений, чем мы исследуем на выбросы. Тогда это может отрицательно сказаться на результатах анализа.

В параметрических методах отбраковки с данным недостатком бо­рются, применяя робастные методы оценивания, например, оценки мак­симального правдоподобия по группированным данным [11], оптималь­ные L-оценки по выборочным квантилям [12, 13], MD-оценки. Использо­ва­ние робастных методов оцени­вания в процедуре параметрической от­бра­ковки делает ее очень эффективной [11].

Робастные методы оценивания математического ожидания и сред­него квадратичного отклонения можно использовать и при вычислении статистик критериев типа Граббса. Однако в этом случае обязательно следует учитывать, что метод оценивания отразится на распределениях статистик.

Работа выполнена при финансовой поддержке Минобразования РФ (проект № ТО2-3.3-3356)

Литература

1. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. – М.: Наука, 1983. – 416 с.

2. Frank E. Grubbs. Sample Criteria for Testing Outlying observations // Ann. Math. Statist, 1950. ­– Vol. 21. ­– No. 1. – P.27-58.

6. Смирнов Н.В. Оценка максимального члена в ряду наблюдений // Доклады АН СССР, 1941. – Т. 33. – № 5. – С. 346-349.

7. ГОСТ 11.002-73. Прикладная статистика. Правила оценки анормаль­ности результатов наблюдений. М.: Изд-во стан­дартов. 1982. – 26 с.

8. СТ СЭВ 545-77. Прикладная статистика. Правила оценки анор­маль­ности результатов наблюдений. М.: Изд-во стан­дартов. 1978. – 26 с.

9. Микешина Н.Г. Выявление и исключение аномальных значений // За­водская лаборатория. 1966. – Т. 22. – № 3. – С. 310-318.

10. Орлов А.И. Неустойчивость параметрических методов отбраковки рез­ко выделяющихся наблюдений // Заводская лаборатория. 1992. – Т. 58. – № 7. – С. 40-42.

11. Лемешко Б.Ю. Робастные методы оценивания и отбраковка аномаль­ных измерений // Заводская лаборатория. – 1997. – Т.63. – № 5. – С. 43-49.

12. Лемешко Б.Ю., Чимитова Е.В. Построение оптимальных L-оценок параметров сдвига и масштаба распределений по выборочным квантилям // Сибирский журнал индустриальной математики. 2001. – Т.4. – № 2. – С. 166-183.

13. Лемешко Б.Ю., Чимитова Е.В. Оптимальные L-оценки параметров сдвига и масштаба распределений по выборочным квантилям // За­водская лаборатория. Диагностика материалов. 2004. – Т.70. – № 1. – С. 54-66.

Источник