Для чего используют определение 7 класс
Что такое определение? 7-й класс
Класс: 7
Цель урока: научить давать развернутые определения.
1. Учебник под редакцией Т. А. Ладыженской «Школьная риторика», 7 класс, Москва, С – Баллас, 1998.
2. Раздаточный материал (языковые модели, позволяющие строить определения; различные типы определений, понятия риторического и научного определения);
3. Рисунок корабля, на парусах которого понятия того, что определяется (каюта, иллюминатор, круиз, герб, флаг, бриг, бригантина, баркентина, корабль), фотографии класса.
4. Мешочек с фишками (зеленые и желтые квадратики).
Ход урока
Кто не любит путешествовать? «Домосед», – скажете Вы. Но и он бороздит просторы вселенной, когда садится на диван, берет в руки пульт, включает телевизор и погружается в таинственную атмосферу голубого экрана. Книгочей? Ну, уж он точно великий путешественник. Многих из вас трудно оторвать от захватывающей книги. А что говорить об истинных путешественниках, отправляющихся в далекие и недалекие страны.
Это и будет темой нашего урока – путешествия, выяснить, ЧТО ТАКОЕ ОПРЕДЕЛЕНИЕ? Какова же цель нашего круиза? НАУЧИТЬСЯ ДАВАТЬ РАЗВЕРНУТЫЕ ОПРЕДЕЛЕНИЯ, СОСТОЯЩИЕ ИЗ НЕСКОЛЬКИХ ЧАСТЕЙ И ПОЗНАКОМИТЬСЯ С ЯЗЫКОВЫМИ МОДЕЛЯМИ, ПОЗВОЛЯЮЩИМИ СТРОИТЬ РАЗНЫЕ ТИПЫ ОПРЕДЕЛЕНИЙ. Чем сложнее цель, тем интереснее её решать.
Чтобы отправиться в путешествие и вернуться здоровыми и отдохнувшими, на берегу нам нужна разминка.
Готовясь к путешествию, туристы читают много литературы, знакомятся с маршрутом, запоминают специальные термины, которые пригодятся им в поездке.
Сколько почемучек всегда едет рядом с нами! И поэтому без четко сформулированных определений не обойтись. И хотя их много и они самые разнообразные, все они состоят из 2 частей:
Первая – это то, что определяется;
Вторая – это то, как, посредством чего оно определяется.
Работа с раздаточным материалом:
Прочитайте определения. Назовите в каждом из них обе части.
Формулировок определений очень много. Как же научиться их строить? Очень просто. Есть модели, зная которые ты легко наполнишь их содержанием. Рассмотрим, например, такое определение.
ПЛАНКТОНОМ называются одноклеточные водоросли и простейшие животные, не способные самостоятельно перемещаться в воде, а переносимые течением.
Разберем это определение. В нем определяется понятие «ПЛАНКТОН», вторая часть определения – раскрытие специфических признаков этого понятия. Обе части связаны глаголом «НАЗЫВАЕТСЯ». Значит, модель данного определения такова «ТО-ТО» НАЗЫВАЕТСЯ «ТЕМ-ТО». Эта конструкция помогает строить самые разнообразные (по содержанию) определения.
Работа с раздаточным материалом:
Рассмотрим языковые модели, позволяющие строить определения. Вклеим их в тетради.
Попробуйте, используя одну из моделей, дать определение «АКВАТОРИИ». В этом вам поможет этимология слова: «аква» – вода, «терра» – земля. (Акватория – водное пространство моря, океана, залива.)
А теперь поиграем. На корабле часто со взрослыми отдыхают и дети. Всем известно, что именно они, ребятишки, считаются первыми почемучками на планете. Путешественников, а это все вы, разделим на пап – мам и детей. В этом нам поможет наш зеленый мешок. Те, кто вы – берет для себя желтый квадратик, становятся почемучками (детьми), а те, кто выберет зеленый – родителями. Для того чтобы сформулировать свой вопрос, у наших малышей немного времени – время раздачи квадратиков. (Раздаются зеленые и желтые квадратики.)
Родители подошли к доске. Разберите своих детей, играющих на детской площадке. Присаживайтесь на свободные места. А теперь, малыши, ваши вопросы. И четкие, доступные, по одной из языковых моделей построенные определения, которые дадут ваши родители.
(Mах 13-14 вопросов из различных областей знаний)
Что ж потрудились родители на славу. Но в ответах мы часто слышали речевые ошибки, неточности, вместо важной информации второстепенную. Попробуем исправить некоторые ученические ответы. Откроем страницу 109 упражнение №123.
До сих пор мы говорили о научных (логических) определениях, в которых важно раскрыть сущность определяемого понятия. Но определения могут быть построены и по-другому.
Например: Море – это бездна проблем, тайн, непонятных вещей, нелепых вопросов и увлекательных загадок.
Такое определение называется риторическим.
Домашнее задание
Найти научные и риторические определения.
А раз мы заговорили о домашнем задании, то круиз подходит к концу. Я, думаю, что он не только развлекал, но и научил вас давать развернутые определения и умело использовать их в речи. Значит, цель достигнута.
Урок риторики в 7 классе Мы строим определения (программа «Школа 2100»)
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Урок риторики в 7 классе. Программа «Школа 2100»
Тема: «Мы строим определения»
Цель : на основе ранее полученных знаний (6 кл. «Что такое ученические ответы») познакомить учащихся с понятиями «определение».
закрепление знания о видах определений, моделях определений; устных жанрах учебно-научной речи: описательное определение, группировка, классификационное высказывание;
выработка у уч-ся умения определять особенности устных жанров учебно-научной речи, их структурно-смысловые особенности;
развитие умения слушать научную речь. Отработка сигналов слушающих. Определение особенностей устной речи: избыточность паузы, колебания, обдумывание, паузы трудностей выражения мысли и т.д.;
закрепление понятия «устные жанры учебно-научной речи».
II Проверка домашнего задания: уч-ся зачитывают выписанные в тетрадь определения из учебников 7 класса, относящиеся к разным группам, устно анализируют их ( 1) через родовое и видовое понятие; 2) определение предмета через ряд действий, отвечающих на вопрос о том, обладает ли предмет свойством, характерным именно для него; 3) определение предмета (понятия) через указание способа его образования, возникновения, построения, цели употребления).
III 1. Запись в тетради даты, темы урока. Постановка цели урока.
2. Тренировка в построении разных определений
Упр 118. Приводим языковую модель, с помощью которой можно сформулировать практически любое определение. Разговор Грамматика и Риторика поясняет, что для этого необходимо наполнить ее лишь конкретным материалом. Уч-ся предлагается построить 3 определения по модели «ТО-ТО НАЗЫВАЕТСЯ ТЕМ-ТО». Например:
Кругом называется часть плоскости, ограниченная окружностью
Предлоги, образованные от самостоятельных частей речи (существительных, наречий, деепричастий), называются производными.
Тканями (биол) называются группы клеток, сходных по строению, происхождению и выполняемым функциям.
Упр 119 Освоение школьниками других языковых моделей путем анализа определений, в которых основные слова, составляющие каркас моделей, выделены жирным шрифтом.
Вопросы для анализа:
Назовите в определении его главную часть.
Прочитайте вторую часть определения, в которой раскрываются (указываются) специфические признаки определяемого понятия.
Какими словами связаны обе части определения?
Заключительная часть этого этапа работы – анализ теоретического материала на плашке (стр. 104)
Языковые модели, помогающие строить определения:
то-то называется тем-то (т.п.)
то-то является тем-то (т.п.)
то-то изучает то-то (в.п.)
то-то относится к тому-то (в.п.)
Обратить внимание на падежи!
3. Самостоятельная работа учащихся
Упр. 120 Формулировка определений с использованием разнообразных языковых моделей.
Пассаты – устойчивые ветры, направленные к экватору и возникающие между областями высокого давления 30-х широт и экваториальной областью низкого давления.
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Фреской является вид живописи, полученной путем нанесения водяных красок на сырую штукатурку.
Материком называют крупный массив земной коры, большая часть которого выступает над уровнем Мирового океана, а периферия находится ниже его уровня.
Упр 121. Узнай по описанию. Уч-ся перестраивают определения, следуя рекомендации учителя избегать однотипных моделей.
Как можно сказать иначе?
Сформулируйте то же определение, используя другую модель.
Построй определение по другой модели.
Упр. 122. Задания выполняются в форме игры «Кто такой? Что такое?»
Класс разделяется на две группы, выбирают жюри. Высший оценочный балл за наиболее точные, правильные и быстрые ответы.
Акватория – водное пространство моря, океана или залива.
Активно плавающих животных называют нектон.
Один из видов украшения ювелирных изделий называется зернью, потому что в основу техники украшение положены мельчайшие золотые или серебряные шарики, похожие на зерна. Отсюда – «Зернь – вид украшения ювелирных изделий, при котором рисунок составляют мельчайшие золотые или серебряные шарики (зерна), напаянные на поверхность изделия».
Карты называют тематическими, т.к. они собраны по темам: одни рассказывают о климате, другие о почвах и т.д. Карты называются тематическими, потому что в них рассказывается о компонентах природы: в физических картах – о рельефе земной поверхности; в климатических – о климате; в почвенных – о почвах разных территорий.
«Закупами» называли свободных крестьян, обращенных за долги (за «купу») во временно зависимых.
Параллелограммом называют четырехугольник, у которого противоположные стороны попарно равны и параллельны.
Последнее задание – разыграть фрагмент урока по русскому языку.
Объявление результатов (жюри) и оценок (учитель)
Упр 124. Повторение типов определений: научное (логическое) и риторическое. На материале упражнения – анализ пар определений, доказательство их принадлежности к тому или иному типу.
IV Подведение итогов (рефлексия)
Что вызвало затруднения? Над чем надо еще поработать?
Что особенно понравилось?
Насколько мы достигли поставленной цели?
V Домашнее задание
Упр 123. Выявление и исправление речевых ошибок в формулировках определений.
Упр 125 Подготовка сообщения младшим школьникам. Попробуйте заинтересовать их, увлечь предметом своей речи. Решая эту задачу, вы постараетесь изложить научную информацию в более популярной, доступной, интересной форме. Замените данные в тексте логические определения риторическими
График линейной функции, его свойства и формулы
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
Понятие линейной функции
Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Для удобства результаты можно оформлять в виде таблицы:
Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».
| Функция | Коэффициент «k» | Коэффициент «b» |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b».
Еще не устали? Изучать математику веселее с опытным преподавателем на курсах по математике в Skysmart!
Свойства линейной функции
Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1 /3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.
В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).
В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.
Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).
Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.
При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.
Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.
Если k 0, то график функции y = kx + b выглядит так:
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
Точки пересечения графика функции y = kx + b с осями координат:
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Сила упругости
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
Сила — это физическая векторная величина, которую воздействует на данное тело со стороны других тел.
Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.
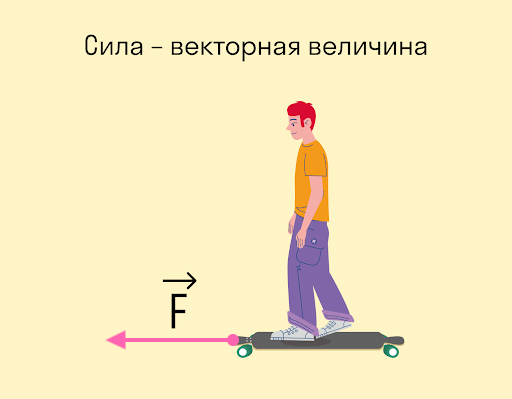
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Деформация
Деформация — это изменение формы и размеров тела (или части тела) под действием внешних сил
Происходит деформация из-за различных факторов: при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела.
Деформация является деформацией, пока сила, вызывающая эту деформацию, не приведет к разрушению.
На появление того или иного вида деформации большое влияние оказывает характер приложенных к телу напряжений. Одни процессы деформации связаны с преимущественно перпендикулярно (нормально) приложенной силой, а другие — преимущественно с силой, приложенной по касательной.
По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом:
Сила упругости: Закон Гука
Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не стремится вернуться в исходное состояние).
При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.
Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, пропорциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.
Какой буквой обозначается сила упругости?
Закон Гука
Fупр = kx
Fупр — сила упругости [Н]
k — коэффициент жесткости [Н/м]
х — изменение длины (деформация) [м]
Изменение длины может обозначаться по-разному в различных источниках. Варианты обозначений: x, ∆x, ∆l.
Это равноценные обозначения — можно использовать любое удобное.
Поскольку сила упругости направлена против направления силы, с которой это тело деформируется (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках. Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.
Задачка
На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при поднятии вверх рыбы весом 300 г?
Решение:
Сначала определим силу, которая возникает, когда мы что-то поднимаем. Это, конечно, сила тяжести. Не забываем массу представить в единицах СИ – килограммах.
Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :
Тогда из Закона Гука выразим модуль удлинения лески:
Выражаем модуль удлинения:
Подставим числа, жесткость лески при этом выражаем в Ньютонах:
x=3/(0,3 * 1000)=0,01 м = 1 см
Ответ: удлинение лески равно 1 см.
Параллельное и последовательное соединение пружин
В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.
Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.
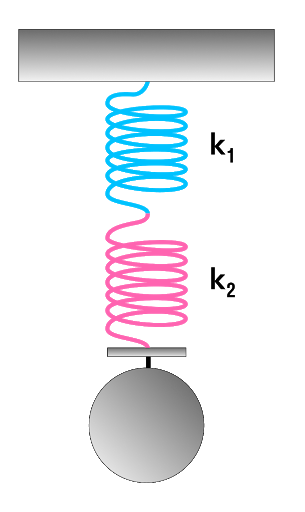
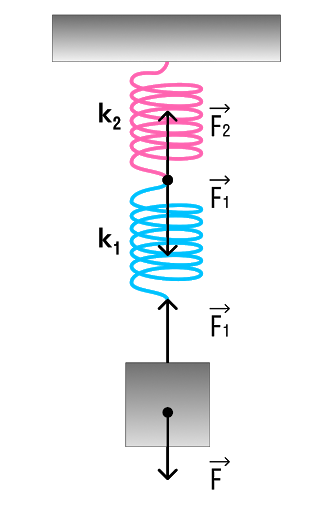
Последовательное соединение системы пружин
Последовательное соединение характерно наличием одной точки соединения пружин.
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
Коэффициент жесткости при последовательном соединении пружин
1/k = 1/k₁ + 1/k₂ + … + 1/k_i
k — общая жесткость системы [Н/м] k1, k2, …, — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]
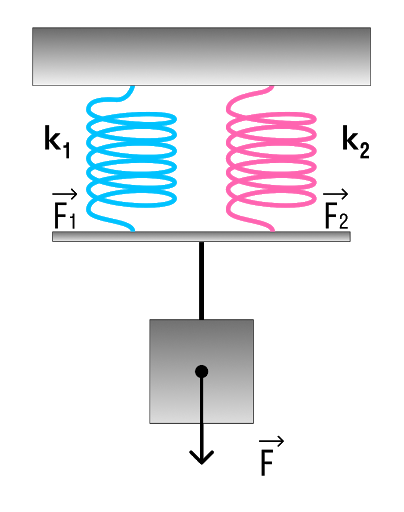
Параллельное соединение системы пружин
Последовательное соединение характерно наличием двух точек соединения пружин.
В случае когда пружины соединены параллельно величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
Коэффициент жесткости при параллельном соединении пружин
k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]
Задачка
Какова жесткость системы из двух пружин, жесткости которых k₁ = 100 Н/м, k₂ = 200 Н/м, соединенных: а) параллельно; б) последовательно?
Решение:
а) Рассмотрим параллельное соединение пружин.
При параллельном соединении пружин общая жесткость
k = k₁ + k₂ = 100 + 200 = 300 Н/м
б) Рассмотрим последовательное соединение пружин.
При последовательном соединении общая жесткость двух пружин
1/k = 1/100 + 1/200 = 0,01 + 0,005 = 0,015
k = 1000/15 = 200/3 ≃ 66,7 Н/м
График зависимости силы упругости от жесткости
Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.
Задачка 1
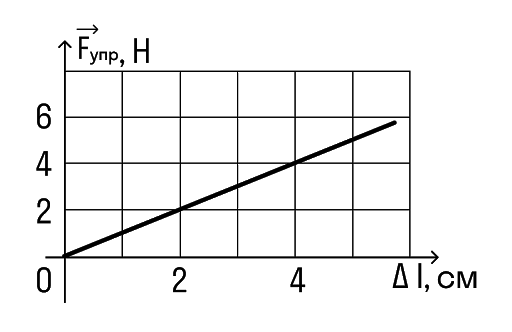
Определите по графику коэффициент жесткости тела.
Решение:
Из Закона Гука выразим коэффициент жесткости тела:
Снимем значения с графика. Важно выбрать одну точку на графике и записать для нее значения обеих величин.
Например, возьмем вот эту точку.
В ней удлинение равно 2 см, а сила упругости 2 Н.
Переведем сантиметры в метры: 2 см = 0,02 м И подставим в формулу: k = F/x = 2/0,02 = 100 Н/м
Ответ:жесткость пружины равна 100 Н/м
Онлайн-уроки физики в Skysmart не менее увлекательны, чем наши статьи!
Задачка 2
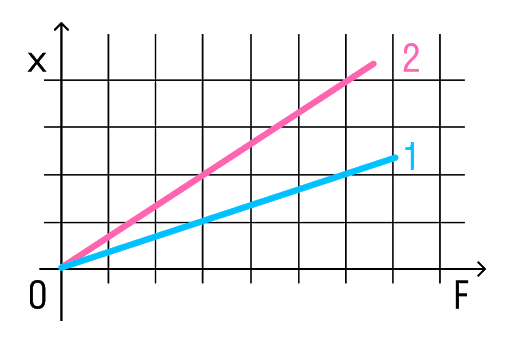
На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра. Сравнить жесткости проволок.
Решение:
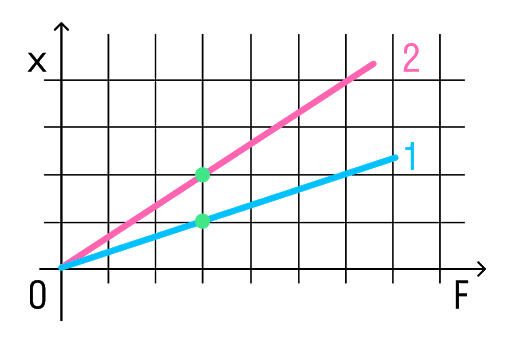
Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.
Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.
Значит жесткость стальной проволоки больше.
Ответ: жесткость стальной проволоки больше медной.