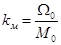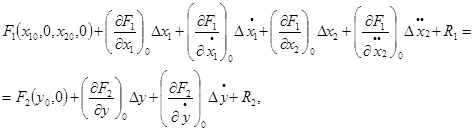Линеаризация характеристик датчиков

Линеаризация характеристик датчиков — нелинейное преобразование выходной величины датчика или величины (аналоговой или цифровой), ей пропорциональной, посредством которого достигается линейная зависимость между измеряемой и представляющей ее величинами.

Пользуясь линеаризацией, можно добиться линейности шкалы вторичного прибора, к которому подключен датчик с нелинейной характеристикой (например, термопара, термосопротивление, газоанализатор, расходомер и др.). Линеаризация характеристик датчиков дает возможность получить требуемую точность измерения вторичными приборами с цифровым выходом. Она необходима в ряде случаев при подключении датчиков к записывающим приборам или при выполнении над измеряемой величиной математических операций (например, интегрирования).

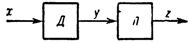
По отношению к характеристике датчика линеаризация выступает как обратное функциональное преобразование. Если характеристику датчика представить как y=F (а + b х), где х — измеряемая величина, а и b — постоянные, то характеристика линеаризатора, включаемого последовательно с датчиком (рис. 1), должна иметь вид: z=k F (у), где F — функция, обратная F.

В результате на выходе линеаризатора будет получено z = k F (F(a+bx)) = a’+b’x, т. е. линейная функция измеряемой величины.

Рис. 1. Обобщенная блок-схема линеаризации: Д— датчик, Л — линеаризатор.

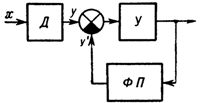
В дальнейшем путем масштабирования зависимость z приводится к виду z’ = mx, где m — соответствующий масштабный коэффициент. Если линеаризация производится компенсационным способом, т. е. на основе следящей системы типа рис. 2, то характеристика линеаризующего преобразователя функционального должна быть подобна характеристике датчика z = cF (a+bx), т. к. линеаризованное значение измеряемой величины снимается со входа функционального преобразователя-линеаризатора, а выход его сравнивается с выходной величиной датчика.

Особенностью линеаризаторов как функциональных преобразователей является сравнительно узкий класс воспроизводимых ими зависимостей, ограничивающийся монотонными функциями, что определяется видом характеристик датчиков.

Рис. 2. Блок-схема линеаризации на основе следящей системы: Д — датчик, У — усилитель (преобразователь), ФП — функциональный преобразователь.

Линеаризаторы можно классифицировать по следующим признакам:

2. По степени гибкости схемы: универсальные (т. е. перенастраиваемые) и специализированные.

3. По характеру структурной схемы: разомкнутого (рис. 1) и компенсационного (рис. 2) типов.

4. По форме входных и выходных величин: аналоговые, цифровые, смешанного характера (аналого-цифровые и цифро-аналоговые).

5. По типу применяемых в схеме элементов: механические, электромеханические, магнитные, электронные и др.

К числу линеаризаторов с пространственным заданием функции прежде всего относятся механизмы на кулачках, лекалах и нелинейных потенциометрах. Они используются в тех случаях, когда измеряемая величина на какой-либо ступени преобразования представлена в виде механического перемещения (кулачки — для линеаризации характеристик манометрических и трансформаторных датчиков, лекала — в самопишущих приборах, нелинейные потенциометры — в потеициометрических и мостовых схемах).

Нелинейность характеристик потенциометров достигается намоткой на профилированных каркасах и секционированием по методу кусочно-линейной аппроксимации путем шунтирования секций соответствующими сопротивлениями.

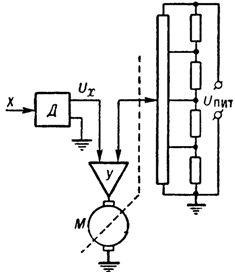
В линеаризаторе, основанном на электромеханической следящей системе потеициометрического типа с использованием нелинейного потенциометра (рис. 3), линеаризованная величина выступает в виде угла поворота или механического перемещения. Эти линеаризаторы просты, универсальны и широко распространены в системах централизованного контроля.

Рис. 3. Линеарнзатор электромеханической следящей системе потенциометрического типа: Д — датчик с выходом в виде пост, напряжения, У — усилитель, М — электродвигатель.

Нелинейности характеристик отдельных элементов (электронных, магнитных, тепловых и др.) используются в параметрических функциональных преобразователях. Однако между отрабатываемыми ими функциональными зависимостями и характеристиками датчиков обычно не удается добиться полного соответствия.

Алгоритмический способ задания функции применяется в цифровых функциональных преобразователях. Их достоинства — высокая точность и стабильность характеристик. В них используются математические свойства отдельных функциональных зависимостей или принцип кусочно-линейной аппроксимации. Например, парабола отрабатывается на основании и свойства квадратов целых чисел.

На методе кусочно-линейной аппроксимации основан, например, цифровой линеаризатор, работающий на принципе заполнения отрезков аппроксимации импульсами различных частот следования. Частоты заполнения изменяются скачками в граничных точках отрезков аппроксимации по программе, закладываемой в устройство в соответствии с видом нелинейности. Линеаризуемая величина преобразуется при этом в унитарный код.

Кусочно-линейная аппроксимация нелинейности может также осуществляться цифровым линейным интерполятором. При этом частоты заполнения интервалов интерполяции остаются постоянными лишь в среднем.

Преимущества цифровых линеаризаторов, основанных на методе кусочно-линейной аппроксимации: легкость перенастройки набранной нелинейности и быстрота переключений с одной нелинейности на другую, что особенно важно в быстродействующих системах централизованного контроля.

В сложных управляющих системах, содержащих универсальные вычислит, машины, линеаризация может выполняться непосредственно этими машинами, в которые функция закладывается в виде соответствующей подпрограммы.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Дифференциальные уравнения. Линеаризация.

Известно, что любое движение, процессы передачи, обмена, преобразования энергии и вещества математически можно описать в виде дифференциальных уравнений (ДУ). Любые процессы в АСР также принято описывать дифференциальными уравнениями, которые определяют сущность происходящих в системе процессов независимо от ее конструкции и т.д. Решив ДУ, можно найти характер изменения регулируемой переменной в переходных и установившихся режимах при различных воздействиях на систему.

Для упрощения задачи нахождения ДУ, описывающего работу АСР в целом, систему разбивают на ее отдельные элементы, переходные процессы в которых описываются достаточно простыми ДУ. Так как ДУ описывают работу системы независимо от физической сущности протекающих в ней процессов, то при разбивке системы нет необходимости учитывать их физическую целостность. Для каждого элемента структурной схемы необходимо составить ДУ, определяющее зависимость изменения выходной величины от входной.

Так как выходная величина предыдущего элемента является входной для последующего, то, определив ДУ отдельных элементов, можно найти ДУ системы.

Однако, такой метод применим только в частных случаях. Дело в том, что в большинстве случаев в реальных элементах системы связь между входной и выходной величинами является нелинейной и часто задается в графической форме. Поэтому, даже если ДУ системы и будет получено, оно будет нелинейным. А аналитическое решение нелинейных ДУ возможно далеко не всегда.

Для решения этой проблемы учитывают, что в процессе регулирования отклонения всех изменяющихся величин от их установившихся значений малы, и поэтому возможна замена нелинейных ДУ приближенными линейными ДУ, то есть возможна линеаризация дифференциальных уравнений.

Рассмотрим сущность процесса линеаризации на примере сушильного шкафа. Зависимость температуры объекта от подаваемого напряжения в большинстве случаев нелинейна и имеет вид, представленный на рисунке.

Графически линеаризацию некоторого уравнения от двух переменных F(х,у) = 0 в окрестности некоторой точки (х₀, у₀) можно представить как замену рассматриваемого участка кривой на касательную (см. рис. 1.14), уравнение которой определяется по формуле:

,

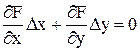
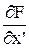
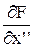
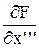
Линеаризация ДУ происходит аналогично, отличие состоит только в том, что необходимо искать частные производные по производным ( , , и т.д.).

Пример. Линеаризация нелинейного ДУ.

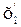
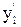
Данное ДУ является нелинейным из-за наличия произведений переменных х и у. Линеаризируем его в окрестности точки с координатами х₀ = 1, = 0, = 0. Для определения недостающего начального условия у₀ подставим данные значения в ДУ:

Введем в рассмотрение функцию

и определим все ее производные при заданных начальных условиях:

= (1,5у = 1,5*2 = 3,

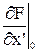
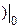
Теперь, используя полученные коэффициенты, можно записать окончательное линейное ДУ:

Источник

Суть и способы линеаризации нелинейных динамических систем

Линеаризация позволяет выявить большинство качественных и особенно количественных свойств нелинейной системы.

Методы линеаризации имеют ограниченный характер, то есть эквивалентность исходной нелинейной системы и ее линейного приближения сохраняется лишь для ограниченных пространственных или временных масштабов системы, или для определенных процессов, причем, если система переходит из одного режима работы в другой, то следует изменить и ее линеаризованную модель.

Линеаризация нелинейных динамических систем методом замены переменных

Линеаризация системы нелинейных уравнений в окрестности точки равновесия может быть достигнута путем замены переменных так, чтобы точка равновесия превратилась в начало координат.

Уравнения, полученные в результате указанного действия, будут линейными и называться линеаризацией исходной системы. Точки исходной системы, находящиеся в окрестности точки равновесия, будут соответствовать точкам в окрестности начала координат новой системы. Нас будет интересовать:

Рассмотрим нелинейную систему: (1) что имеет точки равновесия (p, q). Преобразование u=x-p v=y-q переводит точки равновесия p, q в начало координат. Дифференцирование дает: (2) После замены переменных, подставив их новые значения в каждое уравнение, выделим линейную часть: где F(u,v) и G(u,v) и состоят только из нелинейных выражений. Говорят, что линейная система есть линерализацией системы (1) при таких условиях: Эти последние условия обеспечивают то, что нелинейные выражения F(u,v) и G(u,v) на столько малы по сравнению с u и v при приближении к точке равновесия, что ими можно пренебречь.

Линеаризация на основе якобиана

Замену переменных можно использовать и при другой организации линеаризации. Производят замену: где Это может быть записано в виде: где называется якобиан.

Источник

Составление уравнений САР и их линеаризация

Объекты управления и управляющие устройства обычно являются весьма сложными динамическими системами, в которых протекают процессы, имеющие часто различную физическую природу, и на которые действуют различные физические воздействия. Понятно, что описать всю систему одним уравнением весьма сложно. Для упрощения обычно систему разбивают на отдельные элементы и дают математическое описание процессов в них и связей между ними. Уравнения элементов составляются на основе физических законов, определяющих протекание процессов в них.

а) для процессов связанных с образованием или преобразованием веществ (обычно, при химических реакциях), а также связанных с переносом веществ, применяют закон сохранения вещества, который приводит к уравнениям материального баланса;

б) для процессов, связанных с преобразованием различных видов энергии, применяют закон сохранения энергии который приводит к уравнениям энергетического баланса в частности, к уравнениям теплового баланса;

в) для процессов, связанных с механическим перемещением и взаимодействием тел, материалов, применяют законы Ньютона, в частности, уравнение Даламбера для вращающихся тел:

, (3-2)

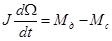
где Ω. — угловая скорость тела;

I — момент инерции относительно оси вращения;

М_д, М_с — соответственно движущий момент и момент сопротивления;

г) для электрических и электронных схем — законы Ома и Кирхгофа:

(3-3)

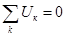
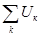
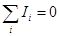
где —сумма напряжений по замкнутому контуру,

(3-4)

где 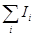, — сумма токов в узле.

Надо отметить, что различные физические процессы могут описываться, как увидим далее, аналогичными уравнениями. «Единство природы обнаруживается в «поразительной аналогичности» дифференциальных уравнений относящихся к разным областям явлений» (В. И. Ленин Соч., изд. 4, т. 14, стр. 276).

(3-5)

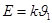
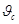
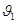
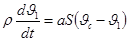
Однако измеряемая температура окружающей горячий спай среды не совпадает с температурой . При конвективном теплообмене между корпусом ТП и окружающей средой уравнение теплового баланса устанавливает, что скорость изменения температуры горячего спая ТП пропорциональна разности температур среды и горячего спая, поэтому

(3-6)

где ρ — теплоемкость корпуса ТП;

S — площадь поверхности корпуса ТП;

а — коэффициент теплоотдачи;

, (3-7)

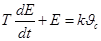
где .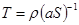

Пример 3-2. В качестве исполнительных устройств САР часто применяют двигатели (электрические, гидравлические, пневматические). Рассмотрим двигатель с

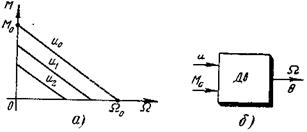
Рис. 3-1. Двигатель с линейными механическими характеристиками

линейными механическими характеристиками (рис. 3-1,а), когда движущий момент растет пропорционально управлению и и падает пропорционально скорости Ω

, (3-8)

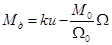
где М₀ — пусковой момент;

Ω₀ — скорость холостого хода. По Даламберу (см. (3-2))

,

, (3-9)

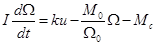
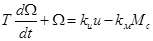
где , ,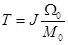

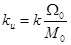
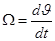
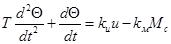
Таким образом, двигатель как элемент САР имеет два входных воздействия — управляющее и и возмущающее М_с (рис. 3-1,б) и одну выходную переменную — скорость Ω Однако в ряде случаев нас будет интересовать не скорость Ω, вала двигателя, а его угловое положение Θ (в следящих системах, в астатических системах с сервоприводом и др.). Поскольку , то уравнение двигателя относительно положения вала запишется с учетом (3-9) как

. (3-1)

Полученные уравнения могут оказаться нелинейными, хотя нелинейность при малых отклонениях от номинальных значений входных воздействий обычно бывает незначительной. В таких случаях уравнения линеаризуют методом малых отклонений. Физический смысл метода, обоснованного одним из основоположников теории автоматического управления русским ученым А. М. Ляпуновым (1857—1918 состоит в том, что обычно САР работает в номинально установившемся режиме, отклонения от которого под действием возмущений достаточно малы, поскольку САР проектируется таким образом, чтобы противодействовать возмущениям. Таким образом, обычно выполняется гипотеза о малости отклонений, когда нелинейностью, если она гладкая, можно пренебречь. Математически линеаризацию полученных уравнений осуществляют с помощью разложения в ряд Тейлора, в котором пренебрегают нелинейными членами. В самом деле, пусть некоторый элемент САР описывается нелинейным дифференциальным уравнением, например,

, (3-11)

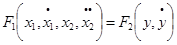
где F₁, F₂ — нелинейные функции от своих аргументов.

Допустим, что установившийся процесс в САР имеет место, когда х₁=х₁₀, х₂ = х₂₀, у=у₀. Тогда уравнение установившегося режима имеет вид

. (3-12)

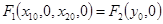
Рассмотрим (3-11) при малых отклонениях Δ от установившегося режима. Разлагая по Тейлору (3-11) в ряд в точке (х₁₀, х₂₀, у₀), получаем

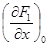
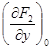
где , —частные производные, вычисленные в точке установившегося режима, т. е. некоторые числа;

R₁, R₂ — остаточные члены разложения, содержащие члены с приращениями высшего порядка (в них-то и заключена вся нелинейность).

Так как приращения считаются малыми, то остаточные члены R₁, R₂ содержат величины высшего порядка малости, которыми можно пренебречь. В этом случае, исключая из последнего уравнения выражение (3-12) для установившегося режима, получаем так называемые уравнения первого приближения (уравнения в «вариациях»), которые являются линейными для приращений,

, (3-13)

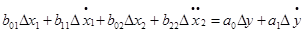
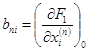
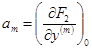
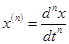
где , , , (n=0,1,2).

Обычно коэффициент а₀ делают равным 1, т. е. делят уравнение (3-13) на а₀. Кроме того, обозначение приращения Δ опускают при записи, понимая, что уравнение составлено для приращений.

Пример 3-3. Асинхронный двухфазный двигатель с полым или короткозамкнутым ротором, когда приведенное сопротивление ротора R_p (в величинах статорного сопротивления) соизмеримо с выходным сопротивлением R_в, источника управляющего напряжения (например, фазочувствительного усилителя ФУ, подключенного к управляющей обмотке двигателя, рис. 3-2,а), имеет механические характеристики, показанные на рис. 3-2,б, где Ω₀ — синхронная скорость (при R_p>>R_в характеристики показаны пунктиром). Как видим, механические характеристики отличаются

Рис. 3-2 Асинхронный двухфазный двигатель

от линейных, рассмотренных в примере 3-2. Разлагая гладкую нелинейную функцию М(и,Ω) в ряд по приращениям и и Ω и пренебрегая нелинейными членами, получаем линейное уравнение, аналогичное (3-8),

, (3-14)

, .

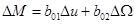
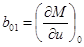
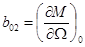
Интересно, что в некоторых точках механической характеристики коэффициент b₀₂ имеет разные знаки. Например, при малых отклонениях от скорости Ω₁ величина b₀₂ 0 (далее будет показано, что один режим является устойчивым, а другой неустойчивым).

Источник