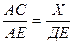Для чего необходимо определять среднюю точку попадания
Определение средней точки попадания. Закон рассеивания.
Причины рассеивания. Явление рассеивания
 Определение средней точки попадания (СТП)
Определение средней точки попадания (СТП)
Закон рассеивания
Причины рассеивания
Явление рассеивания
Определение средней точки попадания
По четырем пробоинам (точкам встречи) среднюю точку попадания можно определить еще так: рядом лежащие пробоины (точки встречи) соединить попарно, середины обоих прямых снова соединить и полученную линию разделить пополам; точка деления и будет средней точкой попадания.
При наличии пяти пробоин (точки встречи) средняя точка попадания для них определяется подобным же образом.
При большом числе пробоин (точек встречи) на основании симметричности рассеивания средняя точка попадания определяется способом проведения осей рассеивания.
Для этого нужно:
— отсчитать нижнюю (ближнюю) половину пробоин (точек встречи) и отделить ее осью рассеивания по высоте (дальности);
— отсчитать таким же порядком правую или левую половину пробоин (точек встречи) и отделить ее осью рассеивания по боковому направлению;
— пересечение осей рассеивания является средней точкой попадания.
Среднюю точку попадания (СТП) можно также определить способом вычисления (расчета).
Для этого необходимо:
— провести через левую (правую) пробоину (точку встречи) вертикальную линию, измерить кратчайшее расстояние от каждой пробоины (точки встречи) до этой линии, сложить все расстояния от вертикальной линии и разделить сумму на число пробоин (точек встречи);
— провести через нижнюю (верхнюю) пробоину (точку встречи) горизонтальную линию, измерить кратчайшее расстояние от каждой пробоины (точки встречи) до этой линии, сложить все расстояния от горизонтальной линия и разделить сумму на число пробоин (точек встречи).
Полученные числа определяют удаление СТП от указанных линий.
Закон рассеивания
При большом числе выстрелов (более 20) в расположении точек встречи на площади рассеивания наблюдается определенная закономерность. Рассеивание пуль подчиняется нормальному закону случайных ошибок, который отношении к рассеиванию пуль называется законом рассеивания.
Этот закон характеризуется следующими тремя положениями:
1. Точки встречи (пробоины) на площади рассеивания располагаются неравномерно — гуще к центру рассеивания и реже к краям площади рассеивания.
2. На площади рассеивания можно определить точку, являющуюся центром рассеивания (средней точкой попадания), относительно которой распределение точек встречи (пробоин) симметрично: число точек встречи по обе стороны от осей рассеивания, заключающихся в равных по абсолютной величине пределах (полосах), одинаково, и каждому отклонению от оси рассеивания в одну сторону отвечает такое же по величине отклонение в противоположную сторону.
3. Точки встречи (пробоины) в каждом частном случае занимают не беспредельную, а ограниченную площадь.
Таким образом, закон рассеивания в общем виде можно сформулировать так: при достаточно большом числе выстрелов, произведенных в практически одинаковых условиях, рассеивание пуль неравномерно, симметрично и небеспредельно.
Причины рассеивания
Причины, вызывающие рассеивание пуль, могут быть сведены в три группы:
— вызывающие разнообразие начальных скоростей;
— вызывающие разнообразие углов бросания и направления стрельбы;
— вызывающие разнообразие условий полета пули.
Причинами, вызывающими разнообразие начальных скоростей, являются:
— разнообразие в весе пороховых зарядов и пуль, в форме и размерах пуль и гильз, в качестве пороха, в плотности заряжания и т.д., как результат неточностей (допусков) при их изготовлении;
— разнообразие температур зарядов, зависящее от температуры воздуха и неодинакового времени нахождения патрона в нагретом при стрельбе стволе;
— разнообразие в степени нагрева и в качественном состоянии ствола.
Эти причины приводят к рассеиванию пуль по боковому направлению и дальности (высоте), оказывают наибольшее влияние на величину площади рассеивания и в основном зависят от выучки стреляющего.
Явление рассеивания
Совокупность траекторий пуль, полученных вследствие их естественного рассеивания, называется снопом траекторий. Траектория, проходящая в середине снопа траекторий, называется средней траекторией. Табличные и расчетные данные относятся к средней траектории.
Точка пересечения средней траектории с поверхностью цели (преградой) называется средней точкой попадания (или центром рассеивания).
Взаимно перпендикулярные линии, проведенные через среднюю точку попадания (СТП) так, чтобы одна из них совпадала с направлением стрельбы, называются осями рассеивания.
Кратчайшие расстояния от точек встречи (пробоин) до осей рассеивания называются отклонениями.
Способы определения положения средней точки попадания
Для этого необходимо:
— соединить прямой две пробоины (точки встречи) и расстояние между ними разделить пополам;
— полученную точку соединить с третьей пробоиной (точкой встречи) и расстояние между ними разделить на три равные части; так как к центру рассеивания пробоины (точки встречи) располагаются гуще, то за среднюю точку попадания трех пробоин
(точек встречи) принимается деление, ближайшее к двум первым пробоинам (точкам встречи);
По четырем пробоинам (точкам встречи) среднюю точку попадания можно определить еще так: рядом лежащие пробоины (точки встречи) соединить попарно, середины обеих прямых снова соединить и полученную линию разделить пополам; точка деления и будет средней точкой попадания.
При наличии пяти пробоин (точек встречи) средняя точка попадания для них определяется подобным же образом.
При большом числе пробоин (точек встречи) на основании симметричности рассеивания средняя точка попадания определяется способом проведения осей рассеивания.
Для этого нужно:
— отсчитать нижнюю (ближнюю) половину пробоин (точек встречи) и отделить ее осью рассеивания по высоте (дальности);
— отсчитать таким же порядком правую или левую половину пробоин (точек встречи) и отделить ее осью рассеивания по боковому направлению;
— пересечение осей рассеивания является средней точкой попадания.
Среднюю точку попадания можно также определить способом вычисления (расчета). Для этого необходимо:
Пробоин
Расстояние в см от пробоин до
СРЕДНЯЯ ТОЧКА ПОПАДАНИЯ, ЕЁ ОПРЕДЕЛЕНИЕ
Точность определения положения СТП зависит от количества выстрелов. Чем больше будет произведено выстрелов, тем точнее можно определить положение СТП.
Опытным путем и расчетами установлено, что для достаточной точности в определении положения СТП при стрельбе одиночными выстрелами требуется 4 пробоины, увеличение числа выстрелов незначительно повышает точность определения СТП, но в то же время приводит к увеличенному расходу боеприпасов.
Такое количество патронов при стрельбе очередями более полно выявляет рассеивание.
Для определения СТП при стрельбе из различных пулеметов установлено по 8 выстрелов и 10 выстрелов для станковых и крупнокалиберных пулеметов.
Средняя точка попадания (СТП) может быть определена несколькими способами. По трем-четырем пробоинам СТП определяется следующим способом.
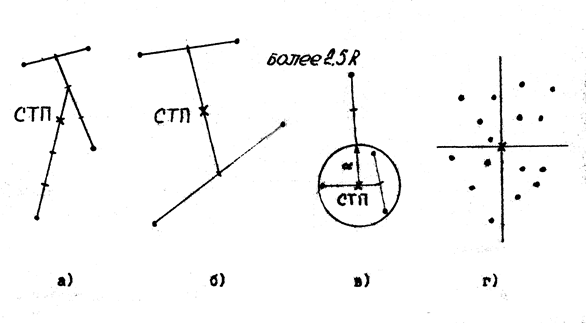
Ближайшие друг к другу пробоины (рис. 15 а) соединяют прямой линией и делят её пополам. Полученную точку соединяют с третьей пробоиной. А расстояние между ними делят на три равные части. Точку деления, ближайшую к двум первым пробоинам, соединяют с четвертой пробоиной и расстояние делят на четыре равные части. Точка деления, ближайшая к трем первым пробоинам, и будет СТП.
Можно пробоины соединить попарно (рис. 15 б), середины полученных прямых снова соединить, точка деления полученной прямой пополам и будет СТП.
Если одна из пробоин явно оторвалась от остальных, то ее следует отбросить как случайную и определить СТП по трем пробоинам.
Явно оторвавшейся пробоиной является такая, расстояние до которой от СТП остальных пробоин более 2,5 радиусов наименьшего круга, вмещающего эти остальные пробоины (рис. 15 в).
Рис. 15 Порядок определения средней точки попадания.
При большом числе (6-10) пробоин СТП определяется несколько иначе. Отбросив явно оторвавшиеся пробоины, остальные последовательно разделяют пополам вертикально и горизонтально проведенными линиями. Линии проводятся на равном удалении от двух ближайших пробоин, лежащих в плоскости деления. Точка пересечения линий деления принимается за СТП (рис.15 г).
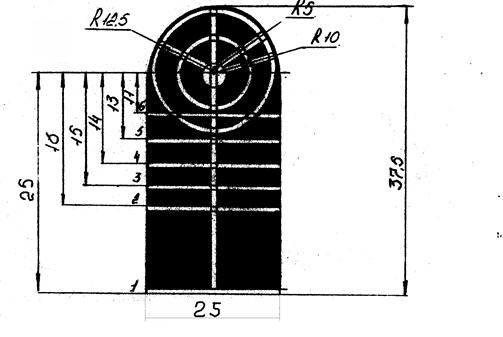
Точку прицеливания на проверочной мишени выбирают на пересечении белой вертикальной линии с нижним обрезом мишени, обозначенным цифрой (рис.16):
Рис. 16 Проверочная мишень (размеры даны в см).
2 – для снайперской винтовки;
3 – для пулемета Калашникова, ротного пулемета и ручных пулеметов под винтовочный патрон;
4 – для станковых пулеметов при стрельбе патронами с пулей образца 1930 г.;
5 – для станковых пулеметов при стрельбе патронами образца 1980 г. и 5,45-м автомата Калашникова;
6 – для пистолетов и револьверов, РПК-74;
7 – для 12,7-мм ручного пулемета Калашникова.
При отсутствии мишени размеры последней можно определить расчетным путем.
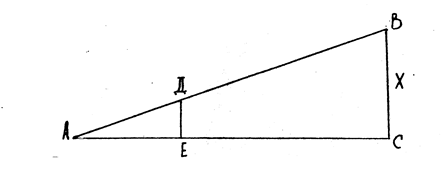
Пример: определить ширину мишени Х для приведения к нормальному бою АКМ, если дальность стрельбы АС равна 100 м, среднее расстояние от глаза стреляющего до мушки АЕ 0,8 м, диаметр (толщина) мушки ДЕ – 0,002м (рис. 17).
Решение: Из подобия треугольников АВС и АДЕ имеем:
откуда 
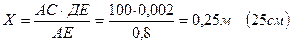
Рис.17 Определение ширины мишени.
Например, для автоматов, винтовок, карабинов и пулеметов берется дальность 100м, для пистолета АПС – 50м, для пистолетов и револьверов – 25м.
Эти дальности дают возможность избежать влияния метеорологических условий на полет пули и иметь хорошую точность прицеливания.
Глава 3.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Определение средней точки попадания. Закон рассеивания. Причины рассеивания. Явление рассеивания
Определение средней точки попадания (СТП)
Закон рассеивания
Причины рассеивания
Явление рассеивания
Определение средней точки попадания
По четырем пробоинам (точкам встречи) среднюю точку попадания можно определить еще так: рядом лежащие пробоины (точки встречи) соединить попарно, середины обоих прямых снова соединить и полученную линию разделить пополам; точка деления и будет средней точкой попадания.
При наличии пяти пробоин (точки встречи) средняя точка попадания для них определяется подобным же образом.
При большом числе пробоин (точек встречи) на основании симметричности рассеивания средняя точка попадания определяется способом проведения осей рассеивания.
Для этого нужно:
— отсчитать нижнюю (ближнюю) половину пробоин (точек встречи) и отделить ее осью рассеивания по высоте (дальности);
— отсчитать таким же порядком правую или левую половину пробоин (точек встречи) и отделить ее осью рассеивания по боковому направлению;
— пересечение осей рассеивания является средней точкой попадания.
Среднюю точку попадания (СТП) можно также определить способом вычисления (расчета).
Для этого необходимо:
— провести через левую (правую) пробоину (точку встречи) вертикальную линию, измерить кратчайшее расстояние от каждой пробоины (точки встречи) до этой линии, сложить все расстояния от вертикальной линии и разделить сумму на число пробоин (точек встречи);
— провести через нижнюю (верхнюю) пробоину (точку встречи) горизонтальную линию, измерить кратчайшее расстояние от каждой пробоины (точки встречи) до этой линии, сложить все расстояния от горизонтальной линия и разделить сумму на число пробоин (точек встречи).
Полученные числа определяют удаление СТП от указанных линий.
Закон рассеивания
При большом числе выстрелов (более 20) в расположении точек встречи на площади рассеивания наблюдается определенная закономерность. Рассеивание пуль подчиняется нормальному закону случайных ошибок, который отношении к рассеиванию пуль называется законом рассеивания.
Этот закон характеризуется следующими тремя положениями:
1. Точки встречи (пробоины) на площади рассеивания располагаются неравномерно — гуще к центру рассеивания и реже к краям площади рассеивания.
2. На площади рассеивания можно определить точку, являющуюся центром рассеивания (средней точкой попадания), относительно которой распределение точек встречи (пробоин) симметрично: число точек встречи по обе стороны от осей рассеивания, заключающихся в равных по абсолютной величине пределах (полосах), одинаково, и каждому отклонению от оси рассеивания в одну сторону отвечает такое же по величине отклонение в противоположную сторону.
3. Точки встречи (пробоины) в каждом частном случае занимают не беспредельную, а ограниченную площадь.
Таким образом, закон рассеивания в общем виде можно сформулировать так: при достаточно большом числе выстрелов, произведенных в практически одинаковых условиях, рассеивание пуль неравномерно, симметрично и небеспредельно.
Причины рассеивания
Причины, вызывающие рассеивание пуль, могут быть сведены в три группы:
— вызывающие разнообразие начальных скоростей;
— вызывающие разнообразие углов бросания и направления стрельбы;
— вызывающие разнообразие условий полета пули.
Причинами, вызывающими разнообразие начальных скоростей, являются:
— разнообразие в весе пороховых зарядов и пуль, в форме и размерах пуль и гильз, в качестве пороха, в плотности заряжания и т.д., как результат неточностей (допусков) при их изготовлении;
— разнообразие температур зарядов, зависящее от температуры воздуха и неодинакового времени нахождения патрона в нагретом при стрельбе стволе;
— разнообразие в степени нагрева и в качественном состоянии ствола.
Эти причины приводят к рассеиванию пуль по боковому направлению и дальности (высоте), оказывают наибольшее влияние на величину площади рассеивания и в основном зависят от выучки стреляющего.
Явление рассеивания
Совокупность траекторий пуль, полученных вследствие их естественного рассеивания, называется снопом траекторий. Траектория, проходящая в середине снопа траекторий, называется средней траекторией. Табличные и расчетные данные относятся к средней траектории.
Точка пересечения средней траектории с поверхностью цели (преградой) называется средней точкой попадания (или центром рассеивания).
Взаимно перпендикулярные линии, проведенные через среднюю точку попадания (СТП) так, чтобы одна из них совпадала с направлением стрельбы, называются осями рассеивания.
Кратчайшие расстояния от точек встречи (пробоин) до осей рассеивания называются отклонениями.
Определение средней точки попадания. Закон рассеивания. Причины рассеивания. Явление рассеивания
Темы дня
Определение средней точки попадания
По четырем пробоинам (точкам встречи) среднюю точку попадания можно определить еще так: рядом лежащие пробоины (точки встречи) соединить попарно, середины обоих прямых снова соединить и полученную линию разделить пополам; точка деления и будет средней точкой попадания.
При наличии пяти пробоин (точки встречи) средняя точка попадания для них определяется подобным же образом.
При большом числе пробоин (точек встречи) на основании симметричности рассеивания средняя точка попадания определяется способом проведения осей рассеивания.
Для этого нужно:
— отсчитать нижнюю (ближнюю) половину пробоин (точек встречи) и отделить ее осью рассеивания по высоте (дальности);
— отсчитать таким же порядком правую или левую половину пробоин (точек встречи) и отделить ее осью рассеивания по боковому направлению;
— пересечение осей рассеивания является средней точкой попадания.
Среднюю точку попадания (СТП) можно также определить способом вычисления (расчета).
Для этого необходимо:
— провести через левую (правую) пробоину (точку встречи) вертикальную линию, измерить кратчайшее расстояние от каждой пробоины (точки встречи) до этой линии, сложить все расстояния от вертикальной линии и разделить сумму на число пробоин (точек встречи);
— провести через нижнюю (верхнюю) пробоину (точку встречи) горизонтальную линию, измерить кратчайшее расстояние от каждой пробоины (точки встречи) до этой линии, сложить все расстояния от горизонтальной линия и разделить сумму на число пробоин (точек встречи).
Полученные числа определяют удаление СТП от указанных линий.
При большом числе выстрелов (более 20) в расположении точек встречи на площади рассеивания наблюдается определенная закономерность. Рассеивание пуль подчиняется нормальному закону случайных ошибок, который отношении к рассеиванию пуль называется законом рассеивания.
Этот закон характеризуется следующими тремя положениями:
1. Точки встречи (пробоины) на площади рассеивания располагаются неравномерно — гуще к центру рассеивания и реже к краям площади рассеивания.
2. На площади рассеивания можно определить точку, являющуюся центром рассеивания (средней точкой попадания), относительно которой распределение точек встречи (пробоин) симметрично: число точек встречи по обе стороны от осей рассеивания, заключающихся в равных по абсолютной величине пределах (полосах), одинаково, и каждому отклонению от оси рассеивания в одну сторону отвечает такое же по величине отклонение в противоположную сторону.
3. Точки встречи (пробоины) в каждом частном случае занимают не беспредельную, а ограниченную площадь.
Таким образом, закон рассеивания в общем виде можно сформулировать так: при достаточно большом числе выстрелов, произведенных в практически одинаковых условиях, рассеивание пуль неравномерно, симметрично и небеспредельно.
Причины, вызывающие рассеивание пуль, могут быть сведены в три группы:
— вызывающие разнообразие начальных скоростей;
— вызывающие разнообразие углов бросания и направления стрельбы;
— вызывающие разнообразие условий полета пули.
Причинами, вызывающими разнообразие начальных скоростей, являются:
— разнообразие в весе пороховых зарядов и пуль, в форме и размерах пуль и гильз, в качестве пороха, в плотности заряжания и т. д., как результат неточностей (допусков) при их изготовлении;
— разнообразие температур зарядов, зависящее от температуры воздуха и неодинакового времени нахождения патрона в нагретом при стрельбе стволе;
— разнообразие в степени нагрева и в качественном состоянии ствола.
Эти причины приводят к рассеиванию пуль по боковому направлению и дальности (высоте), оказывают наибольшее влияние на величину площади рассеивания и в основном зависят от выучки стреляющего.
Совокупность траекторий пуль, полученных вследствие их естественного рассеивания, называется снопом траекторий. Траектория, проходящая в середине снопа траекторий, называется средней траекторией. Табличные и расчетные данные относятся к средней траектории.
Точка пересечения средней траектории с поверхностью цели (преградой) называется средней точкой попадания (или центром рассеивания).
Площадь, на которой располагаются точки встречи (пробоины) пуль, полученные при пересечении снопа траекторий с какой-либо плоскостью, называется площадью рассеивания.
Взаимно перпендикулярные линии, проведенные через среднюю точку попадания (СТП) так, чтобы одна из них совпадала с направлением стрельбы, называются осями рассеивания.
Кратчайшие расстояния от точек встречи (пробоин) до осей рассеивания называются отклонениями.
Tag: Оружие_Статьи_Боевое_оружие
Обсуди статью на форуме
 Определение средней точки попадания (СТП)
Определение средней точки попадания (СТП)