Для чего необходимо составлять функциональные зависимости
Для чего необходимо составлять функциональные зависимости
Можно сказать, что функциональные зависимости представляют собой связи типа «один ко многим», существующие внутри отношения.
Некоторые функциональные зависимости могут быть нежелательны.
Определение первой нормальной формы:
отношение находится в 1NF если значения всех его атрибутов атомарны.
Рассмотрим пример, заимствованный из уже упоминавшейся статьи Е.Ф.Кодда:
В базе данных отдела кадров предприятия необходимо хранить сведения о служащих, которые можно попытаться представить в отношении СЛУЖАЩИЙ(НОМЕР_СЛУЖАЩЕГО, ИМЯ, ДАТА_РОЖДЕНИЯ, ИСТОРИЯ_РАБОТЫ, ДЕТИ).
Их связь представлена на рис. 4.3.
Рис.4.3. Исходное отношение.
Для приведения исходного отношения СЛУЖАЩИЙ к первой нормальной форме необходимо декомпозировать его на четыре отношения, так как это показано на следующем рисунке:
Рис.4.4. Нормализованное множество отношений.
Здесь первичный ключ каждого отношения выделен синей рамкой, названия внешних ключей набраны шрифтом синего цвета. Напомним, что именно внешние ключи служат для представления функциональных зависимостей, существующих в исходном отношении. Эти функциональные зависимости обозначены линиями со стрелками.
неключевой атрибут функционально полно зависит от составного ключа если он функционально зависит от всего ключа в целом, но не находится в функциональной зависимости от какого-либо из входящих в него атрибутов.
Определение второй нормальной формы:
Отношение находится во 2НФ, если оно находится в 1НФ и каждый неключевой атрибут функционально полно зависит от ключа.
Отношение находится в 3НФ, если оно находится во 2НФ и каждый неключевой атрибут нетранзитивно зависит от первичного ключа.
Эта нормальная форма вводит дополнительное ограничение по сравнению с 3НФ.
Определение нормальной формы Бойса-Кодда:
Отношение находится в BCNF, если оно находится во 3НФ и в ней отсутствуют зависимости атрибутов первичного ключа от неключевых атрибутов.
Ситуация, когда отношение будет находится в 3NF, но не в BCNF, возникает при условии, что отношение имеет два (или более) возможных ключа, которые являются составными и имеют общий атрибут. Заметим, что на практике такая ситуация встречается достаточно редко, для всех прочих отношений 3NF и BCNF эквивалентны.
4.2.6. Многозначные зависимости и четвертая нормальная форма (4NF).
Многозначная зависимость является обобщением функциональной зависимости и рассматривает соответствия между множествами значений атрибутов.
Такие зависимости и называются многозначными и обозначаются как Нетрудно показать, что многозначные зависимости всегда образуют связанные пары, поэтому их часто обозначают Очевидно, что каждая функциональная зависимость является многозначной, но не каждая многозначная зависимость является функциональной.
Определение четвертой нормальной формы:
Отношение находится в 4NF если оно находится в BCNF и в нем отстутсвуют многозначные зависимости, не являющиеся функциональными зависимостями.
4.2.7. Зависимости по соединению и пятая нормальная форма (5NF).
Детально этот вопрос здесь мы не обсуждаем (полное изложение см. в книге К.Дейта), заметим лишь, что зависимость по соединению является обощением многозначной зависимости. Отношения, в которых имеются зависимости по соединению, не являющиеся одновременно ни многозначными, ни функциональными, также характеризуются аномалиями обновления. Поэтому, вводится понятие пятой нормальной формы.
Определение пятой нормальной формы:
Отношение находится в 5НФ тогда и только тогда, когда любая зависимость по соединению в нем определяется только его возможными ключами.
BestProg
Нормализация. Функциональные зависимости атрибутов. Примеры. Построение схем функциональных зависимостей
Перед изучением данной темы рекомендуется ознакомиться с темой:
Содержание
Поиск на других ресурсах:
1. Понятие функциональной зависимости. Определение. Примеры
После того, как таблица приведена к первой нормальной форме 1НФ, нужно определить функциональную зависимость между атрибутами (полями, столбцами) таблицы. Это необходимо для обеспечения максимально-возможной рациональности в построении таблиц базы данных.
A → B
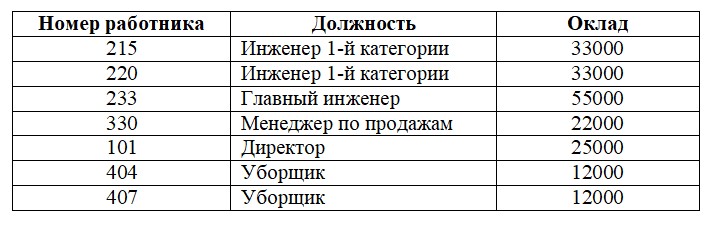
Пример 1. Пусть дано отношение, которое определяет должностные оклады работников некоторого предприятия.
Должность → Оклад
здесь Должность – детерминант, Оклад – зависимая часть.
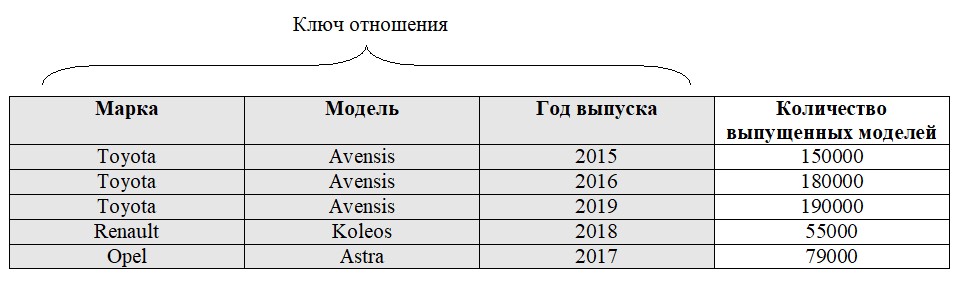
Пример 2. Демонстрируется зависимость атрибута от составного (композитного) ключа. На рисунке 1 изображена таблица выпуска различных моделей автомобилей в разные годы.
Рисунок 1. Функциональная зависимость атрибута « Количество выпущенных моделей » от ключа
2. Степени функциональной зависимости. Классификация
Различают следующие степени функциональной зависимости между атрибутами:
3. Частичная зависимость. Примеры
Пример 1. Пусть дана следующая таблица.
Поскольку атрибут Оклад зависит только от части ключа (атрибута Должность ) а не от всего ключа ( Номер работника — Должность ), то эта функциональная зависимость является частичной.
Рисунок 2 схематически отображает частичную зависимость.
Рисунок 2. Частичная зависимость атрибута Оклад от ключа отношения
Пример 2. Пусть дана таблица учета проведенных занятий в учебном заведении.
Рисунок 3. Частичная зависимость атрибута Дисциплина от ключа отношения
4. Полная функциональная зависимость. Примеры
Пример 1. Пусть дана база данных учета учебного процесса, таблица которой содержит атрибуты
Фрагмент таблицы базы данных следующий
Между этими атрибутами существует полная зависимость. Это означает, что за учебным годом можно определить курс, на котором учится студент. И, наоборот, по курсу обучения можно определить учебный год (при условии, что студент успешно сдал все сессии и не имеет задолженности по дисциплине «Организация баз данных и знаний» 🙂.
На схеме зависимостей такая связь обозначается следующим образом
Рисунок 4. Полная зависимость между атрибутами Год и Курс
Пример 2. Связь между идентификационным номером и именем гражданина. По имени гражданина можно определить идентификационный номер. И, наоборот, по идентификационному номеру можно определить имя гражданина.
5. Примеры транзитивной зависимости
Пример 1. Задана база данных, содержащая информацию о ходе учебного процесса в учебном заведении. В отношении (таблице) используются атрибуты (поля), имеющие транзитивные зависимости.
Между атрибутами Преподаватель и Группа существует транзитивная зависимость (рисунок 5).
Рисунок 5. Транзитивная зависимость между атрибутами Преподаватель и Группа
Поскольку, за каждой дисциплиной закреплен конкретный преподаватель, то между атрибутами Преподаватель и Группа существует транзитивная зависимость (Преподаватель преподает дисциплину в группе).
Пример 2. Пусть задана таблица начислений стипендии для студентов некоторой группы. Студенты могут учиться на госзаказе (бюджет) или по контракту.
От студента зависит вид договора на обучение: бюджет или контракт. Поэтому возникает функциональная зависимость между атрибутами Студент и Вид договора (рисунок 6).
Рисунок 6. Функциональная зависимость между атрибутами Студент и Вид договора
Вид договора влияет на размер стипендии. Если студент учится по контракту, то стипендия не начисляется. По размеру стипендии нельзя определить вид договора, поскольку студент может учиться на бюджете и не получать стипендию в связи с плохой успеваемостью. Поэтому, между атрибутами Вид договора и Стипендия существует следующая функциональная зависимость (рисунок 7).
Рисунок 7. Функциональная зависимость между атрибутами Вид договора и Стипендия
Значит между атрибутами Студент и Стипендия существует транзитивная зависимость (рисунок 8).
Рисунок 8. Транзитивная зависимость между атрибутами Студент и Стипендия
6. Примеры многозначной зависимости
Пример 1. В учебном заведении преподаватель может преподавать не одну а несколько родственных дисциплин.
Пример 2. Задана таблица стоимости новых автомобилей.
Между атрибутами Марка и Модель существует многозначная зависимость. Это объясняется тем, что для одной марки (Renault) может существовать несколько значений моделей (Logan, Megane, Koleos).
7. Задача. Построить схему функциональных зависимостей между атрибутами отношения
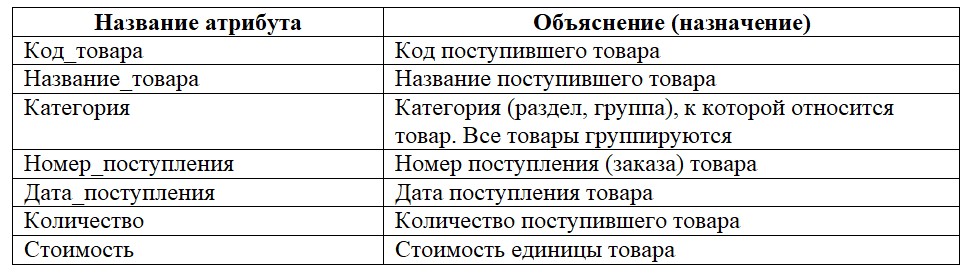
Условие задачи. Задана таблица базы данных «Учет товаров в автомагазине», которая приведена к первой нормальной форме 1НФ. Таблица определяет товары, поступающие на склад и имеет следующую структуру
Нужно построить схему зависимостей между атрибутами.
Решение. Схема зависимостей между атрибутами таблицы учета поступивших товаров на складе изображена на рисунке 9.
Рисунок 9. Схема зависимостей между атрибутами
8. Задача. Построить схему функциональных зависимостей между атрибутами отношения
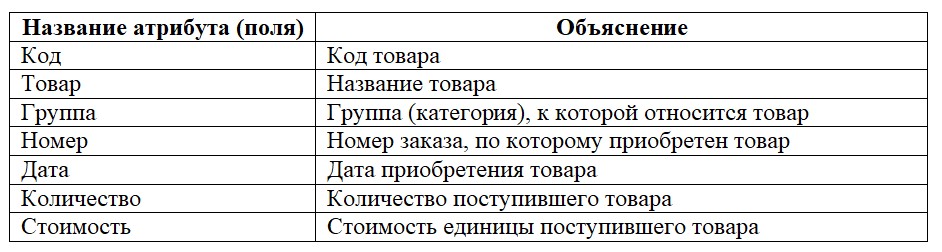
Задано таблицу базы данных магазина, которая отображает учет автозапчастей (товаров). Структура таблицы следующая
Рисунок 10. Схема функциональных зависимостей. Учет автозапчастей в магазине
9. Понятие независимых атрибутов. Примеры
Между отдельными атрибутами базы данных могут отсутствовать какие-либо функциональные зависимости. Такие атрибуты называются независимыми друг от друга.
Пример. Задана таблица с данными о преподавателе.
В вышеприведенной таблице нет функциональной зависимости между следующими атрибутами:
Полная функциональная зависимость в нормализации базы данных
Это не так сложно, как может показаться. Давайте посмотрим на это более подробно.
Краткое изложение первой нормальной формы
Например, следующая таблица не соответствует 1NF, поскольку сотрудник Tina связан с двумя местоположениями, оба из которых находятся в одной ячейке:
Первая нормальная форма несоответствия
Разрешение такого дизайна может отрицательно повлиять на обновления данных или записи. Чтобы обеспечить соответствие 1NF, переставьте таблицу так, чтобы все атрибуты (или ячейки столбцов) содержали одно значение:
Первая нормальная форма соответствия
Расположение сотрудников Джон Лос-Анджелес Тина Лос-Анджелес Тина Чикаго
Но 1NF все еще недостаточно, чтобы избежать проблем с данными.
Как 2NF работает для обеспечения полной зависимости
Чтобы быть полностью зависимыми, все атрибуты ключа, не являющиеся кандидатами, должны зависеть от первичного ключа. (Помните, что атрибут ключа-кандидата — это любой ключ (например, первичный или внешний ключ), используемый для уникальной идентификации записи в базе данных.
Разработчики базы данных используют нотацию для описания зависимых отношений между атрибутами:
Отделы персонала
EmployeeID
DeptID
Чтобы эта таблица соответствовала 2NF, нам нужно разделить данные на две таблицы:
Сотрудники
Мы удаляем атрибут DeptName из таблицы Employees и создаем новую таблицу Departments :
ведомства
Теперь отношения между таблицами полностью зависимы или в 2NF.
Почему важна полная зависимость
Полная зависимость между атрибутами базы данных помогает обеспечить целостность данных и избежать аномалий данных.
Например, рассмотрим таблицу в разделе выше, которая придерживается только 1NF. Вот и снова:
Первая нормальная форма соответствия
Сотрудник
У Тины две записи. Если мы обновим один, не осознавая, что их два, результатом будут противоречивые данные.
Или, что если мы хотим добавить сотрудника в эту таблицу, но мы еще не знаем местоположение? Возможно, мы не сможем даже добавить нового сотрудника, если атрибут Location не допускает значения NULL.
Однако полная зависимость — это не вся картина, когда дело доходит до нормализации. Вы должны убедиться, что ваша база данных находится в третьей нормальной форме (3NF).
Функциональные зависимости, замыкание множества функциональных зависимостей, атрибутов.
Содержание
Функциональные зависимости
| $A_1$ | $A_2$ | $A_3$ | $A_4$ | |
|---|---|---|---|---|
| $R$ | фирма X | улица Ленина, д.1 | сахар | 40 |
| фирма X | улица Ленина, д.1 | карамель | 50 | |
| фирма X | улица Ленина, д.2 | пастила | 90 |
А первая ФЗ (1) не имеет место быть (в третьей строке другой номер дома портит всю картину).
Замыкание множества функциональных зависимостей
Аксиомы Армстронга
Или правила вывода функциональной зависимости. Существуют различные интерпретации аксиом, но все эквивалентны. Потому приведём только один вариант.
Аксиомы Армстронга являются надёжными и полными.
Рефлексивность
Дополнение
Транзитивность
Пример построения множества ФЗ
Лемма
Справедливы следующие правила. Для их доказательства необходимо пополнить ФЗ так, чтобы можно было использовать аксиомы.
Правило объединения
Правило декомпозиции
Правило псевдотранзитивности
Замыкание множества атрибутов
$X\rightarrow Y \subseteq F^+$
Для этого применяется замыкание множества атрибутов.
Алгоритм построения
Алгоритм является итерационной процедурой.
Пример построения
$F=(AB\rightarrow C, C\rightarrow A, BC\rightarrow D, ACD\rightarrow B, D\rightarrow EG, BE\rightarrow C, CG\rightarrow BD, CE\rightarrow AG)$
Базы данных. Вводный курс
7.2. Функциональные зависимости
Наиболее важные с практической точки зрения нормальные формы отношений основываются на фундаментальном в теории реляционных баз данных понятии функциональной зависимости. Для дальнейшего изложения нам потребуется несколько определений и утверждений (по ходу изложения мы будем пояснять их и иллюстрировать).
7.2.1. Общие определения
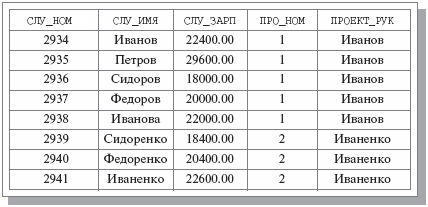
На самом деле, для тела отношения СЛУЖАЩИЕ_ПРОЕКТЫ в том виде, в котором оно показано на рис. 7.1, выполняются еще и следующие FD (1):
Рис. 7.1. Пример возможного тела отношения СЛУЖАЩИЕ_ПРОЕКТЫ
Поскольку имена всех служащих различны, то выполняются и такие FD (2):
Более того, для примера на рис. 7.1 выполняется и FD (3):
Однако заметим, что природа FD группы (1) отличается от природы FD групп (2) и (3). Логично предположить, что идентификационные номера служащих должны быть всегда различны, а у каждого проекта имеется только один руководитель. Поэтому FD группы (1) должны быть верны для любого допустимого значения переменной отношения СЛУЖАЩИЕ_ПРОЕКТЫ и могут рассматриваться как инварианты, или ограничения целостности этой переменной отношения.
Наконец, FD группы (3) основана на совсем неестественном предположении, что никакие двое служащих, участвующие в разных проектах, не получают одинаковую зарплату. Опять же, данное предположение верно для примера из рис. 7.1, но, скорее всего, это случайное совпадение.
В дальнейшем нас будут интересовать только те функциональные зависимости, которые должны выполняться для всех возможных значений переменных отношений.
Заметим, что если атрибут A отношения R является возможным ключом, то для любого атрибута B этого отношения всегда выполняется FD A

Итак, мы будем иметь дело с FD, которые выполняются для всех возможных состояний тела соответствующего отношения и могут рассматриваться как ограничения целостности. Как показывает (неполный) список (1), таких зависимостей может быть очень много. Поскольку они трактуются как ограничения целостности, за их соблюдением должна следить СУБД. Поэтому важно уметь сократить набор FD до минимума, поддержка которого гарантирует выполнение всех зависимостей. Мы займемся этим в следующих подразделах.
FD A

Поскольку тривиальные FD выполняются всегда, их нельзя трактовать как ограничения целостности, и поэтому они не представляют интереса с практической точки зрения. Однако в теоретических рассуждениях их наличие необходимо учитывать.
7.2.2. Замыкание множества функциональных зависимостей. Аксиомы Армстронга. Замыкание множества атрибутов
Истинность первой аксиомы Армстронга следует из того, что при B

Алгоритм вычисления Z + очень прост. Один из его вариантов показан на рис. 7.2.
Рис. 7.2. Алгоритм построения замыкания атрибутов над заданным множеством FD
28 К сожалению, классическая статья Армстронга – W.W. Armstrong. «Dependency Structures of Data Base Relationships», Proc. IFIP Congress, Stockholm, Sweden, 1974 – так и не переведена на русский язык (на самом деле, ее нелегко найти и в оригинале). Поэтому я не могу рекомендовать ее для дополнительного чтения, хотя обязан сослаться.
29 Мы используем здесь знаки операций проверки включения множеств, что не совсем корректно, поскольку если, например, множество B состоит из одного элемента, то для его обозначения используется имя соответствующего атрибута, и в этом случае правильнее было бы использовать знак «