Что такое векторные диаграммы и для чего они нужны

Применение векторных диаграмм при расчете и исследовании электрических цепей переменного тока позволяет наглядно представлять рассматриваемые процессы и упрощать производимые электротехнические расчеты.

При расчете цепей переменного тока часто приходится суммировать (или вычитать) несколько однородных синусоидально изменяющихся величин одной и той же частоты, но имеющих разные амплитуды и начальные фазы. Такую задачу можно решать аналитическим путем тригонометрических преобразований или геометрически. Геометрический метод более прост и нагляден, чем аналитический.

Векторные диаграммы являются совокупностью векторов, изображающих действующие синусоидальные ЭДС и токи или их амплитудные значения.

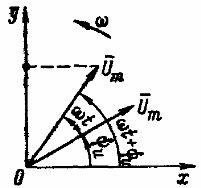
Гармонически изменяющееся напряжение определяется выражением u = U_m sin ( ωt + ψ _и ).

Рис. 1. Изображение синусоидального напряжения вращающегося вектора

При расчете цепи переменного тока часто приходится складывать ЭДС, токи или напряжения одной и той же частоты.

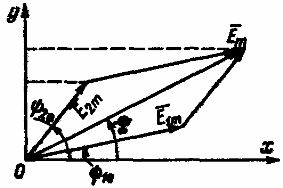
Такое сложение можно осуществить аналитически и графически. Последний способ более нагляден и прост. Две складываемые ЭДС е₁ и е₂ в определенном масштабе представлены векторами E_{1 m} E _2m (рис. 2). При вращении этих векторов с одной и той же частотой вращения, равной угловой частоте, взаимное расположение вращающихся векторов остается неизменным.

Рис. 2. Графическое сложение двух синусоидальных ЭДС одинаковой частоты

Сумма проекций вращающихся векторов E_{1 m} и E _2m на ось ординат равна проекции на ту же ось вектора E m, являющегося их геометрической суммой. Следовательно, при сложения двух синусоидальных ЭДС одной и той же частоты получается синусоидальная ЭДС той же частоты, амплитуда которой изображается вектором E _m, равным геометрической сумме векторов E_{1 m} и E _2m: E _m = E_{1 m} + E _2m.

Векторы переменных ЭДС и токов являются графическими изображениями ЭДС и токов в отличие от векторов физических величин, имеющих определенное физическое значение: вектора силы, напряженности поля и других.

Указанный способ можно применить для сложения и вычитания любого числа ЭДС и токов одной частоты. Вычитание двух синусоидальных величин можно представить в виде сложения: e₁— e₂ = e₁+ (- e₂), т. е. уменьшаемая величина складывается с вычитаемой, взятой с обратным знаком. Обычно векторные диаграммы строятся не для амплитудных значений переменных ЭДС и токов, а для действующих величин, пропорциональных амплитудным значениям, так как все расчеты цепей обычно выполняются для действующих ЭДС и токов.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Онлайн журнал электрика

Статьи по электроремонту и электромонтажу

Что такое векторные диаграммы и для чего они нужны

Применение векторных диаграмм при расчете и исследовании электронных цепей переменного тока позволяет наглядно представлять рассматриваемые процессы и упрощать производимые электротехнические расчеты.

Векторные диаграммы являются совокупой векторов, изображающих действующие синусоидальные ЭДС и токи либо их амплитудные значения.

Гармонически изменяющееся напряжение определяется выражением u = U_m sin ( ωt + ψ _и ).

Рис. 1. Изображение синусоидального напряжения вращающегося вектора

Если, к примеру, исходный фазовый угол напряжения ψ и больше исходного фазового угла ψi то сдвиг по фазе φ = ψ _и — ψ_i и этот угол откладывается в положительном направлении от вектора тока.

При расчете цепи переменного тока нередко приходится ложить ЭДС, токи либо напряжения одной и той же частоты.

Такое сложение можно выполнить аналитически и графически. Последний метод более нагляден и прост. Две складываемые ЭДС е₁ и е₂ в определенном масштабе представлены векторами E_{1 m} E _2m (рис. 2). При вращении этих векторов с одной и той же частотой вращения, равной угловой частоте, обоюдное размещение крутящихся векторов остается постоянным.

Рис. 2. Графическое сложение 2-ух синусоидальных ЭДС схожей частоты

Сумма проекций крутящихся векторов E_{1 m} и E _2m на ось ординат равна проекции на ту же ось вектора E m, являющегося их геометрической суммой. Как следует, при сложения 2-ух синусоидальных ЭДС одной и той же частоты выходит синусоидальная ЭДС той же частоты, амплитуда которой изображается вектором E _m, равным геометрической сумме векторов E_{1 m} и E _2m: E _m = E_{1 m} + E _2m.

Векторы переменных ЭДС и токов являются графическими изображениями ЭДС и токов в отличие от векторов физических величин, имеющих определенное физическое значение: вектора силы, напряженности поля и других.

Обозначенный метод можно применить для сложения и вычитания хоть какого числа ЭДС и токов одной частоты. Вычитание 2-ух синусоидальных величин можно представить в виде сложения: e₁— e₂ = e₁+ (- e₂), т. е. уменьшаемая величина складывается с вычитаемой, взятой с оборотным знаком. Обычно векторные диаграммы строятся не для амплитудных значений переменных ЭДС и токов, а для действующих величин, пропорциональных амплитудным значениям, потому что все расчеты цепей обычно производятся для действующих ЭДС и токов.

Источник

Векторная диаграмма для трехфазной цепи

Цепь трехфазного тока может содержать в себе различные компоненты. Для ее стабильной работы, необходимо правильно рассчитать все напряжения, нагрузки и иные параметры. Статья даст подробное описание, что такое векторная диаграмма для трехфазной цепи, опишет ее разновидности, способы расчета.

Определение

Векторной диаграммой называют метод графического изображения расчета всех параметров цепи переменного тока в виде векторов. Данный метод предполагает изображение всех составных напряжений, токов и процессов в виде отложенных векторов на плоскости.

Назначение

Векторная диаграмма используется для расчетов напряжений, токов в трехфазной цепи и других цепях переменного тока. Метод помогает определить значение всех процессов, происходящих в схеме, их влияние на каждый проводник, нейтраль, а также провести расчет возникающих нагрузок.

Разновидности

Векторные диаграммы трехфазных сетей могут быть симметричными или несимметричными. Построение гистограммы прямо зависит от ее схемы. Разновидности цепей и их гистограмм описаны далее в статье.

Симметричные

Симметричные цепи переменного тока предполагают соединение 3 фаз от источника (генератора) с тремя приемниками.

При этом создаются совершенно независимые трехфазные схемы. При этом используется соединение трех фаз генератора звездой. Для симметричных схем должны соблюдаться требования:

Также учитывается принцип чередования ЭДС во времени. Если ротор генератора вращается по часовой стрелке (правое вращение), то происходит чередование прямого типа (A, B, C). Такая система считается симметричной.

Если ротор вращается против часовой стрелки (левое вращение), чередование считается обратным (A, C, B), но общая система ЭДС остается все так же симметричной.

Для симметричных схем применяется расчет по векторной гистограмме, приведенной ниже.

Несимметричные

Несимметричные цепи предполагают разницу сопротивлений на каждой фазе. Подобная разница может возникнуть при возникновении обрыва одного проводника или нейтрали, его плохого контакта, короткого замыкания. Например, при обрыве нейтрального провода возникает:

При расчете несимметричной цепи также берется расчет соединения источника с приемниками по схеме звезда. Разница состоит в дополнительном расчете смещений, сдвигов фаз и величин сопротивления каждого проводника.

Ниже приведена векторная диаграмма несимметричной цепи.

Построение диаграммы

Векторная диаграмма предполагает в своей основе следующие значения:

Данные значения дополняются единицей времени, за которое ток, под определенным напряжением и силой достигает приемников. Исходя из построения получаем результат: UAB=UBC=UCA.

А это значит то, что если фазная система напряжений симметрична, то линейная система также симметрична и равна, а кроме того имеет сдвиг на 120 градусов. Это простое определение вектора трехфазной цепи.

Переменный ток представляет собой синусоиду, которая может быть графически наложена на ось координат. При этом вектор имеет угловую скорость вращения, которая равна угловым частотам тока. При построении необходимо также учесть то, что вектор является графическим изображением амплитуды колебания, в котором угол колебания равен начальной точке отсчета.

Например, за ось координаты выбрано значение 0. Также известно значение угла смещения. Далее стоит провести вектор «Im», который определяет направление движения тока. При построении вектора с использованием этих значений станут видны параметры опережения, отставания или сдвига фазы. Таким образом можно визуально увидеть разницу величин на каждом проводнике схемы.

Заключение

Если вы работаете с трехфазными цепями, то векторная диаграмма используется для получения визуального отображения всех действующих процессов в таких цепях переменного трехфазного тока. Такая диаграмма полезна при определении несоответствий схемы между углами сдвига фаз, напряжениями и токами.

Видео по теме

Источник

Векторная диаграмма токов и напряжений

Процессы, протекающие в электроцепи переменного тока с активным сопротивлением и реактивной индуктивностью, можно наглядно выразить в графическом виде.

Статья даст описание, что такое векторные диаграммы, где и для чего они используются. Также будет описана временная диаграмма и ее назначение. В конце будет дан пример построения простой диаграммы для электроцепи с последовательным соединением элементов.

Определение

Векторная диаграмма токов и напряжений — это геометрическое изображение всех процессов, величин и амплитуд синусоидального тока. Все имеющиеся величины располагаются на плоскости в виде векторов.

Построение векторной диаграммы использует физика и электротехника. Благодаря созданию такой диаграммы можно значительно упростить выполняемые расчеты, а так же в наглядном и доступном виде отобразить происходящие процессы.

Метод векторных диаграмм позволяет также увидеть в цепи переменного тока возникающие короткие и межфазовые замыкания, а также вычислить возможные потери мощности.

Обычно такая диаграмма строится вместе с временной. Временная диаграмма — это графическое изображение входа и выхода в электрической цепи. Временные диаграммы помогают определить временной промежуток между началом, протеканием и окончанием сигнала. Например, при нажатии на кнопку возникает сигнал, который поступает к приемнику и запускает процесс его работы.

Временные диаграммы также применимы к синусоидальной электрической цепи, так как этот ток имеет начальную точку отсчета (включение питания) и время движения от источника тока к потребителю. Такие диаграммы представляют собой график, на котором изображается начальная точка отсчета, вектор времени и углы смещения фаз.

Разновидности

Разобравшись, что такое и для чего применяется векторная диаграмма, нужно узнать какие разновидности построения существуют. Они отличаются по характеру построения и типу. По характеру бывают:

Векторную диаграмму токов можно построить 2 разными способами:

Оба построения могут использоваться для расчета характеристик переменного тока в цепи с сопротивлением и индуктивностью.

Построение

Построение простых векторных диаграмм будет рассмотрено в данном разделе. Для примера можно взять простую цепь с несколькими элементами и их значениями. Такая схема подразумевает последовательное соединение элементов между собой. Цепь состоит из катушки индуктивности, конденсатора и активного сопротивления. Параметры каждого элемента цепи приведены ниже.

Далее можно сделать простую диаграмму, которая поможет определить напряжение для всей схемы.

Поэтому если есть схема с последовательным соединением элементов, то всегда можно довольно просто построить векторную диаграмму и рассчитать общее напряжение для такой схемы.

Способ 2

Построение векторных диаграмм с учетом всех известных значений для цепи переменного тока с последовательным соединением конденсатора, резистора и катушки индуктивности. При таком построении нам так же известно напряжение самой цепи. Цепь состоит из:

Данная диаграмма может использоваться для контроля и расчета влияния всех известных параметров цепи и элементов, а также их взаимосвязи между собой.

Основное преимущество векторной диаграммы заключается в следующем — простое и быстрое сложение, вычитание двух параметров во время расчета электрических цепей.

Понятие о векторах и векторных диаграммах также подразумевает расчет цепи питания трехфазной сети, подключенной по методу звезды. Она строится с учетом сразу 3 отложенных векторов от 0 оси ординат. Такое построение определяет вектор от источника тока к приемнику. Строится вектор со следующими значениями:

Далее нужно сделать:

Таким же образом на плоскость накладываются еще две прямые линии. Общая диаграмма покажет симметричность фаз или их сдвиг при появлении короткого замыкания. Такая диаграмма может стать примером для расчета напряжения, тока или нагрузки на каждую фазу с моделированием различных параметров.

Заключение

Векторные диаграммы сложны в понимании при расчете сложных цепей, с большим количеством сопротивлений и индуктивностью. Также, при расчете стоит учитывать тип соединения всех элементов, симметрию цепи и основные ее значения.

Видео по теме

Источник

Векторные диаграммы

Векторные диаграммы и комплексное представление

Тогда вектор длиной A, вращающийся в комплексной плоскости с постоянной угловой скоростью ω с начальным углом φ₀ запишется как комплексное число

а его действительная часть

-есть гармоническое колебание с циклической частотой ω и начальной фазой φ₀.

Хотя, как видно уже из вышесказанного, векторные диаграммы и комплексное представление колебаний теснейшим образом связаны и по сути представляют собой варианты или разные стороны одного и того же метода, они, тем не менее, обладают своими особенностями и могут применяться и по отдельности.

Разновидности векторных диаграмм

Для корректного отображения переменных величин, которые определяют функциональность радиотехнических устройств, хорошо подходит векторная графика. Подразумевается соответствующее изменение основных параметров сигнала по стандартной синусоидальной (косинусоидальной) кривой. Для наглядного представления процесса гармоническое колебание представляют, как проекцию вектора на координатную ось.

С применением типовых формул несложно рассчитать длину, которая получится равной амплитуде в определенный момент времени. Угол наклона будет показывать фазу. Суммарные влияния и соответствующие изменения векторов подчиняются обычным правилам геометрии.

Различают качественные и точные диаграммы. Первые применяют для учета взаимных связей. Они помогают сделать предварительную оценку либо используются для полноценной замены вычислений. Другие создают с учетом полученных результатов, которые определяют размеры и направленность отдельных векторов.

Допустим, что надо изучить изменение параметров тока в цепи при разных значениях сопротивления резистора в диапазоне от нуля до бесконечности. В этой схеме напряжение на выходе (U) будет равно сумме значений (UR и UL) на каждом из элементов. Индуктивный характер второй величины подразумевает перпендикулярное взаимное расположение, что хорошо видно на части рисунка б). Образованные треугольники отлично вписываются в сегмент окружности 180 градусов. Эта кривая соответствует всем возможным точкам, через которые проходит конец вектора UR при соответствующем изменении электрического сопротивления. Вторая диаграмма в) демонстрирует отставание тока по фазе на угол 90°.

Здесь изображен двухполюсный элемент с активной и реактивной составляющими проводимости (G и jB, соответственно). Аналогичными параметрами обладает классический колебательный контур, созданный с применением параллельной схемы. Отмеченные выше параметры можно изобразить векторами, которые расположены постоянно под углом 90°. Изменение реактивной компоненты сопровождается перемещением вектора тока (I1…I3). Образованная линия располагается перпендикулярно U и на расстоянии Ia от нулевой точки оси координат.

Механика; гармонический осциллятор

Разберем два основных случая простого применения векторных диаграмм в механике (как замечено выше, также применимых к гармоническому осциллятору не только механической, но любой природы): осциллятор без затухания и без внешней силы и осциллятор с (линейным) затуханием (вязкостью), и внешней вынуждающей силой.

Представление синусоидальных функций в виде комплексных чисел

Векторная диаграмма – это удобный инструмент представления синусоидальных функций времени, коими являются, к примеру, напряжения и токи электрической цепи переменного тока.

Рассмотрим, например, произвольный ток, представленный в виде синусоидальной функции

Данный синусоидальный сигнал можно представить в виде комплексной величины

Для формирования комплексного числа используются модуль и фаза синусоидального сигнала.

Векторная диаграмма при последовательном соединении элементов

Для построения векторных диаграмм сперва составляют уравнения по законам Кирхгофа для рассматриваемой электрической цепи.

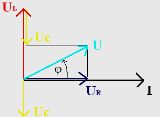
Рассмотрим электрическую цепь, представленную на рис. 1, и нарисуем для неё векторную диаграмму напряжений. Обозначим падение напряжение на элементах.

Рис. 1. Последовательное соединение элементов цепи

Составим уравнение для данной цепи по второму закону Кирхгофа :

По закону Ома падение напряжений на элементах определяется по следующим выражениям:

Для построения векторной диаграммы необходимо отобразить приведённые в уравнении слагаемые на комплексной плоскости. Обычно вектора токов и напряжений отображаются в своих масштабах: отдельно для напряжений и отдельно для токов.

Из курса математики известно, что j = 1∠90°, −j = 1∠−90°. Отсюда при построении векторной диаграммы умножение какого-либо вектора на мнимую единицу j приводит к повороту этого вектора на 90 градусов против часовой стрелки, а умножение на −j приводит к повороту этого вектора на 90 градусов по часовой стрелке.

При построении векторной диаграммы напряжений на комплексной плоскости сперва отобразим вектор тока I, после чего относительного него будем отображать вектора падений напряжений (рис. 2) с учётом приведённых выше соотношений для мнимой единицы.

Падение напряжения на резисторе U_R совпадает по направлению с током I (т.к. U_R = I ∙ R, а R – чисто действительная величина или, простыми словами, нет умножения на мнимую единицу). Падение напряжения на индуктивном сопротивлении опережает вектор тока на 90° (т.к. U_L = I ∙ jX_L, а умножение на j приводит повороту этого вектора на 90° против часовой стрелки). Падение напряжения на ёмкостном сопротивлении отстаёт от вектора тока на 90° (т.к. U_C = −I ∙ jX_C, а умножение на −j приводит повороту этого вектора на 90° по часовой стрелке).

Рис. 2. Векторная диаграмма напряжений при последовательном соединении элементов цепи

Векторная диаграмма при параллельном соединении элементов

Рассмотрим электрическую цепь, представленную на рис. 3, и нарисуем для неё векторную диаграмму токов. Обозначим направление токов в ветвях.

Рис. 3. Параллельное соединение элементов цепи

Составим уравнение для данной цепи по первому закону Кирхгофа :

Определим по закону Ома токи в ветвях по следующим выражениям, учитывая, что 1 / j = −j:

Для построения векторной диаграммы необходимо отобразить приведённые в уравнении слагаемые на комплексной плоскости.

При построении векторной диаграммы токов на комплексной плоскости сперва отобразим вектор ЭДС E, после чего относительного него будем отображать вектора токов токов (рис. 4) с учётом приведённых выше соотношений для мнимой единицы.

Ток в резисторе I_R совпадает по направлению с ЭДС E (т.к. I_R = E / R, а R – чисто действительная величина или, простыми словами, нет умножения на мнимую единицу). Ток в индуктивном сопротивлении отстаёт от вектора ЭДС на 90° (т.к. I_L = −j ∙ E / X_L, а умножение на −j приводит повороту этого вектора на 90° по часовой стрелки). Ток в ёмкостном сопротивлении опережает вектор ЭДС на 90° (т.к. I_C = j ∙ E / X_C, а умножение на j приводит повороту этого вектора на 90° против часовой стрелки). Результирующий вектор тока определяется после геометрического сложения всех векторов по правилу параллелограмма.

Рис. 4. Векторная диаграмма токов при параллельном соединении элементов цепи

Для произвольной цепи алгоритм построения векторных диаграмм аналогичен вышеизложенному с учётом протекаемых в ветвях токов и прикладываемых напряжений.

Обращаем ваше внимание, что на сайте представлен инструмент для построения векторных диаграмм онлайн для трёхфазных цепей.

Алгоритм создания лучевой векторной диаграммы в Excel

Чтобы упростить наш урок, давайте предположим, что мы говорим об отношениях не между четырнадцатью как на графике, а пока только с 4-ма людьми по имени Антон, Алиса, Борис и Белла.

Наша матрица уровня отношений и связей между ними выглядит следующим образом:

Как можно геометрически смоделировать визуализацию этих исходных данных? Если бы мы нарисовали отношения между этими четырьмя людьми (Антон, Алиса, Борис и Белла), это схематически выглядело бы так:

2 критерия, которые нам нужно определить:

Определение и построение точек

Сначала нам нужно построить наши точки таким образом, чтобы промежуток между каждой точкой был одинаковым. Это создаст сбалансированный график.

Какая геометрическая фигура максимально удовлетворяет нашу потребность в таких равных промежутках? Конечно же круг!

Вы можете возразить, что на готовой модели диаграммы нет фигуры круга. Да действительно нет –вот так. Нам не нужно рисовать круг. Нам просто нужно построить точки вокруг него.

Таким образом, у нас есть 4 заинтересованные стороны, нам нужно 4 точки:

Предполагая, что источником нашего круга является (x, y), радиус – это r, а тета – 360, деленная на количество нужных нам точек. Первая точка (x1, y1) на окружности будет в этой позиции:

Как только все точки рассчитаны и подключены к XY-диаграмме (точечная диаграмма), давайте двигаться дальше.

Построение линий на лучевой диаграмме

Нам нужно разделить его на 2, как будто A знает B, тогда B тоже знает A. Но нам нужно нарисовать только 1 линию.

Шаблон лучевой диаграммы для анализа сетевого графика настроен для работы с 20 людьми. Его можно скачать в конце статьи и использовать как готовый аналитический инструмент визуализации данных связей. Это означает, что максимальное количество строк, которое мы можем иметь, будет равно 190.

Каждая строка требует добавления отдельной серии на график. Это означает, что нам нужно добавить 190 серий данных только для 20 человек. И это удовлетворяет только одному типу линии (пунктирная или толстая). Если нам нужны разные линии в зависимости от типа отношений, нам нужно добавить еще 190 серий.

Это больно и смешно одновременно. К счастью, выход есть!

Мы можем использовать гораздо меньшее количество серий и по-прежнему строить один и тот же график.

Допустим, у нас есть 4 человека – A,B,C и D. Ради простоты, давайте предположим, что координаты этих 4-х участников следующие:

И скажем, A имеет отношения с B, C и D.

Это означает, что нам нужно нарисовать 3 линии, от A до B, от A до C и A до D.

Теперь, вместо того, чтобы поставить 3 серии для диаграммы, что если мы поставим одну длинную серию, которая выглядит следующим образом:

Это означает, что мы просто рисуем одну длинную линию от A до B, от A до C, от A до D. Договорились, что это не прямая линия, но точечные диаграммы Excel могут нарисовать любую линию, если вы предоставите ей набор координат.

Смотрите эту иллюстрацию, чтобы понять технику:

Таким образом, вместо 190 рядов данных для диаграммы нам просто нужно 20 рядов.

На последнем графике мы имеем 40 + 2 + 1 ряд данных. Это потому что:

Как сгенерировать все 20 серий данных:

Это требует следующей логики:

Нам нужны формулы MOD и INDEX для выражения этой логики в Excel.

Как только все координаты линии будут рассчитаны, добавьте их к нашему точечному графику как новые ряды используя инструмент из дополнительного меню: «РАБОТА С ДИАГРАММАМИ»-«КОНСТРУКТОР»-«Выбрать данные» в окне «Выбор источника данных» используйте кнопку «Добавить» для добавления всех 43-х рядов.

Реализовывать создание такой лучевой диаграммы связей будем в 3 этапа:

Подготовка данных для лучевой диаграммы

Как уже упоминалось выше данный шаблон будет обладать возможностью визуального построения связей до 20-ти участников (компаний, филиалов, контрагентов и т.п.). На листе книги шаблона «Данные» предоставленная таблица для заполнения входящих значений. Например, заполним ее для 14-ти участников рынка:

На этом же листе создадим дополнительную таблицу, которая представляет собой матрицу связей всех возможных участников, сгенерированную формулой:

С подготовкой данных мы закончили переходим к обработке.

Как вычислить сумму векторов?

Вектора и матрицы в электронной таблице хранятся в виде массивов.

Известно, что сумма векторов – это вектор, координаты которого равны суммам соответствующих координат исходных векторов:

Для вычисления суммы векторов нужно выполнить следующую последовательность действий:

– В диапазоны ячеек одинаковой размерности ввести значения числовых элементов каждого вектора.

– Выделить диапазон ячеек для вычисляемого результата такой же размерности, что и исходные векторы.

– Ввести в выделенный диапазон формулу перемножения диапазонов

– Нажать комбинацию клавиш [Ctrl] + [Shift] +[Enter].

Требуется вычислить сумму этих векторов.

– В ячейки диапазона А2:A4 введем значения координат вектора a1, а в ячейки диапазона С2:С4 – координаты вектора a2.

– Выделим ячейки диапазона, в которых будет вычисляться результирующий вектор С ( E2:E4 ) и введем в выделенный диапазон формулу:

– Нажмем комбинацию клавиш [Ctrl] + [Shift] +[Enter]. В ячейках диапазона E2:E4 будут вычислены соответствующие координаты результирующего вектора.

Сложение и вычитание векторов

Главным достоинством векторных — это возможность простого сложения и вычитания двух величин. Например: требуется сложить, два тока, заданных уравнениями

Сложим два заданных тока i1 и i2 по известному правилу сложения векторов (рис. 12.12, а). Для этого изобразим токи в виде векторов из общего начала 0. Результирующий вектор найдем как диагональ параллелограмма, построенного на слагаемых векторах:

Сложение векторов, особенно трех и более, удобнее вести в таком порядке: один вектор остается на месте, другие переносятся параллель
но самим себе так, чтобы начало последующего вектора совпало с концом предыдущего.

Вектор I_m, проведенный из начала первого вектора в конец последнего, представляет собой сумму всех векторов (рис. 12.12, б).

Вычитание одного вектора из другого выполняют сложением прямого вектора (уменьшаемого) и обратного (вычитаемого) (рис. 12.13):

При сложении синусоидальных величин в отдельных случаях можно применить аналитическое решение: применительно к рис. 12.12, а — по теореме косинусов; к рис. 12.14, а — сложение модулей векторов; б — вычитание модулей векторов, в — по теореме Пифагора.

Источник